Лаб практикум по СТУ 2009

гдеW ′(z) не содержит полюсов z = 1. Объединив звенья W(z) и D(z), получим

окончательное выражение для регулятора цифровой системы в виде

W (z)

z

m

(z −1)

m−1

′

Wp (z) =

=

W (z)Q1(z)

. (18)

1+W (z)D(z)

z

m

(z −1)

i+ j−1

′

m−1

Q1(z) +W (z)P(z)(z

+ ...+ z +1)

Анализ ДПФ регулятора (18) позволяет сделать два важных вывода:

1)знаменатель (18) не содержит сомножителя (z-1) даже при j ≥ 1, что подтверждает известный вывод, что при таком способе компенсации запаздывания порядок астатизма системы на рис. 10 определяется количеством интеграторов объекта и практически отсутствует возможность изменить его за счет регулятора;

2)регулятор (18) компенсирует полином Q1(z) объекта, т.е. его полюсы, даже если это не предполагалось при синтезе регулятора W(z).

Очевидно, что такой регулятор неприменим в системах с высокими требованиями к статическим характеристикам, а также для неустойчивых объектов, так как в этом случае компенсация неустойчивых полюсов объекта делает систему негрубой.

Рассмотрим теперь процедуру синтеза методом полиномиальных уравнений для объекта (16), считая в общем случае, что ДПФ объекта содержит как устойчивые, так и неустойчивые нули и полюсы. Выполним факторизацию ДПФ объекта, представив полиномы знаменателя и числителя (16) в виде

Q(z) = Qк(z)Qн(z); P(z) = Pк (z)Pн (z) ,

где Qк(z), Pк(z) и Qн(z), Pн(z) – полиномы от z степени nQк, nPк и nQн, nPн соответственно, содержащие компенсируемые и некомпенсируемые полюсы и нули объекта.

Cинтезируемая система будет оставаться устойчивой при малых изменениях параметров объекта («грубой»), если регулятор не компенсирует неустойчивые нули и полюсы объекта, поэтому все неустойчивые нули и полюсы должны быть отнесены к некомпенсируемой части объекта. Кроме того, известно, что компенсация устойчивых нулей объекта в цифровых системах приводит к возникновению скрытых колебаний координат, а

21

компенсация устойчивых полюсов – к повышенной чувствительности к изменению параметров, но система при этом работоспособна. Поэтому Qк(z) и

Pк(z) могут содержать только устойчивые полюсы и нули объекта, а Qн(z) и

Pн(z) – все неустойчивые и некоторые устойчивые полюсы и нули. Окончательно ДПФ цифрового регулятора компенсационного типа запишем следующим образом:

Wp (z) =	M (z)Qк(z)	,	(19)
	N(z)P (z)(z −1) j
	к

где M(z) и N(z) – искомые полиномы степени nM и nN соответственно; j – количество интегрирующих звеньев регулятора, обеспечивающих требуемый порядок астатизма i+j замкнутой системы. Из условия физической реализуемости степени искомых полиномов должны удовлетворять равенству

nM + nQк = nN + nPк + j .

(20)

Очевидно, что, положив Qк(z) = Pк (z) = 1, из (19) можно получить, как частный случай, ДПФ некомпенсационного регулятора.

Основой для синтеза служит ДПФ замкнутой системы по ошибке:

	1		(z−1)i+ j N (z)Q (z)
Φε(z)=		=		н	,
	1+G(z)		(z−1)i+ j N (z)Q (z)+P (z)M (z)
			н	н

где G(z)=Wp(z)Wo(z). Степень сомножителя (z – 1) в числителе этой ДПФ определяет желаемый порядок астатизма системы по управляющему воздействию, при этом имеется свобода выбора j. Приравняв знаменатель передаточной функции к желаемому характеристическому полиному замкнутой системы A(z), получим следующее полиномиальное уравнение синтеза:

(z −1)i+ j N(z)Q (z) + P (z)M (z) = A(z).		(21)
н	н

Если объект регулирования содержит запаздывание, которое выражается в виде полюсов ДПФ объекта кратности m, равных нулю, целесообразно с целью повышения быстродействия системы отнести сомножитель zm к Qк(z), а

желаемый характеристический полином представить в виде A(z)=zmA1(z). В

22

получаемые при этом регуляторы будут автоматически включены алгоритмы компенсации запаздывания mT.

Выбор степеней полиномов, соответствующих минимальному решению уравнения (21) с учётом условия (20) и обеспечивающих теоретически любое качество регулирования, определяемое A(z), осуществляется по выражениям

nA = 2nQ − nQк + 2i + j −1,

		nN = nQ + i −1,						(22)
	nM = nQ − nQ к + i + j −1.
Задание к работе
1. Задан объект регулирования с передаточной функцией
	Wo	( p) =		ko		,		(23)
				p(To p	+1)
который с учетом экстраполятора нулевого порядка имеет ДПФ вида
	W (z) =		ko( p1z + p0)				,	(24)
	o		(z −1)(z − d)
где р1 = Т – То + dТо;	р0 = То – d(То + Т); d = exp(– T / To).
Для индивидуальных данных, приведенных в лабораторной работе 3 (см.
табл. 6), методом	полиномиальных				уравнений выполнить			синтез

компенсационного (с компенсацией устойчивого полюса объекта) цифрового регулятора, обеспечивающего первый порядок астатизма и показатели качества, соответствующие биномиальному распределению корней характеристического уравнения (табл. 7). Принять период дискретности

Т= 0,1То и Т = 0,5То.

2.Ввести в модель объекта (24) запаздывание на период дискретности Т и

выполнить синтез компенсационного регулятора, компенсирующего устойчивый полюс объекта (т.е. Qк (z) = z − d ), при Т = 0,1То и Т = 0,5То.

3. Для объекта с запаздыванием, полученного в п. 2, выполнить синтез компенсационного регулятора, компенсирующего устойчивый полюс объекта и влияние этого запаздывания (т.е. Qк (z) = z(z − d) ), при Т = 0,1То и Т = 0,5То.

23

4. Выполнить моделирование замкнутой системы с полученными регуляторами при единичном ступенчатом воздействии и измерить показатели качества. При необходимости для устранения перерегулирования использовать на входе замкнутой системы фильтр с ДПФ Wф(z) = M (1) / M (z) . Результаты

измерений свести в таблицу.

5. Сделать выводы о работоспособности полученных цифровых систем и влиянии метода синтеза и периода дискретности на качество регулирования.

		Таблица 7
nA	Характеристический полином	Коэффициенты полинома при
	A(z)	биномиальном распределении корней
1	z – a0	a0 = e-ΩΤ
2	z2 – a1z + a0	a0 = e-2ΩΤ; a1 = 2e-ΩΤ
3	z3 – a2z2 + a1z – a0	a0 = e-3ΩΤ; a1 = 3e-2ΩΤ; a2 = 3e-ΩΤ
4	z4 – a3z3 + a2z2 – a1z + a0	a0 = e-4ΩΤ; a1 = 4e-3ΩΤ; a2 = 6e-2ΩΤ; a3 = 4e-ΩΤ
5	z5 – a4z4 + a3z3 – a2z2 + a1z – a0	a0 = e-5ΩΤ; a1 = 5e-4ΩΤ; a2 = 10e-3ΩΤ;
		a3 = 10e-2ΩΤ; a4 = 5e-ΩΤ

Содержание отчета

1.Название и цель работы, индивидуальные данные.

2.Результаты синтеза регуляторов.

3.Схемы моделирования.

4.Таблица с результатами измерения показателей качества для различных вариантов синтеза и значений периода дискретности.

5.Выводы по работе.

24

Лабораторная работа 5 ИССЛЕДОВАНИЕ МЕТОДИКИ СИНТЕЗА МОДАЛЬНОГО РЕГУЛЯТОРА

Цель работы: изучение методики синтеза модального регулятора.

Краткие теоретические сведения

При анализе и синтезе систем в пространстве состояний все переменные, характеризующие систему или имеющие к ней прямое отношение, делятся на входные переменные, представляющие собой управляющие или

возмущающие воздействия ui, выходные переменные yi, представляющие интерес для исследователя, и промежуточные переменные xi или переменные состояния, определяющие динамическое поведение исследуемой системы.

В основе этой формы математического описания лежит представление дифференциальных уравнений в нормальной форме Коши, которое дополняется алгебраическими уравнениями выхода. В векторно-матричной форме эти уравнения записываются следующим образом:

X& (t) = AX(t) + BU(t);

(25)

Y(t) = CX(t) + DU(t),

где A, B, C и D – матрицы коэффициентов размерности (n×n), (n×m), (r×n), (r×m) соответственно; m – число входов; r – число выходов; U(t) – векторфункция управляющих воздействий размерности m; X(t) – вектор-функция переменных состояния размерности n; Y(t) – вектор-функция выходных координат размерности r.

Матрица А характеризует динамические свойства системы, матрицу В называют матрицей управления, она определяет характер воздействия входных переменных U(t) на переменные состояния X(t).

Алгебраическое уравнение связывает выходные переменные Y(t) с переменными состояния X(t) через матрицу связи С. Обычно в системах

25

автоматического управления матрица D = 0, она характеризует непосредственное воздействие входов на выходы.

Рассмотрим линейную систему, записанную в уравнениях переменных состояния:

X& (t) = AX(t) + BU(t);

(26)

Y(t) = CX(t).

Для системы с одним входом и одним выходом переход от ее передаточной функции W(p) к описанию в пространстве состояний осуществляется следующим образом:

1) передаточная функция приводится к виду

b

pn−1 + ... + b p + b

bn−1

p

n−1

+ ...+

b1

p

+

b0

a

n

a

n

a

n

W ( p) =

n−1

1

0

=

;

an pn + an−1pn−1 + ...+ a1p + a0

n

an−1

n−1

a1

a0

p

+

p

+ ... + an

p + an

an

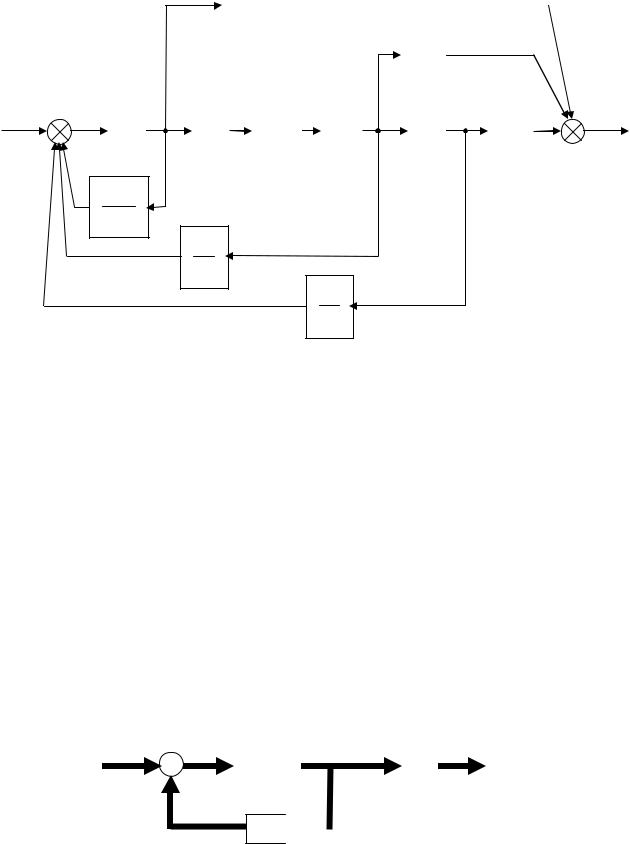
2)после этого ее можно представить в виде структурной схемы рис. 11, которая представляет собой n последовательно соединенных интеграторов;

3)третий этап – это переход от структурной схемы к системе дифференциальных уравнений, по которым составляются матрицы коэффициентов:

	Отсюда
æ	0			1
ç	0			0
ç
A = ç	L		L
ç		a			a
ç	-	0	-		1
ç		an			an
è

	ìx&1 = x2;
	ïx&	2	= x ;
	ï		3
	ï
	íx&n−1 = xn;
	ï			a0
	ïx&	n	= u -		x -
	ï		1
	î			an

y(t) = b0 x1 + b1 an an

a1	x2	-...-	an−1	xn;	(27)
an
			an

x2 + ...+ bn−1 xn. an

0

K

0

ö

æ

0

ö

÷

1

K

0

÷

ç

0

÷

æ b

b

b

ö

ç

÷

÷

ç 0

1

n−1

÷

L

L

;

B = ç

÷ ;

C = ç

K

÷ .

a

an

2

a

n−1

÷

çL÷

è an

an ø

-

K

-

÷

ç

1

÷

an

an

÷

è

ø

ø

26

bn−1

an

b1

u(t)

an

xn(t)

xn-1(t)

x

2(t)

x1(t)

y(t)

1

1

1

1

b0

_

…

p

p

p

p

an

an−1

an

a1

an

a0

an

Рис. 11. Структурная схема объекта, представленная в виде последовательно соединенных интеграторов

Перейдем от дифференциальных уравнений (26) к уравнениям в операторной форме (записанным с помощью оператора Лапласа). Тогда объект можно представить его матричной передаточной функцией

	W( p) =	X( p)	= ( p1 − A)−1B ,	(28)
		U( p)

где 1 – единичная матрица.

Замкнутая система в пространстве состояний показана на рис. 12 и представляет собой систему с параллельной коррекцией, где R – матрица коэффициентов регулятора размерности m×n.

V(t)	U(t)			X(t)		Y(t)
			W(p)		C

R

Рис. 12. Структурная схема замкнутой системы в пространстве состояний

27

	Матричная передаточная функция замкнутой системы
	G( p) =	X( p)	= ( p1 − A + BR)−1B .	(29)
		V( p)

Для синтеза модального регулятора объект, описываемый уравнениями (26), должен быть полностью управляемым и наблюдаемым.

Полная управляемость – это возможность перевода объекта из начального состояния X0 в любое наперед заданное положение X при ограниченном управляющем воздействии.

Критерием полной управляемости по вектору состояния является

равенство	ранга	его	матрицы	управляемости	вида
Qу = (B AB	A2B	L An−1B) порядку системы n:
			rank Qy = n.

Наблюдаемость – возможность по выходному вектору Y(t) определить вектор состояния X(t).

Критерий наблюдаемости: система, описываемая уравнениями (26),

наблюдаема,	если	ранг	ее	матрицы	наблюдаемости	вида
Qн = (Cт AтСт (Aт )2Ст			L (Aт )n−1Ст )равен порядку системы n:

rank Qн = n.

Для объекта с одним входом (m = 1), описываемого системой уравнений (27), модальный регулятор синтезируется следующим образом:

1.Рассматривается система, у которой вектор состояния наблюдаем и совпадает с вектором выхода, т.е. С = 1, тогда Y(t) = X(t).

2.Следует задаться желаемым размещением корней для настройки системы автоматического регулирования. Это может быть биноминальное распределение корней, распределение по Баттерворту, выбор корней по некоторому интегральному показателю качества и т.д.

28

Каждая система, настроенная на определенное размещение корней, характеризуется соответствующим характеристическим полиномом D(p) n-го

	порядка.
	3. Передаточная функция объекта (28) записывается в виде
	W( p) =	H( p)	,	(30)
		F( p)

где F( p) = det( p1 − A) – характеристический полином объекта, а H(p) – вектор-

столбец, состоящий из n элементов, который требуется извлечь из (28).

4. Для того чтобы найти коэффициенты регулятора, необходимо характеристическое уравнение замкнутой системы (вывод формулы опущен)

RH( p) + F( p) = 0

(31)

приравнять к выбранному ранее в п. 2 желаемому стандартному полиному n-го порядка

RH( p) + F( p) = D( p).	(32)
Конечное уравнение имеет вид
RH( p) = D( p) − F( p) ,	(33)

из которого непосредственно находятся коэффициенты вектора-столбца R путем приравнивания коэффициентов, стоящих при одинаковых степенях р в левой и правой частях уравнения соответственно.

Задание к работе

1. Задан объект регулирования с одним входом и одним выходом с передаточной функцией

	W ( p) =				b0			.
		a p3	+ a	2	p2	+ a p + a	0
	3					1

Проверить данный объект на полную управляемость и наблюдаемость. Синтезировать модальный регулятор по предложенной выше методике с настройкой на биноминальное распределение корней замкнутой системы, используя данные:

29

Степень полинома D(p)	Желаемый характеристический
	полином D(p)
1	p + Ω
2	p2 + 2Ωp + Ω2
3	p3 + 3Ωp2 + 3Ω2 p + Ω3
4	p4 + 5Ωp3 +10Ω2 p2 + 5Ω3 p + Ω4

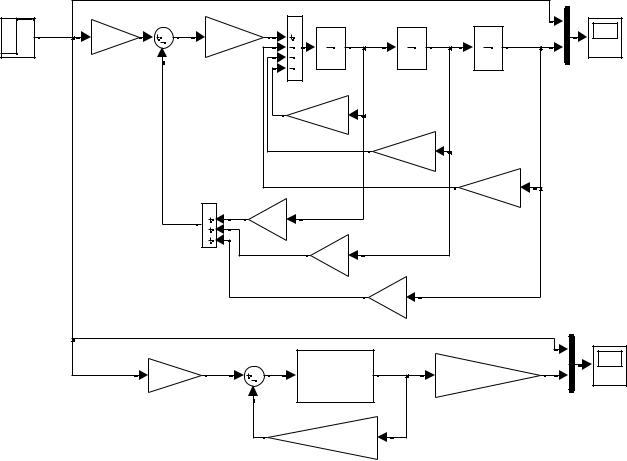
2. Выполнить моделирование замкнутой системы с регулятором при ступенчатом единичном воздействии в двух случаях:

∙собрав структурную схему в развернутом виде в Simulink;

∙собрав структурную схему в матричном виде, используя блок StateSpace и усилительное звено в виде вектора-строки (рис. 13).

3. Сравнить результаты. Сделать выводы о работоспособности системы. Индивидуальные данные по каждому варианту приведены в табл. 8.

	v(t)	u(t)			x3		x2		x1=y(t)
	w^3	b0/a3		1		1		1
Step	Gain	Gain1		s		s		s	Scope
				Integrator		Integrator1
								Integrator2
				a2/a3
				Gain2		a1/a3
						Gain3		a0/a3
			r3					Gain4
			Gain5	r2
				Gain6		r1
						Gain7
		w^3		x' = Ax+Bu			[1 0 0]* u
				y = Cx+Du
									Scope1
		Gain8						Gain9
				State-Space
				[r1 r2 r3]* u
				Gain10

Рис. 13. Схема модели

30