Chast_2_VA_i_AG

1 1 2 6

d 6 .

6

Координаты искомой точки удовлетворяют системе

	x 1			y 1			z 1			,
	1			1			2
															2
			2	y		1		2		z 1	2	2	6
x 1															24,
из которой получаем

x 1 2 x 1 2 4 x 1 2 24 x 1 2 4 x 3, x 1.
1	2
В результате имеем две точки: N1 3,3, 3	и

N2 1, 1,5 . Вторая точка не подходит, так как отстоит от плоскости на 36 .

2) x	xM xN	x	N	3, аналогично	y	N	3, z	N	3
0	2
и N(3,3, 3).

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 3

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ

	1. Прямая на плоскости
№	Задание		Ответ
	Треугольник задан уравнениями трех его сторон:	а)
			А (-1, 2),
	АС: х – 2у + 5 = 0,
		В (9, -3),
	АВ: х + 2у – 3 = 0,
		С (5, 5),
	ВС: 2х + у – 15 = 0.
	Определите следующие элементы треугольника:	б)
	а) координаты вершин.	1						5
		y				x			,
	б) уравнения высот,							2
		2
	в) уравнения медиан,	у=-2х+15,
1	г) длины сторон,	у=2х–5,
		в)
	д) уравнения биссектрис,
		11х–2у–45=0,
	ж) центр и радиус вписанной окружности,
		13х+14у=75,
	з) центр и радиус описанной окружности,	x+8y–15=0,
	и) центр тяжести треугольника,
	к) внутренние углы треугольника,	5
						5,
	л) площадь треугольника.
		г) 4			5,			,
	РЕШЕНИЕ.
		3			5

81

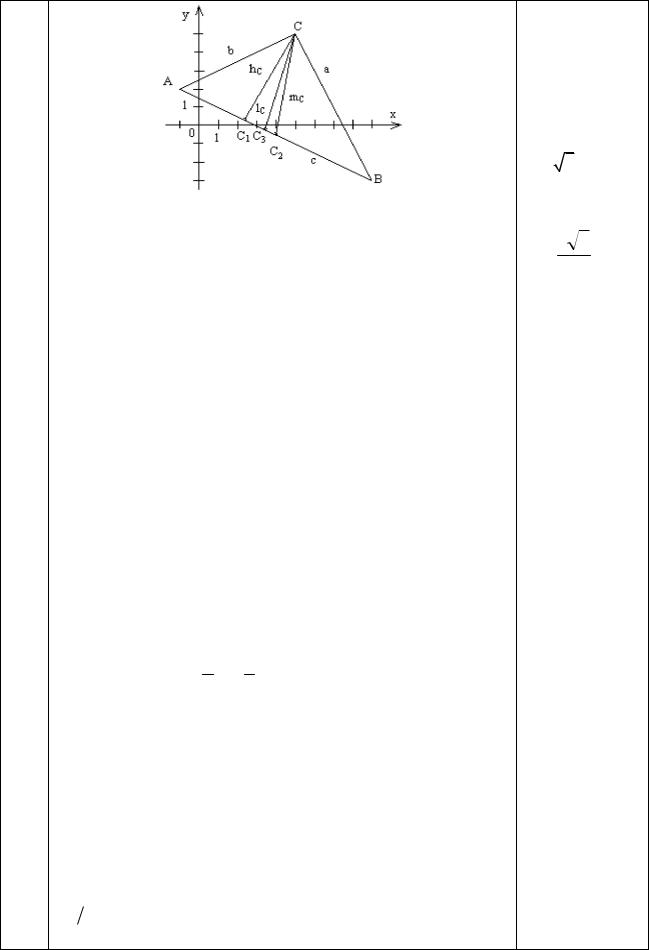
а). Координаты вершин треугольника находятся как точки пересечения соответствующих сторон. Так, например, координаты точки А являются решением системы уравнений

x 2 y 5 0,	А (-1, 2).
x 2y 3 0,

Аналогично находятся В (9, -3) и С (5, 5).

б). Высотой треугольника называется отрезок перпендикуляра, опущенного из вершины треугольника на противоположную сторону.

Уравнение высоты hc = CC1 ищем как уравнение прямой, приходящей через точку С перпендикулярно к

1, 2

AB:

n

AB

и

уравнение

высоты

x 5

y 5

y

1

x

3

.

1

2

2

2

1

5

Анализ уравнений сторон АС: y

x

и

ВС: у = -2х + 5 k1

k2

1

2

2

убеждает в том, что АС

ВС,

треугольник

является

прямоугольным,

значит,

уравнение hA: y 1 x 5 ; hB: у = -2х + 15.

2 2

в). Медианой называется отрезок прямой, соединяющей вершину треугольника с серединой противолежащей стороны.

Координаты середин сторон находятся по формулам деления отрезка в данном отношении: С2 (4, -1/2), В2 (2, 7/2), А2 (7, 1).

Уравнение медианы mC = CC2 получается как уравнение прямой, проходящей через точки С и С2:

	y 5			x	5	или mC: 11х–2у–45=0.
	1 2	5			5
			4
Аналогично						mВ: 13х+14у–75=0,

д)

у = 2, х+у–6=0, 3х–у–10=0,

ж)

О1(4,2), r 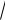5 ,

з)

О2(4,-1/2),

R 5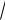5 , 2

и)

	xO	4,35;
	3
	yO	1, 45
	3
	к)			3
	A arccos
				5

л) 30.

82

mА: x+8y–15=0.

г). Длины сторон найдем по формуле расстояния между двумя точками:

AB

c 102 52 5 5,

BC

a 4 5,

AC b 3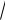5.

д). Биссектрисой треугольника называется лежащий в треугольнике отрезок прямой, которая делит его внутренний угол пополам.

Укажем два способа нахождения уравнения биссектрисы треугольника.

1). Биссектриса делит противолежащую сторону в отношении, пропорциональном прилежащим сторонам.

Если С3 – точка пересечения биссектрисы lC = CC3 со стороной АС, то

АС3 АС b 3. С3 В СВ a 4

Координаты точки С3 находим по формулам деления

отрезка	в	данном	отношении		=	3/4:
С3 (23/7, - 1/7).
Уравнение биссектрисы lC = CC3				получается как
уравнение	прямой, проходящей через точки					С3 и

С (5, 5):
	y 5		x 5		или 3х – у – 10 = 0.
	1 7 5		23 7	5

2). Найдем направляющий вектор биссектрисы

			CA CB							2			1						1			2
lC = CC3: l																		,									.
			CA				CB			5			5						5			5

Таким образом, в качестве направляющего вектора прямой можно взять вектор 1, 3 и уравнение

биссектрисы принимает вид: x 5 y 5 .

1 3

Уравнения lВ: х+у – 6 = 0 и lА: у = 2

могут быть найдены одним из двух способов.

ж). Центр вписанной окружности находится в точке пересечения биссектрис lС и lА треугольника.

83

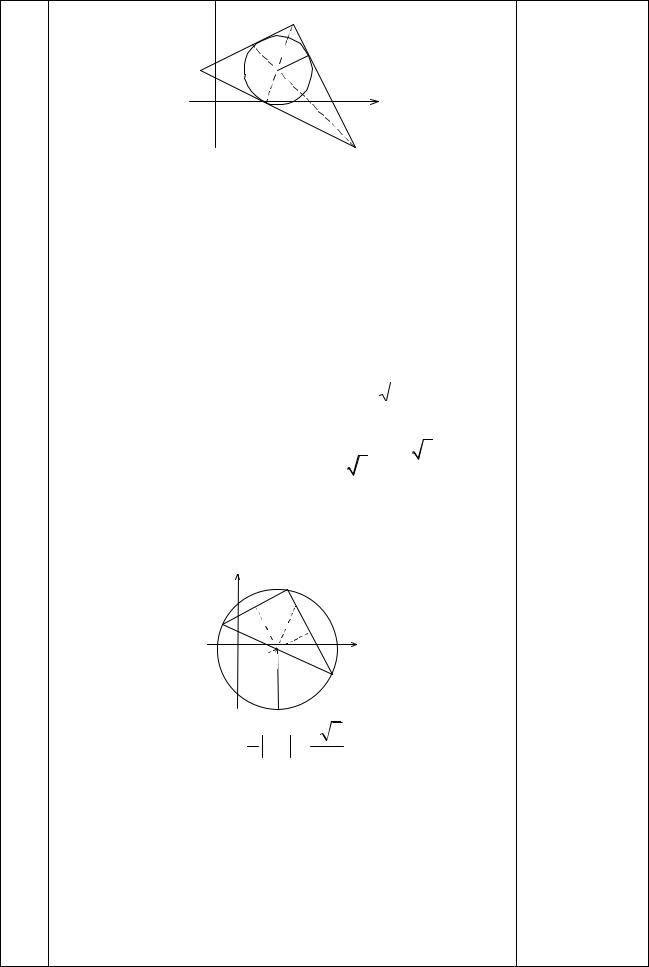
у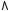

С

r

А

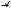
01

х

0

B

Система уравнений, составленная из уравнений биссектрис:

3х у 10 0,

у 2,

имеет решение х = 4, у = 2.

Следовательно, центр вписанной окружности находится в точке О1 (4, 2).

Радиус вписанной окружности найдем как расстояние

	от точки О1 до стороны АС: АС							x0 2			y	0	5			, где х0 =
											5
	4, у0 = 2.
							4 4			5
	Таким образом, r dAC
			AC
														5.
						5

з). Центр описанной окружности находится в точке пересечения серединных перпендикуляров. Для прямоугольного треугольника он лежит на середине гипотенузы.

уС

А	BB2 2
		A2	х
O0	O2
	R		B
	R

R 1 AB 5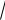5 . 2 2

и). Центр тяжести треугольника находится в точке пересечения медиан.

1). Из пункта в) имеем систему уравнений для определения координат центра тяжести как точки

11x 2 y 45 0,

пересечения медиан mС и mB :

13x 14y 75 0.

Система имеет решение х = 4,35, у = 1,45. Следовательно, центр тяжести треугольника находится

84

в точке О3 (4,35; 1,45).

2). Укажем, что медианы треугольника делятся точкой пересечения в отношении 2 : 1, считая от вершины.

Таким образом, координаты центра тяжести могут быть найдены как координаты точки О3, делящей медиану в

отношении СО3 2.

С3С2 1

Если воспользоваться формулами деления отрезка в данном отношении, то координаты точки:

x	xC	2xC			5 2 4
		2						4,33;
O		3			3
3
y		yC 2yC		2			5 2 ( 1 2)		1,33.
O		3			3
3

к). Внутренние углы.

Например, внутренний угол при вершине А треугольника может быть найден следующим образом:

cos A	AC AB								1 4						3
															5
	AC		AB							5 5
A arccos			3
						.
			5

л). По формуле площади треугольника имеем

			1			1	2	1			1
	1) S					9	3	1				60 30 (ęâ. ĺ ä.).
		2				5	5	1		2

2). Площадь треугольника может быть вычислена по формуле:

S = p r,

где p – полупериметр треугольника; r – радиус вписанной окружности.

Поскольку p 3 5 5 5 4 5 6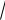5, a r 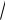5,

5
ňî S 30 (кв. ед.).
Найдите проекцию точки Р (4, 9) на прямую,
проходящую через точки А (3, 1) и В (5, 2).
2 РЕШЕНИЕ:	7,3
Искомую точку М x, y	найдем, решая совместно
уравнение прямой АВ с уравнением перпендикуляра,

85

		проведенного к этой прямой из точки Р.
		АВ :			х 3					у 1		у		1		х			1		.
						2			1			2					2
		Уравнение перпендикуляра из точки Р на прямую АВ
		ищем в виде у – 9 = k (x – 4);																				1
		из условия перпендикулярности k																					1 k 2.
			1				1										2
												x 7,
		y				x			,							М x, y = 7,3
			2
							2
												y 3.
		y 2x 17,
		Постройте прямую 3х – 5у + 15 = 0.
		РЕШЕНИЕ:
	3
		Уравнение							прямой			в отрезках имеет вид:													x			y	1,
																									5
																											3
		прямая отсекает на осях отрезки (-5) и 3.
		Даны две прямые 2х + 3у – 5 = 0, 7х +15у +1 = 0,
		пересекающиеся в точке М. Составьте уравнение
		прямой, которая проходит через точку М
		перпендикулярно к прямой 12х – 5у – 1 = 0.
		РЕШЕНИЕ 1:																2
		Прямые L : 2x 3y 5 0, k																		,
						1						1					7
													3
		L : 7x 15y 1 0, k2														пересекаются, так как они
	4	2										15																		5x 12y 6 0
		имеют разные угловые коэффициенты. Составим
		уравнение пучка прямых, проходящих через точку их
		пересечения М:
									2х + 3у – 5 + (7х + 15у +1) = 0,
						(2 + 7 ) х + (3 + 15 ) у + (-5 + ) = 0.
		Выделим в этом пучке искомую прямую L : y kx b.
		По условию искомая прямая перпендикулярна прямой
		L :	12х – 5у – 1 = 0, для которой k3																					12	. Угловой
		3															5

86

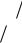
		коэффициент															искомой														кривой							k			1	,
			2 7								5																														k3
																							1 и										уравнение					искомой
			3 15
								12
		прямой принимает вид: 5х + 12у + 6 = 0.
		РЕШЕНИЕ 2:											2x 3y 5 0,
		Решая систему																													найдем точку пересе-
													7x 15y 1 0,
		чения прямых										26					,	37									. Каноническое уравнение
																		9
												3
																	x				26									y	37
		прямой имеет вид:																				3								9					или
																	12													5
		5x 12 y 6 0 .
		Напишите уравнение прямой L, проходящей через точку
		М (2, 1) под углом 45 к прямой
		L1: 2х + 3у +4 = 0.
			РЕШЕНИЕ:																					tg , L1: 2х + 3у +4 = 0,
				L : y k x b, k
															ó				2			x						4		k						2	..
												1						3							3					1		3
																																							1
															k k1													k		2 3										,			x 5y 3 0,
		45		0																															1 k1,2
	5				, tg																																		5 М
												1 k k1													1 (2 3) k
																																						5.					5x y 11 0
		(2,1) L,
																		3
								b ,
																		,
			y k x
		L :			1			1 b1,2										5
			y k2 x b2
																	11.
			y			1	x		3	,					x 5y 3 0,
		L :			5			5
															5x y 11 0.
			y 5x 11
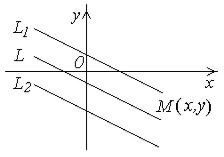
		Составьте уравнение прямой L, параллельной прямым
	6	L1: х + 2у – 1 = 0																																									х+2у+1/2=0
		и L2: х + 2у +2 = 0 и проходящей посередине между
		ними.

87

РЕШЕНИЕ:

Уравнение

прямой

L

будем

искать

в

виде

А(х – х0) + В(у + у0) = 0. В качестве нормального

вектора

n {A, B}

можно выбрать нормальный вектор

прямых L1

и L2, равный {1, 2}.

Найдем какую-нибудь точку М0 (х0, у0) L. Точка

М0 будет делить пополам отрезок, соединяющий две

любые точки, лежащие на L1 и L2. Например, М1 (1, 0)

L1 и М2 (-2, 0) L2, тогда точка М0 имеет координаты (-

1/2, 0), и уравнение прямой L принимает вид:

х + 2у + 1/2 = 0.

2. Кривые второго порядка

Найдите точки пересечения следующих линий:

1) (x – 1)2 + (y – 3)2 = 4 и (x – 3)2 + (y – 5)2 = 4;

2) (x – 5)2 + y2 = 1 и x + y = 0.

РЕШЕНИЕ:

x2 y2 2x 6 y 6 0,

вычитая

из

первого

1).

x2 y2 6x 10y 30 0,

1) (1, 5)

7

уравнения второе,

2

2

(3, 3).

получим систему x

y

2x

6y

6 0,

2)

y x 6,

решая

которую,

получаем

две точки

пересечения

(1, 5) и (3, 3);

2). Линии (x – 5)2 + y2 = 1

и

x

+ y

=

0

не

пересекаются,

так

как

система

уравнений

2

у

2

1, не имеет действительных решений.

(х 5)

х у 0

8

Составьте уравнение эллипса, фокусы которого лежат

х

2

у

2

1

на оси

абсцисс,

симметрично

относительно

начала

169

25

координат,

зная,

что

малая

ось равна

10,

а

88

эксцентриситет равен 12/13.

РЕШЕНИЕ:

Из условия имеем b = 5, е = 12/13. Поскольку

е = с/а и а2 = b2 + c2, то a2 = b2 + е2 a2 или

a2	b2	. Подставляя числовые значения, получим
1 e2		а2 = 169.

Следовательно, уравнение эллипса имеет вид:

									х2		у2
												1.
			169								25
Составьте уравнение эллипса, фокусы которого лежат
на оси абсцисс, симметрично относительно начала
координат, зная, что его большая ось равна 10, а
расстояние между фокусами равно 8.
РЕШЕНИЕ:													х2		у2
9			Из условия имеем а = 5, с = 4. Вычислим малую
																1
													25		9
полуось
b a2 c2									3.
							25 16
Следовательно, уравнение эллипса имеет вид:
	х2			у2
					1.
25			9
Фокусы гиперболы совпадают с фокусами эллипса

x2 y2 1. Составьте уравнение гиперболы, если ее

25 9

эксцентриситет равен 2.

РЕШЕНИЕ:

Из уравнения

эллипса

находим:

a2

25,

b2

9 . c2

a2

b2

16

, c

4.

ýëë

10

ýëë

ýëë

ýëë

ýëë

ýëë

c

x2

y2

1

По условию cýëë căčď c и eăčď

2 .

4

12

c

aăčď

Таким образом, a

2 и

b2

c2 a2

ăčď

2

16 4 12 .

ăčď

ăčď

Уравнение искомой гиперболы имеет вид: x2 y2 1. 4 12

89

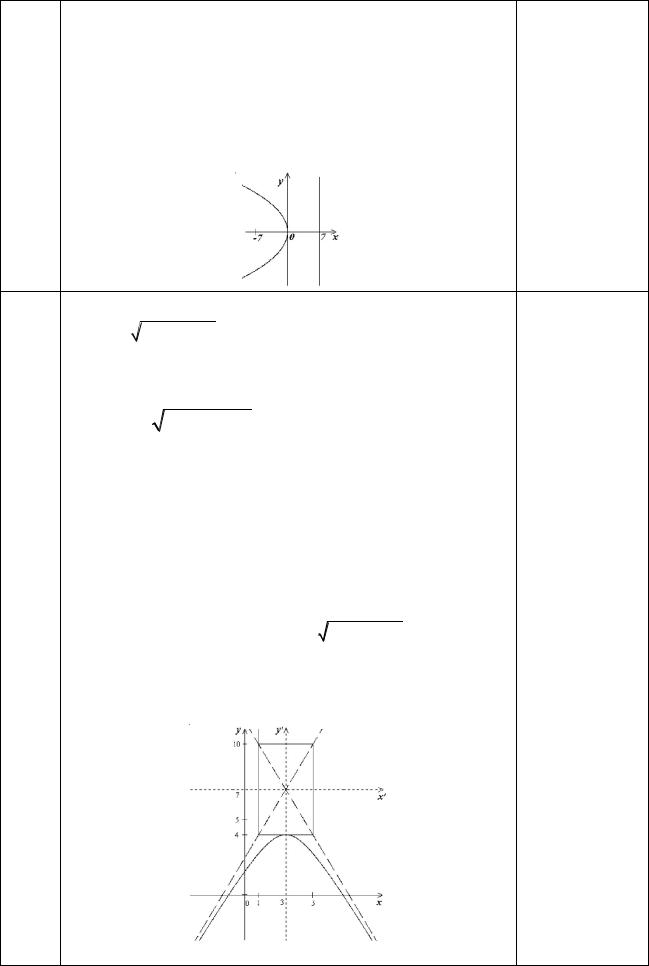
Составьте уравнение параболы, если известны ее фокус F(-7, 0) и уравнение директрисы

x – 7 = 0.

РЕШЕНИЕ:

Из уравнения директрисы имеем x = -p/2 = 7 или p = - 14.

11 Таким образом, уравнение искомой параболы имеет y2 = -28x

вид: y2 = -28x.

Установите,

какую линию

определяет

уравнение

3

y 7, x R. Нарисуйте ее график.

y 7

x2 6x 13,

2

РЕШЕНИЕ:

При

y 7

возведем

обе части

уравнения

3

y 7

x2 6x 13 в квадрат:

2

9

x2 6x 13

4

y 7 2 x2

6x 13 .

y 7 2

или

4

9

Выделяем в правой части полный квадрат:

4

y 7 2

x 3 2 4

или

(y 7)2

(x 3)2

1.

9

9

4

Это уравнение сопряженной гиперболы с центром в

Нижняя

точке О (3, 7) и полуосями а = 2, b = 3.

12

3

ветвь

2

y 7

x

6x 13,

определяет

сопряженной

2

Исходное уравнение

y 7

гиперболы

нижнюю

ветвь

сопряженной

гиперболы,

расположенную под прямой y=7.

90