Chast_10_TV

Министерство образования и науки Российской Федерации

Уральский федеральный университет имени первого Президента России Б. Н. Ельцина

МАТЕМАТИКА

Часть 10. Элементарная теория вероятностей

Екатеринбург

УрФУ

2014

УДК 519.21 (075.8) ББК 22.171.73

М 34

Авторы: Рыбалко А. Ф., Рыбалко Н. М., Лобашева Н. А., Магомедова Р. С.

Рецензенты:

кафедра физики Уральского государственного лесотехнического университета;

доктор физ-мат. наук, проф. А. П. Танкеев, зав. лабораторией ИФМ УрО РАН

МАТЕМАТИКА. Часть 10. Элементарная теория вероятностей:

М33 учебное пособие/ А. Ф. Рыбалко, Н. М. Рыбалко, Н. А. Лобашева,

Р.С. Магомедова. – Екатеринбург :УрФУ, 2014. – 227 с. ISBN

Пособие представляет собой десятую часть базового курса высшей математики и предназначено для бакалавров. Изложены элементы теории вероятности.

В работе представлены основные определения, формулировки теорем, примеры, демонстрирующие методы решения типичных задач. Если отсутствуют доказательства каких–либо утверждений, то формулировки результатов сопровождаются примерами, разъясняющими их смысл.

Пособие включает теоретические сведения, примеры решения задач, тексты домашних заданий, варианты индивидуальной расчетной работы и

справочный материал по данной теме.

УДК 519.21 (075.8) ББК 22.171.73

ISBN	Уральский федеральный университет, 2014

1. СЛУЧАЙНЫЕ СОБЫТИЯ. ОСНОВНЫЕ ПОНЯТИЯ.

ЭЛЕМЕНТЫ КОМБИНАТОРИКИ

Введение

Наблюдаемые события можно разделить на три группы: достоверные, невозможные, неопределенные. При создании определенных условий достоверные события обязательно происходят, невозможные — обязательно не происходят, неопределенные — могут

ипроизойти, и не произойти. Скажем, при подбрасывании монеты событие «монета упадет» — достоверное, событие «монета останется висеть в воздухе» — невозможное, событие «монета упадет гербом вверх» — неопределенное или случайное. Теорией вероятностей называется наука, изучающая закономерности в случайных явлениях.

Для того чтобы к неопределенному событию могли быть применены методы теории вероятностей, необходима возможность многократного наблюдения события при повторении комплекса условий. В рамках теории вероятностей термин случайное явление (событие) относится, как правило, именно к таким событиям, которые могут наблюдаться многократно. В этом случае события «матч выиграет команда А» или «Паша женится на Маше» — неопределенные, но не случайные в смысле, вкладываемом в это понятие в теории вероятностей: они не могут повториться при точно таких же условиях, при повторной встрече игроки будут в иной физической форме, молодые люди будут обладать иным опытом

ит.  п.

3

Элементы случайности присутствуют во всех явлениях природы. Во многих ситуациях случайными элементами пренебрегают, рассматривая вместо реального явления его детерминистическую (однозначно определенную) модель. Это схема точных наук: от условий опыта к его однозначному результату. Тем не менее во множестве задач необходимо учитывать случайные факторы, вносящие в результат опыта элементы неопределенности. Упрощенные схемы (математические модели) таких явлений носят название статистических, или вероятностных. Построение и исследование подобных моделей и составляет предмет теории вероятности и математической статистики.

1.1. Основные понятия

Пусть проводится некоторый опыт (как синонимы используются названия эксперимент, наблюдение, испытание), исход которого предсказать заранее нельзя.

Случайным событием (событием, исходом) называется любой исход опыта, который может произойти или не произойти. События обычно обозначаются заглавными латинскими буквами.

Пример: Опыт — бросание монеты; событие А — появление герба.

Элементарным исходом (элементарным событием) называют любой простейший (неделимый в условиях данного опыта) исход опыта. Элементарные исходы должны удовлетворять следующим условиям:

–в результате опыта один из исходов обязательно происходит;

–появление одного из элементарных исходов исключает появление остальных;

–в рамках данного опыта нельзя разделить элементарный исход на более мелкие составляющие.

Пример: При бросании игральной кости возможно появление 1, 2, 3, 4, 5, 6 очков, при этом появление 4 очков — событие элементарное, появление четного количества очков — событие не элементарное, оно составляется из 3 элементарных: появление 2, 4 или 6 очков.

Множество всех элементарных событий (исходов), связанных

сданным опытом, называют пространством элементарных событий

W, которое отождествляется с достоверным событием. Элементар-

ные исходы wi ОW — элементы этого множества.

4

Так как в дальнейшем события будут рассматриваться как некоторые множества, составленные из «более простых» событий, на-

	помним основные операции над множествами.
	Множеством называется любая совокупность
	объектов произвольной природы, каждый их кото-
	рых называется элементом множества. В дальней-
	шем множества (и события) будем обозначать боль-
	шими латинскими буквами, элементы — малыми
	латинскими, aО A — «элемент a принадлежит мно-
	жеству A ».
	В дальнейшем операции над событиями (и над
	множествами) будем иллюстрировать диаграммами
	Эйлера — Венна. В них пространство исходов изо-
	бражается на плоскости в виде прямоугольника,
	элементарные события — точками внутри прямо-
	угольника, более сложные события — подмноже-
	ствами точек прямоугольника.
	Пустым множеством называется множество, не
	содержащее ни одного элемента (обозначается Ø).	+
	Пустое множество соответствует невозможному со-
	бытию, т. е. такому, которое в данном опыте вообще
	не может произойти. Множество В называется под-
	множеством множества А, если все элементы В со-	–
	держатся в А. Обозначение B Н A .
	Пересечением (произведением) множеств А и В на-
	зывается множество D = A З B (D = A ґB , D = AB ),
	состоящее из элементов, входящих одновременно
	и в А, и в В.
	События А и В называются несовместными (непе-
	ресекающимися), если они не могут появиться вме-	Ω	Аn

	сте (их пересечение является невозможным событи- А1	А2
	ем, AB = Ж).
	Объединением (суммой) множеств А и В называ-
	ется множество C = A И B (C = A + B ), состоящее из

всех элементов, входящих хотя бы в одно из множеств А или В. (А и В см. на первом рисунке)

Разностью множеств А и В называется множество F = A B (

F= A - B ), состоящее из элементов, входящих в А, и не входящих

вВ. Противоположным событию A называется событие A , происхо-

5

дящее тогда и только тогда, когда не происходит событие A . Используется также термин дополнение события A : A = W - A . События A1, A2,...An образуют полную группу событий, если:

1) Ai Aj = Ж, i № j , 2) A1 + A2 +... + An = W .

Пример: Пространство элементарных событий W. Выпадение герба и выпадение решки при бросании монеты.

1.2. Вероятность. Варианты определения

Появление события A обладает какой-то степенью возможности, которую можно измерить численно. Это число называется вероятностью события.

Вероятность достоверного события, т. е. такого, которое в результате опыта неизбежно должно произойти, равна 1.

Вероятность невозможного события, т. е. такого, которое в данном опыте вообще не может произойти, равна 0.

Все события, возможные, но не достоверные, будут иметь вероятность между 0 и 1.

Пример: Выпадение герба и выпадение решки при бросании монеты.

1.2.1. Относительная частота события, статистическое определение вероятности

Пусть проведена серия из n испытаний при одних и тех же условиях; при этом фиксируется появление события A и событие A , которое произошло nA раз.

Число nA называют частотой наступления события A . Ясно, что

0 Ј nA Ј n.

Относительной частотой W ( A) события A называют отношение числа испытаний, в которых событие A появилось, к числу всех

проведенных испытаний: W (A) = nnA .

Если проводить серии опытов с большим числом испытаний при одинаковых условиях, то во многих случаях относительная частота наблюдаемого события будет мало меняться от серии к серии. Этот факт (статистическая устойчивость) проверен многократно в различных экспериментах.

Число, около которого группируются относительные частоты при увеличении числа испытаний, называется статистической веро-

ятностью рассматриваемого события:	P	(	A	)	= limW	(	A	)	= lim nA
					n®Ґ				n®Ґ n .
6

И относительная частота, и статистическая вероятность обладают следующими свойствами:

1. 0 Ј P (A) Ј 1, т. к. P (A) = lim nA , и nA і 0,n > 0 , nA Ј n.

n®Ґ n

2.P (W) = 1 , т. к. nA = n .

3.P (Ж) = 0 , т. к. n0 = 0 .

4. P (A + B) = P (A) + P (B) , если AB = Ж (события несовместны).

Основной недостаток статистического определения вероятности состоит в необходимости проведения большого числа опытов для вычисления вероятности в соответствии с этим определением.

1.2.2. Классическое определение вероятности

Событие называется благоприятствующим событию А, если появление этого события влечет за собой появление события А.

Пусть пространство элементарных событий Ω:

1)состоит из конечного числа элементарных исходов;

2)элементарные исходы w1,w2,...,wn равновозможны (нет оснований считать, что одни происходят чаще, чем другие).

Такая модель называется классической схемой. Эта схема применима к бросанию игральной кости: из симметрии кости вытекает равновозможность появления любого из чисел 1, 2, 3, 4, 5, 6.

Вероятностью события А называется отношение числа благоприятствующих этому событию исходов (исходов, составляющих событие А), к общему числу всех равновозможных исходов в конеч-

номерном пространстве элементарных событий, т. е. P(A) = nnA , где

nA — число благоприятствующих исходов, n — общее число несовместных равновозможных исходов, составляющих пространство исходов.

Свойства 1–4, рассмотренные для статистической вероятности, справедливы и для классической вероятности.

Пример: При бросании игральной кости из 6 случаев: 1,2,3,4,5,6 событию А — появление не менее 4 очков, благоприятны случаи 4,5,6, и неблагоприятны 1,2,3.

7

1.2.3. Геометрическое определение вероятности

Если число равновозможных исходов бесконечно и несчетно, то используется геометрическое определение вероятности.

Пусть каждый результат испытаний определяется случайным положением точки в некоторой области W (отрезок линии, фигура на плоскости, тело в пространстве), мера которой m(W) (под мерой области будем понимать длину, площадь, объем). Наступлению события А благоприятствует попадание точки в область A Н W. Веро-

ятность события А: P (A) = mm((WA)) , где m (A) — мера области А. Таким

образом, по геометрическому определению вероятность находится как отношение мер областей m (A) и m(W) .

Свойства 1–4, рассмотренные для статистической вероятности, справедливы и для геометрической вероятности.

Пример: (Задача о встрече) Двое договариваются встретиться в определенном месте. Встреча должна произойти в течение 1 часа (скажем, с 1200 до 1300). Пришедший первым ждет не более 15 минут, после чего уходит. Какова вероятность встречи?

Решение: Элементарный исход состо-

1

ит в том, что один участник появляется

0,75

в момент t1 , второй — в момент t2 , при-

чем

1

[

]

,

2

[

], т. е. исход ха-

t

О

12,13

t

О 12,13

действительных

0,5

рактеризуется

парой

чисел (t1,t2 ) и может быть изображен

0,25

точкой квадрата со стороной 1 на пло-

0

0,25 0,5 0,75

1

скости (выбор начала координат не вли-

яет на результат). Событие { 1

= t

2} благо-

0

t

приятствует

встрече

и

изображается

диагональю квадрата. Точки над диаго-

налью соответствуют событию { 1

> t

2} (первый пришел позже),

под диагональю — { 1

t

< t

2} (второй пришел позже). Благоприят-

t

1

2

}

и {

2

1

}.

ствующие встрече события: {

- t

< t

0

< t

Ј 0,25

0

- t

Ј 0,25

Этим событиям соответствуют изображенные на рисунке трапе-

ции над и под диагональю. Площадь квадрата S (W) = 1. Событию

A соответствуют заштрихованные области исходного квадра-

та, их площадь S (A) = 2

1

ж

9

ц

7

. P (A)

S (A)

7

.

Ч

Ч з1-

ч

=

=

=

2

16

16

S (W)

16

и

ш

8

Пример: (Задача Бюффона) Плоскость разграфлена параллельными прямыми на расстоянии L друг от друга. На плоскость наугад бросается игла (отрезок) длиной l < L. Найтивероятностьтого, что игла пересечет ка- кую–нибудь из прямых.

φ

π/2

0

L/2

Решение: Будем характеризовать исход опыта (положение иглы) двумя числами:

абсциссой x центра иглы относительно ближайшей прямой слева и углом j , который составляет игла с направлением прямых. Тот факт, что игла бросается на плоскость наугад, будем понимать так, что все значения x и j одинаково возможны. Не теряя общности, можно ограничить возможные значения x участком от 0 до L2 , j — от 0 до p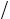2 , а возможность пересечения рассматривать только для одной из прямых (ближайшей левой). Пространство элементарных событий W —

прямоугольник со сторонами L2 и p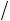2, SW = p4L . Игла пересечет

прямую, если абсцисса

ее центра будет меньше, чем (

)

sin j

;

x

{

(

)

}

l 2

интересующее нас событие

A =

. Область

за-

x <

l 2

sin j

A

штрихована

на рисунке,

ее

площадьS

= p 2

l

sin jdj =

l

,

A

SA

2l .

т0 2

2

P (A) = SW =

pL

Эта формула, полученная Бюффоном еще в XVIII веке, неоднократно подвергалась экспериментальной проверке, для чего подсчитывалась частота пересечений в длинной серии бросаний. С помощью этой формулы производилась даже приближенная оценка числа p и были получены вполне удовлетворительные результаты.

9

1.2.4. Аксиоматическое определение вероятности

Существует огромный класс событий, не обладающих симметрией возможных исходов, вероятности которых нельзя вычислить по классической формуле. В этом случае используется аксиоматический теоретико-множественный подход: рассматривается пространство исходов W; каждому исходу или множеству исходов A Н W, соответствующему некоторому событию А, ставится в соответствие вероятность события P ( A) — число, удовлетворяющее

следующим условиям:
1) Вероятность любого			события заключена		между 0 и	1:
0 Ј P(A) Ј1.
2) Вероятность достоверного события P (W) = 1 .
3) Если А и В	— несовместные события				( A ЧB = Ж ),	то
P(A + B) = P(A) + P(B)	или для любого числа событий A1, A2, , An ,
	ж	n	ц	n
если Ai Ч Aj = Ж при i № j , P з		е Ai ч		= еP (Ai ) , т. е. вероятность суммы
	и i=1		ш	i=1

несовместных событий равна сумме вероятностей этих событий.

A1, A2	, , An , или, для счетного множества несовместных событий
A1, A2	, , An, (Ai Ч Aj = Ж, i № j) ,	ж Ґ	ц	Ґ
		P з е Ai ч =		еP (Ai ).
		и i=1	ш	i =1
Следствия:
1.	Вероятность невозможного события P (Ж) = 0 .
2.	Если A Н B (событие А влечет		за	собой событие В), то

P(A) Ј P(B) .

3.Если события A и A противоположны, P(A) + P(A) = 1.

4.Если события A1, A2, , An образуют полную группу несовмест-

n	n
ных событий, т. е. если еAi = W, (Ai Ч Aj = Ж,	i № j), то еP(Ai ) =1.
i =1	i=1

1.3. Основные формулы комбинаторики

Рассмотрим наиболее часто встречающиеся при использовании классической схемы ситуации, требующие подсчета общего количества случаев и количества благоприятствующих случаев. При этом используются методы комбинаторики — раздела математики, изучающего задачи выбора элементов из заданного множества и расположения их в группы по заданным правилам.

10