Ch_7_Integraly_po_figure

МАТЕМАТИКА

Часть 7. ИНТЕГРАЛЫ ПО ФИГУРЕ

Министерство образования и науки Российской Федерации Уральский федеральный университет

имени первого Президента России Б.Н. Ельцина

Кафедра высшей математики

МАТЕМАТИКА

Часть 7. ИНТЕГРАЛЫ ПО ФИГУРЕ

Екатеринбург

УрФУ

2012

Министерство образования и науки Российской Федерации Уральский федеральный университет

имени первого Президента России Б.Н. Ельцина

МАТЕМАТИКА

Часть 7. ИНТЕГРАЛЫ ПО ФИГУРЕ

Курс высшей математики для бакалавров

Научный редактор – доц., канд. физ.-мат. наук Л.П. Мохрачева

Рекомендовано Уральским отделением Учебно-методического объединения вузов РФ в области строительного образования в качестве учебного пособия для студентов специальностей направления 270800 «Строительство» всех форм обучения

Екатеринбург

УрФУ

2012

УДК 517.37(075.8) ББК 22.161.1 я 73

К 78

Авторы: О.А. Кеда, Л.П. Мохрачева, А.Ф. Рыбалко, Н.М. Рыбалко

Рецензенты:

кафедра физики Уральского государственного лесотехнического университета; доктор физ-мат. наук, проф. А.П. Танкеев, зав. лабораторией ИФМ УрО РАН

Научный редактор – доц., канд. физ.-мат. наук Л.П. Мохрачева

К 78 МАТЕМАТИКА: учебное пособие Часть 7: ИНТЕГРАЛЫ ПО ФИГУРЕ / О.А. Кеда, Л.П. Мохрачева, А.Ф. Рыбалко, Н.М. Рыбалко. Екатеринбург:

УрФУ, 2012.-104 с.

ISBN

Данное издание представляет собой седьмую часть курса высшей математики и предназначено для бакалавров, программа обучения которых предусматривает равные количества аудиторных часов и часов для самостоятельной работы студентов.

Пособие включает теоретические сведения интегрирования по фигуре, примеры вычисления двойных и тройных интегралов, а также поверхностных и криволинейных интегралов первого рода, текст домашних заданий, пример оформления и задания индивидуальных расчетных работ, образец контрольной работы и справочный материал по теме.

Библиогр.: 5

Подготовлено кафедрой высшей математики

УДК 517.37(075.8) ББК 22.161.1 я 73

© Уральский федеральный университет имени первого Президента России Б.Н. Ельцина, 2012

	ОГЛАВЛЕНИЕ
I. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНТЕГРИРОВАНИЯ ПО ФИГУРЕ.................		4
1.	ИНТЕГРАЛЫ ПО ФИГУРЕ.................................................................................................	4
	1.1. Основные определения .................................................................................................	4
	1.2. Задача об отыскании массы тела ..................................................................................	6
	1.3. Определение интеграла по фигуре ...............................................................................	7
	1.4. Классификация интегралов по фигуре .........................................................................	7
	1.5. Свойства интегралов по фигуре ...................................................................................	8
	1.6. Геометрический смысл интегралов по фигуре ..........................................................	10
	1.7. Механический смысл интегралов по фигуре .............................................................	10
2.	ДВОЙНОЙ ИНТЕГРАЛ.....................................................................................................	10
	2.1. Геометрический смысл двойного интеграла..............................................................	10
	2.2. Вычисление двойного интеграла................................................................................	11
	2.3. Замена переменных в двойном интеграле..................................................................	15
	2.4. Двойной интеграл в полярных координатах..............................................................	18
3.	ТРОЙНОЙ ИНТЕГРАЛ......................................................................................................	20
	3.1. Задача о вычислении массы тела................................................................................	20
	3.2. Замена переменных в тройном интеграле..................................................................	23
	3.3. Тройной интеграл в цилиндрических координатах...................................................	24
	3.4. Тройной интеграл в сферических координатах .........................................................	25
4.	КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ПЕРВОГО РОДА ....................................................	27
	4.1. Криволинейный интеграл первого рода по плоской кривой.....................................	27
	4.2. Криволинейный интеграл первого рода по пространственной кривой ....................	28
	4.3. Геометрический смысл линейного интеграла по плоской кривой............................	28
5.	ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ПЕРВОГО РОДА ....................................................	29
	5.1. Вычисление поверхностных интегралов....................................................................	30
6.	ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛОВ
	ПО ФИГУРЕ .......................................................................................................................	31
	6.1. Длина, площадь, объем фигуры..................................................................................	31
	6.2. Масса фигуры..............................................................................................................	32
	6.3. Момент инерции фигуры............................................................................................	33
	6.4. Статические моменты фигуры. Центр тяжести фигуры............................................	35
II. ПРАКТИЧЕСКИЕ ЗАНЯТИЯ............................................................................		38
1.	Двойные интегралы и их приложения...............................................................................	38
2.	Тройные интегралы и их приложения ...............................................................................	44
3.	Криволинейные интегралы первого рода и их приложения.............................................	55
4.	Поверхностные интегралы первого рода и их приложения..............................................	59
III. ДОМАШНИЕ ЗАДАНИЯ.................................................................................		63
ДЗ № 1. Двойные интегралы..................................................................................................		63
ДЗ № 2. Тройной интеграл.....................................................................................................		67
ДЗ № 3. Криволинейные и поверхностные интегралы 1 рода.............................................		68
IV. РАСЧЕТНАЯ РАБОТА.....................................................................................		71
1.	Титульный лист ..................................................................................................................	71
2.	Варианты заданий...............................................................................................................	72
V. ФОРМУЛЫ.........................................................................................................		97
VI. БИБЛИОГРАФИЧЕСКИЙ СПИСОК ............................................................		104

3

I. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНТЕГРИРОВАНИЯ ПО ФИГУРЕ

1.ИНТЕГРАЛЫ ПО ФИГУРЕ

1.1.Основные определения

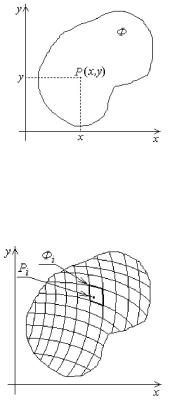
Впланиметрии (стереометрии) принято называть фигурой произвольное подмножество плоскости (пространства). Таким образом, по сложившейся традиции в классической геометрии слово "фигура" употребляется вместо слова "множество". В этом разделе необходимо дать аналитическое определение фигуры, которое будет использовано при определении кратных интегралов и поверхностных и криволинейных интегралов первого рода.

Дадим некоторые вспомогательные определения.

ОПРЕДЕЛЕНИЕ

Пусть функции t и t непрерывны на сегменте , . Тогда множество

точек M x, y , где x t , y t , задает простую плоскую кривую L, если различным значениям параметра t соответствуют различные точки плоскости.

Замечание

Если функции t , t	и t непрерывны на сегменте , , то множе-
ство точек M x, y, z , где	x t , y t , z t , задает простую про-

странственную кривую L, если различным значениям параметра t соответствуют различные точки пространства.

ОПРЕДЕЛЕНИЕ

Пусть L1 и L2 − две простые плоские кривые на , с совпадающими гра-

ничными точками и несовпадающими любыми неграничными точками. Тогда объединение этих кривых образует замкнутую простую плоскую кривую.

ОПРЕДЕЛЕНИЕ

Пусть функция z z x, y непрерывна в плоской области G, ограниченной замкнутой простой кривой L . Множество точек M x, y, z x, y задает простую

поверхность , если различным точкам P x, y G соответствуют различные точки М.

ОПРЕДЕЛЕНИЕ

Пусть 1 и 2 − две простые поверхности, заданные в области G с совпадающими граничными точками и несовпадающими любыми не граничными точками. Тогда объединение этих поверхностей образует замкнутую простую поверхность.

ОПРЕДЕЛЕНИЕ

Вдальнейшем под фигурой Ф будем понимать:

1)отрезок a,b оси Ox;

2)часть плоскости XOY, ограниченной простой замкнутой плоской кривой L;

3)часть трехмерного пространства G, ограниченного простой замкнутой поверхностью (тело);

4

4)простую плоскую или пространственную кривую L , заданную на сегменте , ;

5)простую поверхность в пространстве, заданную в плоской области G, ог-

раниченной замкнутой простой кривой L.

Замечание

Из данного определения следует, что фигура есть ограниченная, замкнутая, связная область.

ОПРЕДЕЛЕНИЕ

Диаметром d фигуры Ф называется максимальное расстояние между двумя точками фигуры. Например, на рисунке d AB .

ОПРЕДЕЛЕНИЕ

Длина отрезка кривой определяется как точная верхняя грань длин, вписанных в кривую ломаных. Если длина кривой существует и конечна, то говорят, что кривая спрямляемая, в противном случае — неспрямляемая.

ОПРЕДЕЛЕНИЕ

Плоская фигура F называется квадрируемой, если для любого e 0 существует пара многоугольников P и Q, такие, что P F Q и

S Q S P e , где S(P) обозначает площадь многоугольника P.

Многоугольники, содержащие фигуру F и содержащиеся в фигуре F, можно составить из одинаковых квадратов, откуда и возник термин «квадрируемость». При уменьшении размеров квадратов разность площадей многоугольника, содержащего фигуру, и многоугольника, содержащегося в фигуре, должна стремиться к нулю.

Следующее утверждение связывает эти два понятия.

Теорема

Если граница L плоской фигуры Q представляет собой спрямляемую кривую, то фигура Q квадрируема.

Площадь многогранных поверхностей определяется как сумма площадей их плоских граней. В качестве более широкого класса чаще всего рассматривают кусочно-гладкие поверхности с кусочно-гладким краем (или без края). Для них площадь поверхности обычно определяют с помощью следующей процедуры:

1)поверхность разбивают на мелкие части с кусочно-гладкими границами;

2)в каждой части выбирают точку, в которой существует касательная плоскость;

5

3)ортогонально проектируют рассматриваемую часть на касательную плоскость поверхности в выбранной точке;

4)площадь полученных плоских проекций суммируют;

5)переходят к пределу при всё более мелких разбиениях (таких, что

наибольший из диаметров частей разбиения стремится к нулю).

При определении понятия кубируемого тела повторяется предыдущее определение квадрируемости, но квадраты заменяются на кубы. Разность объемов тел, составленных из одинаковых кубиков, из которых бòльшее тело содержит, а меньшее – содержится в рассматриваемом теле G, должна стремиться

кнулю при уменьшении размеров кубиков.

Вдальнейшем в качестве областей интегрирования будем рассматривать только измеримые фигуры, т.е. такие фигуры, которым можно сопоставить

меру. ОПРЕДЕЛЕНИЕ

Под мерой μ будем понимать для фигур:

1)длину отрезка a,b , μ b a ;

2)площадь плоской области D, μ S ;

3)объем трехмерного тела G, μ V ;

4)длину кривой L, μ l ;

5)площадь поверхности , μ Sï î âåðõ. .

Изложенные выше требования означают, что кривые должны быть спрямляемыми, плоские области и поверхности – квадрируемыми, трехмерные тела –

кубируемыми.

1.2. Задача об отыскании массы тела

Пусть фигура Ф обладает массой, распределенной по всей фигуре. В каждой точке фигуры P распределение массы описыва-

ется плотностью ρ P . Зададим плотность ρ P в виде:

ρ x ,

ρ P ρ x, y ,

ρ x, y, z ,

если соответственно Ф – отрезок, плоская область или объект, протяженный в трех измерениях (линия, поверхность или тело).

Найдем массу фигуры в случае, если Ф − часть плоскости XOY: ρ P ρ x, y .

1.Рассмотрим случай однородного распределения плотности по фигуре, т.е. ρ P const. Следовательно, m ρ P μ .

2.В случае, если ρ P const, разобьем фигуру Ф про-

извольным образом на n элементарных областей Фi ,			с
кусочно-гладкими	границами,	таких,	что

6

Ф1 Ф2 ... Фn Ф ,		Фi Фj 0, i j ,		и выберем точку Pi i . Пусть n
достаточно	велико,	чтобы	полагать	в	каждой элементарной	фигуре
ρ Pi const.	Обозначим μi		– меру каждой		элементарной фигуры Фi.	Масса

элементарной

n

фигуры: mi ρ Pi μi . Масса всей фигуры m ρ Pi μi .

i 1

1.3. Определение интеграла по фигуре

Пусть дана фигура Ф и функция f P , P , определенная на множестве Ф. Разобьем фигуру Ф произвольным образом на n элементарных

областей Фi и выберем точку Pi i . Вычислим f Pi	и составим интеграль-
n
ную сумму вида: Sn f Pi μi , соответствующую данному разбиению.
i 1
Для каждой элементарной фигуры Фi найдем диаметр di ; наибольший из
диаметров обозначим rn и назовем рангом разбиения,	rn max di . В дальней-
	i 1,2,...,n

шем будем рассматривать только такие последовательности разбиений, для ко-

торых rn 0

при n .

ОПРЕДЕЛЕНИЕ

Интегралом по фигуре Ф (обозначение f P dμ ) будем называть предел

Ф

интегральной суммы Sn

при rn 0, если этот предел существует и не зависит

от

способа

разбиения

и

выбора

точек

Pi .

Таким

образом,

f P dμ lim

n

f P μ

, Ф – область интегрирования.

i

r 0

i

Ф

n

i 1

1.4. Классификация интегралов по фигуре

1.

Пусть фигура

–

часть

прямой,

a,b ,

f P f x ,

dμ dx ,

b

f P dμ f x dx – определенный интеграл по отрезку a,b .

a

f P f x, y ,

2.

Фигура

–

часть

плоскости

XOY,

D ,

dμ dS ,

f P dμ f x, y dS

– двойной интеграл от функции

f P f x, y по

D

области D.

f P f x, y, z ,

3.

Фигура – пространственная область, G ,

dμ dV ,

f P dμ f x, y, z dv

–

тройной

интеграл

от

функции

G

f P f x, y, z по области G.

4.

Фигура

–

линия

на

плоскости

или в

пространстве,

L ,

f P f x, y

или

f P f x, y, z , dμ dl ,

f P dμ f x, y dl или

L

7

	f P dμ f x, y, z dl			– криволинейный интеграл от функции			f P по
		L
	кривой L.		поверхность,		,	f P f x, y, z ,	dμ dσ ,
5.	Фигура	–
	f P dμ	f x, y, z dσ		–	поверхностный интеграл от		функции
	f P f x, y, z по области .
Теоремы существования интеграла по фигуре
1.	Если функция		f P непрерывна в двумерной (трёхмерной) ограниченной,

замкнутой области Ф с границей меры нуль, то она интегрируема в этой облас-

ти, т.е. интеграл	f P dμ f x, y dS		( f P dμ f x, y, z dv ) сущест-
вует.		D		G
2. Пусть L – плоская или пространственная гладкая кривая (т.е. задающие её
функции x t ,	y t	( x t , y t , z t ) непрерывны на сегмен-

те , и имеют на нём непрерывные производные, не обращающиеся одно-

временно в нуль). Тогда если функция f P		непрерывна на L, то она интегри-
руема, т.е. существует интеграл f P dμ f x, y dl
		L
( f P dμ f x, y, z dl ).
	L
3.	Пусть – гладкая поверхность z z x, y , заданная в ограниченной
замкнутой области G. Тогда если функция		f P непрерывна на , то она ин-
тегрируема, т.е. существует интеграл f P dμ f x, y, z dσ .

Замечание. Непрерывность на кривой и поверхности определяется как непрерывность в сколь угодно малой, но конечной двумерной (для плоской кривой) или трёхмерной области (для пространственной кривой и кривой поверхности), целиком содержащей данную фигуру.

1.5. Свойства интегралов по фигуре

Доказательства свойств интегралов следуют из определения интеграла по фигуре Ф.

Свойства, определяемые равенствами

1. Линейное свойство. Если функции f P и g P интегрируемы

по фигуре Ф, то функция f P g P , где , R , также интегрируема по

Ф и имеет место равенство f P g P dμ f P dμ g P dμ .

8