§. Основные свойства определённого интеграла.

А.Условие нормировки.. ∆. ▲

В. Линейность. Множество функций интегрируемых по Риману на [a,b] –R_{[a, b]}является линейным пространством относительно операции + и · (сложения и умножения на число).

На этом пространстве определённый интеграл есть линейный функционал f,gR_{[a, b]}

, ℝ  (f +g) R[a,b] и.

∆ =

= , и, переходя к пределу при, получим

.

С.Монотонность.Интеграл от неотрицательной интегрируемой функции неотрицателен

fR_{[a, b]} и x[a, b] f(x)  0  . ∆. ▲

D.Интегрирование неравенств. Нестрогое неравенство между интегрируемыми функциями сохраняется при почленном интегрировании

f, gR_{[a, b]} x[a, b] f(x)  g(x)  .

∆ . ▲

*.Строгое неравенство между интегрируемыми функциями не сохраняется

f, gR_{[a, b]} x[a, b] f(x) < g(x)  .

Е.Интегрируемость по подпромежутку. Если функция интегрируема по промежутку, то она интегрируема по любому его подпромежутку.

∆ fR_{[a, b]} [c, d]  [a, b]  f(x)R_{[c, d]}. ▲

F

. Аддитивность определенного интеграла, как функции ориентированного промежутка.

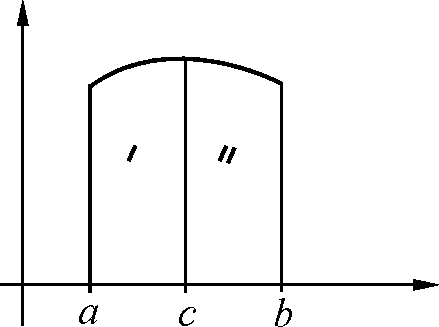
a,b,c If R_I, причем равенство справедливо независимо от взаимного расположения точекa,b,c.

1. a < c < b: .

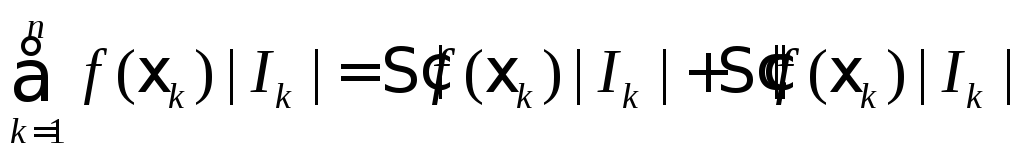Устремляя _P  0, получаем.

b)c=a.

c)Легко видеть, если записать, соответствующие интегральные суммы .

G

.Условие положительности определённого интеграла от неотрицательной функции.

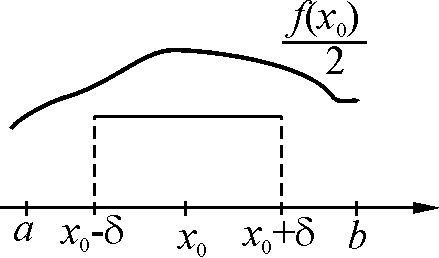
Интеграл от неотрицательной интегрируемой функции положителен, если на промежутке есть точка, в которой функция положительна и непрерывна. f(x)R_{[a, b]}a<bx[a,b] f(x)0

и x₀[a,b]f(x₀) > 0 иf непрерывна вx₀.

Тогда .

∆ x₀[a,b] 1)f(x₀) непрерывна вx₀> 0> 0x|x–x₀| <|f(x) –f(x₀)| <,

значит f(x) –<f(x₀) <f(x₀) +.

2) Выберем .ТогдаxO(x₀,).

И построим функцию

.

x[a,b] f(x)g(x). ▲

H.Равенство нулю интеграла от интегрируемой функции, почти всюду равной нулю.

fR_{[a, b]}и f(x) = 0 почти всюду (п.в.) на [a,b].

∆ . ▲

I.Условия обращения в нуль интеграла от неотрицательной функции. В случае существования интеграл равен нулю, если функция равна нулю почти всюду.

fR_{[a, b]} x[a, b] f(x)  0 (п.в.) на [a, b]. ∆▲

J.Равенство интегралов от функций, которые равны п.в.Интегралы от функций, которые равны почти всюду, равны между собой

f,gR_[a,b] f(x) = g(x) п.в. на [a, b]  .

∆ F(x) = f(x) – g(x) R_{[a, b]} и F(x) = 0 п.в. на [a, b] . ▲

K.Возможность неопределённости подынтегральной функции на множестве лебеговой меры ноль. Под знаком интеграла может стоять функция, которая не определена на подмножестве промежутка интегрированная лебеговой меры ноль. Если доопределить или переопределить подынтегральную функцию на множестве лебеговой меры ноль, то интеграл не изменится. Любое такое доопределение, если оно, возможно, даёт одно и то же значения интеграла.

В частности, на конечном множестве точек ограничений на выбор частичных значений подынтегральной функции нет.

, где. ∆▲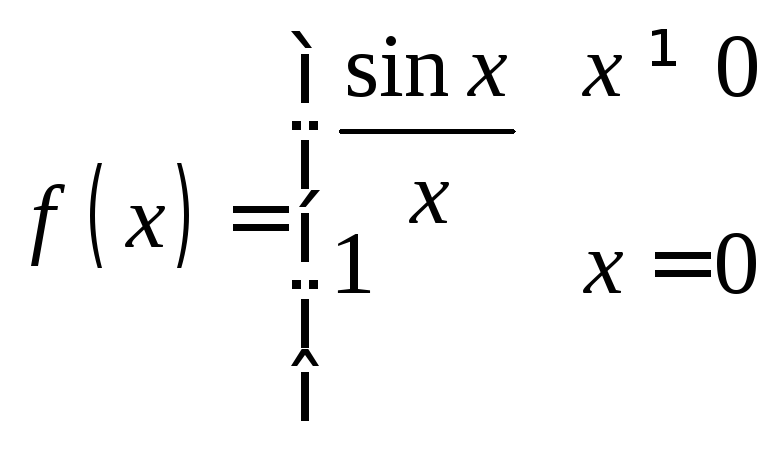

L.Интегрируемость модуля интегрируемой функции и неравенство между соответствующими интегралами. Если функция интегрируема по промежутку, то её модуль по этому же промежутку также интегрируем. При этом: модуль интеграла от функции не превышает интеграла от модуля той же функции. f R_{[a, b]}| f|R_{[a, b]} .

∆ Т.к. – | f (x) |f (x)|f (x) |. ▲

M.Первая теорема о среднем. Если функцииfиg интегрируемы на [a,b], причём одна

из них не меняет знак на [a,b], а значение другой находится между значениямиmиM, то найдётся числотакое, чтоmM и интеграл от произведения этих функций равен произведениюна интеграл от той функции, которая не меняет знак на [a,b].

f, g R_[a,b] g(x)  0 x[a, b] (или g(x)  0 x[a, b]) и x[a, b] – < m  f(x)  M < +

 [m, M] .

Если функция, среднее значение которой выносится из под знака интеграла, непрерывна на промежутке интегрирования, то указанное среднее значение является одним из значений этой функции внутри промежутка интегрирования.

fC_{[a, b]}c (a,b)=f(c).



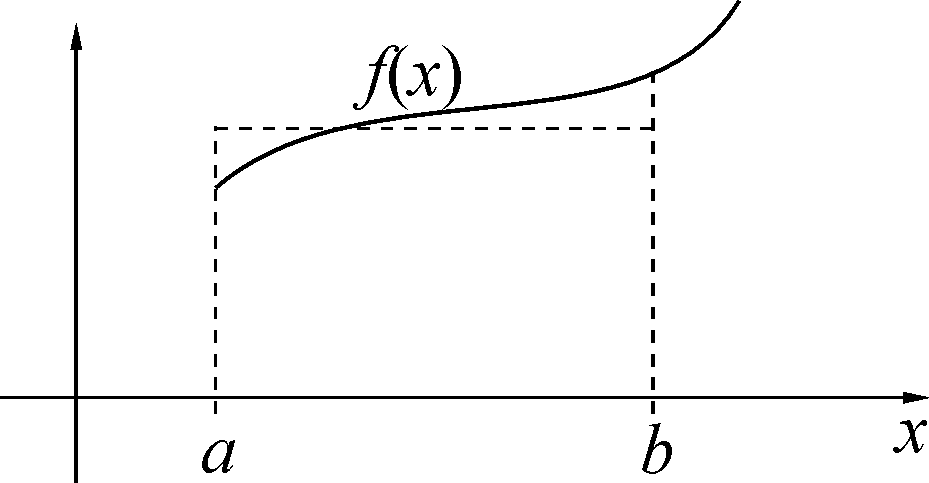
В частности. При этомназывается средним значением функции на промежутке [a,b]. Смысл названия среднее значение иллюстрируется на рисунке справа.

 m  f(x)  M; g(x)  0  m g(x)  f(x) g(x)  M g(x)

. И далее два варианта

а) m00 =0.

б) .

N.Вторая теорема о среднем.Формулы Бонне.

Если и функцияf (x) монотонна на, то, такое что

.

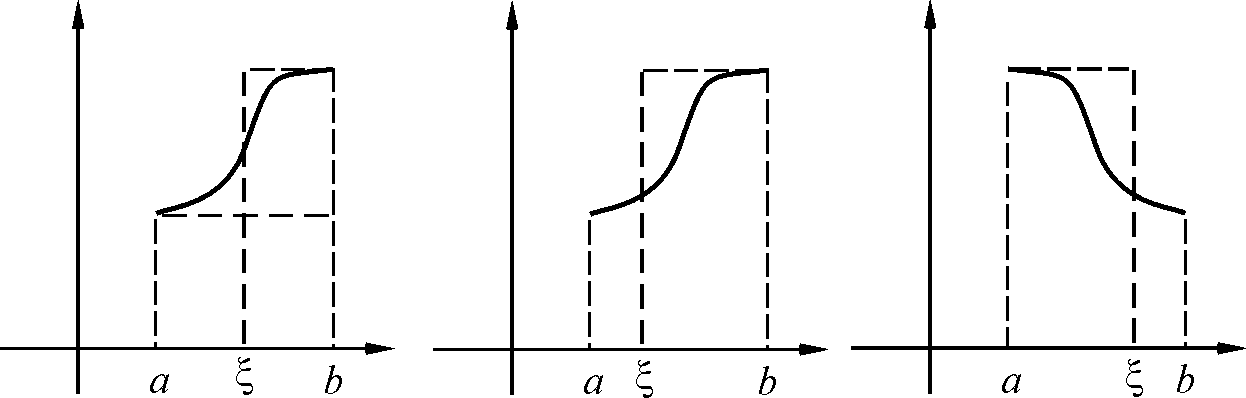
Кроме того, известны две разновидности второй теоремы о среднем, называемые формулами Бонне

а). Еслиf(x) – неотрицательная и не убывающая.

б). Еслиf (x) – неотрицательная и не возрастающая

Рисунки иллюстрируют геометрический смысл второй теоремы о среднем и формул Бонне.