7. Простые алгоритмы. Длина отрезка апериодичности

Большинство ал­горитмов, используемых на практике для получения псевдослучайных чисел, представляют собой рекуррент­ные формулы первого порядка

(4)

где начальное число задано. Легко показать, что функция y= Ф (x), изображенная на

Y Y

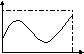
0 1 Х 0 1 Х

Рис. 3. Рис. 4.

породить хорошую последовательность псевдослучайных чисел ... В самом деле, если по настоящим случайным числам построить точки с координатами (), () то они равномерно распределены в единич­ном квадрате 0<x<1, 0<у<1, в то время как соот­ветствующие точки, построенные по числам (4),

располагаются на кривой у ==Ф (х).

Следовательно, «хорошую» последовательность мо­жет породить только такая функция

у =Ф (х), график которой весьма плотно заполняет единичный квадрат. Примером такой функции может служить функция у =Д (gx) при очень больших g (рис. 4). И действитель­но, эта функция послужила основой для ряда методов получения псевдослучайных чисел.

Конечно, приведенное условие только необходимо, но далеко не достаточно для того, чтобы формула (4) порождала «хорошие» псевдослучайные числа.

Другая важная черта алгоритмов вида (4) — то, что при реализации их на ЭВМ они всегда порождают периодические последовательности. В самом деле, так как в коде любой ЭВМ можно записать лишь конечное чис­ло N чисел, заключенных между нулем и единицей, то рано или поздно какое-нибудь значение совпадает с одним из предыдущих значений . Тогда в силу (4)

, при i=1, 2,… (5)

Пусть L— наименьшее число, удовлетворяющее (5) при некотором l (l<L); множество чисел

Рис, 5.

называется отрезком апериодичности последовательно­сти (4), число I —длиной отрезка апериодичности, а Р =L - l —длиной периода (рис. 5).

Очевидно, в рассматриваемом случае отрезок апери­одичности состоит из различных чисел. И обычно для расчета не рекомендуют использовать больше чем I* чисел последовательности (4). Ясно также, что LN.

Для экспериментального определения I и Р можно рекомендо­вать следующий алгоритм, Выбирается целое число Т (и несколько раз меньшее, чем предполагаемое значение L. Вычисляются подряд числа .....причем запоминаются, и все

из отрезка рТ<i(р+1)Т сравниваются со всеми Как только окажется выполненным равенство, вычисляется длина периода Р =-mТ и число t= - рТ.

Чтобы вычислить L, по числу вычисляется после чего считаются и сравниваются между собой две последова­тельности значений: и при Не позднее чем при j = t +T произойдет совпадение этих значений. Если совпадение произойдет при , то .

9. Алгоритм д. Неймана

Первый алгоритм для получения псевдослучай­ных чисел был предложен Дж. Нейманом. Его называют методом середины квадрата.

В этом методе число предполагается 2k-значным: =0,

Чтобы получить число надо возвести в квадрат

и затем отобрать средние 2k цифр этого квадрата:

Нетрудно проверить, что этому методу соответствует функция или, что то же,

Однако от метода середины квадрата вычислители отказались, так как в последовательностях, построенных таким образом, получается больше, чем нужно, малых чисел.