
1 Рис. 12 7. Касательная плоскость и нормаль к поверхности
Рассмотрим
некоторую поверхность S
и на ней точку
![]() (рис. 12).
(рис. 12).
Плоскость
![]() называется касательной плоскостью
к поверхности S
в точке
называется касательной плоскостью
к поверхности S
в точке
![]() на ней, если расстояние
на ней, если расстояние
![]() от переменной точки
от переменной точки
![]() поверхности S
до этой плоскости, при стремлении
расстояния
поверхности S
до этой плоскости, при стремлении
расстояния
![]() к нулю, является бесконечно малой
высшего порядка, чем
к нулю, является бесконечно малой
высшего порядка, чем
![]() .
.
Можно дать и другое определение этому понятию.
Если
через точку
![]() на поверхности S
провести множество гладких кривых,
то все касательные к этим кривым в точке
на поверхности S
провести множество гладких кривых,
то все касательные к этим кривым в точке
![]() лежат в плоскости, которая является
касательной плоскостью к поверхности
S
.
лежат в плоскости, которая является
касательной плоскостью к поверхности
S
.
Для того чтобы
поверхность
![]() в точке
в точке
![]() ,
где
,
где
![]() ,
имела касательную плоскость, необходимо
и достаточно, чтобы при
,
имела касательную плоскость, необходимо
и достаточно, чтобы при
![]() и
и
![]() функция
функция
![]() была дифференцируема.
была дифференцируема.
Уравнение касательной
плоскости к поверхности, заданной
уравнением
![]() ,
в точке
,
в точке
![]() ,
лежащей на этой поверхности:
,
лежащей на этой поверхности:
![]()
или
![]() .
.
Вектор
![]() нормали к касательной плоскости,
то есть
нормали к касательной плоскости,
то есть
![]() ,
называется вектором нормали (или
нормалью) к поверхности
,
называется вектором нормали (или
нормалью) к поверхности
![]() в точке
в точке
![]() .
.
Уравнение нормали имеет вид:
![]()
Касательная плоскость
к поверхности, заданной неявно
уравнением
![]() в точке
в точке
![]() ,
лежащей на этой поверхности, определяется
уравнением
,
лежащей на этой поверхности, определяется
уравнением
![]()
а
нормаль к поверхности в точке
![]() – уравнениями
– уравнениями
![]()
Пример
16. К поверхности
![]() провести касательные плоскости,
параллельные плоскости
провести касательные плоскости,
параллельные плоскости
![]() .
.
Решение. Уравнение
поверхности имеет вид
![]() .
Найдём частные производные:
.
Найдём частные производные:
![]()
Нормальный
вектор заданной плоскости
![]() .
Нормальный вектор искомой касательной
плоскости
.
Нормальный вектор искомой касательной
плоскости
![]()
Из условия параллельности
касательной и заданной плоскостей
следует, что
![]() ,
т.е. их координаты пропорциональны:
,
т.е. их координаты пропорциональны:
![]()
Присоединим к данным уравнениям уравнение поверхности и найдём координаты точек касания:
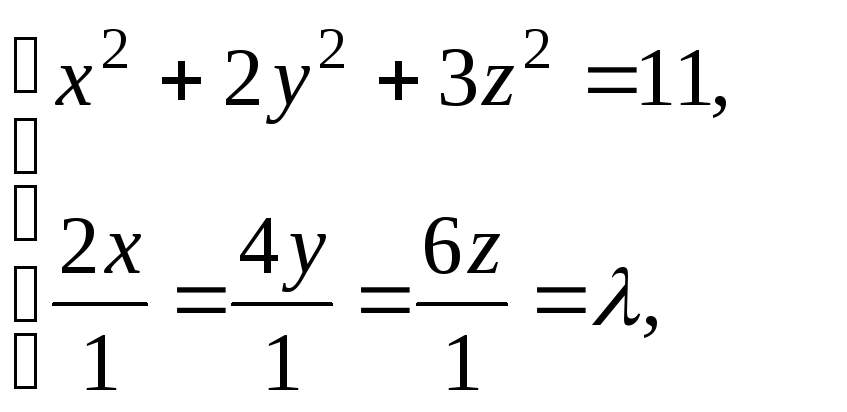
![]()
Подставляя найденные
значения
![]() в уравнение поверхности, получаем:
в уравнение поверхности, получаем:
![]()
откуда
![]()
Следовательно, получаем
две точки касания с координатами
![]() и
и
![]() ,
через которые проходят две плоскости,
являющиеся касательными к данной
поверхности. Их уравнения имеют вид:
,
через которые проходят две плоскости,
являющиеся касательными к данной
поверхности. Их уравнения имеют вид:

т.е.
![]() и
и
![]()
Пример 17. Составить
уравнения касательной плоскости и
нормали к параболоиду
![]() в точке
в точке
![]() .
.
Решение.
![]() =
=![]() .
Находим
.
Находим
![]()
![]()
Тогда, подставляя эти значения в уравнение
![]() ,
,
получим уравнение касательной плоскости к параболоиду в заданной точке:
![]() или
или
![]() .
.
Вектор
![]() является вектором нормали к параболоиду
в заданной точке. Поэтому уравнение
нормали будет следующим:
является вектором нормали к параболоиду
в заданной точке. Поэтому уравнение
нормали будет следующим:
![]()
18. Формула Тейлора
Из теории функций
одной переменной мы знаем, что если
функция
![]() в точке
в точке
![]() имеет производные до
имеет производные до
![]() порядка включительно, то она может быть
разложена в окрестности этой точки по
формуле Тейлора следующим образом:
порядка включительно, то она может быть
разложена в окрестности этой точки по
формуле Тейлора следующим образом:
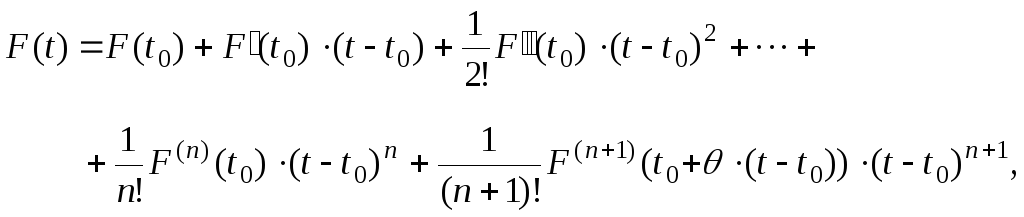
где
![]() – остаточный член (в форме Лагранжа),
– остаточный член (в форме Лагранжа),
![]() .
.
Положив
![]() ,
,
![]() ,
,
и вспомнив, что
![]() ,
,
эту формулу можно переписать в виде
![]() ,
,
Именно эту формулу мы и применим для случая функции многих переменных.
Для простоты записи ограничимся случаем функции двух переменных.
Пусть
в окрестности некоторой точки
![]() функция
функция
![]() имеет непрерывные производные всех
порядков до
имеет непрерывные производные всех
порядков до
![]() -го
включительно. Придадим значениям
переменных
-го
включительно. Придадим значениям
переменных
![]() и
и
![]() некоторые приращения
некоторые приращения
![]() и
и
![]() ,
такие, чтобы отрезок прямой, соединяющий
точки
,
такие, чтобы отрезок прямой, соединяющий
точки
![]() и
и
![]() не вышел за пределы рассматриваемой
окрестности точки
не вышел за пределы рассматриваемой
окрестности точки
![]() .
.
Введем
новую независимую переменную
![]() ,
,
![]() ,
положив
,
положив
![]() ,
,
![]() .
.
Эти
формулы задают некоторый прямолинейный
отрезок, соединяющий точки
![]() и
и
![]() .
.
Подставив
эти выражения для
![]() и
и
![]() в функцию
в функцию
![]() ,
получим сложную функцию одной переменной
,
получим сложную функцию одной переменной
![]() :
:
![]() .
.
Но тогда
![]()
![]()
![]() .
.
А
![]() – функция одной переменной и в точке
– функция одной переменной и в точке
![]() имеет непрерывные производные до
имеет непрерывные производные до
![]() порядка включительно, следовательно,
она может быть разложена в окрестности
этой точки по полученной выше формуле
Тейлора следующим образом:
порядка включительно, следовательно,
она может быть разложена в окрестности
этой точки по полученной выше формуле
Тейлора следующим образом:
![]()
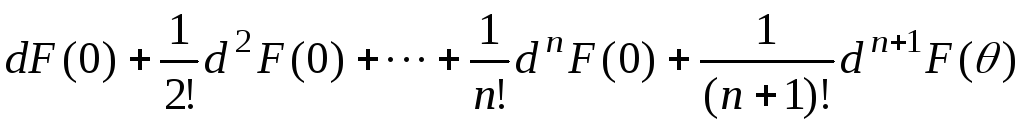 ,
,
![]() .
.
При
этом дифференциал
![]() ,
входящий в правую часть формулы в
различных степенях, равен
,
входящий в правую часть формулы в
различных степенях, равен
![]() .
.
Известно, что при линейной замене переменных свойство инвариантности формы дифференциала имеет место и для высших дифференциалов. Поэтому, можно записать, что
![]() ,
,
![]() ,
,
и
т.д. И для
![]() -го дифференциала будем иметь формулу
-го дифференциала будем иметь формулу
![]()
Заметим,
что здесь дифференциалы
![]() и
и
![]() ничем не отличаются от ранее взятых
приращений
ничем не отличаются от ранее взятых
приращений
![]() и
и
![]() ,
т.к.
,
т.к.
![]() ,
,
![]() .
.
Тогда
для функции
![]() справедлива формула
справедлива формула
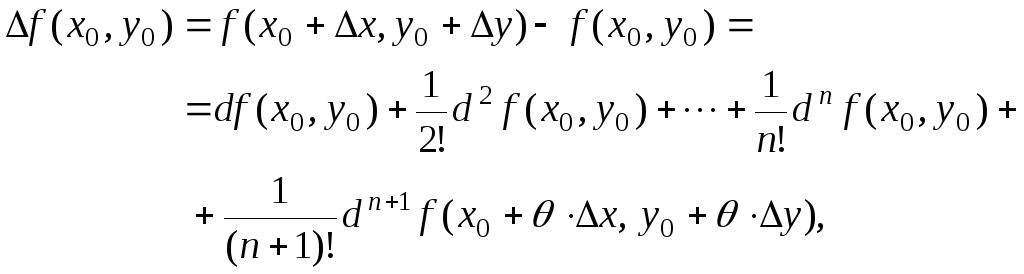 (17)
(17)
![]() ,
,
называемая формулой Тейлора в дифференциальной форме.
Заметим,
что фигурирующие в этой формуле справа
дифференциалы переменных
![]() и
и
![]() (скрытые в дифференциалах функции)
равны именно тем приращениям
(скрытые в дифференциалах функции)
равны именно тем приращениям
![]() и
и
![]() независимых переменных, которые и
породили приращение функции, стоящее
в левой части формулы.
независимых переменных, которые и
породили приращение функции, стоящее
в левой части формулы.
Легко теперь получить и записать формулу Тейлора (в дифференциальной форме) для функции любого количества независимых переменных.
Хотя в дифференциальной форме формула Тейлора (17) для случая функции многих переменных выглядит так же просто, как и для случая функции одной переменной, в развернутом виде она гораздо сложнее. Вот как выглядят первые три ее члена для функции двух переменных:

В частном
случае, при
![]() и
и
![]() ,
из формулы Тейлора получаем формулу
Маклорена:
,
из формулы Тейлора получаем формулу
Маклорена:
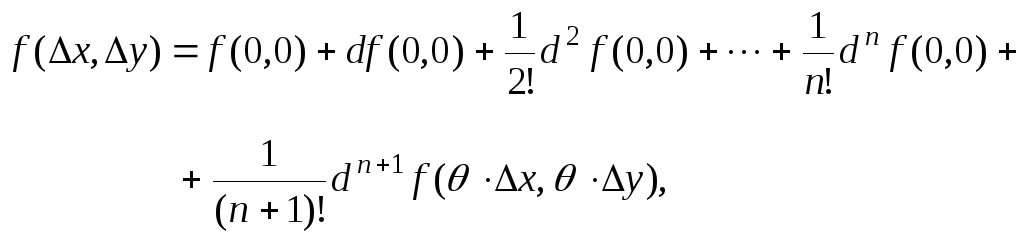
![]() ,
,
или, т.к. тогда
![]() ,
а
,
а
![]() ,
,
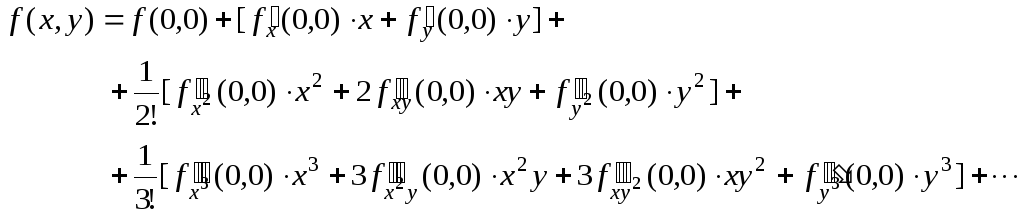
Приведем несколько примеров разложения функций по формуле Тейлора (в данном случае – Маклорена):
1.
![]() ,
,
2.
![]() ,
,
3.
![]() .
.
