
- •I. Первый признак сравнения.
- •II. Второй признак сравнения (признак сравнения в предельной форме).
- •Интегральный признак Коши-Маклорена.
- •Достаточный признак разложимости функции в ряд Тейлора.
- •Приложения степенных рядов.
- •Второй способ решения дифференциального уравнения.
- •III. Применение степенных рядов для приближенного вычисления значений функций.
- •Связь комплексной формы ряда Фурье с комплексным гармоническим колебанием.
- •Спектральные характеристики комплексной формы ряда Фурье.
- •Понятие интеграла от фкп.
- •Ряд Лорана.
Числовые ряды.
Рассмотрим
числовую последовательность
 и для нее введем понятие числового ряда.
и для нее введем понятие числового ряда.
Опр.: Числовым
рядом
 называется аналитическое выражение
вида
называется аналитическое выражение
вида

Опр.:
Частичной суммой числового ряда (n-ой
частичной суммой) называется сумма n
первых слагаемых этого ряда, т.е.

Опр.: Числовой
ряд
 называется сходящимся, если существует
и конечен предел последовательности
частичных сумм этого ряда, т.е.
называется сходящимся, если существует
и конечен предел последовательности
частичных сумм этого ряда, т.е.
 (
( -
const), при этом
-
const), при этом
 называется суммой ряда.
называется суммой ряда.
Опр.: Числовой ряд называется расходящимся, если предел последовательности частичных сумм не существует или обращается в бесконечность.
Необходимый признак сходимости числового ряда.
Теорема:
Для того, чтобы числовой ряд
 сходился, необходимо, чтобы общий член
ряда стремился к нулю.
сходился, необходимо, чтобы общий член
ряда стремился к нулю.
Доказательство:
Дано: ряд сходится.
Доказать:
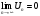
Рассмотрим
две числовых последовательности
 и
и
 .
В силу того, что ряд сходится
.
В силу того, что ряд сходится
 ,
,
 .
Тогда
.
Тогда



Перейдем к пределу:

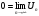
Замечание:
Теорема носит необходимый, но не
достаточный характер, т.е. если общий
член ряда стремится к нулю, то сам ряд
может как сходиться, так и расходиться.
В дальнейшем покажем, что гармонический
ряд
 расходится, хотя
расходится, хотя
 .
.
Достаточный признак расходимости числового ряда.
Теорема:
Для того, чтобы числовой ряд
 расходился, достаточно, чтобы общий
член ряда не стремился к нулю.
расходился, достаточно, чтобы общий
член ряда не стремился к нулю.
Доказательство:
Дано:

Доказать:
 расходится.
расходится.
Проведем методом от противного.
Предположим
противное тому, что нужно доказать, т.е.
пусть ряд
 сходится. В силу доказанного необходимого
признака имеем
сходится. В силу доказанного необходимого
признака имеем
 .
Получаем противоречие с «дано»
.
Получаем противоречие с «дано»
 наше предположение было ложно и ряд
расходится.
наше предположение было ложно и ряд
расходится.
Критерий Коши сходимости числового ряда.
(Необходимое и достаточное условие сходимости числового ряда).
Теорема:
Для того, чтобы числовой ряд
 сходился, необходимо и достаточно, чтобы
сходился, необходимо и достаточно, чтобы

Доказательство:
Воспользуемся
материалом I-го курса: для
того, чтобы последовательность сходилась,
необходимо и достаточно, чтобы она была
фундаментальна (критерий Коши). Запишем
определение фундаментальной
последовательности для


Возьмем в
качестве
 ,
где
,
где
 ,
тогда
,
тогда


Вывод:
 критерий Коши равносилен определению
фундаментальности последовательности
частичных сумм ряда, а всякая фундаментальная
последовательность сходится. Тогда
критерий Коши равносилен определению
фундаментальности последовательности
частичных сумм ряда, а всякая фундаментальная
последовательность сходится. Тогда

 ряд сходится.
ряд сходится.
Доказательство расходимости гармонического ряда с помощью критерия Коши.
Опр.:
Гармоническим рядом называется числовой
ряд вида
 .
.
Покажем,
что для гармонического ряда критерий
Коши не выполняется
 он расходится.
он расходится.
Возьмем в критерии Коши:
 .
.
Оценим:

Критерий
Коши не выполняется
 ряд расходится.
ряд расходится.
Понятие ряда остаточных членов (остатка ряда).
Опр.: Остатком
ряда
 называется числовой ряд вида
называется числовой ряд вида
 .
.
Замечание: Очевидно, что остаток ряда и сам ряд связаны через частичную сумму.
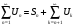
Теорема: Относительно сходимости числовой ряд и его остаток ведут себя одинаково. Либо оба сходятся, либо оба расходятся.
Докажем эту теорему для сходимости (для расходимости доказать самостоятельно).
Дано: ряд
сходится

Доказать:
остаток сходится

Рассмотрим
 - частичную сумму исходящего ряда,
содержащую
- частичную сумму исходящего ряда,
содержащую
 слагаемых.
слагаемых.


Переходя
к пределу при
 ,
,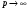 имеем
имеем
 ,
т.к. предел последовательности частичных
сумм остатка существует и конечен (равен
нулю), то остаток является сходящимся
рядом, причем его сумма равна нулю.
,
т.к. предел последовательности частичных
сумм остатка существует и конечен (равен
нулю), то остаток является сходящимся
рядом, причем его сумма равна нулю.
Замечание:


Основные действия над числовыми рядами.
1. Сложение и вычитание рядов.

2. Умножение ряда на число


3. Умножение двух числовых рядов.

Свойства сходящихся рядов.
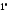 .
Если два числовых ряда сходятся и их
суммы соответственно равны
.
Если два числовых ряда сходятся и их
суммы соответственно равны
 и
и
 ,
то ряд являющийся суммой этих рядов
также сходится и его сумма равна
,
то ряд являющийся суммой этих рядов
также сходится и его сумма равна
 .
.
Дано:
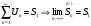
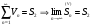
Доказать:
 сходится и его сумма равна
сходится и его сумма равна
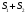 .
.
Доказательство:
Рассмотрим
n-ую частичную сумму ряда
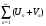

Перегруппируем слагаемые в частичной сумме, т.к. их количество конечно. Имеем:

Переходя
к пределу при
 имеем:
имеем:
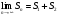 .
.
Замечание: Аналогичное свойство имеет место для разности двух рядов.
 .
Если числовой ряд
.
Если числовой ряд
 сходится и его сумма равна S,
то ряд
сходится и его сумма равна S,
то ряд
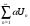 (
( )
– также сходится и его сумма равна
)
– также сходится и его сумма равна
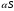 .
.
Доказательство аналогично свойству 1.
 .
Если числовой ряд сходится, то члены
ряда можно, не переставляя их, группировать
произвольно, причем полученный ряд
будет сходится и его сумма не изменится.
.
Если числовой ряд сходится, то члены
ряда можно, не переставляя их, группировать
произвольно, причем полученный ряд
будет сходится и его сумма не изменится.
 .
Если из сходящегося ряда выбросить
определенное число его произвольных
членов, то полученный ряд также будет
сходиться, а его сумма по сравнению с
суммой исходящего ряда изменится на
сумму выброшенных членов.
.
Если из сходящегося ряда выбросить
определенное число его произвольных
членов, то полученный ряд также будет
сходиться, а его сумма по сравнению с
суммой исходящего ряда изменится на
сумму выброшенных членов.
Знакопостоянные числовые ряды.
Опр.: Числовой
ряд
 называется знакопостоянным, если все
его члены либо неположительны
называется знакопостоянным, если все
его члены либо неположительны
 ,
либо неотрицательны
,
либо неотрицательны
 .
.
Замечание:
Знакопостоянный числовые ряды
 принято называть рядами с неотрицательными
членами, а ряды
принято называть рядами с неотрицательными
членами, а ряды
 называются положительными числовыми
рядами. Иногда ряды с неотрицательными
членами также называют положительными.
называются положительными числовыми
рядами. Иногда ряды с неотрицательными
членами также называют положительными.
Поскольку
из ряда
 можно получить положительный ряд,
умножив его на (-1), то на сходимость
исследуют только положительные ряды,
т.к. умножение на константу не влияет
на сходимость.
можно получить положительный ряд,
умножив его на (-1), то на сходимость
исследуют только положительные ряды,
т.к. умножение на константу не влияет
на сходимость.
Критерий сходимости для рядов с неотрицательными членами.
Теорема:
Для того, чтобы числовой ряд
 сходился, необходимо и достаточно, чтобы
последовательность его частичных сумм
была ограничена.
сходился, необходимо и достаточно, чтобы
последовательность его частичных сумм
была ограничена.
 Необходимость:
Необходимость:
Дано:
 сходится
сходится
Доказать:
 - ограниченная
- ограниченная
Доказательство:
Т.к. ряд
сходится
 последовательность
последовательность
 сходится. Из I-го курса
известно, что всякая сходящаяся
последовательность обязательно
ограничена.
сходится. Из I-го курса
известно, что всякая сходящаяся
последовательность обязательно
ограничена.
 Достаточность:
Достаточность:
Дано:
 - ограниченная,
- ограниченная,

Доказать:
 сходится
сходится
Доказательство:
Рассмотрим частичные суммы.


 ,
,
т.е.
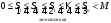 (ограничена)
(ограничена)
В силу
критерия Вейерштрасса, т.к. последовательность
монотонна и ограничена, она сходится,
т.е.
 ряд
сходится.
ряд
сходится.
Признаки сравнения для знакопостоянных рядов.
I. Первый признак сравнения.
Теорема:
Если для двух рядов с неотрицательными
членами
 и
и
 выполняется одно из условий:
выполняется одно из условий:

то в случае
сходимости ряда
 и выполнении условия 1 ряд
и выполнении условия 1 ряд
 сходится,
а в случае расходимости ряда
сходится,
а в случае расходимости ряда
 и выполнения условия 2 ряд
и выполнения условия 2 ряд
 расходится.
расходится.
Докажем первую часть теоремы.
Дано:
 сходится,
сходится,

Доказать:
 сходится.
сходится.
Доказательство:
Рассмотрим
последовательность частичных сумм
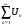 .
Имеем
.
Имеем


Т.к. ряд
 сходится
сходится




 последовательность частичных сумм
последовательность частичных сумм
 ограничена. Кроме того она монотонна.
ограничена. Кроме того она монотонна.
 и т.д.
и т.д.
Т.к. последовательность ограничена и монотонна, она обязательно сходится, т.е.

 -
сходится.
-
сходится.
Докажем вторую часть теоремы.
Доказательство проведем методом от противного.
Дано:
 расходится
расходится

Доказать:
 расходится.
расходится.
Доказательство:
Предположим
противное тому, что нужно доказать, т.е.
ряд
 сходится. Тогда из
сходится. Тогда из
 и первой части теоремы имеем
и первой части теоремы имеем
 сходится.
Получили противоречие с «дано»
сходится.
Получили противоречие с «дано»
 наше предположение было ложным и ряд
наше предположение было ложным и ряд
 расходится.
расходится.
II. Второй признак сравнения (признак сравнения в предельной форме).
Теорема:
Если для двух знакопостоянных рядов
 и
и
 существует и конечен предел
существует и конечен предел
 ,
,
 ,
то относительно сходимости оба ряда
ведут себя одинаково, т.е. либо оба
сходятся, либо оба расходятся.
,
то относительно сходимости оба ряда
ведут себя одинаково, т.е. либо оба
сходятся, либо оба расходятся.
Доказательство:
Воспользуемся определением предела числовой последовательности на языке кванторов:


Пусть
 сходится.
Покажем, что
сходится.
Покажем, что
 также
сходится. Воспользуемся правой частью
неравенства (1).
также
сходится. Воспользуемся правой частью
неравенства (1).



Имеем
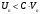
Рассмотрим
 -
положительный ряд.
-
положительный ряд.
В силу I-го
признака сравнения ряд
 сходится.
сходится.
Пусть
 расходится. Докажем, что
расходится. Докажем, что
 расходится. Воспользуемся первой частью
неравенства (1).
расходится. Воспользуемся первой частью
неравенства (1).


Обозначим
 .
В силу произвольности
.
В силу произвольности
 ,
его можно выбрать столь малым, что
,
его можно выбрать столь малым, что
 .
Тогда
.
Тогда

 - положительный ряд, расходится. В силу
I-го признака сравнения
- положительный ряд, расходится. В силу
I-го признака сравнения
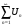 расходится.
расходится.
Признак Даламбера в непредельной форме.
Теорема:
Если для положительного числового ряда
 выполняется одно из условий:
выполняется одно из условий:

то в случае выполнения условия 1 – ряд сходится, а в случае выполнения условия 2 – ряд расходится.
Доказательство:
Докажем первую часть теоремы.



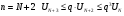 и т.д.
и т.д.
Очевидно,
что

 бесконечно убывающая геометрическая
прогрессия (сходится).
бесконечно убывающая геометрическая
прогрессия (сходится).
В силу I-го
признака сравнения
 сходится.
сходится.

 Ряд
Ряд
 сходится, т.к. отличается на конечное
число слагаемых.
сходится, т.к. отличается на конечное
число слагаемых.
Докажем вторую часть теоремы.



 расходится в силу достаточного признака
расходимости числового ряда.
расходится в силу достаточного признака
расходимости числового ряда.
Признак Даламбера в предельной форме.
Теорема:
Если для положительного числового ряда
 существует конечный или бесконечный
предел
существует конечный или бесконечный
предел
 тогда
тогда
1) если
 ряд сходится
ряд сходится
2) если
 ряд расходится
ряд расходится
3)
 нужны дополнительные исследования.
нужны дополнительные исследования.
Доказательство:
Воспользуемся определением предела числовой последовательности на языке кванторов

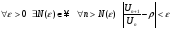
 (2)
(2)
Пусть
 .
Докажем, что ряд сходится. Воспользуемся
правой частью (2).
.
Докажем, что ряд сходится. Воспользуемся
правой частью (2).

 ,
,
 ,
,

Обозначим
 .
В силу произвольности
.
В силу произвольности
 его можно выбрать столь малым, что
его можно выбрать столь малым, что
 .
Тогда
.
Тогда
 .
.
Получили
первое условие признака Даламбера в
непредельной форме ряд сходится.
ряд сходится.
Докажем
вторую часть теоремы:

Воспользуемся левой частью (2)

В силу
произвольности
 его можно выбрать таким, что
его можно выбрать таким, что
 .
.
Тогда
 .
Получили второе условие признака
Даламбера в непредельной форме
.
Получили второе условие признака
Даламбера в непредельной форме ряд расходится.
ряд расходится.
Радикальный признак Коши в непредельной форме.
Теорема:
Если для ряда с неотрицательными членами
 выполняется
одно из условий:
выполняется
одно из условий:

то в случае выполнения условия 1 ряд сходится, а условия 2 – ряд расходится.
Доказательство:
Докажем первую часть теоремы.
 (Б.У.Г.П.
сходится)
(Б.У.Г.П.
сходится)
В силу I-го признака сравнения
 сходится
сходится
 также сходится, т.к. отличается на
конечное число слагаемых.
также сходится, т.к. отличается на
конечное число слагаемых.
Докажем вторую часть теоремы.

 расходится.
расходится.
Радикальный признак Коши в предельной форме.
Теорема:
Если для ряда с неотрицательными членами
 существует конечный или бесконечный
предел
существует конечный или бесконечный
предел

1) если
 -
ряд сходится
-
ряд сходится
2) если
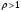 -
ряд расходится
-
ряд расходится
3)
 нужны
дополнительные исследования.
нужны
дополнительные исследования.
Доказательство:
Воспользуемся определением предела числовой последовательности на языке кванторов.


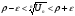 (3)
(3)
Пусть
 .
Докажем, что ряд сходится.
.
Докажем, что ряд сходится.
Воспользуемся правой частью (3)
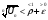 ,
,

В силу
произвольности
 выберем
его столь малым, что
выберем
его столь малым, что

Получили
первое условие радикального признака
в непредельной форме
 ряд сходится.
ряд сходится.
Пусть
 .
Докажем, что ряд расходится. Воспользуемся
левой частью (3)
.
Докажем, что ряд расходится. Воспользуемся
левой частью (3)

Выберем
 таким, что
таким, что


Получили
второе условие радикального признака
 ряд
расходится.
ряд
расходится.
