
- •I. Первый признак сравнения.
- •II. Второй признак сравнения (признак сравнения в предельной форме).
- •Интегральный признак Коши-Маклорена.
- •Достаточный признак разложимости функции в ряд Тейлора.
- •Приложения степенных рядов.
- •Второй способ решения дифференциального уравнения.
- •III. Применение степенных рядов для приближенного вычисления значений функций.
- •Связь комплексной формы ряда Фурье с комплексным гармоническим колебанием.
- •Спектральные характеристики комплексной формы ряда Фурье.
- •Понятие интеграла от фкп.
- •Ряд Лорана.
Второй способ решения дифференциального уравнения.
Решение будем искать в виде:

 :
:




Следовательно, решение имеет вид:

 и
и
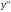 подставим в исходное уравнение
подставим в исходное уравнение




Применим
метод сравнения коэффициентов при
одинаковых степенях
 .
.

Ответ:
 +...
+...

III. Применение степенных рядов для приближенного вычисления значений функций.
Если при приближенном вычислении значений функций получаются знакочередующиеся ряды, то погрешность оценивается с помощью признака Лейбница и по абсолютной величине не превосходит первого из отобранных членов. Если получится знакопостоянный ряд, то погрешность оценивается с помощью геометрической прогрессии.



 -
погрешность вычислений, т.е. до 2-го знака
после запятой.
-
погрешность вычислений, т.е. до 2-го знака
после запятой.

 ,
,
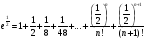 ,
,

Оценим сумму остатка ряда исп-ся сумму геометрической прогрессии




Из данного
неравенства найдем первое значение
 ,
которое ему удовлетворяет:
,
которое ему удовлетворяет:






Приближенное вычисление значений корней.

Приближенное вычисление интегралов.
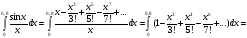

Ряды Фурье.
Опр.: Функция
 ,
заданная на всей числовой оси называется
периодической с периодом Т, если
,
заданная на всей числовой оси называется
периодической с периодом Т, если
 выполняется условие
выполняется условие
 .
.
Опр.: Наименьший положительный период периодической функции называется основным периодом этой функции.
Свойства интеграла для периодической функции.
Теорема: Интегралы по отрезку, равному по длине периоду от периодической функции равны по своему значению, т.е.
 если
если
 .
.
Доказательство:
Оно следует из геометрического смысла определенного интеграла как площади криволинейной трапеции.
Замечание:
Исходя из этого свойства можно в
дальнейшем вместо
 от периодической функции вычислить
от периодической функции вычислить
 .
.
Понятие бесконечной системы тригонометрических функций.
Опр.: Бесконечной системой тригонометрических функций называется совокупность функций вида:

Свойства бесконечной системы тригонометрических функций.
Свойство 1. (Общий период)
Бесконечная
система тригонометрических функций
имеет общий период

Доказательство:

Любую
постоянную функцию можно рассматривать
как периодическую с произвольным
периодом Т. Рассмотрим функцию
 .
Эта функция является периодической с
периодом
.
Эта функция является периодической с
периодом

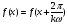

Аналогично для синуса.
Следовательно,
т.к. число
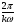
 является периодом бесконечной системы
функций, то и
является периодом бесконечной системы
функций, то и
 также является периодом.
также является периодом.
Свойство 2. (Ортогональности)
Теорема:
Интеграл по отрезку равному по длине
периоду
 от произведения двух разноименных
функций системы равен нулю, т.е.
от произведения двух разноименных
функций системы равен нулю, т.е.


 ,
,


Доказательство:
Проведем
для интегралов
 в силу свойства равенства интегралов
по отрезку, равному по длине периоду.
в силу свойства равенства интегралов
по отрезку, равному по длине периоду.






Свойство 3. (Отличие от нуля интеграла от произведения одноименных функций).
Теорема: Интеграл по отрезку, равному по длине периоду от произведения двух одноименных функций тригонометрической системы отличен от нуля, причем



Доказательство:


Понятие тригонометрического многочлена в вещественной форме.
Опр.: Тригонометрическим многочленом n-го порядка в вещественной форме называется линейная комбинация функций тригонометрической системы вида
 ,
где
,
где
 -коэффициенты
триг.многочлена
-коэффициенты
триг.многочлена
Тригонометрический многочлен в комплексной форме.
Преобразуем тригонометрический многочлен в вещественной форме, используя формулы Эйлера

Имеем
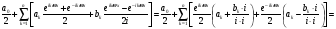

Введем вспомогательные обозначения.



 (*)
(*)
С учетом введенных обозначений тригонометрический многочлен принимает вид:
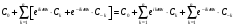
Индекс суммирования сменим во второй сумме

 тогда тригонометр. многочлен принимает
вид:
тогда тригонометр. многочлен принимает
вид:

Вывод: Тригонометрический многочлен в комплексной форме имеет вид
 ,
где
,
где
 - комплексные числа, выражающиеся через
коэффициенты тригонометрического
многочлена в вещественной форме. (*)
- комплексные числа, выражающиеся через
коэффициенты тригонометрического
многочлена в вещественной форме. (*)
Понятие круговой частоты т частоты, измеренной в Гц.
Опр.:
Изменение функции
 за период Т называется ее колебанием.
за период Т называется ее колебанием.
Опр.: Величина
 называется круговой частотой периодической
функции с периодом Т и определяет число
колебаний за
называется круговой частотой периодической
функции с периодом Т и определяет число
колебаний за
 секунд.
секунд.
Опр.: Величина
 называется частотой, измеренной в Гц и
характеризует число колебаний функции
в 1 секунду.
называется частотой, измеренной в Гц и
характеризует число колебаний функции
в 1 секунду.
Замечание:
Очевидна формула

Формулы Эйлера-Фурье.
Теорема:
Если некоторая периодическая функция
с периодом Т представлена в виде
тригонометрического многочлена
 (1)
(1)
то коэффициенты
 (2)
(2)
носят название формул Эйлера-Фурье в вещественной форме.
Доказательство:
Проинтегрируем
(1) по отрезку
 ,
учитывая свойства бесконечной системы
тригонометрических функций.
,
учитывая свойства бесконечной системы
тригонометрических функций.

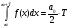

Если умножить
(1) на
 и проинтегрировать по
и проинтегрировать по
 ,
получим формулы для вычисления
,
получим формулы для вычисления
 :
:



Умножим
соотношение (1) на
 и проинтегрируем по отрезку
и проинтегрируем по отрезку
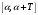 ,
используя свойства бесконечной системы
тригонометрических функций:
,
используя свойства бесконечной системы
тригонометрических функций:



Формулы Эйлера-Фурье в комплексной форме.
Ранее были получены две формы записи тригонометрического многочлена и формулы связи между ними.


Подставим
формулы Эйлера-Фурье, найденный для
вещественной формы, в коэффициент
 .
.


Учитывая,
что

Получаем
аналогичную формулу для


Очевидно,

Сделаем
замену индекса у коэффициентов с
отрицательными индексами. Обозначим



С учетом введенной замены получаем единую формулу

Понятие ряда Фурье в вещественной и комплексной формах.
Опр.1: Рядом
Фурье в вещественной форме для
периодической функции
 с периодом Т называется тригонометрический
ряд вида:
с периодом Т называется тригонометрический
ряд вида:
 ,
в котором коэффициенты определяются
по формулам Эйлера-Фурье:
,
в котором коэффициенты определяются
по формулам Эйлера-Фурье:

 -
круговая частота (*)
-
круговая частота (*)
Опр.2: Рядом
Фурье в комплексной форме для периодической
функции
 с
периодом Т называется ряд вида:
с
периодом Т называется ряд вида:
 ,
в котором коэффициенты определяются
по формулам Эйлера-Фурье:
,
в котором коэффициенты определяются
по формулам Эйлера-Фурье:
 (**)
(**)
Замечание:
Ряды Фурье (*) и (**) построенные для
периодической функции
 могут:
могут:
1) расходиться
для

2) сходиться
в искомой области
 к искомой функции
к искомой функции

3) сходиться
на всей числовой оси к функции

В третьем
случае говорят, что функция разложена
в ряд Фурье и вместо « »
пишут «=».
»
пишут «=».
Условие Дирихле.
Если
 на некотором отрезке
на некотором отрезке
 удовлетворяет двум условиям:
удовлетворяет двум условиям:
1)
 - непрерывна на этом отрезке, либо имеет
на нем конечное число точек разрыва
I-го рода.
- непрерывна на этом отрезке, либо имеет
на нем конечное число точек разрыва
I-го рода.
2)
 монотонна на этом отрезке , либо имеет
на нем конечное число экстремумов, то
говорят, что функция
монотонна на этом отрезке , либо имеет
на нем конечное число экстремумов, то
говорят, что функция
 удовлетворяет условиям Дирихле.
удовлетворяет условиям Дирихле.
Замечание: из определения функции, удовлетворяющей условиям Дирихле ясно, что эту функцию можно разбить на части (область определения – конечные отрезки), на которых функция непрерывна и монотонна.
Теорема Дирихле (необходимое и достаточное условие разложимости функции в ряд Фурье)
Теорема:
Если функция
 на некотором конечном отрезке
на некотором конечном отрезке
 удовлетворяет условиям Дирихле, то она
разложена на этом отрезке в ряд Фурье,
причем в каждой точке непрерывности
функций сумма ряда Фурье совпадает со
значением функции в точке
удовлетворяет условиям Дирихле, то она
разложена на этом отрезке в ряд Фурье,
причем в каждой точке непрерывности
функций сумма ряда Фурье совпадает со
значением функции в точке
 ,
а в каждой точке разрыва I-го
рода
,
а в каждой точке разрыва I-го
рода

(без доказательства)
Связь вещественной формы ряда Фурье с гармоническими колебаниями.
Преобразуем ряд Фурье (*) к виду:
 (3)
(3)
Теорема:
 такой, что
такой, что
 ,
,
 ,
этот угол представляет собой угол,
отсчитывающий от оси Ох (в положительном
или отрицательном направлении) до луча,
соединяющего начало координат с точкой
,
этот угол представляет собой угол,
отсчитывающий от оси Ох (в положительном
или отрицательном направлении) до луча,
соединяющего начало координат с точкой
 ,
причем
,
причем
 и находится по формуле
и находится по формуле

Доказательство:
1)
 (как тангенс угла в прямоугольном
треугольнике)
(как тангенс угла в прямоугольном
треугольнике)
 катеты в прямоуг.треугольнике
катеты в прямоуг.треугольнике

Случай I четверти доказан
2)
 =
=









Случай II четверти доказан.
С учетом теоремы запишем соотношение (3)
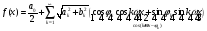
Введем вспомогательное обозначение

 ,
тогда ряд Фурье принимает вид
,
тогда ряд Фурье принимает вид
 (4)
(4)
Вывод: Ряд
Фурье, записанный в виде (4) представляет
собой сумму гармоник с амплитудами
 ,
круговыми частотами
,
круговыми частотами
 и фазами
и фазами
 .
.
Выражение коэффициентов в вещественной форме ряда Фурье через амплитуды и фазы.
 ,
,



Спектральные характеристики вещественной формы ряда Фурье.
Выделяют 4 основных спектральных характеристик вещественной формы ряда Фурье:
1) частотные спектры
2) линейчатые спектры
3) амплитудно-частотный спектр
4) фазово-частотный спектр
I. Частотные спектры.
Опр.:
Частотные спектры вещественной формы
ряда Фурье называют числовые
последовательности
 и
и





Замечание: Частотные спектры можно рассматривать как масштабную линейку.
II. Линейчатые спектры.
Опр.:
Линейчатые спектры вещественной формы
ряда Фурье называют числовые
последовательности
 ,
,

III. АЧХ.
Опр.:
Амплитудно-частотным спектром вещественной
формы ряда Фурье называют числовую
последовательность


График АЧХ может находиться только в I четверти координатной плоскости.
IV. ФЧХ.
Опр.:
Фазово-частотным спектром вещественной
формы ряда Фурье называют числовую
последовательность
 ,
,
 ,
если
,
если
 четв.,
четв.,
 ,
если
,
если

 ,
если
,
если





