
Курс лекций / 04
.pdf
Доцент Петров В.В. Лекции по Геодезии. Лекция 4. Дата печати 09.03.2003 19:54 стр. 1 из 6
3.Линейно-угловые измерения
3.1.Понятия об измерениях и ошибках измерений
При выполнении геодезических работ измеряют различные величины: горизонтальные и вертикальные углы, расстояния, превышения, температуру и давление воздуха и т.д. Измерить некоторую величину X означает сравнить ее с однородной ей величиной E (единицей меры). В результате измерения устанавливают, сколько раз единица меры содержится в измеряемой величине. Различают измерения непосредственные (прямые) и посредственные (косвенные). В первом случае искомая величина непосредственно сравнивается с единицей меры (например, измерение вместимости ведра с помощью воды и литровой банки). Во втором измеряется некоторая другая величина, которая связана с искомой - функциональной зависимостью (определение вместимости того же ведра путем измерения его высоты и диаметров).
В процессе измерений обязательно возникают ошибки. По характеру действия они бывают грубые, случайные и систематические. Грубые ошибки возникают вследствие невнимательности исполнителя, неблагоприятных условий или непродуманной методики выполнения работ. Такие ошибки стараются исключить, и эффективным средством для этого являются повторные измерения.
Систематические ошибки подчиняются определенным закономерностям. Источниками их возникновения являются: несовершенство приборов, изменение внешних условий выполнения работ и влияние различных факторов на действия исполнителя. Поэтому они подразделяются на ошибки приборные, внешней среды и личные ошибки наблюдателя. Закономерности, которым подчиняются систематические ошибки, изучают, и это позволят их исключить из результатов измерений (например, определяют температурный коэффициент расширения стали для введения поправок в расстояния измеренные стальной рулеткой).
Случайные ошибки возникают из-за воздействия на процесс измерений огромного числа непрерывно меняющихся факторов, учесть, а значит, и исключить влияние которых на результат невозможно. Но возникающие при этом ошибки подчиняются определенным закономерностям, проявляющимся тем ярче, чем более массовый характер носят сами измерения. Указанные закономерности называются статистическими и являются предметом изучения таких наук, как теория вероятности и математическая статистика.
Пусть l – результат измерения некоторой величины X, истинное значение которой обозначим буквой L. Тогда разность ∆=l–L и называется случайной ошибкой измерения. Ее также называют истинной ошибкой, как отклонение результата измерений от истинного значения измеряемой величины, и, кроме того, абсолютной ошибкой в отличие от дроби ∆/L, которую называют относительной ошибкой измерений. В процессе массовых измерений случайные ошибки подчиняются следующим закономерностям:
При постоянных условиях измерений (т.е. при равноточных измерениях) ошибки по абсолютной величине не могут превосходить некоторого предела;
Равные по абсолютной величине положительные и отрицательные ошибки – равновероятны; Малые по абсолютной величине ошибки встречаются чаще, чем большие;
Среднее арифметическое из случайных ошибок равноточных измерений стремится к нулю, когда число измерений n стремится к бесконечности, т.е.
lim [∆n] → 0 , если n→∞
Значок [∆] равносилен выражению ∑∆ и называется гауссовой суммой. Из выше приведенных рассуждений следует, что сама случайная
ошибка не может служить критерием точности измерений. К.Ф. Гаусс предложил в качестве такого критерия использовать среднюю квадратическую ошибку m, вычисляемую по формуле:
m = [∆2 ] n |
(14) |
|
Преимущество средней квадратической ошибки в том, что она стандартна для ряда равноточных измерений (кстати, в статистике стандартом и называется) и имеет следующий вероятностный смысл.
Пусть l – результат измерений. Каковы вероятности того, что истинная величина L [l + m,l − m], или [l + 2m,l − 2m], или
[l + 3m,l − 3m]? Теория утверждает, что эти вероятности соответственно равны 68, 95 и 99.7%. Но это означает, что появление ошибок
превышающих 3m маловероятно. Указанное обстоятельство позволило принять эту величину в качестве предельной ошибки, и использовать для выявления грубых погрешностей. Иногда в качестве предельной используют удвоенную среднюю квадратическую ошибку.
При выполнении косвенных измерений, когда искомая величина Y является функцией измеренной величины X, ошибка результата оценивается по формуле:
|
|
|
|
|
|
|
|
|
|
|
my |
= ϕ |
′ |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
(x)mx |
|
|
|
|
|
(15) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А если она является функцией нескольких переменных X1 , X 2 ,...X n , то используют соотношение: |
|
||||||||||||||||||||||
|
2 |
|
|
∂Y |
|
2 |
|
2 |
|
|
∂Y |
|
2 |
|
2 |
|
∂Y |
|
2 |
|
2 |
(16) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
m |
= |
|
m |
|
|
+ |
|
m |
|
|
|
m |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
y |
|
|
∂X1 |
|
X1 |
|
|
|
|
∂X 2 |
|
X 2 |
|
|
|
∂X n |
|
X n |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
На практике в подавляющем числе случаев истинное значение измеряемой величины неизвестно и перед исполнителем, выполнившим несколько ее измерений, возникают следующие три вопроса: что принять за результат измерений, каковы средняя квадратическая ошибки одного измерения и ошибка результата. Для того чтобы ответить на поставленные вопросы предположим, что выполнено n изме-
Доцент Петров В.В. Лекции по Геодезии. Лекция 4. Дата печати 09.03.2003 19:54 стр. 1 из 6
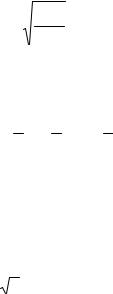
Доцент Петров В.В. Лекции по Геодезии. Лекция 4. Дата печати 09.03.2003 19:54 стр. 2 из 6
рений одной и той же известной величины и получено столько же истинных ошибок ∆i = li − L . Сложим, левые и правые части равенства, разделим их на число измерений и перейдем к пределам, в результате получим:
lim |
[∆] |
= lim [l] |
+ lim |
nL |
|
n |
|
|
|||
n→∞ |
n→∞ n |
n→∞ n |
|||
Левая часть выше приведенного соотношения по 4 свойству случайных ошибок измерений стремиться к нулю, первое слагаемое правой части (обозначим буквой L0 ) является средним из всех измерений, а второе слагаемое равно L. Таким образом, получается, что среднее
стремится к истинному значению измеряемой величины при увеличении числа измерений до бесконечности, и есть все основания принимать его за результат измерений и определяемой величины.
Для вычисления ошибки отдельного измерения используется формула Бесселя:
m = |
[Vi |
2 ] |
|
n −1 |
|
В ней Vi , i=1,2,…n – отклонения отдельных измерений от среднего значения. Причем, если вычисления верны, то сумма отклонений должна равняться нулю.
Для оценки точности результата запишем формулу вычисления среднего в виде:
L0 = 1n l1 + 1n l2 + ... 1n ln ,
и воспользуемся соотношением (16) для вычисления ошибки функции нескольких переменных, в результате получим:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
2 |
||||||||
mL |
1 |
ml |
|
ml |
|
|
ml |
|
|
|
||||||||
= |
|
|
|
+ |
|
|
|
|
+ ... + |
|
|
|
|
|||||
|
|
|
|
|
|
|
||||||||||||
0 |
n |
1 |
|
|
n |
|
2 |
|
|
n |
|
n |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Примем ошибки отдельных измерений равными, т.е. ml1 = ml2 = ... = mln = ml , тогда:
mL |
= ml / n |
(17) |
|
||
0 |
|
|
Таким образом, повторные измерения, не только позволяют исключать грубые ошибки, но и повышают точность результата измерений.
3.2. Линейные измерения
Линейными называют измерения расстояний между точками земной поверхности. Выполнять эту работу приходится при построении опорных геодезических сетей, создании съемочного обоснования и в процессе съемки местности. Для исключения грубых ошибок
одно и то же расстояние измеряют дважды.
Единицей измерения в большинстве стран мира принят метр (от греч. µετρον -мера). Появился он в конце 18 века, после того
как французские ученые предложили в качестве единицы длины принять 10 10−6 часть 1/4 дуги Парижского меридиана. Были выполнены точные градусные измерения, изготовлен архивный метр из платиново-иридиевого сплава, а спустя почти 100 лет и 31 его копия. Две из них достались России. C 1983 года за 1 метр приняли расстояние, которое проходит в вакууме плоская электромагнитная волна за
1/299 792 458 секунды.
К настоящему времени предложено достаточно много, как непосредственных, так и косвенных способов измерения расстояний: шагами (точность 1/100); мерными колесами или дисками (1/500 - 1/20 000); землемерным циркулем (1/1 000); мерными лентами или рулетками (1/2 000 - 1/10 000); оптическими дальномерами (1/300 - 1/5 000); свето и радиодальномерами (до 1/500 000); инварными проволоками (1/1000 000); спутниковыми методами (1/1000 000); на интерференционном компараторе (1:15 000 000).
3.2.1. Приборы для измерения расстояний непосредственным способом
Непосредственный способ состоит в откладывании мерного прибора с известной длиной в створе линии, длину которой требует-
ся определить. Створом называется вертикальная плоскость, проходящая через конечные точки линии. Для измерений используют, пре-
жде всего, рулетки, землемерные ленты и проволоки. Известны случаи измерения расстояний с помощью мерного диска.
Рулетки предназначены для измерения сравнительно коротких отрезков в процессе съемки местности, при обмерах зданий и сооружений, выполнении разбивок на строительных площадках. Их полотно длиной от 1 до 100 м делают из углеродистой или нержавеющей стали, капрона, стекловолокна или из прочной тесьмы, реже - инвара. По точности нанесения шкал рулетки делятся на 3 класса, при этом их цена деления может быть равна 1 мм или 1 см. В топографо-геодезическом производстве в основном используют стальные 10–50 метровые рулетки, а при менее точных работах – тесьмяные, длиной 10 м. По названию рулетки можно судить о ее характеристиках. Например рулетка ОПК2–30АНТ/10 - с открытым корпусом, плоская, имеет вытяжное кольцо, 2 класса точности, 30 метровая, начало шкалы не совпадает с торцом полотна, выполнена из нержавеющей стали, шкала нанесена методом травления, цена деления 10 мм.
Доцент Петров В.В. Лекции по Геодезии. Лекция 4. Дата печати 09.03.2003 19:54 стр. 2 из 6

Доцент Петров В.В. Лекции по Геодезии. Лекция 4. Дата печати 09.03.2003 19:54 стр. 3 из 6
Ленты землемерные выпускают двух типов ЛЗ (штриховые) и ЛЗШ (шкаловые). Лента штриховая представляет собой стальную полосу длиной 20 или 24 м, шириной 15–20 мм и толщиной 0.3–0.4 мм, на концах которой нанесены штрихи, ограничивающие ее длину (Рис. 23). В полотне ленты просверлены отверстия через 10 см. Латунные заклепки фиксируют полуметровые интервалы, а пластины с числами - метровые. Закреплены они на обеих сторонах ленты, но шкалы возрастают в противоположные стороны. Лента наматывается на кольцо с проушинами. В комплект входят 6 или 11 металлических шпилек. В зависимости от условий местности штриховые ленты обеспечивают точность линейных измерений в пределах от 1/1 000 до 1/ 3 000.
Шкаловые ленты используются для измерений расстояний между точками с повышенной точностью. Они представляют собой сплошную полосу со шкалами на концах длиной по 10 см и ценой деления 1 мм. Разбивка на метровые или более мелкие отрезки между шкалами отсутствует.
Для линейных измерений с высокой точностью применялся базисный прибор БП–2М. В его комплект входят 4 инварные проволоки по 24 м каждая со шкалками на концах, рулетка с инварной лентой длиной 6 или 12 м и вспомогательное оборудование (штативы,
1
100см
20м
Рис.23. Штриховая землемерная лента (показана без ручек)
целики, гири и т.д.). Цена деления шкал 1 мм. Рулетка предназначена для домера остатков измеряемых линий. Долгое время базисный прибор был единственным средством высокоточных линейных измерений в плановых государственных геодезических сетях.
В ряде производственных организаций при измерении расстояний успешно применялся длиномер АД-1М. В комплект прибора входят 2 стальные проволоки длиной до 500 м, которые натягиваются между конечными точками измеряемого отрезка, и измерительная головка, в корпусе которой размещены: мерный диск, счетный механизм, два направляющих ролика и тормозное устройство. В процессе измерения диск прокатывается по проволоке, а счетное устройство по числу оборотов фиксирует расстояние с точностью до 1 мм.
3.2.2. Измерение расстояний штриховыми землемерными лентами
Фактическая длина ленты обычно отличается от номинальной, и необходимо определить насколько велико это различие, для того чтобы вводить поправки в результаты измерений. Сделать это можно до начала работ или сразу после их завершения путем сравнение длины ленты с эталоном - нормальной лентой или отрезком (базисом) соответствующей длины, измеренным с высокой точностью. Процесс сравнения длин мерных приборов с эталоном называется компарированием, а определенная в результате поправка – поправкой за компарирование. Если длина ленты отличается от номинала меньше чем на 1/10 000 ее длины, то поправки не вводятся, в противном случае – вводятся, причем со знаком плюс, когда лента длиннее.
При измерении расстояния лента должна укладываться в створе линии. Отклонение от створа приводит к увеличению измеряемой длины, поэтому если она велика и профиль местности сложен, створ закрепляют рядом вех. Совокупность действий, связанных с их установкой называют вешением линий. Короткие линии (150–200 м) провешивают “на глаз”. Для этого две вешки устанавливаются на конечных точках. Затем наблюдатель становится на одной из них и руководит рабочим, устанавливающим третью вешку так, чтобы все три вешки при визировании перекрывали друг друга. Провешивать линию можно “на себя”(от конца измеряемого отрезка) и ”от себя”. Первый вариант точнее. При больших длинах провешивание линии выполняют с помощью теодолита.
Процесс измерений выполняется двумя рабочими. Задний рабочий, взяв одну шпильку и передав остальные переднему, втыкает ее в точку, обозначающую начало линии, вставляет прорезь ленты расположенную у заднего штриха в шпильку и направляет переднего так, чтобы он уложил ленту в створе. Передний рабочий, встряхнув ленту, натягивает ее с силой примерно 10 кг, прижимает ручку к земле и, вставляя шпильку в прорезь против переднего штриха, втыкает ее в землю. Задний рабочий вытаскивает первую шпильку из земли, и оба передвигаются вдоль линии на длину ленты. Аналогично лента укладывается второй, третий раз и т.д. Когда шпильки заканчиваются, задний рабочий передает переднему 10 штук и процесс измерений продолжается. Как правило, длины линий не кратны длине ленты, которая из-за этого укладывается не целое число раз. В результате образуется остаток (домер). При его измерении отсчет берут с точностью до сантиметра, оценивая десятые дециметра “на глаз “,(предварительно убедившись, что шкала возрастает по ходу движения). Если при измерении используется 20 м. лента, то длина D всей линии равна:
D = 200n1 + 20n2 + d |
(18) |
|
|
||
где n1 , n2 и d – число передач, число шпилек, оказавшихся у заднего рабочего в конце измерения и домер соответственно. |
||
Для контроля обязательно выполняют измерение и в обратном направлении, а полученные результаты сравнивают. Их разность |
||
не должна превышать 1 см на каждую отложенную ленту. |
|
|
Очевидно, что из-за неровностей земной поверхности измеряют наклонные лини, углы наклона которых, как правило, непостоян- |
||
ны. Для последующих вычислений нужны их горизонтальные проекции, поэтому в процессе измерений линию разбивают на отрезки и |
||
определяют угол наклона ν каждого из них, а искомые проекции вы- |
4 |
|
числяют по формуле (2). При измерении длин мерной лентой углы |
||
наклона определяют для каждой 20 метрового отрезка, причем, если |
5 |
|
его величина не превышает 6°, то для этой цели используют экли- |
||
3 |
||
метр. Общее горизонтальное расстояние получают как сумму гори- |
||
зонтальных проекций отрезков. |
6 |
|
В настоящее время на производстве наиболее распространен |
2 |
|
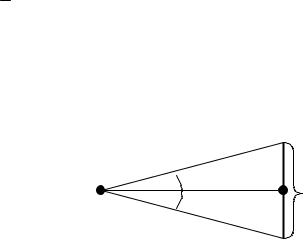
маятниковый эклиметр–высотомер ЭВ-1 (Рис. 24). Он предназначен |
|
|
для измерения углов наклона в пределах ±60° с точностью 0.5°, а так- |
1 |
|
|
||
Доцент Петров В.В. Лекции по Геодезии. Лекция 4. Дата печати 09.03.2003 19:54 стр. 3 из 6 |
||
|
Рис 24. Эклиметр (разрез и вид со стороны лупы) |
|
Доцент Петров В.В. Лекции по Геодезии. Лекция 4. Дата печати 09.03.2003 19:54 стр. 4 из 6
же для измерения высот предметов с расстояний 15 и 20 м, и представляет собой небольшую металлическую коробочку 1 прямоугольной формы, в которой вокруг горизонтальной оси, закрепленной с помощью двух агатовых подпятников, вращается кольцо 2 с грузом 3. На ободе кольца нанесены две шкалы: для измерения углов наклона и для измерения высот предметов. На первой из них по обе стороны от нулевого штриха нанесены градусные деления (цена деления 1°). Под действием груза нулевой диаметр кольца устанавливается горизонтально, если прижата стопорная кнопка 4 (арретир), расположенная сверху коробки. С помощью визирного индекса 6 диафрагмы через лупу 5 берется отсчет. Визирование ведется вдоль наружной вертикальной стенки корпуса путем совмещения индекса с точкой визирования. Прежде чем использовать эклиметр следует определить его место нуля (МО).
Местом нуля шкалы любого прибора называется отсчет по шкале при определенных условиях (например, отсчет по шкале весов,
когда на них нет груза). Искомая величина (вес продукта, например) в этом случае равна отсчету полученному в результате измерений минус МО. Место нуля эклиметра это отсчет по его шкале при условии, что ось визирования горизонтальна. Получить его можно путем наведения индекса на линию горизонта. Если это невозможно, то следует эклиметром выполнить измерение угла наклона одного и того же отрезка прямо и обратно, тогда место нуля будет равно полу сумме полученных отсчетов.
Отметим, что в настоящее время горизонтальные расстояния легко вычислить на компьютере или с помощью калькулятора. Но еще совсем недавно их определяли путем введения поправок, ∆D , которые находили в таблицах. Значения поправок, вычислялись по формуле:
∆D = 2DSin2 (ν / 2) |
(19) |
Получить эту формулу легко, с помощью следующих преобразований:
∆D = D − L = D − DCosν = D(1 − Cosν ) = 2DSin2 (ν / 2)
3.2.3. Принципы измерения расстояний дальномерами
Дальномеры это приборы для определения расстояний между точками. По принципам действия их можно разделить на две группы: оптические дальномеры; свето и радиодальномеры.
В основу определения расстояний оптическими дальномерами, например между точками A и E ,положено решение равнобедренного треугольника ABC (Рис.25). Искомая величина - его высота, поэтому:
L = 12 bCtg ϕ2
Угол ϕ называется параллактическим, а отрезок BC – базисом. В конструкциях дальномеров предусматривается, что одна из величин правой части формулы является постоянной, а вторая переменной, которая и измеряется. Таким образом, существует два типа оптических дальномеров: дальномеры с постоянным параллактическим углом и дальномеры с постоянным базисом. Типичный представитель первого
– нитяной дальномер. Им снабжены зрительные трубы, практически, всех геодезических приборов. Представитель второго типа – рейка Bala, длина базиса которой 2 м. Если параллактический угол измерять с ошибкой 1″-2″, то точность определения расстояния c помощью рейки сопоставима с точностью его измерения мерной лентой.
В свето и радиодальномерах тем или иным способом определяются: либо время, τ, за которое электромагнитная волна проходит расстояние между точками, либо число N модулированных колебаний (длин волн λ), которое укладывается между точками. То есть волна играет роль мерной ленты. Поэтому бывают дальномеры импульсного и фазового типов. Перед измерением на одном из концов линии устанавливается приемо-передатчик, а на другом – отражатель. У дальномеров импульсного типа расстояние вычисляется по формуле:
D = Cτ / 2
|
|
|
B |
|
A |
ϕ |
L |
Е |
b |
|
|
С
Рис.25. Схема параллактического треугольника
C – скорость распространения электромагнитной волны, которая зависит от температуры и влажности воздуха, а также от величины атмосферного давления. Поэтому указанные характеристики атмосферы тоже измеряются. Формула для определения расстояний в фазовом дальномере имеет вид:
D = λ(N + ∆N ) / 2
Величина ∆N – разность фаз модулированных колебаний, посланной и отраженной электромагнитных волн. Она и измеряется в дальномерах фазового типа. Нетрудно видеть, что если длина волны дана, то в выше приведенном уравнении две величины N и D - неизвестны. Поэтому, для разрешения многозначности используют волны разной длины.
3.2.4. Устройство зрительных труб геодезических приборов
Зрительная труба является важнейшей частью большинства геодезических приборов. Они бывают астрономическими и земными. Астрономические трубы дают обратное изображение рассматриваемых предметов, земные – их прямое изображение. Зрительные трубы, кроме того, бывают с внутренней фокусировкой и - с внешней.
Доцент Петров В.В. Лекции по Геодезии. Лекция 4. Дата печати 09.03.2003 19:54 стр. 4 из 6
Доцент Петров В.В. Лекции по Геодезии. Лекция 4. |
Дата печати 09.03.2003 19:54 |
стр. 5 из 6 |
|
|
|
||
На Рис.26 показана астрономическая зрительная труба с внешней фокусировкой, являющаяся оптической системой, состоящей из |
|||||||
объектива 7 и окуляра 5. Объектив зрительной трубы строит за своей фокальной плоскостью действительное обратное и уменьшенное |
|||||||
изображение. Построенное изображение рассматривается через окуляр, играющий роль лупы, которая строит его мнимое прямое и увели- |
|||||||
ченное изображение. |
|
|
|
|
|
|
|
Для наведения на визирную цель имеется сетка нитей. В |
|
|
9 |
1 |
2 |
|
|
простейшем случае это стеклянная пластинка 3 в металлической |
|
|
|
3 |
|
||
оправе, на которой нанесены два тонких взаимно перпендикуляр- |
8 |
|
|
|
4 |
||
ных штриха. Юстировочные винты 6 служат для надлежащей |
|
|
|
|
|
|
|
установки сетки в трубе. Линия 8, проходящая через оптический |
|
|
|
|
|
5 |
|
центр объектива и перекрестие сетки, называется визирной |
7 |
|
|
|
|
||
осью зрительной трубы. Сетка нитей должна располагаться в |
|
|
|
|
|
||
|
|
|
|
|
6 |
||
плоскости изображения, построенного объективом. Это достига- |
|
|
|
|
|
||
ется перемещением окулярного колена 2 при вращении кремалье- |
|
|
|
|
|
|
|
ры (фокусирующего винта) 1. Указанная операция называется |
|
Рис.26. Астрономическая зрительная труба |
|||||
наведением трубы по предмету. Вращением окулярного (диоп- |
|
|
|
|
|
|
|
трийного) кольца 4 достигается качественное изображение сетки |
|
|
|
|
|
|
|
и объекта при рассматривании их через окуляр. Эту операцию называют наведением трубы по глазу. Таким образом, при визировании на |
|||||||
цель трубу обязательно наводят по глазу и по предмету. Это повышает точность измерений и устраняет параллакс сетки нитей (сме- |
|||||||
щение перекрестия сетки с изображения наблюдаемой цели при перемещении глаза относительно окуляра). |
|
|
|||||
В настоящее время трубе с внешней фокусировкой предпочитают трубу с внутренней фокусировкой, у которой, для наведения по предмету вместо окулярного колена используется фокусирующая линза 9 (на Рис.26 показана пунктиром). Такая труба компактнее и лучше защищена от воздействия атмосферы.
Основными характеристиками зрительных труб являются их увеличение, поле зрения и яркость изображения. Видимым или уг-
ловым увеличением называют отношение угла, под которым изображение рассматривается в трубу к углу, под которым оно видно не-
вооруженным глазом. Практически увеличение равно отношению фокусных расстояний объектива и окуляра, и находится в пределах 15-
30Χ у технических и 40Χ - у высокоточных приборов. Угол поля зрения у зрительных труб находится в пределах от30′ до 2°. Для увеличения яркости изображения применяют просветленную оптику. Отметим, что увеличение и поле зрения трубы легко оценить с помощью вертикально установленной недалеко от прибора рейки с делениями.
|
3.2.5. Нитяный дальномер |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Нитяный дальномер предназначен для измерения расстояний с помощью дальномерной рейки, весьма прост по устройству и |
||||||||||||||||||||||||||||||||||||||||||
имеется в зрительных трубах большинства |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l′ |
|
|
|
|
|
|
|
||
геодезических приборов. Сетка нитей та- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ких труб имеет две нити l и m, называемые |
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
дальномерными (Рис.27). |
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пусть L - искомое расстояние |
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
между точками A и B на местности. Уста- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
новим над точкой A геодезический прибор, |
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
труба которого имеет дальномерные нити, |
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
а над точкой B – дальномерную рейку с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сантиметровыми делениями. Пусть l′ и m′ - |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m′ |
|
|
|
|
|
|
|
|||
точки на рейке, куда проектируются даль- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
номерные нити при визировании, и рас- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ |
|
|
f |
|
|
|
|
|
|
L′ |
|
|
|
|
|
|
|
|
|
|
||||||||||
стояние между ними - n сантиметровых |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
делений (с точность до десятых деления). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Обозначим отрезок между дальномерными |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
нитями на сетке буквой p. Из рисунка име- |
|
||
ем: |
|
Рис.27. Принцип измерения расстояний нитяным дальномером |
|
L = L′ + |
f + δ |
||
|
|||
Из подобия треугольников Fml и Fm′l′ следует:
L′ = fn / p
Обозначим сумму f+δ через c, она называется постоянной дальномера; а дробь |
f /p – через k, это коэффициент нитяного дальномера. |
В результате получим: |
|
L=kn+c |
(20) |
Отметим, что в зрительных трубах с внутренней фокусировкой постоянная дальномера мала, и ею часто пренебрегают. Фокусное расстояние объектива и отрезок между дальномерными нитями на сетке стараются подобрать так, чтобы коэффициент дальномера был равен 100 или 200, но это не всегда удается, поэтому перед работой следует уточнить его величину. С этой целью на сравнительно ровной площадке в створе примерно через 20 м закрепляют колышки, и мерной лентой измеряют отрезки между ними (они служат эталонами, так как измерения лентой на порядок точнее). Затем на одной из крайних точек устанавливают прибор с нитяным дальномером, а на другие последовательно - дальномерную рейку и измеряют расстояния по нитяному дальномеру несколькими приемами, полагая, что коэффициент дальномера равен 100. Сравнения результаты, полученные мерной лентой и дальномером, составляют таблицу поправок в дальномерные расстояния для отрезков 20, 40, 60 и т.д. метров.
3.2.6. Понятие о дальномерах двойного изображения
Доцент Петров В.В. Лекции по Геодезии. Лекция 4. Дата печати 09.03.2003 19:54 стр. 5 из 6

Доцент Петров В.В. Лекции по Геодезии. Лекция 4. Дата печати 09.03.2003 19:54 стр. 6 из 6
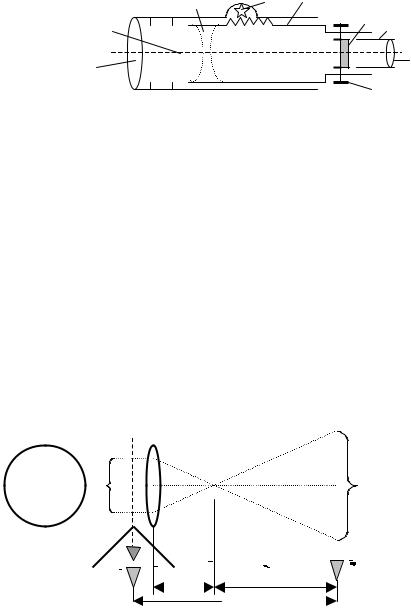
В дальномерах двойного изображения перед объективом зрительной трубы помещается тонкостенная длиннофокусная линза (Рис.28).При совпадении оптической оси этой линзы (она на рисунке изображена пунктиром) c визирной осью трубы изображение точки M рейки в поле зрения совместится с перекрестием m сетки. Если сместить линзу на величину ∆, луч изменит свое направление на угол β и перекрестие сетки будет наведено на точку M′. Для того, чтобы в поле зрения были видны оба изображения (смещенное и несмещенное), перекрывают только половину объектива. Тогда можно, либо измерить величину ∆, имея марки M и M′ на рейке в фиксированном положении (дальномер с постоянным базисом b), либо при постоянном параллактическом угле β определить, насколько сместится марка M, если на рейке есть шкала. Как следует из Рис.28, расстояние между точками A и B равно сумме L′+C, но в первом случае:
L′ = bf / ∆ и L = k / ∆ + C
Во втором:
L′ = bCtgβ и L = kb + C
Дальномеры с переменным параллактическим углом Д2, ДН-8 позволяют измерять расстояния с точностью 1:1 000 – 1: 5 000; с постоянным параллактическим углом с точностью 1:1 000 – 1:2 000. Они выпускались в виде насадок к теодолитам, а использовались как горизонтальные, так и вертикальные рейки.
m |
|
|
M |
∆ |
|
B |
|
A |
β |
||
|
|
b |
|
|
|
|
|
|
C |
f |
M′ |
|
|
|
|
|
|
L |
|
Рис. 28. Схема дальномера двойного изображения |
|
||
Доцент Петров В.В. Лекции по Геодезии. Лекция 4. Дата печати 09.03.2003 19:54 стр. 6 из 6
