
DISKRETKA_ShPORY_end
.doc|
18. Метод математической индукции. В математике при доказательстве утверждений часто используется метод математической индукции. Индукция бывает полной и неполной. Неполная математическая индукция возможно только в том случае, если осуществим полный перебор. Иначе применяют принцип полной математической индукции.
1. база индукции (проверка предположения) Ф(1) – проверяем истинность утверждения при n=1 2. индукционное предположение Ф(к) – предпожим, что утверждение истино при n=k 3. индукционный шаг Ф(к)Ф(к+1). Докажем, что из истинности предполож-я при n=k истинность при n=k+1 4. индукционный вывод Т.к. предполож. истинно при n=1 а из истинности при n=k истинность при n=k+1истинно при n=2,3,4… истинно для n |
14. Декарт пр-ние n мн-в, n-арные отн-ния, классич операции над отношениями. Кортеж или n-ка – посл-ть эл-тов, т.е. мн-во, в котором каждый эл-т занимает определенное место. Обозначается кортеж как: (a1,a2,…,an), а a1,a2,…,an суть его эл-ты, которые называются компонентами кортежа, их число – длина кортежа. Декар пр-ние A1A2…An мн-в A1,A2,…,An представляет собой мн-во всех упоряд n-к эл-тов (a1,a2,…,an), где a1A1, a2A2, …, anAn. В этом случае а1 назыв 1ой корд-той и т.д. В частности, декартово пр-ние RRR, где R – мн-во действительных чисел, определяет трехмерное геометрич пр-во, где эл-ты a=(x,y,z) явл точками трехмер евклидового пр-ва. N-арным (или n-местным) отношением называется любое подмн-во Т декартова пр-ния n-й степени: T Mn. Точками отношения T являются посл-ти вида (a1,a2,…,an), где aiM. Для n-арных отношений операции вводятся аналогично бинарным отношениям.
Таким
образом, если T
и S
суть n-местные
отношения в мн-ве M,
то n-местными
отношениями в М
будут также следующие подмн-ва: TS,
TS,
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1. Понятие множества, подмножества, пустого множества. Диаграммы Венна. Мн-во – неопределенное понятие, которое характеризуют перечисление его свойств.
Подмн-во
А мн-ва В – мн-во, состоящее из элементов,
обладающих следующим св-вом:
Мн-во, которое не содержит эл-тов, называется пустым мн-вом и обозначается символом . Диаграммы Венна —инструмент, позволяющий изображать множества и иллюстрировать операции над ними. Множества в диаграммах Венна изображаются внутренними частями кругов, их пересечениями, объединениями и т.д. Прямоугольник изображает универсальное множество.
Рисунки
вида
|
15. Реляционные операции над отн-ми: операции выбора, проекции и соединения. В реляционных операциях рассматриваются только одноэлементные отношения. Пусть Т – отношение над множеством А со схемой отношений М={M1,M2,…Mn }. А) Выбор по атрибуту Мi со значением а осуществляется следующим образом: те стоки, в которых в i-ом столбце нет элемента а, вычёркивается. Свойства операции выбора:
Операция обобщённого выбора: σ mx(T) осуществляется выбором тех строк, у которых значение атрибута Мi линий в выбранном подмножестве х, при этом остальные строки зачёркиваются. Б) операция проекции хR(T) (где R – схема отношения) осуществляется выбором столбцов, принадлежащих х, при этом остальные столбцы вычёркиваются и при этом из одинаковых строк остаётся лишь одна. Таким образом формат отношения при операции проекции уменьшается, а не увеличивается. В) Операция соединения – бинарная операция, т.е. она применяется к 2 отношениям и в результате получаем новое отношение. Оно обозначается T►◄S. Пусть схема отношения Т равна R1, а схема отношения S равна R2, тогда схема отношения T►◄S есть R=R1UR2. Соед-ем отн-ний T и S будет мн-во таких картежей q, что для q существует два картежа qT и qS, что если вычеркнем из картежа q атрибуты, не входящие в Т, то получим картеж qT, а если вычеркнем из картежа q атрибуты. Не входящие в S, то получим картеж qS. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2. Оп-ции об-ния, перес-ния мн-в, опр-ние и св-ва ком-ти и ассоц-ти.
Объединением
2х мн-в А и В называется мн-во С, состоящее
из всех элементов, принадлежащих хотя
бы одному из мн-в А и В, т.е. АВ=
Пересечением
2х мн А и В наз-ся мн С, сост из всех
эл-тов, принадл-их как мн А, так и мн-ву
В, т.е. АВ=
Аналогично
определяется об-ние и перес-ние любого
(конеч или бесконеч) числа мн-в. Если
Ai
– произвол мн-ва, то их сумма (объединение)
А – есть совокупность элементов,
каждый из которых принадлежит хотя
бы одному из мн-в Ai.
Это обозначается
Пересечением
любого (конеч или бесконеч) числа мн-в
Ai
называется совокупность А элементов,
принадлежащих каждому из мн-в Ai.
Это обозначается
Оп-ции объед-ния и перес-ния ком-ны, т.е. для них выполняется переместит закон: АВ=ВА АВ=ВА Также эти операции ассоциативны, т.е. для них выполняется сочетательный закон: (АВ)С=А(ВС) (АВ)С=А(ВС) Эти св-ва операций следуют из их определения. Взаимная дистрибутивность операций пересечения и объединения. Операции пересечения и объединения взаимно дистрибутивны, т.е. для них выполняется распределительный закон: (АВ)С=(АС)(ВС) (1) (АВ)С=(АС)(ВС) (2) Док-ва этих теоретико-множественных равенств проводятся в обе стороны, т.е. для док-ва того, что А=В, показывают, что с одной стороны АВ, а с другой стороны АВ. Док-во (1). (АВ)С (АС)(ВС), x, x(АВ)С xA или хВ и хС (хА и хС) или (хВ и хС) хАС или х ВС х(АС)(ВС); (АВ)С (АС)(ВС) док-ся аналогично, все стрелки можно обернуть. Док-во (2). (АВ)С (АС)(ВС), x, x(АВ)С xA и хВ или хС (хА или хС) и (хВ или хС) хАС и х ВС х(АС)(ВС); (АВ)С (АС)(ВС) док-ся аналогично, все стрелки можно обернуть. |
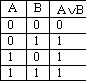
12.Логика высказ. Лог связки. Ф-лы логики высказ. Подформула, Ранг формулы. Логика высказываний — это формальная теория, основным объектом которой служит понятие логического высказывания. Несмотря на свою важность и широкую сферу применения, логика высказываний является простейшей логикой и имеет очень ограниченные средства для исследования суждений Высказыванием наз повеств предложение, про кот. можно сказать истинно оно или ложно. Определение. Формулами логики высказываний называются выражения вида (F)^(G), (F) ˅ (G), не(F), (F)-> (G), (F)<>(G) Подформулой формулы А называется любое подслово А, само являющееся формулой. Например, формула F=X&Y->X˅Z имеет шесть подформул: X,Y,Z,X&Y, X˅Z, X&Y->X˅Z. Ранг – это число высказывательных операций. Логические операции: Отрицанием высказывания А наз такое высказывание, к-рое истинно, когда А-ложно и ложно, когда А-истинно. А – «не А». Конъюнкцией высказываний А и В наз высказывание, к-рое истинно, когда А-истинно и В-истинно и ложно во всех ост случаях. A&B, AB, AB – «А и В». Дизъюнкцией высказываний А и В наз высказывание, к-рое ложно, когда А-ложно и В-ложно и истинно во всех ост случаях. АВ, А+В – «А или В». Импликацией высказываний А и В наз высказывание, к-рое ложно, когда А-истинно, а В-ложно и истинно во всех ост случаях. АВ, АВ – «из А следует В». Эквиваленцией высказываний А и В наз высказывание, к-рое истинно, когда А и В принимают одинаковое значение и ложно во всех ост случаях. АВ, АВ – «А эквивалент В». Штрих Шеффера, обычно обозначаемый |, эквивалентен операции И-НЕ и задаётся следующей таблицей истинности:равен нулю только при 11.
С
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3. Операция вычитания мн-в, отсутствие коммутативности и ассоциативности.
Разностью
2х мн-в А и В называется совокупность
тех эл-тов мн-ва А, кот. не содер-ся в
мн-ве В, т.е. С=А\В={x
| xA,
x
не
В }. В не может быть подмн-вом мн-ва А.
Операция вычитания некоммутативная
и неассоциативная, подобно операции
вычитания чисел в арифметике. Если
отсутствие коммутативности практически
очевидно:
|
13.Таблица истинности. Равносильность формул. Тавтологии. Две формулы алгебры логики A и B называются равносильными, если они принимают одинаковые логические значения при любом наборе значений входящих в формулы элементарных высказываний (переменных).
Обозначение. A≡B.
Пример . Ф-ла наз ТИ-высказыванием (или тавтологией) она принимает значение «1» набора выск-х переменных. Ф-ла наз ТЛ-высказыванием она принимает значение «0» набора выск-х переменных. Ф-ла наз выполнимой набор выск-х переменных, при к-ром она принимает значение «1». Ф-ла наз невыполнимой она принимает значение «0» набора выск-х переменных. Основные равносильности.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4. Симметрическая разность, определения и св-ва.
Симметрической
разностью
2х мн-в А и В называется сумма разностей
А\В и В\А
Док-во: АВ (АВ) \ (АВ), x, x(А\В)(В\А) xA\B или хВ\А (хА и хВ) или (хВ и хА) 1) хА и хАВ, 2) хВ и хАВ х(АВ)\(АВ); в обратную сторону аналогично. Операция является и коммутативной, и ассоциативной: АВ=ВА, (АВ)С=А(ВС). |
5. Операция дополнения мн-в, принцип двойственности.
Дополнением
к мн-ву А является мн-во
Принцип двойственности для 2х мн-в:
1)
2)
Док-во
(2):
Док-во (1) аналогично. Принцип двойств-ти состоит в том, что из люб рав-ва, состоящего из с-м подмн-в осн мн-ва С, может быть получено двойственное рав-во путем замены кажд рассматриваемого мн-ва его дополнением, объединений мн-в – их пересечениями, а пересечений – объединениями. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Принцип двойственности
|
14. Полные и не полные системы пропозициональных операций примеры с док-ом Теорема о приведенной форме ( с доказательством). 14 Полные и неполные системы пропозициональных операций. Примеры полных и неплоных систем(с док-вом) Теорема о приведенной форме Def Формула имеет приведенную форму она не содержит импликаций(->) и эквиваленций,а знак отрицания может стоять только над высшей переменной. Теорема о приведенной форме: Любая формула эквивалента некоторой приведенной форме. Док-во Из 16) (A->B)~(-A\/B)=>импликация может быть устранена Из 19) (A~B)~((-A\/B)/\(A\/-B))=>эквивваленция также может быть устранена Пользуясь законами де Моргана,постепенно снимаем отрицание с подформул,пока оно не будет стоять над высказывательной переменной. Система высказывательных переменных назыв. Полной если любая формула эквивалента некоторой формуле,в которую входят высказывательные операции(Базис). В этом случае говорят, что система высказ-х операция обретает базис Теорема системы операций < --, /\, \/> явл. Полным (образуют базис) Док-во < --, /\, \/>,т.к из 16,19 законов устраняются импликация и эквивалентность < --, \/> т.к (A/\B)~ --(-A\/-B) => устраняется /\ Утверждение системы < /\, \/> не явл. Полным Док-во Если формула А зависит от выск.переменных А(х1,х2,х3…хn) и все выск-е переменные системы имеют значение 1, то А(x1,x2…xn)=1 из ТИ /\ и \/ А в формуле,содержащей отрицание может получиться 0, то и все х1,х2,..хn имеют значение 1 Например, х1 -x2
=> Эта формула не может быть выражена без -- . х\/--x=1 Утверждение < -- > не явл.полной системой Док-во: т.кс помощью – могут быть выражены только формулы,содержащие выск.переменную Существуют операции,образующие полную систему. Одна из них штрих Шеффера,а другая стрелка Пирса
Ф-ла наз приведенной она не содержит импликации и эквиваленции, а отрицание может стоять только над высказ-й переменной. Теорема. ф-лы А эквивалентная ей приведенная ф-ла. Док-во: 1)избавляемся от всех и по 16 и 19 законам. Получили А А 2)докажем теорему индукцией по rank(A’) I база индукции: r(A’)=0 => A'=Xi – высказ переменная явл приведенной. II индукц предположение: предположим, что утвержд теоремы истинно A’ rank(A’)<=k III индукц шаг: док-м, что из истинности т-мы при rang(A’)<=k => истинность т-мы при при rang(A’)=k+1 Возможны случаи: A’=B, A’=B&C, A’=BvC, (rank(B)<=k и rank(С)<=k) по инд-му предположению B и C суть приведенной ф-лы (B&C), (BvC) – прив-е ф-лы. Док-м случай A’=B => rank(B)=k => к B применимо индукц предположение. B=C => C – высказ переменная B=Xi => A’=B=Xi =Xi – приведен. B=C&D, B=CvD => A=B= (C&D) = C v D rank(A)=k+1, rank(B)=k B=C&D =>rank(C)<=k-1, rank(D)<=k-1 => rang(C)=k, rank(D)=k => к C и D применимо инд-е предположение => C и D – м.б.приведенные => C v D - также приведенные.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
15.Элементарные конъюнкции и дизъюнкции. Теоремы о тождественной истинности элементарной дизъюнкции и тождественной лжи элементарной конъюнкции. Элементарной дизъюнкцией называется дизция высказывательных переменных или их отрицаний . Элементарной конъюнкцией называется конция высказывательных переменных или их отрицаний . Элементарная дизъюнкция является тождественно истинным высказыванием(принимает значении 0 при любом наборе высказывательных переменных)она наряду с некоторой высказывательной переменным содержит её отрицание <= очевидно . =>от противного ;предположим ,что существует элементарная дизъюнкция, у которой не существует высказывательных переменных, входящих в дизъюнкцию вместе со свои отрицанием. Придадим значение «0» тем выск. Переменным ,которая входит без отрицания и «1» тем выс. Переменным, которые входят с отрицанием получаем 0U0U0U0=>элементарная диз-ция не является ТИ-высказыванием. =>от противного ;предположим ,что существует элементарная конъюнкция, у которой не существует высказывательных переменных, входящих в конъюнкцию вместе со свои отрицанием. Придадим значение «0» тем выск. Переменным ,которая входит без отрицания и «1» тем выс. Переменным ,котороые входят с отрицанием получаем 0U0U0=>элементарная конция не является ТИ-высказыванием. Теорема1.Для того ,чтобы элементарная дизъюнкция была тождественно истинной, необходимо и достаточно ,чтобы в ней содержалась переменная и ее отрицание Для того, чтобы формула алгебры логики А была тождественно истинна, необходимо и достаточно, чтобы любая элементарная дизъюнкция, входящая в КНФ А, содержала переменную и её отрицание. Теорема2.Для того ,чтобы элементарная конъюнкция была тождественно ложной,необходимо и достаточно ,чтобы в ней содержалась переменная и ее отрицание Для того, чтобы формула алгебры логики А была тождественно ложна, необходимо и достаточно, чтобы любая элементарная конъюнкция, входящая в КНФ А, содержала переменную и её отрицание. 16Теоремы о КНФ и ДНФ. КНФ- конъюнкция элементарных дизъюнкций. ДНФ- дизъюнкция элементарных дизъюнкций. Теорема .Любая формула эквивалента некоторой КНФ(ДНФ). По теореме о приведенной форме любая формула эквивалентна приведенной=>считаем формулу приведенной . Доказательство методом математической индукции по рангу приведенной . Ранг – это число высказывательных переменных . I)База r(A)=0 A=xi-КНФ(ДНФ) II)предположим ,Что утверждение истинно при r(A)<k III)Инд. Шаг ,докажем , что если утв. Теорема истинной при r(A)<k=>r(a)=k; 1) А = (неВ1), след. В1=х1, т.к. А-приведенная, след. А=(не xi) – КНФ. 2) А = B1/\B2 – КНФ, т.к. B1, B2 – КНФ 3) A=B1\/B2 = (С1/\C2/\...Ce)\/(D1,D2,…Dm) = ((C1\/D1)/\(C1\/D2)/\...(C1\/Dm)/\(C2\/D1)…/\(Ce\/D1)/\(Ce\/D2)…(Ce\/Dm)-КНФ. К формулам В1 и В2 применимо индукционное предположение, значит считаем их КНФ.
17.Полные элементарные конъюнкции и дизъюнкции. Теорема об эквивалентности ПЭК некоторой СДНФ. Полная элементарная конъюнкция – это конъюнкция в которую входит каждая высказывательная переменная системы, либо её отрицание, при этом ровно один раз. Полная элементарная дизъюнкция – это дизъюнкция в которую входит каждая высказывательная переменная системы, либо её отрицание, при этом ровно один раз. Теорема. Всякая элементарная конъюнкция, не являющаяся ТИ высказыванием эквивалентная некоторой СДНФ. Д-во : Пусть X1,Х2,…,Хn=система высказывательных переменных Yi1˅Yi2˅…˅Yik Элементарная конъюнкция, в которую входят k высказывательных переменных или их отрицание ,где k<=n. Не ограничивая общности высказывания, считаем , что одинаковых индексов нет ,т.к. Yij˅YijYij, Yij˅¬Yij=1=>вся конъюнкция оказалась бы ТИ-высказыванием . I)сл. k=n=>Yi1˅…˅Yik-ПЭК→она представляет СДНФ II)сл. k<n=>ᴲ Ye не встречается в конъюнкции. Yi1˅Yi2˅…˅Yik~Yi1˅Yi2˅…˅Yik˅(Ye^¬Ye)~(Yi1˅Yi2˅Yik˅Ye)^(Yi1˅Yi2˅…˅Yik˅Ye). Пополн т.о. все всходящие конъюнкции пока в них не войдут все высказывательные переменные сисетмы, получим дизъюнкцию ПЭК, т.е. СДНФ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
6. Разбиение мн-ва, покрытие мн-ва, примеры в математике и информатике.
Представление
заданного мн-ва в виде объединения
системы мн-в, не имеющих попарно общих
точек, называется разбиением.
Таким образом, если есть мн-во А, такое
что
П
Любое
мн-во подмн-в мн-ва А, объединение
которых есть мн-во А, называется
покрытием мн-ва А. Сл-но, если есть
мн-во А, такое что
Пример. Мн-во натур чисел можно представить в виде об-ния мн-ва нечет чисел, мн-ва чисел, не дел на 3, и мн-ва чисел кратных 6. Очевидно, что эти подмн-ва пересекаются, на пример, число 7 принадлежит и мн-ву нечетных чисел, и мн-ву чисел, не делящихся на 3. |
17.Полные элементарные конъюнкции и дизъюнкции. Теорема об эквивалентности ПЭК некоторой СДНФ. Полная элементарная конъюнкция – это конъюнкция в которую входит каждая высказывательная переменная системы, либо её отрицание, при этом ровно один раз. Полная элементарная дизъюнкция – это дизъюнкция в которую входит каждая высказывательная переменная системы, либо её отрицание, при этом ровно один раз. Теорема. Всякая элементарная конъюнкция, не являющаяся ТИ высказыванием эквивалентная некоторой СДНФ. Д-во : Пусть X1,Х2,…,Хn=система высказывательных переменных Yi1˅Yi2˅…˅Yik Элементарная конъюнкция, в которую входят k высказывательных переменных или их отрицание ,где k<=n. Не ограничивая общности высказывания, считаем , что одинаковых индексов нет ,т.к. Yij˅YijYij, Yij˅¬Yij=1=>вся конъюнкция оказалась бы ТИ-высказыванием . I)сл. k=n=>Yi1˅…˅Yik-ПЭК→она представляет СДНФ II)сл. k<n=>ᴲ Ye не встречается в конъюнкции. Yi1˅Yi2˅…˅Yik~Yi1˅Yi2˅…˅Yik˅(Ye^¬Ye)~(Yi1˅Yi2˅Yik˅Ye)^(Yi1˅Yi2˅…˅Yik˅Ye). Пополн т.о. все всходящие конъюнкции пока в них не войдут все высказывательные переменные сисетмы, получим дизъюнкцию ПЭК, т.е. СДНФ 18. Теоремы о СКНФ и о СДНФ. Теорема о СКНФ. Любая формула ^B, не является ТИ-высказыванием, эквивалентным некоторой СКНФ. Док-во. По теореме о КНФ любая формула эквивалентная некоторой КНФ=>считаем, что данная формула А дана в КНФ. Зачеркиваем те элементарные дизъюнкции, которое являются ТИ-высказыванием, т.к. x^1~x. По теореме 1 остальные элементарные дизъюнкции эквивалентны некоторой СКНФ. Проведем все элементарные дизъюнкции к СКНФ и получим конъюнкцию ПЭД. Исключив повторяющиеся ПЭД получим СКНФ. Теорема о СДНФ. Любая формула ^B, не является ТИ-высказыванием, эквивалентным некоторой СДНФ. Док-во. По теореме о ДНФ любая формула эквивалентная некоторой ДНФ=>считаем, что данная формула А дана в ДНФ. Зачеркиваем те элементарные конъюнкции, которое являются ТИ-высказыванием, т.к. x^1~x. По теореме 1 остальные элементарные конъюнкции эквивалентны некоторой СДНФ. Проведем все элементарные дизъюнкции к СДНФ и получим конъюнкцию ПЭК. Исключив повторяющиеся ПЭК получим СДНФ.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
27-28. Определение слова, подслова, префикса, суффикса, собственного подслова, собственного префикса и суффикса, их свойства. равенства слов, операции приписывания, свойства операции приписывания. Множ-во символов- алфавит; элементы алфавита-буквы def СЛОВО - любая буква есть слово;
- если
А – слово и В – слово, то АВ – также
слово
- пустое слово /\ (слово, не содержащее букв) есть слово. Слово В есть подслово слова D, если А С D≡ABC Слово С есть собственное подслово слова А, если сущ-ют такие слова В и D, что А имеет вид ВСD и хотя бы одно В или D не пусто. Сл С называется префиксом сл В С≡АВ Св-ва префикса:
Слово наз собственным префиксом слова С А-префикс С и А≠С Св-ва собственного префикса: Если А и В суть собств префиксы сл С, то А есть собств преф В или В есть собств преф А. Слово А тогда и только тогда есть префикс ВС, когда имеет место одно из двух: А – собственный префикс слова В или А имеет вид ВD, где D – префикс С. Суффиксом(концом) сл С наз сл В А С≡АВ (Сл С-конец сл А, если сл В |А≡ВС) Св-ва суффикса: 1) слово есть суффикс самого себя. (/\ | /\ есть приписыв-е пустого слова и самого себя.) 2) Пустое слово есть суффикс любого слова. (док-во в 1ом св-ве) 3) Если А–суффикс В, а В–суф С, то А–суф С (св-во транзитивности суф). Док-во: если А–суф В, то сл D | B≡DА, т.к. В–суф С, то сл Е |С≡ЕВ, тогда С≡ЕDА и А–суфС. А–собственный суф В, если А – суффикс В и А≠В Св-ва собственного суффикса: 1) Если А и В суть собственные суф сл С, то А есть собств. суф В или В есть собств. суф А. 2) Сл А есть суф ВС когда имеет место 1 из двух: А – собств. суф сл С или А имеет вид DС, где D – суф С. def 2 слова А и В наз. равными в лексикографическом смысле |A|=|B| и i i-ая буква слова А совпадает с i-ой буквой слова B. (Если два слова А и В построены из одинаковых букв, располож. в одинаковом порядке, слова А и В графически равны) Слова строятся с пом. операции приписывания (конкатенации), т.е. к слову А приписывается справа слово В. Св-ва операции приписывания:
|
19. Понятие графа, примеры. Задачи, послужившие основой теории графов (задача о кенигсбергских мостах, задача о четырёх красках). Графом G наз-ся совокупность 2-х мн-в: мн-ва вершин и мн-ва пар вершин, наз-ых ребрами вершин. G =(V, А), где V – мн-во вершин, А – конеч. мн-во ребер. Vj – начало ребра. Vk – его конец. Если пара вершин соедин. 2 и более ребрами, то ребра – кратные. Если ребро нач-ся и закан-ся в одной и той же вершине, то ребро наз-ся петлей. Вершины графа, соедин. 1 ребром, наз-ся смежными. Ребро и любая из 2х его вершин наз-ся инцидентными. Степенью вершины наз-ся число ребер, инцидентных ей. Если вершина имеет степень 1, то она наз-ся висячей, если степень 0 – изолированной. Граф, допус-й кратные ребра– мультиграф. Допускающий кр. ребра и петли– псевдограф. Граф, в котором нет кратных ребер и петель, называется простым. Задача о кенигсбергских мостах (1736 Л. Эйлер)
Ж Зад.о 3 дома и 3кол.. Имеется 3 дома и 3 колодца, располож. на пл-ти. Провести от каждого дома к каждому колодцу тропинку,так, чтобы они не пересекались. Задача была решена (показано, что решения не существует) К Куратовским в 1930. Задача о 4 красках. Разбиение плоскости на непересек-ся области наз-ся картой. Области карты называются соседнимиони имеют общую границу. Задача состоит в раскраш. карты так, чтобы никакие 2 области не были закрашены одним цветом, а теорема состояла в том, что любая карта, не имеющая анклавов (территория, окруж.со всех сторон террит. другого гос-ва) может быть раскрашена 4 красками. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
29 Определение кода. Пусть П={a1,a2,…,am}-алфавит; мн-во слов {b1,b2,…,bn}в этом алфавите наз кодом -й перестанови любого подмнож-ва множ-ва символов {1,2,..,n} не bi1bi2…bik≡bj1bj2…bjl где {i1, i2,..,ik},{j1, j2,..jl}<{1,2,..,n} (Мн-во слов {b1,b2,…,bn} в алфавите П={a1,a2,…,am} называется кодом, если не сущ-ет такой перестановки {i1,i2,…,in} символов {1,2,…,n}, что b1b2…bn=bi1bi2…bin.) B={ab; abb} – код. B={a; b; ab}, (где a=b1, b=b2, ab=b3) – не код, т.к. b1b2b3b3b1b2. Теорема для кодировки -го конечного алфавита код, использующий две буквы. Док-во: пусть используемым алфавитом явл {0;1} i a1 = 0…01, где 0..0 – i раз. Заданное отображение является биекцией
|
20. Ориентированный граф, двудольный граф, примеры. Пути и циклы в графах. Критерий простого цикла.
Если пары (Хi,Хj) упорядоч. (не допускается перестановка вершин), то граф наз. ориентированным и пара вершин наз. дугой. Vj – начало ребра. Vk – его конец. Путем наз послед-ть ребер, в кот 2 координата предыдущ. ребра совпад. с 1 коорд. последующ. ребра и ни одно ребро не встречается дважды. Если путь не проходит дважды через 1 и ту же вершину, то он наз простым. Длиной пути наз кол-во ребер в нем. Циклом наз путь, кот. начин. и заканч-ся в 1 и той же верш. Если цикл не проходит дважды через 1 и ту же верш., то он наз простым. Длиной цикла наз кол-во ребер в нем. Т1 (Критерий простого цикла) Чтобы граф G представлял собой простой цикл каждая его вершина имела степень 2. =>Для его вершины Xi в нее 1 раз вошли, и 1 раз вышли => deg(Xi)=2 <=Докажем индукц. по кол-ву вершин.
1 2 шаг. Предп-им, что теор верна при кол-ве вершин = k 3 шаг. Док-м что из истин-ти утверж. при n=k след-т истин-ть n=k+1: Для люб. Xi –удалим Xi. Имеем, для люб. j≠i±1 deg(Xj)=2, а для Xi-1 и Xi+1 степень стала равна 1. Соедин. Xi-1 и Xi+1 новым ребром, тогда deg(X i±1)=2 Получ. граф G1, удовлетв. инд. предпол., след-о он представл. собой простой цикл ({X1…Xi-1,Xi+1… Xк+1},{(X1,Х2);(Х2,Х3);…(Xi-1, Xi+1)…(Xк+1,Х1)})- G1 Восстанов. Xi и после восстановл. имеем: ({X1…Xi-1,Xi,Xi+1… Xк+1};{(X1,Х2);(Х2,Х3);…(Xi-1, Xi),(Xi, Xi+1)… … (Xк+1,Х1)}) – простой цикл. 4 шаг. Предл. истин. при n=3, а из истин-ти предл. при n=k след-т истин-ть n=k+1, значит истинно при n=4,5…
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
7. Декартово пр-ние мн-в и его св-ва. Геометр интерпретация декарт пр-ний.
Декартовым
или прямым пр-нием мн-в А и В называют
мн-во АВ
всех упорядоченных пар эл-тов (a,b),
где aA,
bB,
т.е. АВ=С= Если одно из мн-в А или В пусто, то произв-нием АВ будет пустое мн-во. Известным примером явл-ся мн-во декартовых координат в прямоугольной сис-ме корд-т. Св-ва декартова пр-ния:
Для док-ва этих фактов достаточно привести примеры, когда коммутативность и ассоциативность не выполняются: Пример 1. Пусть A={1}, В={2,3}, тогда АВ={(1,2),(1,3)}, BA={(2,1),(3,1)}. Обратим внимание, что в случае, когда А=В, переместительный закон имеет место.
П Декартовым произведением явл плоскость. Например, А=[0,1] и В=[1,2), тогда АВ: Если А=В, то АВ =А2. Если одно из множеств является , то АВ= |
21. Компоненты связности, мосты. Критерий моста. Граф G наз связным, если для любых 2-х его вершин сущ путь, связ-й их, иначе граф наз несвязным. несвязн граф распад-ся на связные подграфы,кажд из кот явл компонентой связности. Компонента связности – максимально связный подграф. Подграфом G1=(V1, А1) графа G=(V, А) наз часть графа, кот сама явл графом. G=(V, А). Пусть V1 V и А1 А ; G1=(V1,А1). G1 явл подграфомдля (Xi, Xj)А1 верш, инцид ему и V1. Несвязный граф облад. таким св-вом, что люб. верш. не связана ни с одной верш. другой компоненты никаким путем. Мостом наз такое ребро, при удалении кот-го число комп. связности увел-ся. Т(критерий моста): Ребро графа G явл мостом оно не ни 1 из циклов. Док-во => от противного. Предпол. что сущ цикл, кот ребро (Хi,Хj) явл. мостом. При удал. (Хi,Хj) число комп. связн. увелич. (по опр. моста), и для Хk, Хn из разных комп-т нет пути, их соединяющего, а до удал. (Хi,Хj) путь был, содержал (Хi,Хj) и имел путь: {(Xк, Xк+1)…(Xi,Xj)… (Xn-1, Xn)}). заменив (Хi,Хj) на обходной путь (т.к. ребро циклу) получ новый путь из Хk в Хn. Получ. противоречие. Док-во <= Предполож, что такое ребро (Хi,Хj), кот не явл-ся мостом и не ни одному из циклов. Тогда удалим (Хi,Хj). Т.к. (Хi,Хj) – не мост, то число компонент связности не изменилось, путь из Хi в Хj {Xi,Xi+1,…Xj-1,Xj}. Восстановив ребро (Хi,Хj) получ. цикл. Противоречие. Ч.т.д.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
8. Понятие бинарного отношения, способы задания отношений интерпритация графа, как бин отн-гий, задание графа с помощью матрицы Отношение – бинарное отношение – любое подмножество вида АА. Пусть A=R, в этом случае отношение “<” означает множество пар декартовой плоскости, расположенное левее биссектрисы 1 и 3 координатных углов. пример А{123456}, R{(ai;aj)(ai:.aj)}
8. св-ва бинарных отношений: рефлексивность, симметричность, интисимметричность, транзитивность. Свойства:
Тогда в матрице отношения R на главной диагонали стоят только единицы: i cii=1
На главной диагонали матрицы есть хотя бы один ноль.
Тогда на главной диагонали матрицы стоят только нули: i cii=0.
Т
В матрице такого отношения должно выполняться след условие: если cij=1 и cjk=1 i, j, k Говорят, что в М задано бинарное отношение Т, если ММ есть декартово произведение и в ММ выделено произвольное подмн-во Т. Таким образом, произвольное подмн-во ТММ есть бинарное отношение. Мы будем говорить, что эл-т a находится в отношении Т к эл-ту b в том и только в том случае, когда пара (а,b) принадлежит мн-ву Т. Для этого возможны два равносильных способа обозначения: аТb или (а,b)Т. |
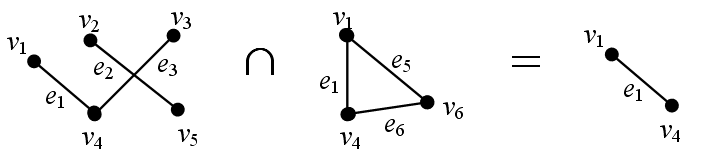
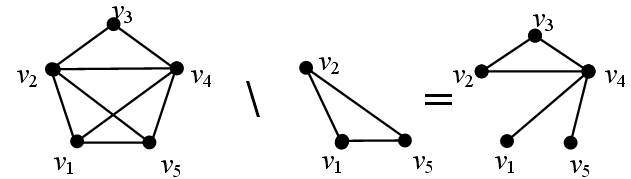
21. Понятие подграфа. Реберно-порожденный подграф. Основные операции над графами.
П Граф G1=(V1, А1) наз реберно-порожд. подграфом графа G, когда V1 содержит все вершины графа G, инцидентные ребрам из А1. Операции над графами:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
9. Отношение эквивалентности, определения, примеры. Теоремы о связи разбиения множества и отношением эквивалентности на нем Бинарное отношение ТММ называется отношением эквивалентности, заданном на мн-ве М, тогда и только тогда, когда оно удовлетворяет следующим трем усл-виям: a, aM (a,a)T, т.е. отношение Т удовлетворяет усл-вию рефлексивности ab, aM, bM если (a,b)T, то (b,a)T, т.е. отношение Т удовлетворяет усл-вию симметричности abc, aM, bM, cM если (a,b)T и (b,c)T, то (a,c)T, т.е. отношение Т удовлетворяет усл-вию транзитивности Таким образом, эквивалентность есть бинарное отношение, удовлетворяющее усл-виям рефлексивности, симметричности и транзитивности. Отношение равенства чисел есть отношение эквивалентности, т.к. является рефлексивным, симметричным и транзитивным. А бинарное отношение «<» для чисел не явл отношением эквивалентности, т.к. оно не удовлетворяет условию симетричности.
Разбиение
множества.
Пусть А — произвольное множество.
Семейство Для любого отношения эквивалентности на множестве А множество классов эквивалентности образует разбиение множества А. Обратно, любое разбиение множества А задает на нем отношение эквивалентности, для которого классы эквивалентности совпадают с элементами разбиения. отношение эквивалентности P на множестве A определяет некоторое разбиение этого множества. Убедимся вначале, что любые два класса эквивалентности по отношению P либо не пересекаются, либо совпадают.
Пусть
два класса эквивалентности [X]p
и [Y]p имеют
общий элемент
Обратно,
если
Итак,
любые два не совпадающих класса
эквивалентности не пересекаются. Так
как для любого
Теперь
пусть
Очевидно,
что введенное отношение рефлексивно
и симметрично. Если для любых
31Отношения нестрогого порядка, определения, примеры. Говорят, что отношение нестрогого порядка задано на мн-ве М, если Т есть бинарное отношение, подчиненное следующим трем усл-виям:
Таким образом, отношение нестрогого порядка есть бинарное отношение, удовлетворяющее усл-виям рефлексивности, антисимметричности и транзитивности. Пример 1. Отношение «» для чисел есть отношение нестрогого порядка. Действительно, для любых действительных чисел a,b,c выполняются все три условия: аа; если аb и ba, то a=b; если ab и bc, то ac. Пример 2. Отношение «быть подмн-вом» также явл отношением нестрогого порядка, т.к. любое мн-во явл подмн-вом самого себя, а также, если АВ и ВА, то А=В, и, наконец, если АВ и ВС, то АС. Отношения строгого порядка, определения, примеры. Говорят, что на мн-ве М задано отношение строгого порядка Т, если есть бинарное отношение, подчиненное следующим трем усл-виям:
Таким образом, отношение строгого порядка есть бинарное отношение, удовлетворяющее усл-виям антирефлексивности, несимметричности и транзитивности. Пример 1. Отн-е «<» для чисел есть отн-е строг порядка. Так, про любое действит число a нельзя сказать, что a<a, для любых 2х действит чисел a,b либо a<b, либо b<a, и значит, они не могут иметь место одновременно. А для любых 3х чисел: если a<b и b<c, то a<c. Пример 2. Отн-е между людьми «один старше др» также явл отн-ем строгого порядка. |
22. Числовые характеристики графа: цикломатическое число, хроматическое число. Раскраска графов. Цикломатическим числом ν(G) графа G наз. наименьшее число ребер, удаление которых приводит к графу без циклов; ν(G) =m-n+k. где т - число ребер, n - число вершин, k - число компонент связности графа G. Хроматическим числом χ(G) наз. наименьшее количество цветов, которыми можно раскрасить вершины графа G так, чтобы любые смежные вершины были окрашены разными цветами. Правила раскраски графов:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
10. Упорядоченные мн-ва, определения, примеры. Два эл-та aM и bM являются сравнимыми в данном порядке TMM, если про них можно сказать, что (a,b)T или (b,a)T, или a=b. Мн-во М с введенным порядком Т является упорядоченным (линейно упорядоченным), если любые два эл-та этого мн-ва являются сравнимыми. Про мн-во М, на котором просто введен некоторый порядок Т, т.е. в котором существуют сравнимые эл-ты, говорят, что оно частично упорядоченно. Св-вом упорядоченности обладает мн-во всех точек на действительной числовой прямой R, т.к. любые два действительных числа можно сравнить между собой. Для отношения «быть собственным подмн-вом» это св-во не имеет места, т.к. по отношению включения можно сравнить далеко не все подмн-ва. Например, числовой интервал (-2,5) нельзя сравнить с отр-ком [0,7] по отношению включения. Таким образом, это мн-во является частично упорядоченным. Среди линейно упорядоченных мн-в выделяют вполне упорядоченные мн-ва. Для его определения введем определение усл-вия минимальности. Говорят, что мн-во М удовлетворяет усл-вию миним-ти для некот отн-ния порядка Т, если в люб его непуст подмн-ве XM существует такой эл-т a, что x xX, имеет место: аТх. Итак, мн-во назыв вполне упоряд-ым, если оно явл лин упоряд-ым и удовлетворяет усл-вию миним-ти. Например, мн-во натур чисел явл вполне упоряд-ым, а мн-во действит чисел не явл вполне упорядоченным, т.к. для интервалов не сущ-ет минимального эл-та. Обратим внимание на то, что одно и то же мн-во может быть линейно упорядоченным относительно одного порядка и лишь частично упорядоченным относительно другого. Например, мн-во людей с введенным отн-ем старшинства явл лин упоряд-ным (роль рав-ва играет отн-ние «быть ровесниками»), а это же мн-во с отн-нием «быть предком» не явл лин упоряд-ным, т.к. про любых 2х людей нельзя сказать, что один явл-ся предком другого. |
34 Операции над бинарными отношениями Так как отношения на Х задаются подмножествами rНXґY, для них определимы те же операции, что и над множествами:
Пример 13. Если r - «быть моложе», то r -1 – «быть старше». 6. Составное отношение (композиция) r1 · r2. Пусть заданы множества М1, М2 и М3 и отношения R1 Н М1 ґ М2 и R2 Н М2 ґ М3. Составное отношение действует из М1 в М2 посредством R1, а затем из М2 в М3 посредством R2, то есть (a, b) О R1·R2, если существует такое с О М2, что (а, с) О R1 и (a, c) О R2. 7. Транзитивное замыкание r°. Транзитивное замыкание состоит из таких и только таких пар элементов а и b из М, то есть (a, b)Оr°, для которых в М существует цепочка из (k+2) элементов М, kі 0, что а, с1, с2, …ck, b, между соседними элементами которой выполняется r. Другими словами а r с1, с1 r с2, …, сk r b. Пример 14. Для отношения «быть сыном» транзитивным замыканием является отношение «быть прямым потомком по мужской линии».
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
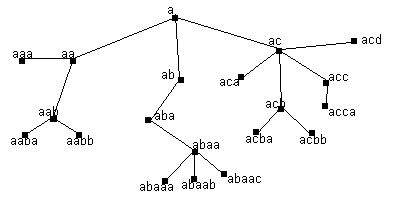
11. Деревья, лексикографический порядок, определения, примеры. Имеем некот алфавит. Заметим, что его мощность должна быть не меньше, чем макс число ветвлений в некот вершине дерева. Не ограничивая области, возьмем латин алфавит. Дерево в мате-ке строится сверху вниз. Пусть корень (начальная вершина) дерева назыв a. Тогда в 1ом ярусе самая лев вер-на есть аа, след – ab, затем – ac и т.д., во 2ом ярусе вер-ны, выход из вер-ны aa, имеют названия aaa, aab, aac и т.д., вер-ны, выход из вер-ны ab, имеют названия aba, аbb, аbc и т.д. Таким образом, вер-на, находящаяся в n-м ярусе, имеет названия длины n. Если из вер-ны не выходит ни одной ветви, то она называется концевой. Пример. В дереве естественным образом устанавливается отн-ние предшествования: одна вер-на предшествует др, если ее имя явл префиксом имени 2ой вер-ны. Так, вершина aa предшествует вер-не aabab. В этом порядке сравнимые вер-ны на 1ой ветви: та, которая находится выше, предшеств той, кот находится ниже. Такой порядок графич иллюстрирует соотн-ние между людьми «быть предком»; вер-ны, располож выше, изображают предка, а вер-ны, располож ниже, - потомков. Если рассматривать дерево на рис как генеал-кое, то аа есть прадед aabab. Разумеется, в этом порядке вер-ны дерева не представляют собой упоряд мн-ва, а лишь частич упоряд мн-во, т.к. вер-ны aaa и ababb не сравнимы.
В дереве на рис вер-на ab предш-ет вер-не ababb, а вер-на ababaa предш-ет вер-не ababab. В этом порядке число вер-н по-прежнему не явл упоряд-ым мн-вом; к примеру, вер-ны aabb и abab не явл сравнимыми, но теперь можно сравнивать вер-ны, выходящие из одной и той же вер-ны. В отн-ях между людьми это можно интерпретировать как отношение «быть или предком, или старшим братом». Иногда такой порядок называют «деревянным». Если для некот целей нужно, чтобы все вер-ны дерева были упорядоченными, то порядок можно определить следующим образом. Одна вершина предшествует другой в 2х случаях:
Этот порядок называется лексикографическим, алфавитным или словарным. |
23. Задачи о кратчайших путях: путь с наим. числом дуг, (путь кратчайшей длины). Путь наз кратчайшим, если он содержит наименьшее число дуг из всех возможных. Алгоритм построения наименьшего пути от верш а к верш b.
{x | y, y V(m)} где х и у смежны.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
12. Св-ва отображения, ф-ции графики. Ф-ции как част случай бинар отношений. Функцией называется функциональное соответствие. Если функция устанавливает соответствие между множествами А и В, то говорят, что функция имеет тип АВ (обозначается АВ). Каждому элементу а из области определения функция ставит в соответствие элемент b из области значений. Это обозначается (а)=b. Элемент а – аргумент функции, элемент b – значение функции на а. Отображением. А в называется всюду определённая функция. __ АВ. Отображением А на В называется всюду определённое и при этом сюръективное функциональное соответствие АВ. Отображением типа АА часто называют преобразованием множества А. Функция типа АА, являющаяся отображением А на А, называется перестановкой на А. Функции и g равны, если:
Функция типа А1А2…Аn назывется n-местной. В этом случае принято считать, что функция имеет n аргументов: (а1……аn)=b, где а1А1,……..,аnAn, bB. Если соответствие, обратное к функции АВ, является функциональным, то оно называется функцией, обратной к (обозначается -1). Для функции АВ обратная функция существует тогда и только тогда, когда является взаимно однозначным соответствием между своими областями определения и значений. Способы задания функции:
Если элемент а принадлежит множеству М, то соответствующий ему элемент d=(a) называется его образом. Каждый элемент а может иметь единственный образ, при этом для b может существовать не один элемент из М, образом котрого он является. Совокупност всех тех эл-тов а из М, образом которых является данный элемент b из N, называется прообразом или полным прообразом элемента b и обозначается -1(b). |
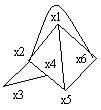
24. Теорема об эйлеровом цикле. Эйлеров цикл – сод-т все ребра графа и ни по одному нельзя пройти 2-ды. Теоp.Эйлеров цикл в связном графе когда все вершины имеют четную степень. Док-во. Необход-ть условия очевидна, так как при каждом прохожд цикла через к-либо вершину использ. 2 ребра - по 1 из них маршрут входит в верш, по др вых-т из нее (это относ. и к старт верш - в ней ведь маршрут должен закон-ся). Достаточность.
Пусть
G - связн граф, в кот-м > 1 верш и степени
всех вершин четны. Значит, степень
каждой вершины >= 2, поэтому по теореме
(критер прост цикла) в графе G имеется
цикл Z1. Если удалить все ребра этого
цикла из графа G, то пол-ся граф G1, в
кот-м степени вершин также четны. Если
в G1 нет ни одного ребра, то Z1- эйлеров
цикл. В прот случае, применяя ту же
теорему к графу, получ из G1 удалением
всех изолир-х верш, заключаем, что в
G1 имеется цикл Z2. Удалив из G1 все ребра
цикла Z2, получим граф G2. Продолжая
действовать т. о., пока не придем к
пустому графу, получим в итоге систему
циклов Z1….Zk, причем каждое ребро графа
в точности одному из них. Покажем
теперь, что из этих циклов можно
составить один цикл. Действительно,
из того, что исходный граф связен,
следует, что хотя бы один из циклов
Z1…Zk-1 имеет общую вершину с Zk. Допустим,
для определенности, что таков цикл
Zk-1. Пусть
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
13. Свойства функций: инъективность, сюрьективность, биективность. 1.Функция f называется инъективной (или, коротко, инъекция), если разным элементам множества X сопоставлены разные элементы множества Y. Более формально, функция f инъективна, если для любых двух элементов X1, X2 X таких, что f(x1) = f(x2), непременно выполняется x1 = x2. Другими словами, сюръекция — это когда «у каждого образа есть прообраз», а инъекция — это когда «разные — в разные». То есть, при инъекции не бывает так, чтобы два или больше разных элементов X отображались в один и тот же элемент Y. А при сюръекции не бывает так, чтобы какой-то элемент Y не имел прообраза. 2.Функция f называется сюръективной (или, коротко, сюръекция), если каждому элементу множества прибытия может быть сопоставлен хотя бы один элемент области определения. Другими словами, функция f сюръективна, если образ множества X при отображении совпадает с множеством Y: f[X] = Y. Такое отображение называется ещё отображением на. Если условие сюръективности нарушается, то такое отображение называют отображением в. 3.Если функция является и сюръективной, и инъективной, то такую функцию называют биективной или взаимно однозначной.
|
24 Алгоритм построения эйлерова цикла. Цикл называется эйлеровым, если ему принадлежат все ребра (и ни по одному ребру нельзя пройти дважды) выбрать произвол вел-ну а выбрать произвольно некоторое ребро, инцидентное а, и присвоить ему №1 каждое пройденное ребро вычеркивать и присваивать ему номер, на единицу больший номера предыдущего ребра находясь в некоторой вер-не х, не выбирать ребра, инцидентного а, если есть возможность другого выбора находясь в вер-не х, не выбирать мостов После того, как все ребра занумерованы ={1,2,…,n} – есть путь, образующий эйлеров цикл. |





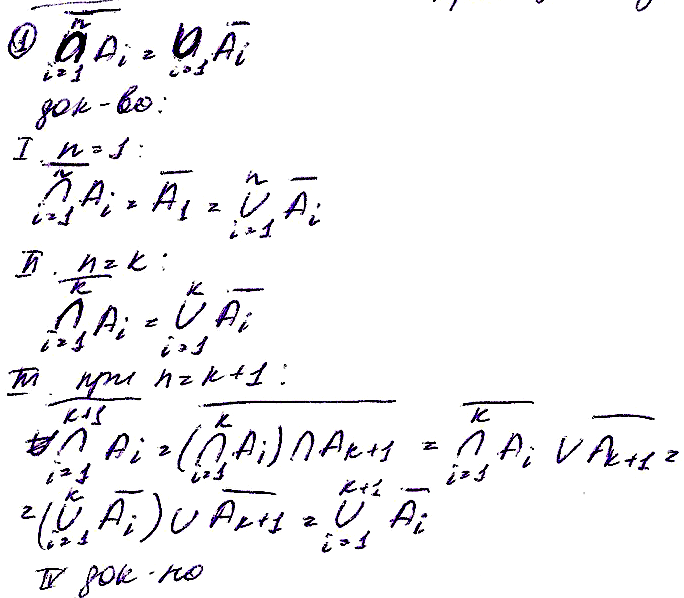
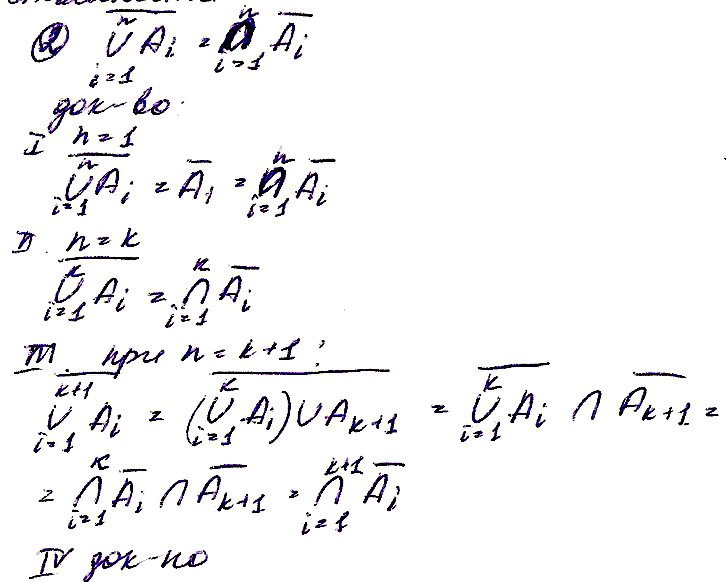
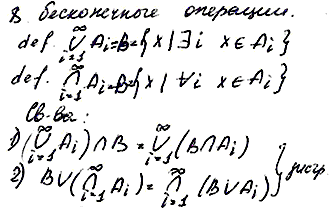

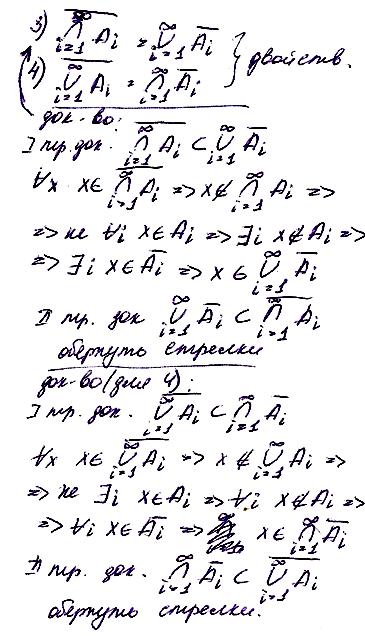

 ителям
Кен. (Калининград) нрав-сь гулять по
дорогам, кот-е включ. семь мостов,
соед-х. 2 острова и берега реки Преголя.
Люди интерес-сь, могут ли они, начав
путь с одного участка суши, обойти все
мосты, посетив каждый лишь 1раз, и
вернуться в точку начала пути, не
переплывая реку. Эйлер построил граф:
суша-вершины, а дорожки–ребра.Опираясь
на раннее сформулир. и доказаную теор,
Эйлер показал, что такого маршрута
нельзя построить. Классич. задачи: о
3
домах и 3 колодцах;
задача о 4 красках.
ителям
Кен. (Калининград) нрав-сь гулять по
дорогам, кот-е включ. семь мостов,
соед-х. 2 острова и берега реки Преголя.
Люди интерес-сь, могут ли они, начав
путь с одного участка суши, обойти все
мосты, посетив каждый лишь 1раз, и
вернуться в точку начала пути, не
переплывая реку. Эйлер построил граф:
суша-вершины, а дорожки–ребра.Опираясь
на раннее сформулир. и доказаную теор,
Эйлер показал, что такого маршрута
нельзя построить. Классич. задачи: о
3
домах и 3 колодцах;
задача о 4 красках.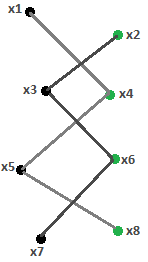
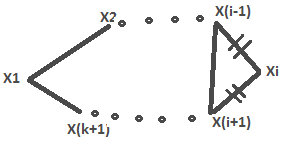 шаг. База инд. 3. При n=3 – верно (рисуем
треугольник)
шаг. База инд. 3. При n=3 – верно (рисуем
треугольник) огда
в матрице отношения i,j:
cij=сji=1.
Значит, матрица симметрична относительно
главной диагонали.
огда
в матрице отношения i,j:
cij=сji=1.
Значит, матрица симметрична относительно
главной диагонали.



 сли
все буквы, кроме последней, в них
совпадают, а последняя буква в 1ом
слове расположена в алфавите раньше,
чем последняя буква во 2ом слове.
сли
все буквы, кроме последней, в них
совпадают, а последняя буква в 1ом
слове расположена в алфавите раньше,
чем последняя буква во 2ом слове.