Лабораторная работа №1

Тема. Получение случайных чисел.

Цель работы. Научиться получать конечный набор значений случайной величины для разных законов распределения.

Теоретический материал. Компьютерное моделирование процессов функционирования стохастической системы, позволяющее получать статистические данные об этих процессах называют статистическим моделированием. Реализация статистического моделирования требует случайного задания исходных данных с известными законами распределения. Поэтому значения выходных переменных (характеристик исследуемых процессов) получаются как вероятностные оценки.

В соответствии с положениями математической статистики описание результатов наблюдений случайных величин использует понятие вероятности.

Фундаментальными понятиями статистической теории являются понятия генеральной совокупности и выборки. Генеральная совокупность – совокупность всех возможных результатов наблюдений над случайной величиной. Выборка – это конечный набор x₁, x₂, …, x_n значений случайной величины, полученный в результате наблюдений. Число элементов n выборки называется ее объемом или размером.

Интуитивно понятно, что чем больше объем выборки, тем более точно она должна отражать статистические свойства случайной величины.

Основными характеристиками распределения случайной величины, являются математическое ожидание и дисперсия.

Случайной называется величина, которая в результате опыта может принимать то или иное значение (какое именно, заранее неизвестно). Вероятностные свойства случайных величин описываются законом распреде­ления, т.е. соотношением, устанавливающим связь между возможными значе­ниями случайной величины и соответствующими им вероятностями. Закон рас­пределения может иметь различные формы. Различают дискретные и непрерывные случайные величины.

Дискретные случайные величины

Дискретной случайной величиной называют величину, принимающую только конечное или счетное множество значений. Для описания дискретной случайной величины X, принимающей конечное множество значений, часто применяется соотношения вида

xi	x1	x2	…	xn-1	xn
P(X=xi)	p1	p2		pn-1	pn

Здесь x_i — возможные значения случайной величины X, p_i = Р(Х = x_i) — ве­роятность события, что случайная величина X примет значение x_i (1 < i < n). Отметим, что

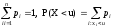
В последнем выражении суммирование ведется по всем таким номерам i, для которых х_г < и. Совокупность вероятностей p_i = Р(Х = x_i) часто называют функцией веро­ятностей, а вероятность Р(Х < и) обозначают как F(u) и называют функцией распределения случайной величины X.

Непрерывные случайные величины

Непрерывной случайной величиной называется случайная величина, возмож­ные значения которой непрерывно заполняют какой-либо интервал (в том числе, бесконечный). Для непрерывной случайной величины X в качестве закона распределения выступает функция распределения F(u), численно равная вероят­ности того, что случайная величина X окажется меньше заданного числа и, т.е. F(u) = Р(Х < и). Функция F(u) — непрерывная функция, неубывающая и при­нимающая значения в интервале от 0 до 1.

Отметим, что распределение непрерывной случайной величины невозможно задать с помощью вероятностей отдельных значений подобно распределениям дискретных случайных величин, поскольку Р(Х = x) = 0 для любого значения х. Но если функция F(u) дифференцируемая, то можно определить вероятность по­падания случайной величины X в какой-либо малый интервал длиной dx, при­мыкающий к точке х, и при этом Р(х <= X <= х + dx) = f(x)dx, где f(x) — произ­водная функции F(u) в точке х. Функция f(x) называется плотностью вероятности случайной величины X. Она может принимать только неотрица­тельные значения. Из определения плотности вероятности следует, что

U +∞ b

F(u) = ∫ f(x)dx, ∫ f(x)dx = 1, P(a < X < b) = ∫f(x)dx = F(b)- F(a).

-∞ -∞ a

Числовые характеристики случайных величин

Закон распределения полностью характеризует случайную величину. Чтобы оп­ределить закон распределения случайной величины, достаточно задать ее плот­ность вероятности или функцию распределения. Однако, для решения многих практических задач достаточно знать лишь некоторые числа, характеризующие распределение, так называемые числовые характеристики случайной величины. Из числовых характеристик наиболее часто используются моменты случайной величины. Первый момент называется математическим ожиданием (или средним случайной величины) и вычисляется по одной из следующих формул (первая форму­ла применяется для дискретных случайных величин, а вторая — для непрерывных):

MX=∑x_ip_i MX=∫xf(x)dx

Величина MX характеризует среднее положение значений случайной вели­чины X.

Второй центральный момент характеризует разброс значений случайной величины вокруг зна­чения MX и называется дисперсией. Дисперсию DX часто обозначение σ² или σ_х².

Равномерное непрерывное распределение. Непрерывная случайная величина ξ имеет равномерное распределение в интервале (a,b), если её функция плотности f(x) и распределения F(x) имеют вид:

или графически

В этом случае числовые характеристики случайной величины ξ, принимающей значения x – математическое ожидание, дисперсия и среднее квадратичное отклонение соответственно будут:

Если границы интервала a=0, b=1 то функции плотности и распределения имеют вид:

а математическое ожидание M|ζ| = 1/2 и дисперсия D|ζ| = 1/12. Получить это распределение на цифровой ЭВМ невозможно, так как машина оперирует с n-разрядными числами. По­этому на ЭВМ вместо непре­рывной совокупности равно­мерных случайных чисел ин­тервала (0, 1) используют дискретную последователь­ность 2n случайных чисел то­го же интервала. Закон рас­пределения такой дискрет­ной последовательности на­зывают квазиравномерным распределением.

Математическое ожидание и дисперсия квазиравномерной случайной величины имеют вид

Дисперсия отличается от дисперсии равномерно распределенной случайной величины только множителем (2ⁿ+1)/(2ⁿ-1.

Треугольное распределение. Случайная величина X имеет треугольное распределение на интервале [а, b], если ее плотность вероятности вычисляется по формуле

Для этой случайной величины МХ = (4(а³+b³)-(а+b)³)/ 6(b-a)², DX = (b-a)³/24. Если X_t и Х₂ — независимые случайные величины, равномерно распределенные на интервале [a/2, b/2], то случайная величина X = X₁ + Х₂ имеет треугольное распределение на интервале [а,b], представленное на рис. 1.1.

Рис. 1.1. Плотность треугольного распределения

Показательное (экспоненциальное) распределение. Случайная величина X имеет показательное (экспоненциальное) распределе­ние с параметром λ(λ> 0), если ее плотность вероятности вычисляет­ся по формуле

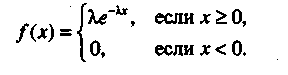
Для этой случайной величины MX = 1/ λ , DX = 1/ λ²; ее функция распреде­ления вычисляется по простой формуле F(u) = 1 - е^λu (u > 0). Эта распределение часто встречается в моделировании случайных процессов (оно обладает так на­зываемым свойством отсутствия последействия), рис.1.2.

Рис.1.2. Плотность показательного распределения

Нормальное распределение. Случайная величина X имеет нормальное распределение с параметрами m и σ², если ее плотность вероятности вычисляется по формуле

Для этой случайной величины MX = m, DX = σ². Нормальное распределение называют также гауссовским распределением.

Если m=0 и σ² = 1, то распределение называется стандартным нормаль­ным распределением. Линейное преобразование Y = (X - m)/σ приводит про­извольную нормально распределенную величину X к стандартному нормально­му распределению, показанному на рис. 1.3.

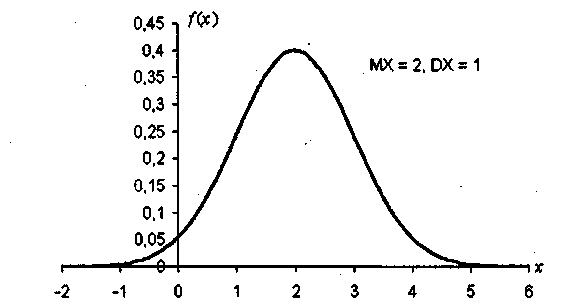
Рис.1.3. Плотность нормального распределения

Фундаментальная роль, которую играет нормальное распределение в теории вероятностей и математической статистике, объясняется тем, что при достаточно широких условиях распределение суммы случайных величин с ростом числа слагаемых асимптотически сходится к нормальному (центральная предельная теорема теории ве­роятностей).

Нормально распределенная случайная величина с большой вероятностью при­нимает значения, близкие к своему математическому ожиданию.

На ЭВМ невозможно получить идеальную последовательность случайных чисел хотя бы потому, что на ней можно оперировать только с конечным множеством чисел. Кроме того, для получения значений х случайной величины ζ используются формулы (алгорит­мы). Поэтому такие последовательности, являющиеся по своей сути детерминированными, называются псевдослучайными.

Полу­ченные с помощью генератора псевдослучайные последовательности чисел должны состоять из квазиравномерно распределенных чисел, содержать статистически независимые числа, быть воспроизводимыми, иметь неповторяющиеся числа, получать­ся с минимальными затратами машинного времени, занимать минимальный объем машинной памяти.

Моделирование случайных величин с помощью компьютера основано на преобразовании случайных чисел, имеющих равномерное распределение на интервале [0, 1] в случайные величины, имеющие другие распределения.

Получение случайных чисел, имеющих равномерное распределение на интервале [0, 1] возможно различными способами.

Мультипликативный способ заключается в следующем: если r_i = 0,0040353607, то r_i+1 = {40353607·r_i }mod 1, где mod 1 означает операцию извлечения из результата только дробной части после десятичной точки. Литературные источники говорят, что числа r_i, начинают повторяться после цикла из 50 миллионов чисел, так что r_50000001= r_i. Последовательность r_i получается квазиравномерно распределенной на интервале (0, 1). Однако, наиболее часто используются стандартную функцию, имеющуюся в языках программирования. Будем называть эту функцию random().

Проверка качества последовательностей псевдослучайных чисел {x_i} на соответствие закону распределения может быть выполнена с помощью гистограмм. Интервал (x_min, x_max) разбивается на т равных частей (подинтервалов), тогда при генерации последовательности {x_i} каждое из чисел х_j с вероятностью p_j= 1/m, j= 1,2,…,m, попадает в один из подынтервалов.

Построив столбики высота которых пропорциональна количеству значений x_i, попавших в подинтервал, получим гистограмму наглядно представляющую распределение значений рассматриваемой величины.

Допустим, имеется n измерений некоторой величины х₁, х₂, ..., х_n. Для построения гистограммы выполним следующие действия.

1. Определим размах выборки х₁, х₂, ..., х_n , т.е. R = x_max - x_min

2. Интервал R делим на m равных участков (допустим ), желательно, чтобы 5<= m<=20; тогда ширина одного участка s = r/m.

3. Определим количество значений x_i , попавших в каждый из m участков. Для этого используем формулу для номера участка, в который попадает значение x_i: k:=[(x_i-x_min)/s]+1, где k - номер участка в который попадает значение x_i, s - ширина одного участка, [ ] означают, что нужно взять целую часть значения в скобках. Учтем, что применение этой формулы для x_max дает k= m + 1.

4. Строим m столбцов равной ширины, высота столбцов пропорциональна количеству значений x_i , попавших в соответствующий участок интервала.

В результате вместо n чисел получим m чисел (m<<n).

Алгоритм решения этой задачи можно представить в следующем виде (рис. 1.4).

Рассмотрим некоторые способы преобразования последовательности рав­номерно распределенных случайных чисел {х,} в последователь­ность с заданным законом распределения {y_j}.

Формула, используемая для создания генератора случайных чисел равномерно распределенных на интервале (a, b), использующая функцию random(), имеет следующий вид:

a + ( b - а)* random().

Формулы для создания генераторов случайных чисел:

• для симметричного треугольного распределения: a + ( b - а)*( random()+random())/2;

• для нормального распределений имеющего среднее значение μ, (соответствующее максимальной вероятности) и среднеквадратическое отклонение σ, (определяющее ширину или размах распределения) числа an можно получить с помощью алгоритма:

a :=0.0;

for i=1 to 12 do a := a + random()

an:= μ + (a-6.0)* σ;

• псевдослучайную последовательность, распределенную по экспоненциальному закону можно получить с помощью алгоритма:

r := log(random());

me := μ *(-r); μ – математическое ожидание.

Задание.

1. Изучить теоретический материал.

2. Написать программу, реализующую алгоритм получения случайных чисел и построения гистограммы их распределения.

3. Реализовать программное получение последовательности случайной величины: а) равномерно распределенной на заданном интервале, б) для симметричного треугольного распределения, в) для нормального распределения, г) для экспоненциального распределения.

4. С помощью гистограмм проанализировать влияние количества значений (n) на качество получаемых последовательностей.

5. Рассмотреть распределение случайных величин для нескольких вариантов размера выборки (20, 100, 300 значений).

6. Представить полученные результаты преподавателю.

Рис.1.4. Схема алгоритма получения случайных чисел и построения гистограммы их распределения (m=5).

7. Подготовить ответы на контрольные вопросы. Чем вызвана необходимость генерации случайных величин в имитационном моделировании? Как можно оценить качество псевдослучайных чисел, получаемых с помощью стандартной функции языка программирования random()? Какие исходные данные нужны для получения случайных чисел имеющих нормальное распределение, экспоненциальное распределение, симметричное треугольное распределение?