
- •«Геометрія»
- •Афінні простори. Афінні координати. Формули перетворення
- •Поняття проективного простору. Моделі проективного простору.
- •Визначення кривої в диференціальної геометрії. Елементарна, проста та загальна крива. Регулярна крива. Способи завдання кривих.
- •Дотична площина. Нормаль. Перша квадратична форма поверхні. Довжина дуги кривої на поверхні, кут між кривими.
- •Друга квадратична форма. Нормальна кривина поверхні в данному напрямку. Головні напрямки та головні кривини.
- •Приклади многовидів
«Геометрія»
-
Афінні простори. Афінні координати. Формули перетворення
афінних координат точок.



-
Площини в афінних просторах.
![]()
Плоскость
![]() определенной точкой
определенной точкой
![]() и двумя неколлинеарными векторами
и двумя неколлинеарными векторами
![]() называется множество точек аффинного
пространства
называется множество точек аффинного
пространства
![]() такое что
такое что
![]() .
.
![]() - числа (параметры)
- числа (параметры)
![]()


![]() - векторно-параметрическое
уравнение плоскости
- векторно-параметрическое
уравнение плоскости
![]() – опорная точка
– опорная точка
![]() - базисные векторы
плоскости
- базисные векторы
плоскости

![]()

![]() - общее
уравнение плоскости
- общее
уравнение плоскости
Одномерная плоскость – прямая.
Если m = n – 1, то плоскость называется гиперплоскостью.
 - параметрическое
уравнение n-мерной
плоскости
- параметрическое
уравнение n-мерной
плоскости
Если ранг = 1, то плоскости совпадают.
Если ранг матрицы = 2, то плоскости пересекаются по прямой.
Плоскости называются
параллельными,
если
![]() либо
либо
![]()
![]() (ранг
матрицы =1 ранг расширенной матрицы = 2)
(ранг
матрицы =1 ранг расширенной матрицы = 2)
Плоскости называются скрещивающимися, если они не параллельны и не имеют общих точек
-
Аксіоми скалярного множення. Евклідові векторні простори. Евклідові точково-векторні простори.


-
Кут між векторами. Ортогональні вектори. Ортонормовані базиси і прямокутні координати.





-
Векторний та мішаний добутки.


-
Прямі в афінному прсторі. Паралельні прямі. Відрізки. Просте відношення трьох точок.


-
Теорія прямих на афінній площині. Способи завдання прямої на афінній площині. Взаємне розташування двох прямих. Жмуток прямих.


-
Теорія прямих на евклідовій площині. Нормальне рівняння прямої. Відстань від точки до прямої.



-
Еліпс, гіпербола, парабола.


![]()











![]()


![]()
![]()

![]()



![]()


-
Площини у 3-вимірному афінному просторі Геометричні способи завдання площини. Взаємне розташування двох площин. Жмуток площин.
Плоскость
в трехмерном аффинном пространстве
![]() может быть задана:
может быть задана:
1) векторно параметрическим уравнением
![]() ,
где a, b –
неколлинеарные направленные векторы
плоскости,
,
где a, b –
неколлинеарные направленные векторы
плоскости,
![]() - радиус-вектор фиксированной точки
плоскости.
- радиус-вектор фиксированной точки
плоскости.
Возьмем теперь в пространстве аффинную
систему координат Охyz.
Пусть в этой системе координат точки и
векторы имеют соответствующие координаты
![]() .
Тогда в заданной системе координат
уравнения
.
Тогда в заданной системе координат
уравнения
![]() равносильные трем уравнениям для
координат:
равносильные трем уравнениям для
координат:
![]() .
Эти уравнения называются параметрическими
уравнениями плоскости.
.
Эти уравнения называются параметрическими
уравнениями плоскости.
2) общим уравнением
![]() .
.
Система уравнения или эквивалентна ее
системе
 выражает
линейную зависимость рядов матрицы
выражает
линейную зависимость рядов матрицы
 или
уравнение
или
уравнение
![]() где
где
 Уравнение можно назвать общим уравнением
плоскости, которая проходит через тоску
Уравнение можно назвать общим уравнением
плоскости, которая проходит через тоску
![]() .
.
Уравнением плоскости, которое проходит
через три точки с координатами
![]() ,
которое не лежит на одной прямой, можно
записать в виде
,
которое не лежит на одной прямой, можно
записать в виде

Пусть плоскость проходит через точки
![]() где
где
![]() .
Тогда уравнение этой плоскости можно
записать в виде
.
Тогда уравнение этой плоскости можно
записать в виде
![]() .
Это уравнение называют уравнением
плоскости в отрезках.
.
Это уравнение называют уравнением
плоскости в отрезках.
Прямая линия в пространстве может быть задана:
1) векторно параметрическим уравнением
![]() ,
где а – направленный вектор прямой,
,
где а – направленный вектор прямой,
![]() - радиус-вектор фиксированной точки
прямой.
- радиус-вектор фиксированной точки
прямой.
Если уравнение
![]() записать в аффинной системе координат,
то получим параметрическое уравнение
прямой в пространстве:
записать в аффинной системе координат,
то получим параметрическое уравнение
прямой в пространстве:
![]() .
Включением параметра параметрические
уравнения сводится к канонической
форме
.
Включением параметра параметрические
уравнения сводится к канонической
форме
![]() .
Уравнение прямой, которое проходит
через две разные точки, можно задать в
векторной форме
.
Уравнение прямой, которое проходит
через две разные точки, можно задать в
векторной форме
![]() ,
где
,
где
![]() - радиус-вектор данных точек, а
- радиус-вектор данных точек, а
![]() - их аффинные координаты.
- их аффинные координаты.
Прямую l можно задать как линию пересечения
Взаимное расположение двух плоскостей
Если
![]() ,
то они:
,
то они:
1)
пересекаются
![]()
2)
параллельны (но не совпадают)
![]()
3)
совпадают
![]()
Если
плоскости заданы уравнениями
![]() и
и
![]() то
случаи 1 - 3 имеют месло, когда:
то
случаи 1 - 3 имеют месло, когда:
1)

2)
![]()
3)
![]()
Пучок плоскостей
Если
![]()
есть ось пучка, то уравнение пучка
![]()
Существует
всего 4 способа задания плоскости
Положение
плоскости в пространстве определяется:
а)
тремя точками, не лежащими на одной
прямой линий, рис.1
б)
прямой и точкой, взятой вне прямой,
рис.2
в)
двумя пересекающимися прямыми,
рис.3
г)
двумя параллельными прямыми.
рис.4
Каждое из представленных
на рис. 1— 4 заданий плоскости может быть
преобразовано в другое из них. Например,
проведя через точки А и В (рис. 1) прямую,
мы получим задание плоскости, представленное
на рис. 2: от него мы можем пе¬рейти к
рис. 4, если через точку С проведем прямую,
параллельную прямой АВ.

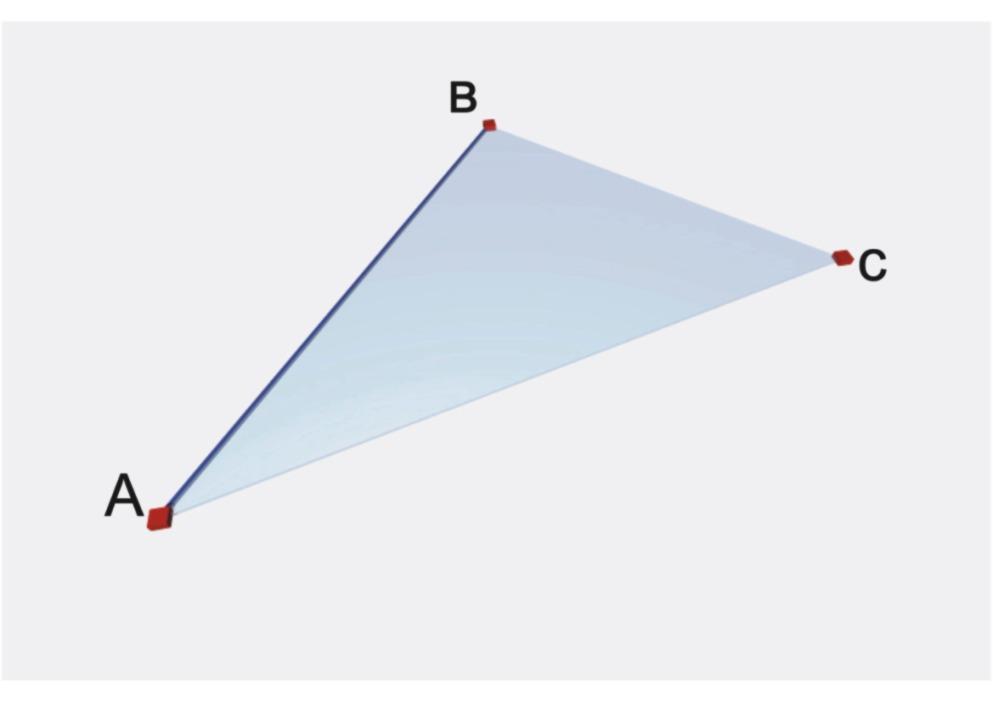

 рис.1
рис.2
рис.3
рис.4
рис.1
рис.2
рис.3
рис.4
-
Взаємне розташування прямої та площини в 3-вимірному афінному просторі
-
Взаємне розташування двох прямих в 3-вимірному афінному просторі
-
Площини у 3-вимірному евклідовому просторі.
-
Пряма у 3-вимірному афінному просторі.
-
Площина в евклідовому просторі. Нормальне рівняння площини. Відстань від точки до площини.


![]()
Пример:
![]()


![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()

-
Кут між площинами, прямими, прямою та площиною.
Кут між прямою та площиною



Кут між двома прямими в просторі



Кут між двома площинами



-
Площі та об’єми.






Фигура, составленная из касательной, главной нормали и бинормали, а также из трех плоскостей, попарно содержащих эти прямые, называют естественным трёхгранником (трёхгранником Френе
-
Поверхні обертання, еліпсоїди, гіперболоїди, параболоїди. Циліндричні та конічні поверхні (в аналітичному викладі).

Эллипсоид (рис. 4.18) Каноническое уравнение:
![]()
![]() - трехосный
эллипсоид;
- трехосный
эллипсоид;
![]() - эллипсоид вращения
вокруг оси Oz;
- эллипсоид вращения
вокруг оси Oz;
![]() - эллипсоид вращения
вокруг оси Oy;
- эллипсоид вращения
вокруг оси Oy;
![]() - эллипсоид вращения
вокруг оси Ox;
- эллипсоид вращения
вокруг оси Ox;
![]() - сфера.
- сфера.
Сечения
эллипсоида плоскостями - либо эллипс
(окружность), либо точка, либо
![]() .
.

Гіперболо́їд (грец. від hyperbole - гіпербола, і eidos - подібність) — вид поверхні другого порядку в тривимірному просторі, що задається в Декартових координатах рівнянням
![]() (Однопорожнинний
гіперболоїд),
(Однопорожнинний
гіперболоїд),
де a і b- дійсні півосі, а c- уявна піввісь;
або
![]() (двопорожнинний
гіперболоїд),
(двопорожнинний
гіперболоїд),
де a і b - уявні півосі, а c- дійсна піввісь.
Якщо a
= b,
то така поверхня зветься - гіперболоїд
обертання.
Однопорожнинний гіперболоїд обертання
можна отримати
обертанням
гіперболи
навколо її уявної осі, двополосний -
навколо дійсної. Двопорожнинний
гіперболоїд обертання також є геометричним
місцем точок
P, модуль різниці відстаней, від яких до
двох заданих точок A і B постійний:
![]() .
У такому випадку точки A і B звуться
фокусами
Гіперболоїда.
.
У такому випадку точки A і B звуться
фокусами
Гіперболоїда.
Однопорожнинний гіперболоїд є двічі лінійчатою поверхнею. Якщо він є гіперболоїдом обертання, то його можна отримати обертанням прямої навколо іншої прямої, що є мимобіжною з нею. Цю властивість лінійчатих однопорожнинних гіперболоїдів використовують в архітектурі. Зокрема, вежа Шухова в Москві є гіперболоїдною конструкцією. Вона складена саме з гіперболоїдів, що утворені прямими стрижнями.



(Однопорожнинний гіперболоїд) (двопорожнинний параболоид
гіперболоїд)
Параболо́ид ― тип поверхности второго порядка. Параболоид может быть охарактеризован как незамкнутая нецентральная (то есть не имеющая центра симметрии) поверхность второго порядка.Канонические уравнения параболоида в декартовых координатах:
![]()
-
если
 и
и
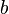 одного
знака, то параболоид называется
эллиптическим.
одного
знака, то параболоид называется
эллиптическим. -
если
 и
и
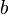 разного
знака, то параболоид называется
гиперболическим.
разного
знака, то параболоид называется
гиперболическим.
-
если один из коэффициентов равен нулю, то параболоид называется параболическим цилиндром.


-
Група перетворень подібності площини та її підгрупи.



