1. Відображення множин (функції). Область визначення функції. Монотонні функції. Парні і непарні функції. Періодичні функції.

Пусть XиYпроизвольные множества, тогдафункциейдействующей изXвYназывается некоторое правило, согласно которому каждому элементуxXставится в соответствие единственный элементyY. Функция, действующая изXвYобозначается.

Множество Xназываютобластью определения функции().

Пусть некоторая числовая функция, тогданазываетсявозрастающей (убывающей), если().

Функция, которая возрастает или убывает называется монотонной.

Функция называетсячетной (нечетной), если для любого значенияxиз области определения значение (-x) также принадлежит области определения и выполняется равенство

().

Функция называетсяпериодическойс периодом, если для любогоxиз области определения функции числаитакже принадлежат области определения и выполняется условие

.

2. Границя послідовності. Границя суми, різниці, добутку. Границя функції на нескінченності, границя функції в точці. Чудові границі .

Упорядочение значений переменной по возрастанию их номеров, приведшее к рассмотрению последовательностиэтих значений, облегчает понимание «процесса» приближения переменной- при безграничном возрастанииn– к ее пределу а. Числоaназывается пределом переменной, если для каждого положительного числа, сколько бы мало оно ни было, существует такой номерN, что все значения, у которых номерn>N, удовлетворяет неравенству(1)., переменная стремиться к а:. Число а называют также пределом последовательности, и говорят, что эта последовательность сходится к а. (1) равносильно:или. Открытый промежуток (,), с центром в точке а, принято называть окрестностью этой точки. Таким образом, какую бы малую окрестность точки а ни взять, все значения, начиная с некоторого из них, должны попасть в эту окрестность. Числоназываютпределом числовой последовательностиесли для любогонайдетсятакое что при всехвыполняется неравенство. Обозначается.

Пусть ,две последовательности такие, чтотогда. Эти свойства можно записать

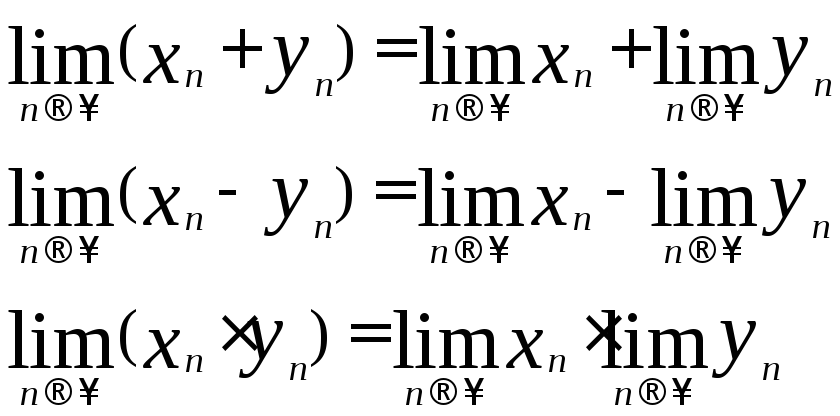
Таким образом, предел суммы= сумме пределов,предел разности= разности пределов,предел произведения= произведению пределов.

Определение (по Коши):Пусть функцияопределена на множестве, гдечислоAназывают пределом функциипри, если для любой окрестностинайдется числотакое что при всехxудовлетворяет неравенствуи выполняется включение.

Определение (по Гейне):ЧислоA– пределпри, если для любоготакой чтопоследовательностьсходится кA.

Определение (по Коши):Пусть функцияопределена в некоторой проколотой окрестностичислоAназывают пределом функциипри, еслинайдется положительное числотакое что при всехи удовлетворяющему неравенствувыполняется неравенство.

Определение (по Гейне):Пусть функцияопределена в некоторой проколотой окрестноститочки, числоAназывают пределом функциипри, если для любой последовательноститакой чтоипоследовательностьсходится к числуA.

Первый замечательный предел

Теорема 1: при ,

Второй замечательный предел

Теорема 2: существует конечный предел . Этот предел называет число, т. е.. Числоиграет важную роль в математике. Это число иррациональное.

Третий замечательный предел

Четвертый замечательный предел

Пятый замечательный предел

3. Неперервність функції. 1-а і 2-а теореми Больцано-Коши, 1-а і 2-а теореми Вейерштраса.

Определение2. Функция называется непрерывной в точке х₀ если: (2) Это определение предъявляет функции следующие требования:1) функция должна быть определена в точке х₀ и некоторой ее окрестности.2) Функция Функция должна иметь в точке х₀ предел.3) Этот предел должен совпадать со значением функции в точке х₀ . Определение 2 означает, что для непрерывности в точке х₀ функции знаки lim и f функции перестановочны, т.е. . Предел функции равен функции от предела аргумента. Если хотя бы одно из трех требований предъявляемым к функции в определении 2 не выполняется, то говорят, что функция разрывна в т. х₀ или имеет в т. х₀ разрыв; при этом предполагается, что функция определена в некоторой окрестности кроме быть может т. х₀. Тогда т. х₀ - называется точкой разрыва функции . Определение 2 аналитически выражает интуитивное представление о непрерывности графика функции т.е. кривой .

Первая теорема Больцано-Коши: Пусть функция определена и непрерывна в замкнутом промежуткеи на концах этого промежутка принимает значения разных знаков. Тогда между а иbнеобходимо найдется точка с, в которой функция обращается в нуль:(a<c<b). геометрический смысл: если непрерывная кривая переходит с одной стороны оси х на другую, то она пересекает эту ось.

Доказательство. (по методу деления промежутка). Для определенности положим, что ,a. Разделим промежутокпополам точкой. может случиться, что функцияобратиться в нуль в этой точке, тогда теорема доказана: можно положить. пусть также, тогда на концах одного из промежутковфункция будет принимать значения разных знаков(и притом отрицательное значение на левом конце и положительное – на правом). Обозначив этот промежуток через, имеем. Разделим пополам промежутоки снова отбросим тот случай, когдаобращается в нуль

В середине этого промежутка, ибо тогда теорема доказана. Обозначим черезту из половин промежутка, для которой0.

Продолжим этот процесс построения промежутков. При этом либо мы после конечного числа шагов наткнемся в качестве точки деления на точку, где функция обращается в нуль, и док-во завершится, либо получим бесконечную последовательность вложенных один в другой промежутков. Тогда для k-го промежутка , k∈N будем иметь0 (1), причем длина его, очевидно, равна(2)_.

Построенная последовательность промежутков удовлетворяет условиям леммы о вложенных промежутках, ибо, ввиду (2), поэтому обе переменныеистремятся к общему пределу., который очевидно, принадлежит.Покажем, что именно эта точка удовлетворяет требованию теоремы. Переходя к пределу в неравенствах (1) и используя при этом непрерывность функции (в точке х=с), получим, чтотак что действительно.

Вторая теорема Больцано – Коши.Пусть функцияопределена и непрерывна в замкнутом промежуткеи на концах этого промежутка принимает не равные значения f(a)=A и f(b)=В. Тогда, каково бы ни было число C, лежащее между А и В, найдется такая точка c междуaиb, что f(c)=C.

Доказательство:Основано на первой теореме Больцано-Коши.

Будем считать, например, А<B, так чтоA<C<B. рассмотрим на промежуткевспомогательную функцию φ(x)=f(x)−C она непрерывна в промежутке и на концах его имеет разные знаки:(b)=f(b)−C=B−C>0, :(a)=f(a)−C=A−C<0, тогда по первой теореме между a и b найдется точка с, такая что(c)=0, т.е. f(c)-C=0 или f(c)=C. ч.т.д.

Геометрический смысл этой теоремы: всякая прямая y=C, где B<C<A, пересечет график функции f по крайней мере в одной точке.

Замечание. Если f - непрерывна и непостоянна на I, то образом этого промежутка I при отображении f будет также промежуток (т.е. непрерывным образ f(I)промежутка I есть промежуток). В самом деле, по теореме из того, что B,A∈E(f)следует, что интервал (B;A)⊂E(f), т.е. E(f)⊂f(I)- промежуток.

Первая теорема Вейерштрасса.

Если функция определена и непрерывна в замкнутом промежутке, то она ограничена и знизу и сверху, т.е. существуют такие постоянные и конечные числаmи М, чтопри.

Доказательство: методом от противного,допустим, что функцияпри изменении х в промежуткеоказывается неограниченной, скажем, сверху. В таком случае для каждого натурального числаn найдется в промежуткетакое значение х=х_n, чтоf(x_n)n.(3)

По лемме Больцано-Вейерштрасса, из последовательности ,сходящуюся к конечному пределу: (при ) , причем, очевидно, . Вследствие непрерывности функции в точке, тогда должно быть и, а это не возможно, так как из (3) следует, что. Получено противоречие. Теорема доказана.

Вторая теорема Вейерштрасса.

Если функция определена и непрерывна в замкнутом промежутке, то она достигает в этом промежутке своих точных верхней и нижней границ. Иными словами, в промежуткенайдутся такие точки х₀и х₁, что значенияи, будут, соответственно, наибольшим и наименьшим из всех значений функции.

Доказательство. Положим, по предыдущей теореме, это – число конечное. Предположим, что всегда<M, т.е., что граница М не достигается. В таком случае, можно рассмотреть вспомогательную функцию. Так как , по предположению, знаменатель здесь в нуль не обращается, то эта функция будет непрерывна, а следовательно (по предыдущей теореме), ограничена:. Но тогда легко получить, что тогда<M-, т.е. числоM-, меньше чем М, оказывается верхней границей для значений функции, чего быть не может, ибо М есть точная верхняя граница этих значений. Полученное противоречие доказывает теорему: в промежуткенайдется такое значение, чтобудет наибольшим из всех значений. Аналогично может быть доказано утверждение и относительно наименьшего значения.