- •Гл. Yi. Основные теоремы и некоторые применения дифференциального исчисления. § 1. Теоремы о среднем
- •§ 2. Достаточные условия монотонности и экстремума функции на промежутке
- •§ 3. Выпуклость, точки перегиба и асимптоты графика функции
- •§ 4. Примерная схема исследования графика функции
- •§ 5. Правило Лопиталя
- •§ 6. Формулы Тейлора и Маклорена и некоторые их применения
- •I. Представление некоторых функций формулой Маклорена ():
§ 3. Выпуклость, точки перегиба и асимптоты графика функции
Пусть функция
![]() непрерывна в интервале
непрерывна в интервале![]() и
дифференцируема в точке
и
дифференцируема в точке![]() .
Рассмотрим взаимное расположение
графика функции и его касательной в
точке
.
Рассмотрим взаимное расположение
графика функции и его касательной в
точке![]() ,
уравнение которой имеет вид
,
уравнение которой имеет вид![]() .
.
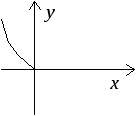
Определение1. Точка![]() называетсяточкой выпуклости вверх
(вниз), если
называетсяточкой выпуклости вверх
(вниз), если![]() ,
в которой
,
в которой![]()
![]() ,
т.е. график функции
,
т.е. график функции![]() в окрестности
в окрестности![]() лежит
ниже (выше) своей касательной в точке
лежит
ниже (выше) своей касательной в точке![]() .
.
Определение 2. Если каждая точка
интервала![]() есть
точка выпуклости вверх (вниз) для графика
функции
есть
точка выпуклости вверх (вниз) для графика
функции![]() ,
то функция
,
то функция![]() называетсявыпуклой вверх (вниз) на
интервале
называетсявыпуклой вверх (вниз) на
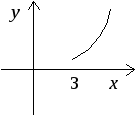
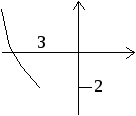
интервале![]() (рис. 1 а,б).
(рис. 1 а,б).
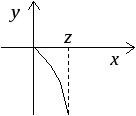
а)
б) в)
Рис. 1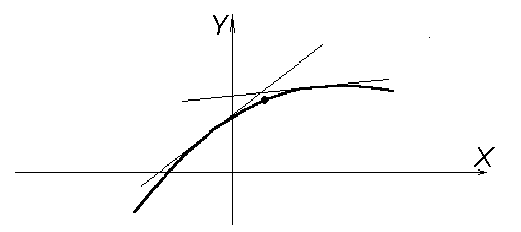


Определение3. Точка![]() называетсяточкой перегибаграфика
функции
называетсяточкой перегибаграфика
функции![]() ,
если при переходе через нее график
меняет направление выпуклости (рис. 1
в).
,
если при переходе через нее график
меняет направление выпуклости (рис. 1
в).
Исходя из приведенных определений, достаточное условие выпуклости и перегиба графика функции можно выразить через первую производную (см. упр. 1). Однако мы ограничимся следующим утверждением.
Теорема1. Пусть функция![]() дважды
дифференцируема в интервале
дважды
дифференцируема в интервале![]() .
Тогда, если
.
Тогда, если![]()
![]() в
в![]() ,
то функция
,
то функция![]() выпукла
вниз (выпукла вверх) на
выпукла
вниз (выпукла вверх) на![]() ;
если функция
;
если функция![]() меняет знак при переходе через точку
меняет знак при переходе через точку![]() ,
то
,
то![]() - точка перегиба.
- точка перегиба.
Доказательство. Пусть![]() - касательная к графику функции
- касательная к графику функции![]() в точке
в точке![]() .
Тогда по теореме Лагранжа получим
.
Тогда по теореме Лагранжа получим
![]()
![]()
где
![]() и точка
и точка![]() лежит между
лежит между![]() и
и![]() .
.
Применим еще раз теорему Лагранжа к
функции
![]() ,
получим
,
получим
![]()
где точка
![]() лежит
между точками
лежит
между точками![]() и
и![]() .
.
П оскольку
точки
оскольку
точки![]() и
и![]()
![]() лежат по одну сторону от точки
лежат по одну сторону от точки![]() ,
то
,
то![]() .
В силу этого знак разности
.
В силу этого знак разности![]() при
при![]() совпадает со знаком
совпадает со знаком![]() ,
откуда и следует утверждение теоремы.
,
откуда и следует утверждение теоремы.
Вставка 1.
Определение4. Говорят, что прямая![]() являетсявертикальной асимптотойграфика функции
являетсявертикальной асимптотойграфика функции![]() ,
если хотя бы одно из предельных значений
,
если хотя бы одно из предельных значений![]() или
или![]() равно
равно![]() или
или![]()
Из этого определения видно, что если
![]() есть
точка бесконечного разрыва функции
есть
точка бесконечного разрыва функции![]() ,
то прямая
,
то прямая![]() есть вертикальная асимптота для графика
функции
есть вертикальная асимптота для графика
функции![]() .
Верно и обратное.
.
Верно и обратное.
Определение5. Пусть![]() ,
либо
,
либо![]() ,
либо
,
либо![]() .
Прямая
.
Прямая![]() называетсянаклонной асимптотойграфика функции
называетсянаклонной асимптотойграфика функции![]() ,
если
,
если![]() .
.
Теорема2 (нахождение наклонной
асимптоты). Условие![]() эквивалентно паре условий
эквивалентно паре условий![]()
![]() .
.
Доказательство. 1)![]() .
Из левого равенства получим
.
Из левого равенства получим![]() ,
из правого -
,
из правого -![]() ,
что равносильно равенству
,
что равносильно равенству![]() .
.
Непосредственно из соотношения
 получим
получим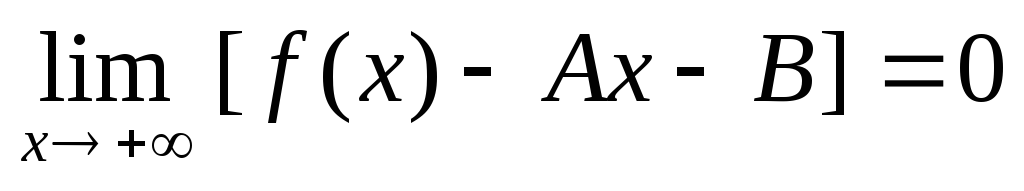 .
.
Вставка 2.
Вопросы и упражнения
1.Доказать утверждение:"Пусть
функция![]() дифференцируема
в интервале
дифференцируема
в интервале![]() .
Тогда, если
.
Тогда, если![]() возрастает (убывает) на
возрастает (убывает) на![]() ,
то функция
,
то функция![]() выпукла
вниз (вверх)".
выпукла
вниз (вверх)".
2.Доказать, что если функция![]() непрерывна
на интервале
непрерывна
на интервале![]() и
если
и
если![]()
![]() выполняется неравенство
выполняется неравенство![]() ,
то функция
,
то функция![]() выпукла
вверх (вниз) на интервале
выпукла
вверх (вниз) на интервале![]() .
Дать геометрическое толкование этого
неравенства.
.
Дать геометрическое толкование этого
неравенства.
3.Доказать неравенство![]()
![]() .
.
§ 4. Примерная схема исследования графика функции
Можно порекомендовать следующую схему исследования:
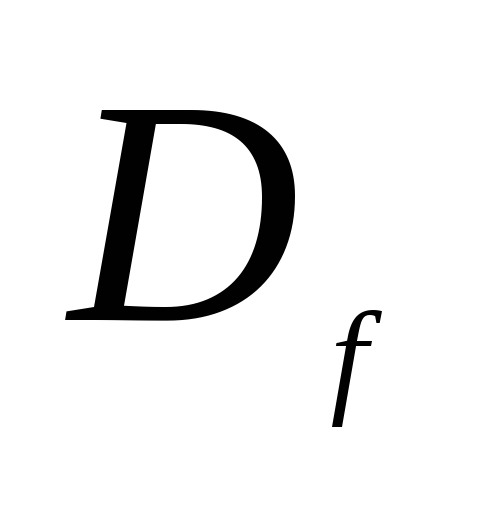 ,
точки разрыва и их характер, вертикальные
асимптоты.
,
точки разрыва и их характер, вертикальные
асимптоты.Симметрия графика: четность, нечетность, периодичность; точки пересечения с осями координат.
Наклонные асимптоты.
Использование первой производной: промежутки монотонности, локальные экстремумы.
Использование второй производной: интервалы выпуклости, точки перегиба, контроль локального экстремума.
Составление сводной таблицы.
Построение графика.
В случае необходимости можно определить еще несколько точек графика.
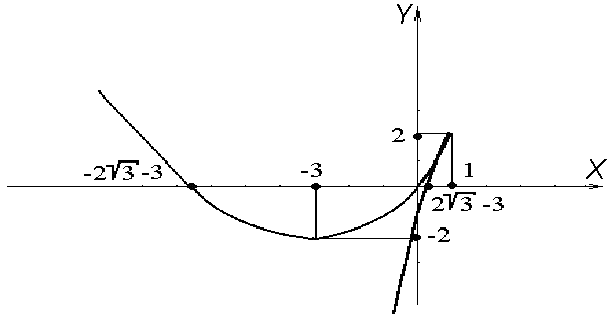
Пример 1.Исследовать и построить
график функции![]() .
.
Решение. 1)![]() ,
,![]()
![]()
![]() - вертикальная асимптота.
- вертикальная асимптота.
График симметрией не обладает. Точки пересечения с осями координат: (0, 0).
 наклонных асимптот нет.
наклонных асимптот нет.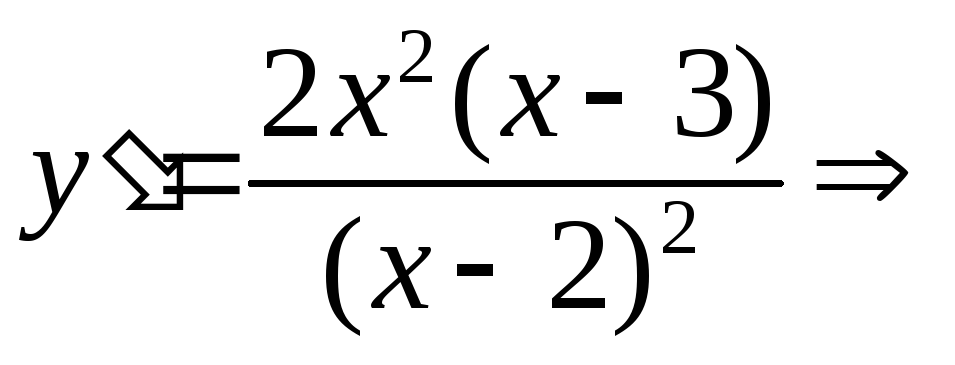

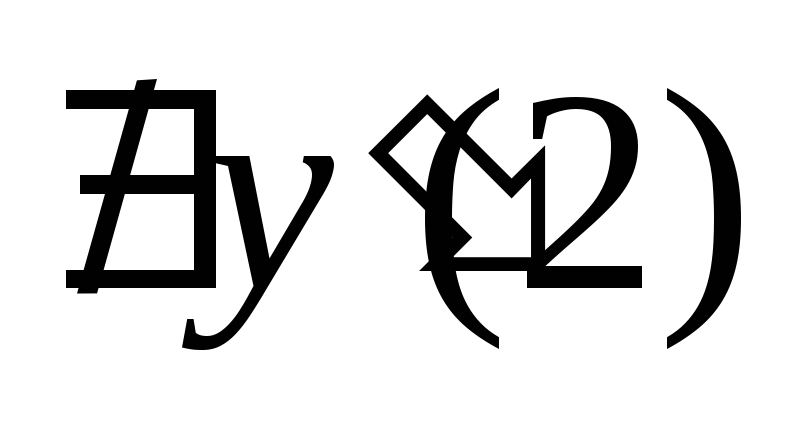 ;
;
![]() при
при![]() и
и![]() при
при![]()
![]()
![]() - точка локального минимума.
- точка локального минимума.
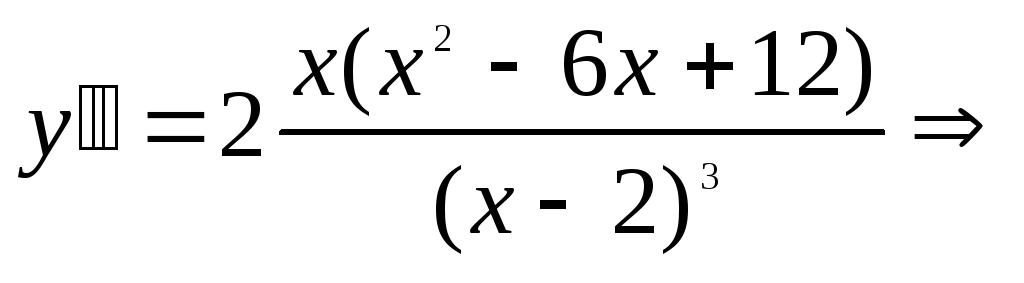
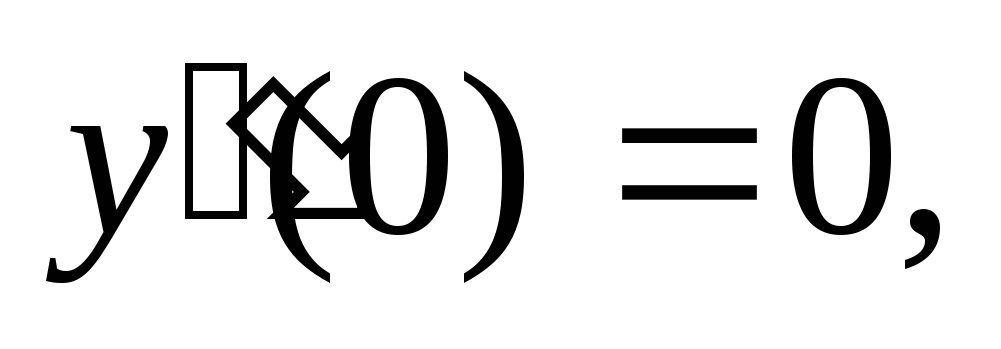
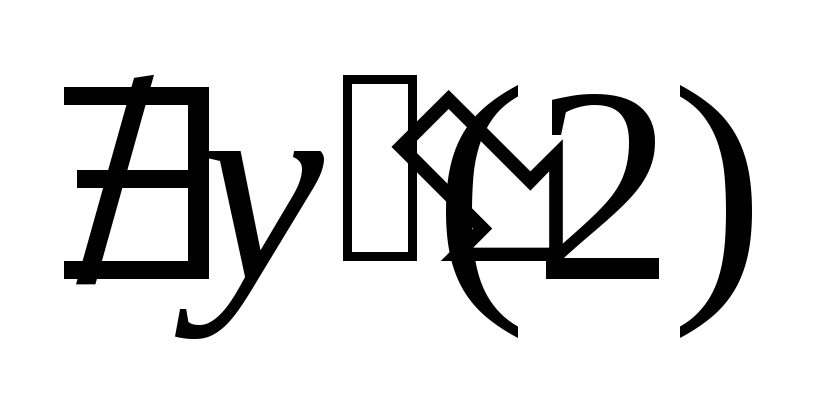 ;
;
![]() при
при![]() и
и![]() при
при![]() - точка перегиба.
- точка перегиба.
|
x |
y |
|
|
Эскиз | |
|
|
|
– |
+ |
| |
|
0 |
0 |
0 |
0 | ||
|
(0, 2)
|
|
– |
– |
| |
|
2 |
не опр. |
не опр. |
не опр. | ||
|
(2, 3)
|
|
– |
+ |
| |
|
3 |
27 |
0 |
+ | ||
|
|
|
+ |
+ |
| |
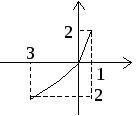
Таким образом, график функции
![]() имеет вид (рис. 2).
имеет вид (рис. 2).

Рис.2
Пример 2.![]() .
.
Решение.1)![]() и
и![]() определены
и непрерывны
определены
и непрерывны![]() ,
причем
,
причем![]() ,
,![]() .
Следовательно, функция
.
Следовательно, функция![]() определена при
определена при![]() .
Вертикальных асимптот нет, т.к.
.
Вертикальных асимптот нет, т.к.![]() непрерывна
как суперпозиция непрерывных функций.
непрерывна
как суперпозиция непрерывных функций.
2) График функции
![]() не обладает симметрией, т.к. ее область
определения не симметрична. Точки
пересечения с осями координат: (0, 0),
(0, -2),
не обладает симметрией, т.к. ее область
определения не симметрична. Точки
пересечения с осями координат: (0, 0),
(0, -2),![]() ,
,![]() .
.
3) Так как при
![]()
![]()
![]()
![]() то наклонных асимптот нет.
то наклонных асимптот нет.
4) ![]()
![]() при
при![]()
![]() ,
при
,
при![]()
![]() у функции
у функции![]() устранимый разрыв;
устранимый разрыв;![]() при
при![]()
![]() ,
,![]() при
при![]()
![]() .
.
5) ![]()
![]() при
при![]()
![]() ;
;![]() при
при![]()
![]() ,
,![]() при
при![]()
![]() .
.
|
t |
x |
y(x) |
|
|
Эскиз |
|
|
|
|
– |
+ |
|
|
–1
|
–3 |
–2 |
0 |
+ | |
|
(–1, 1)
|
(–3, 1) |
(–2, 2) |
+ |
+ |
|
|
1
|
1 |
2 |
|
| |
|
|
|
|
+ |
–
|
|
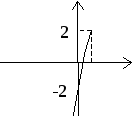
Таким образом, получим график (рис. 3).
Рис. 3