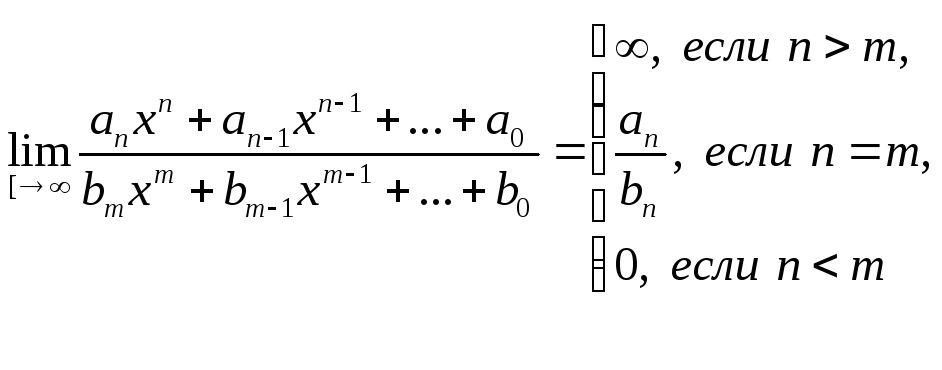§ 3. Свойства пределов функции.
Лемма(о сохранении знака функции,
имеющей предел). Если![]() ,
то> 0:
,
то> 0:![]() sgnf(x)
=sgna.
sgnf(x)
=sgna.
Доказательство.Пусть, для
определенности,а > 0. Возьмем
= а. По определению предела (по Коши)=()
> 0:![]() |f(x)
–a| <a
и, следовательно, верно неравенствоf(x)
–a> -a,
откудаf(x)> 0
|f(x)
–a| <a
и, следовательно, верно неравенствоf(x)
–a> -a,
откудаf(x)> 0![]() .
.
В случае а< 0 следует взять = - а.
Теорема1 (арифметические свойства
пределов). Пусть функцииfиgопределены на
множествеDих0– точка сгущенияD.
Если![]() ,
,![]() ,
то :
,
то :
1)
![]() ;
;
2)
![]() ;
;
3)
![]() (приb0).
(приb0).
Доказательство.Воспользуемся определением предела по Гейне и соответствующими теоремами о пределах последовательностей.
Пусть {xn}D\{x0}
– произвольная последовательность.
Тогда по условию теоремы![]() .
Поэтому
.
Поэтому
1 - 2)
![]() .
.
Аналогично,
![]() .
.
В виду произвола последовательности {xn} получим 1) и 2).
3) Для доказательства предела частного воспользуемся леммой. Так как b0, то функцияg отлична от нуля в некоторой окрестностиО(х0). Поэтому, требуя дополнительно, чтобы {xn}О(х0), получим
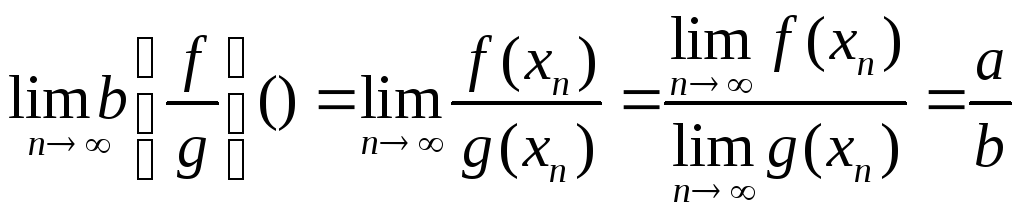 .
.
А т.к. последовательности {xn} – произвольная, то верно 3).
Следствие.Пусть![]() ,СRиr Q. Тогда:
,СRиr Q. Тогда:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() .
.
Вставка 1.
Теорема 2. Пустьf(x)0
(f(x)0) для всеххиз
некоторой проколотой окрестности точких0, причем![]() .
Тогдаа0 (а0).
.
Тогдаа0 (а0).
Доказательство. Предположим, чтоа< 0. Тогда по лемме в некоторой проколотой окрестности точких0имеет место неравенствоf(x) < 0, что противоречит условию теоремы.
Следствие.Пустьf(x)g(x)
для всехх из некоторой проколотой
окрестности точких0(![]() ),
причем
),
причем![]() и
и![]() . Тогдааb.
. Тогдааb.
Доказательство.Положим(х)
=f(x)
-g(x).
Тогда(х)0х![]() .
По теореме 1
.
По теореме 1![]() .
Тогда по теореме 2a
–b0, т.е.а b.
.
Тогда по теореме 2a
–b0, т.е.а b.
Определение 1. Функцияfназывается ограниченной сверху (ограниченной снизу, ограниченной) на множествеEDf, если множествоf(E) ограничено сверху (ограничено снизу, ограничено).
Теорема 3(о локальной ограниченности
функции, имеющей предел). Если![]() ,
то функцияfограничена
в некоторой окрестности точких0.
,
то функцияfограничена
в некоторой окрестности точких0.
Доказательство. Пусть![]() .
Тогда по определению предела функции
в точке (по Коши), например, для= 1> 0:
.
Тогда по определению предела функции
в точке (по Коши), например, для= 1> 0:![]() ,
откуда |f(x)|
< |a| + 1, что и означает
ограниченность функцииfв
,
откуда |f(x)|
< |a| + 1, что и означает
ограниченность функцииfв![]() .
.
Определение2. Функцияназываетсябесконечно малой (б/м)
прихх0,
если![]() .
.
Определение3. ФункцияFназываетсябесконечно большой (б/б)
прихх0,
если![]() ,
т.е. (по Гейне){xn}DF\{x0},
,
т.е. (по Гейне){xn}DF\{x0},![]() ,последовательность
{F(xn)}
-б/б (
,последовательность
{F(xn)}
-б/б (![]() ).
).
Теорема 4. 1) Если-б/м функция прих х0, причем(х)0, то![]() -б/б функция прихх0.
-б/б функция прихх0.
2) Если F-б/б функция
прих х0,
то![]() -б/м функция прихх0.
-б/м функция прихх0.
Доказательствонепосредственно следует из определения предела функции в точке по Гейне и соответствующей теоремы дляб/м иб/б последовательностей.
Аналогично получим
Теорема 5. 1) Сумма конечного числаб/м прих х0функций есть функцияб/м прихх0;
2) Произведение б/м прихх0функции и ограниченной в![]() функции есть
функции есть
функция б/м прих х0;
3) Произведение любого числа б/м прих х0функций есть функцияб/м прих х0;
4) Частное от деления ограниченной в
![]() функции иб/б прихх0функции есть функцияб/м
прих х0.
функции иб/б прихх0функции есть функцияб/м
прих х0.
Вставка 2.
Вопросы и упражнения.
Показать, что все свойства пределов остаются верными и для односторонних пределов.
Показать, что если f(x)>g(x)x
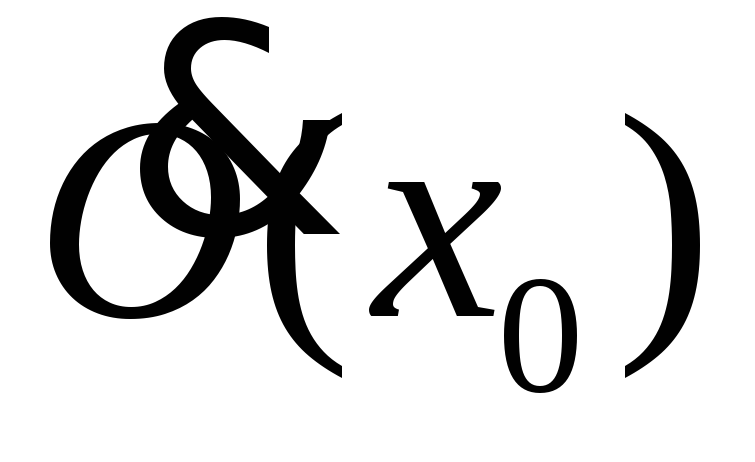 и
и ,
тоab.
,
тоab.Пусть
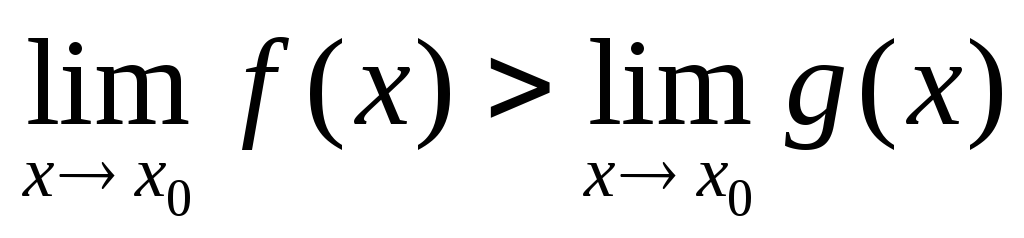 .
Доказать, чтоО(х0):x
.
Доказать, чтоО(х0):x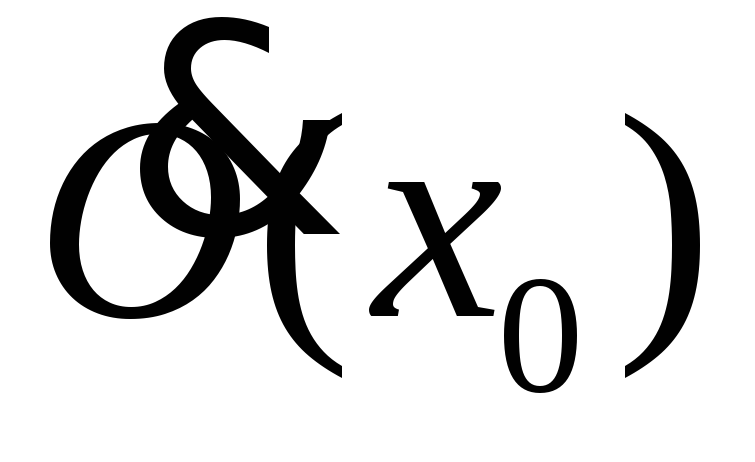 f(x)
>g(x).
f(x)
>g(x).Дать определение ограниченной снизу (ограниченной сверху, ограниченной) функции на множестве Е Dfчерез неравенства.
Сформулировать определение неограниченной снизу (неограниченной сверху, неограниченной) функции на множестве.
Доказать, что если функция F-б/бприхх0, аgограничена в
 ,
то функцияF
g-б/бприхх0.
,
то функцияF
g-б/бприхх0.Доказать ограниченность функции
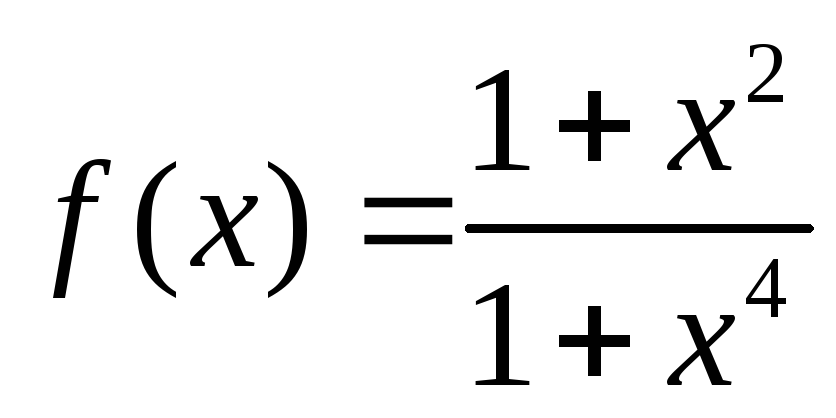 на всей числовой оси.
на всей числовой оси.Дать определение по Коши б/бфункции прихх0.
Доказать, что сумма б/бфункций прихх0одного знака естьб/бфункция прихх0 того же знака.
Установить связь между неограниченной и б/бфункциями. Рассмотреть функцию
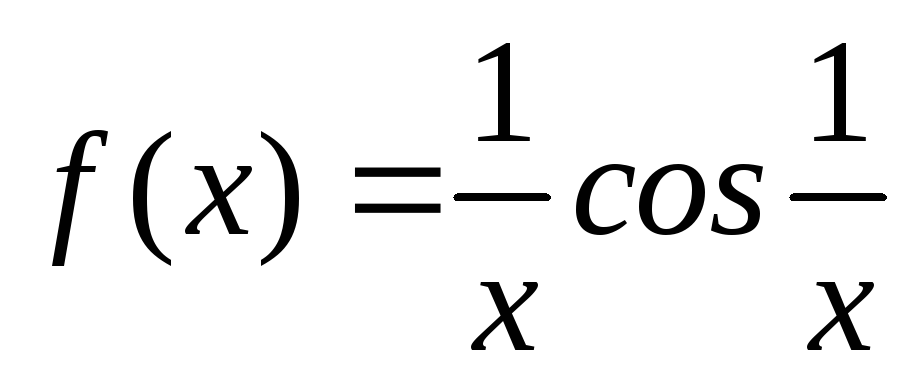 вО(0).
вО(0).Доказать, что: а)
 ;
;
б)