
- •3 4, І так далі, і насамкінець, матриця має розмір 100 101. З’ясувати, які з поданих добутків є визначеними. Указати кількості рядків і стовпців для тих добутків, що є визначеними.
- •4. Обернена матриця
- •Відповіді
- •Л) . 3.38. A–1 існує тоді і тільки тоді, коли всі ai, ≠ 0, 1 I n,
- •Рекомендована література
Аналогічно
вводиться операція віднімання.
Різницею
двох матриць
![]() і
і
![]() називається матриця
називається матриця
![]() ,
елементи якої визначаються за правилом
,
елементи якої визначаються за правилом
![]() (
1
i
k,
1
j
n).
(
1
i
k,
1
j
n).
Приклад
3.1.
Нехай
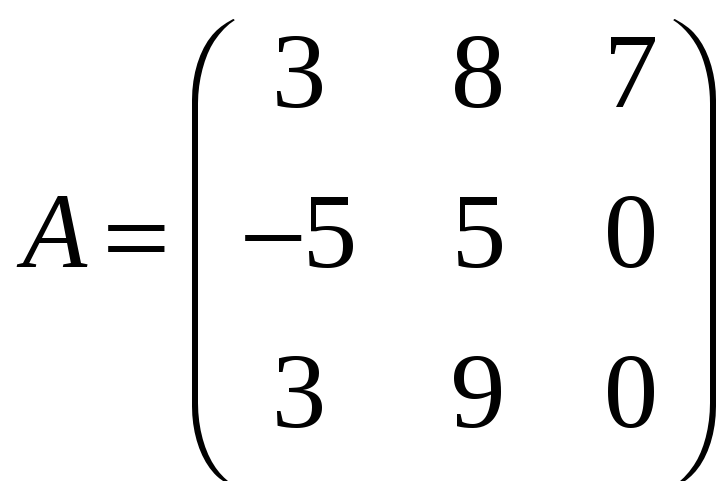 ,
,
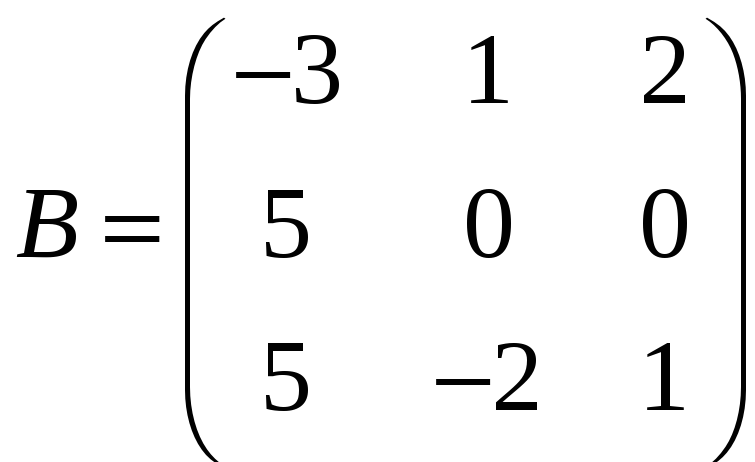 .
Знайдемо матриці A
+ B
і A
– B.
.
Знайдемо матриці A
+ B
і A
– B.
A
+ B
=
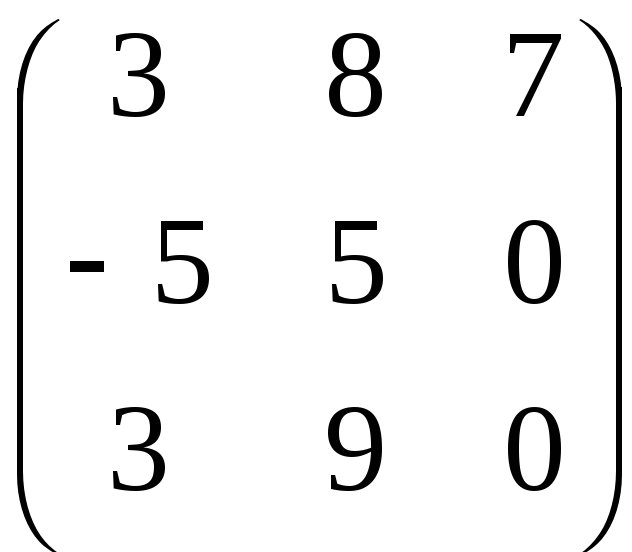 +
+
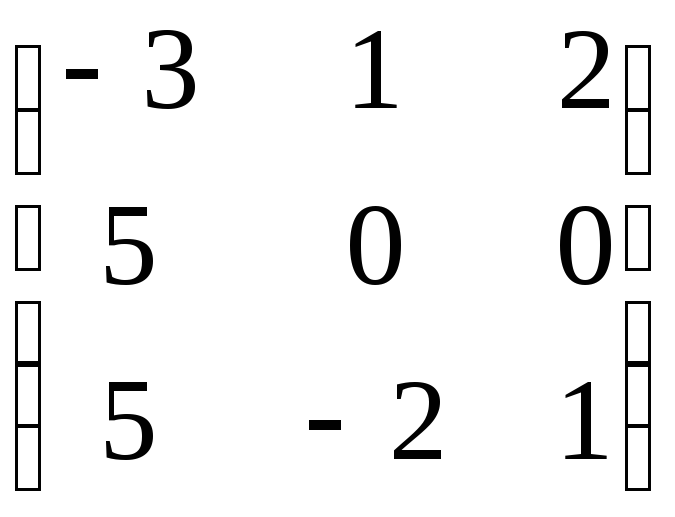 =
=
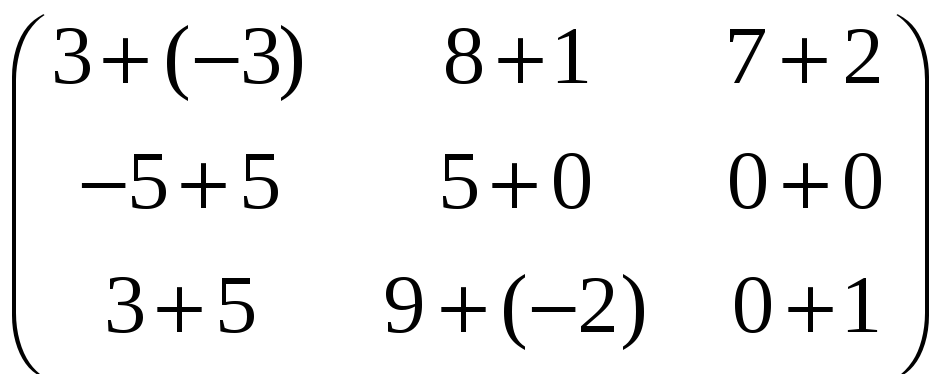 =
=
 .
.
A
– B
=
 –
–
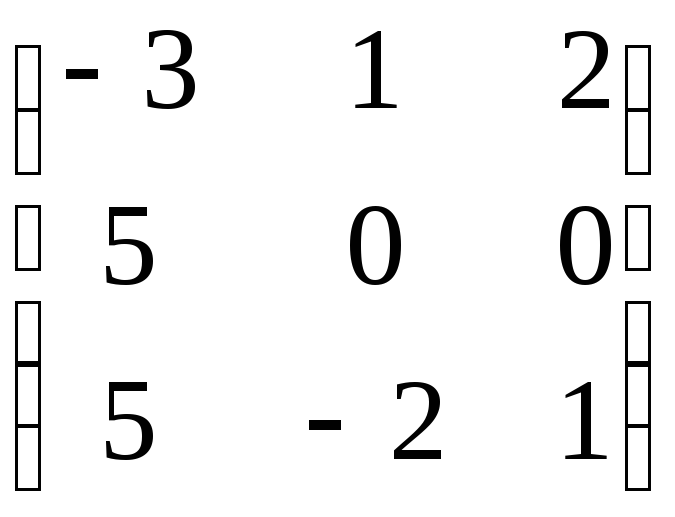 =
=
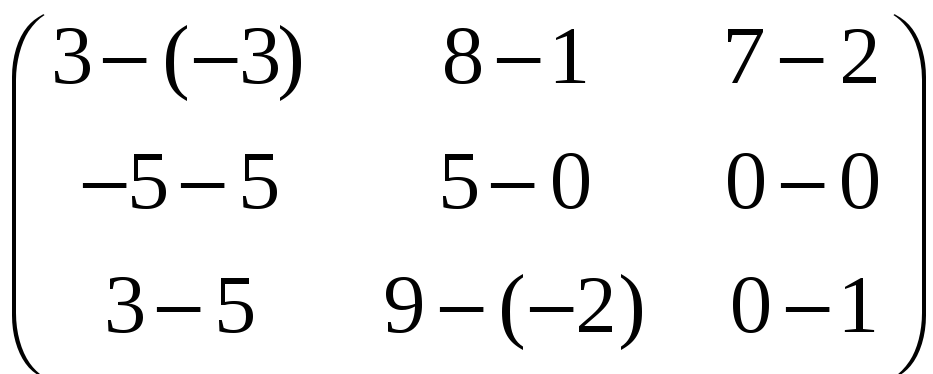 =
=
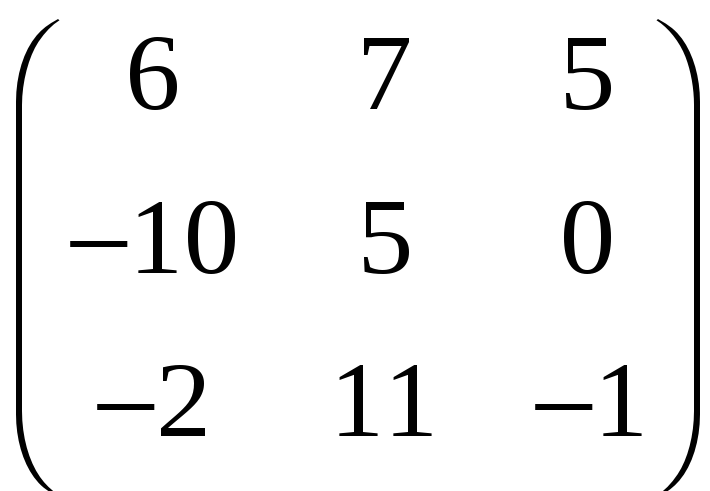 .
.
З означення додавання матриць випливають такі властивості цієї операції:
1. А + В = В + А (комутативність додавання);
2. (А + В) + С = А + (В + С) (асоціативність додавання);
3. Матриця 0, кожен елемент якої дорівнює нулю, відіграє роль нуля: A + 0 = A для будь-якої матриці A того ж розміру, що і 0;
4. Для будь-якої квадратної матриці А існує так звана протилежна матриця, яка позначається (А), тобто така, що
А + (А) = 0.
Для кожної матриці А протилежна матриця єдина і, очевидно, є матрицею з елементами, протилежними до відповідних елементів A.
Нехай
![]() ,
R.
Добутком
числа
та матриці
А
називається матриця А
=
,
R.
Добутком
числа
та матриці
А
називається матриця А
=
![]() ,
елементи якої визначаються за правилом
,
елементи якої визначаються за правилом
![]() (1
i
k,
1
j
n).
(1
i
k,
1
j
n).
Інакше кажучи, щоб помножити число на матрицю, необхідно помножити кожен її елемент на це число.
Приклад
3.2.
Знайдемо добуток 3A,
якщо
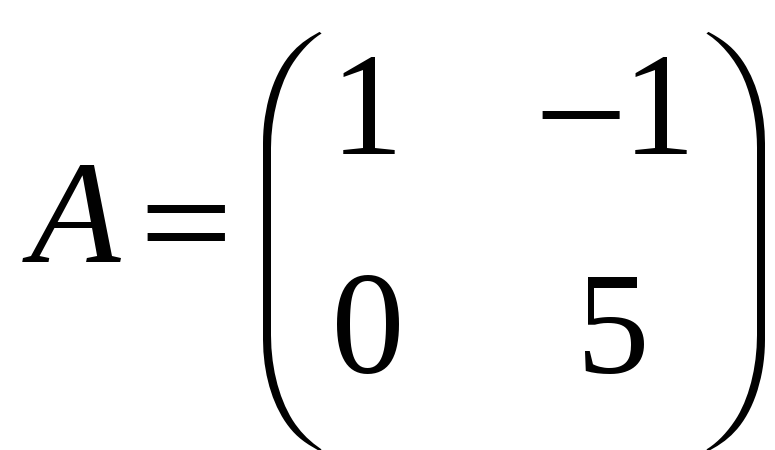 .
.
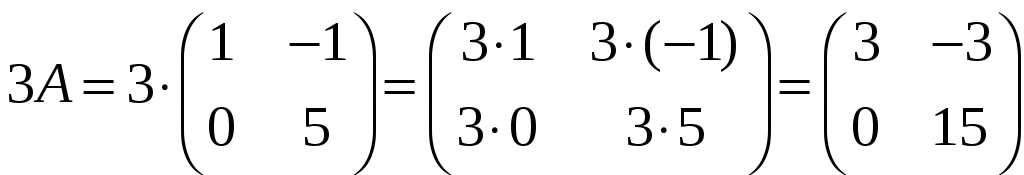 .
.
Операція множення матриці на число має такі властивості:
1. 1А = А.
2. (А) = ()А = (А).
3. ( + )А = А + А.
4. (А + В) = А + В.
Приклад 3.3. Задано три матриці:
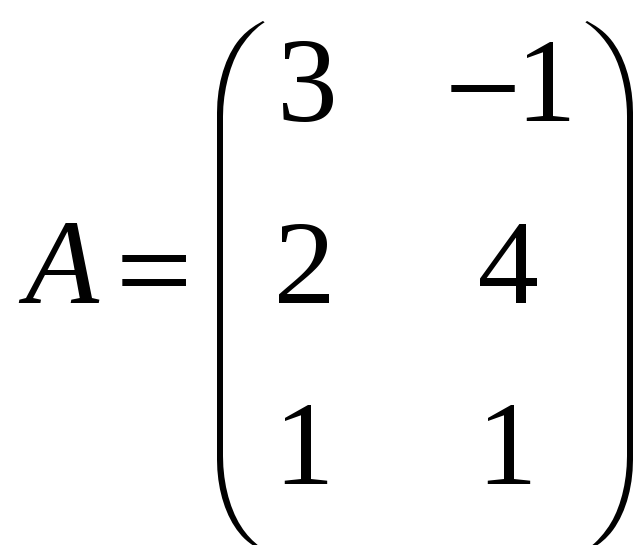 ,
,
 ,
,
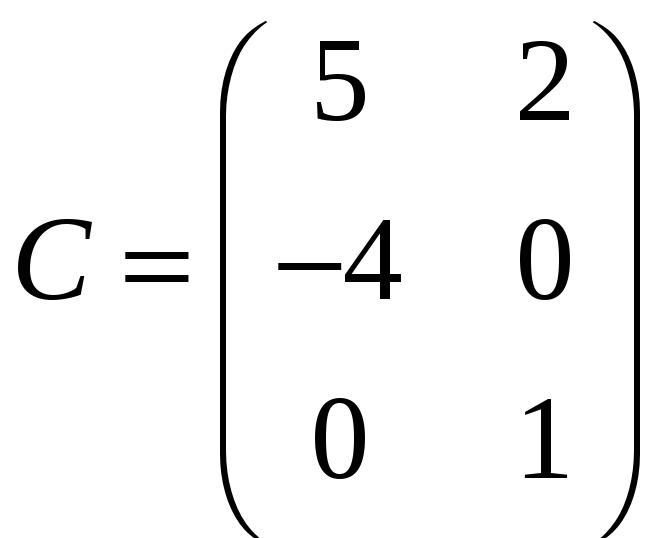 .
.
Знайдемо матрицю D = 2A – 3B + 6C
За означенням добутку матриці на число, одержимо:
 ,
,
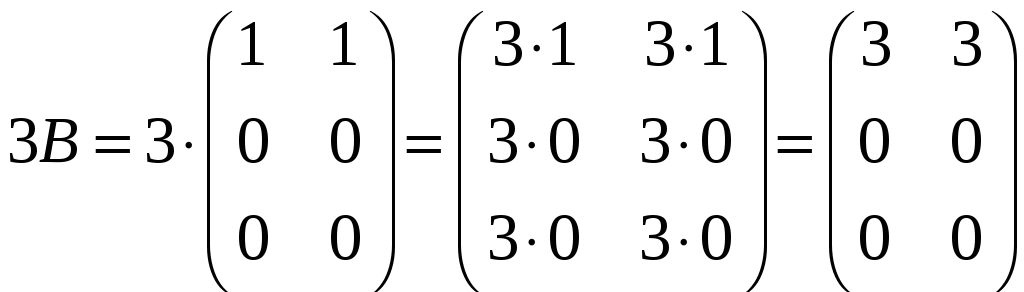 ,
,
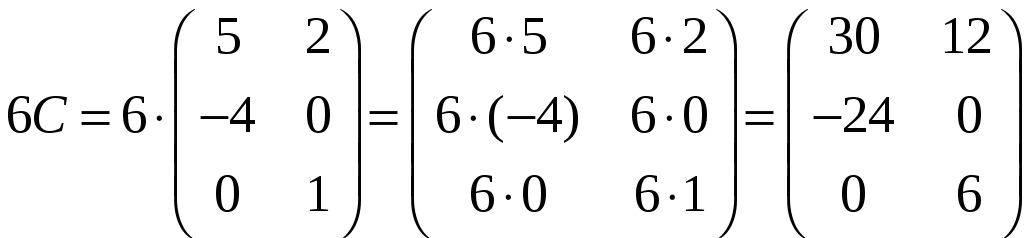 .
.
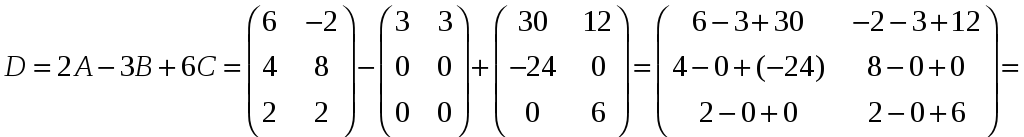
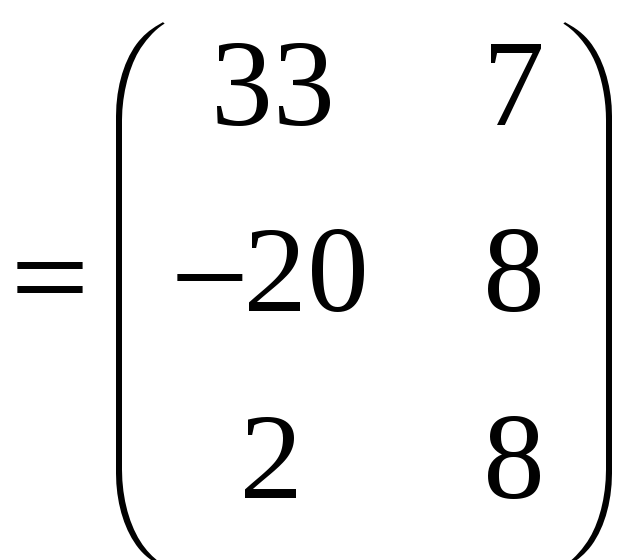 .
.
Задача 3.1. Задано матриці:
 ,
,
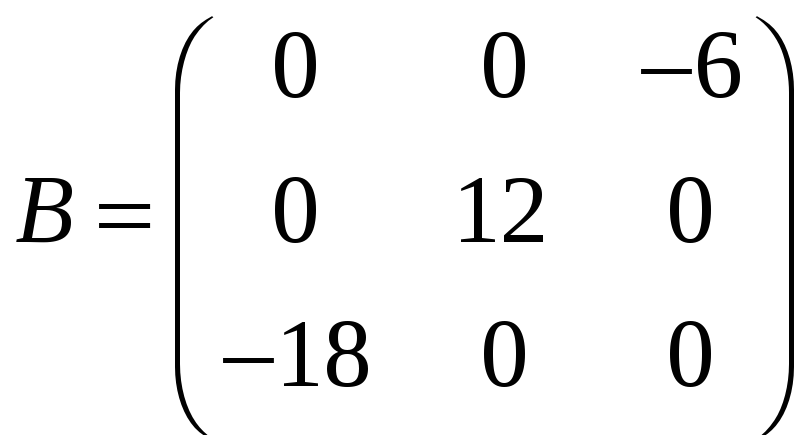 ,
,
 .
.
Знайти:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Задача 3.2. Знайти матрицю X, якщо:
а)
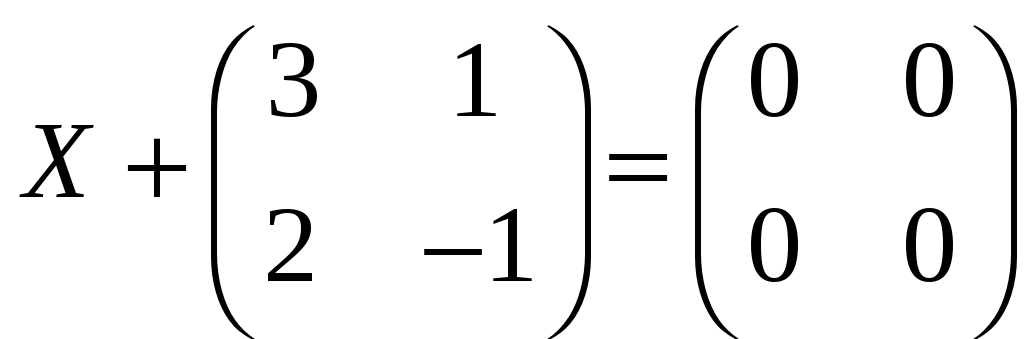 ;
б)
;
б)
 ;
в)
;
в)
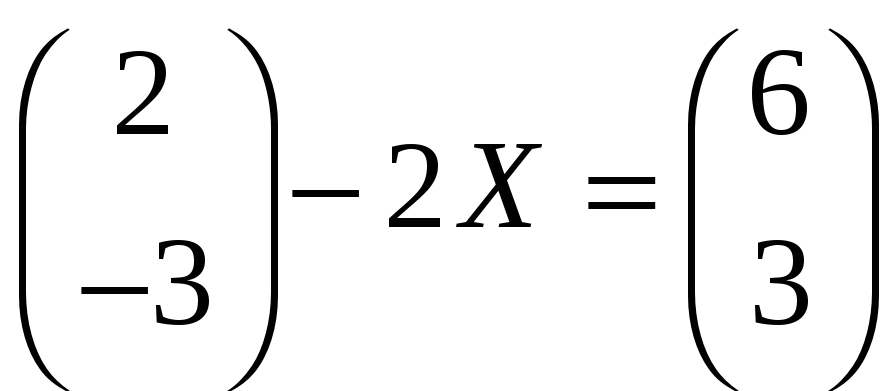 ;
;
г)
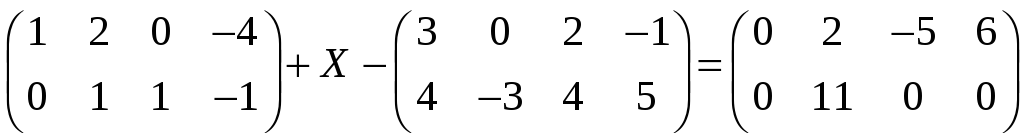 ;
;
д)
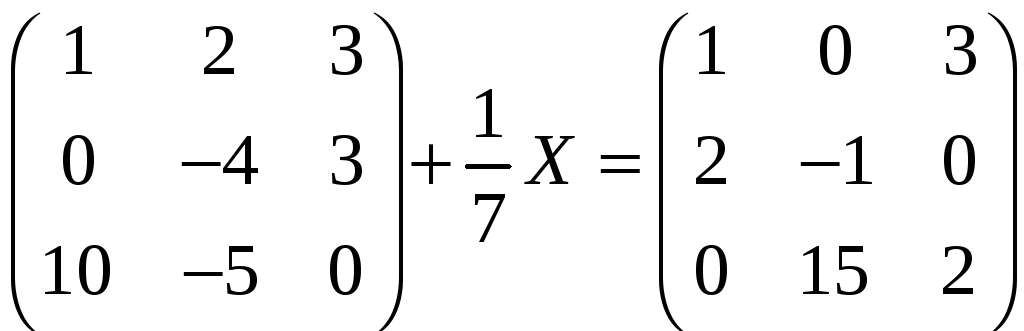 .
.
Задача 3.3. Знайти матриці X та Y, якщо:
а)
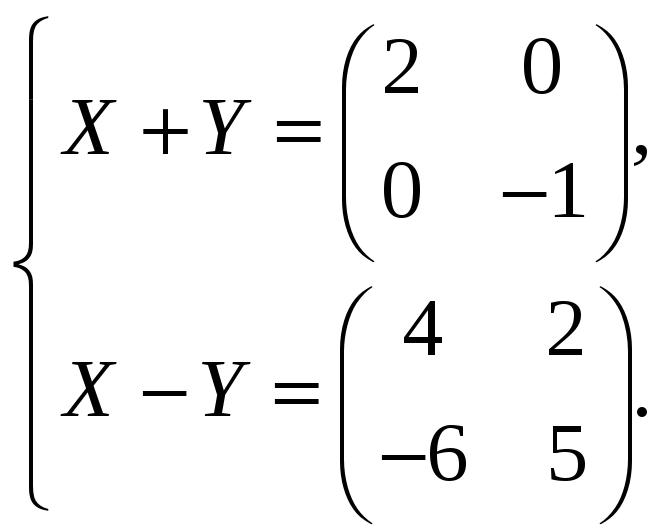 б)
б)
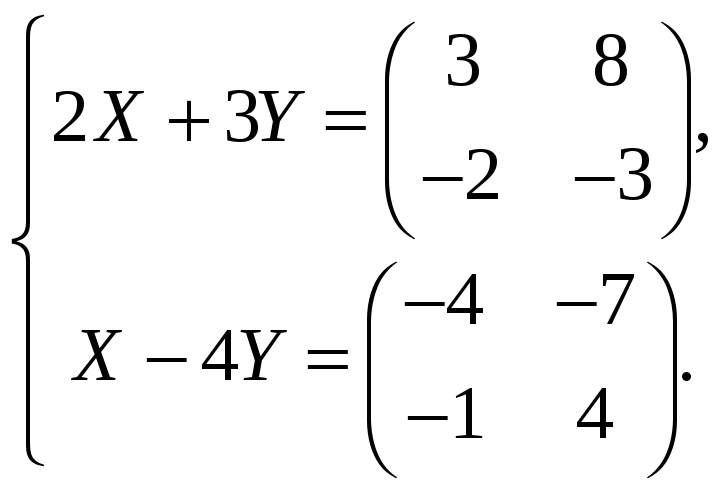
2. Множення матриць
Розглянемо
операцію множення
матриць спочатку для квадратних матриць.
Нехай
![]() і
і
![]() –
квадратні матриці
порядку
n.
–
квадратні матриці
порядку
n.
Добутком
АВ
цих матриць, тобто результатом виконання
операції множення
матриць A
і
B
будемо називати матрицю
![]() ,
елементи
якої визначаються за правилом:
,
елементи
якої визначаються за правилом:
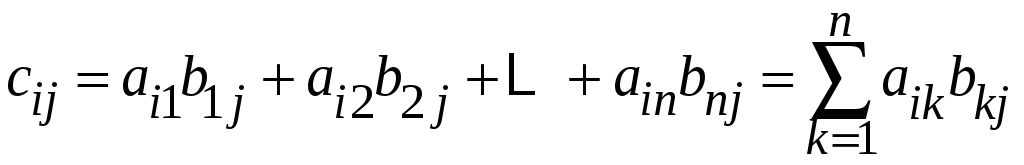 (1
i,
j
n).
(1
i,
j
n).
Отже,
добутком
АВ
квадратних матриць A
і B
n-го
порядку є квадратна матриця того ж
порядку n,
причому коли
![]() ,
то будь-який елемент
,
то будь-який елемент
![]() дорівнює сумі попарних добутків
відповідних елементів i-го
рядка матриці A
та
дорівнює сумі попарних добутків
відповідних елементів i-го
рядка матриці A
та
j-го стовпця матриці B.
Приклад
3.4.
Нехай A
=
 ;
B
=
;
B
=
 .
Знайдемо добутки AB
і BA.
.
Знайдемо добутки AB
і BA.
AB
=
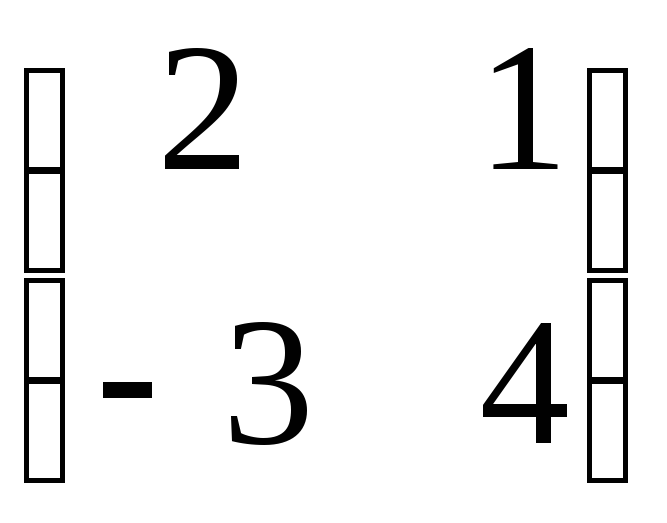
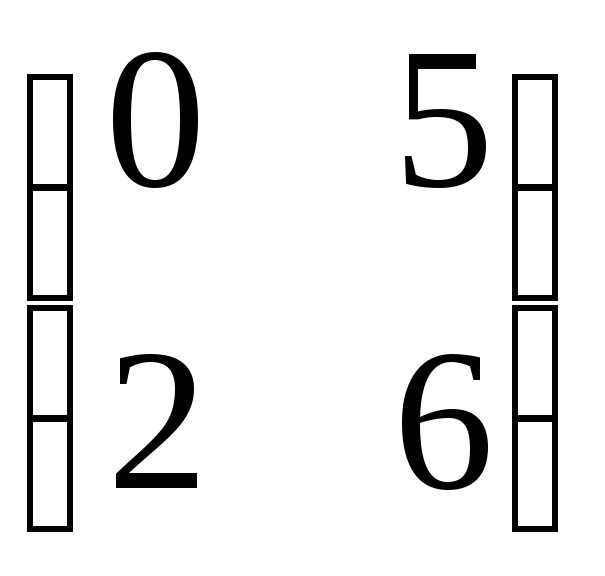 =
=
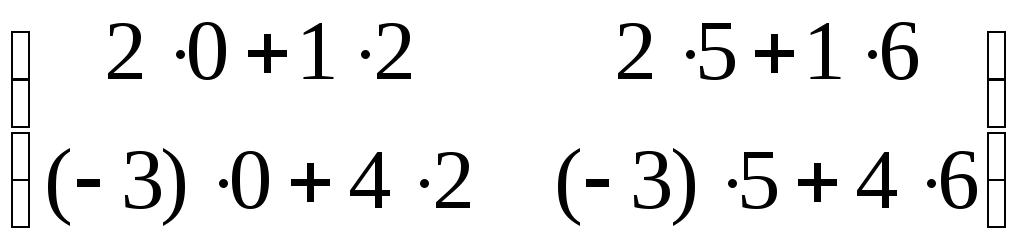 =
=
 ;
;
BA
=
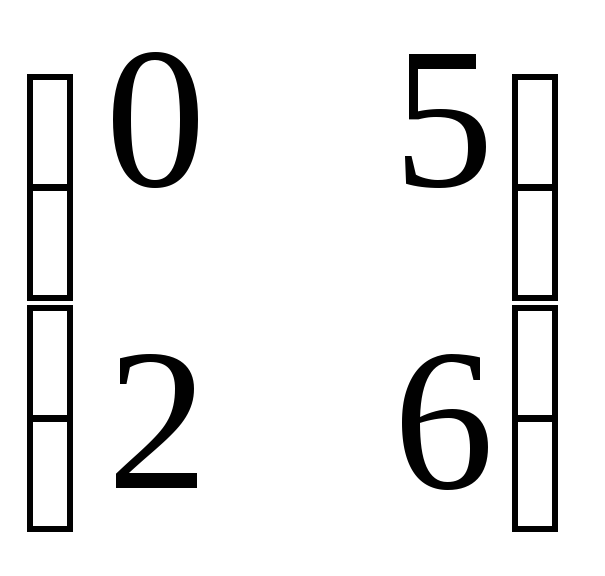
 =
=
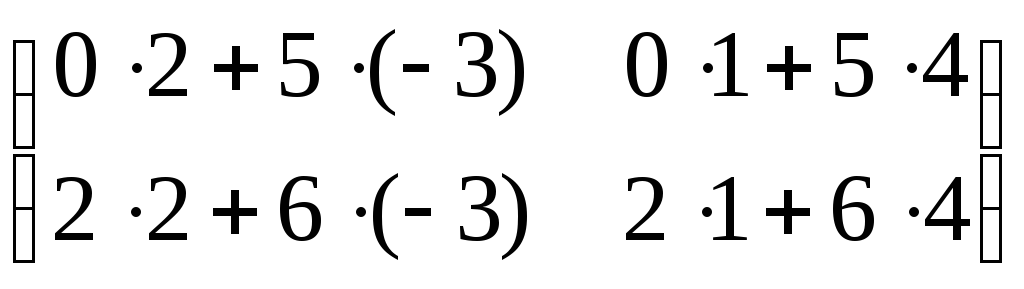 =
=
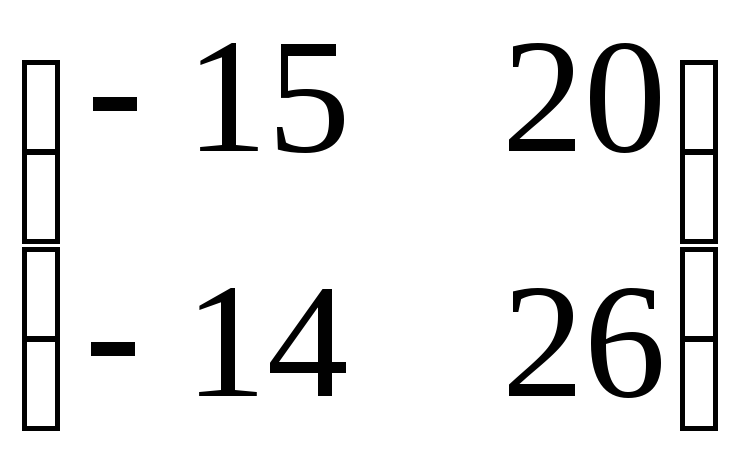 .
.
З цього прикладу видно, що множення матриць некомутативне, тобто в загальному випадку
AB BA.
Квадратні матриці А і В, для яких АВ = ВА, називаються комутуючими, або переставними. Прикладом переставних матриць є діагональні матриці однакових порядків.
Для
будь-яких квадратних матриць A,
B,
С
порядку
n
і будь-якого дійсного числа
![]() є вірними рівності:
є вірними рівності:
1. (АВ)С = А(ВС) (асоціативність множення);
2. (А + В)С = АС + ВС;
3. А(В + С) = АВ + АС;
4. (АВ) = (А)В = А(В).
Оскільки множення матриць асоціативне, то можна говорити про однозначно визначений добуток будь-якого скінченного числа матриць n-го порядку, взятих (у зв’язку з некомутативністю множення) у певному порядку.
Діагональна матриця порядку n, всі елементи головної діагоналі якої дорівнюють числу 1, називається одиничною матрицею n-го порядку позначається символом E. Таким чином
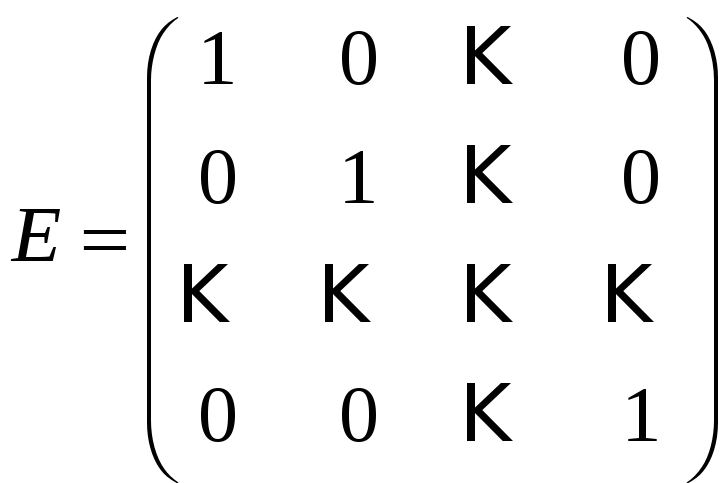 .
.
Якщо E – одинична матриця порядку n, то
АЕ = ЕА = А
для кожної квадратної матриці A n-го порядку.
Нехай A – квадратна матриця n-го порядку. Для будь-якого натурального числа m степінь матриці A визначається так:
![]() .
.
Під степенем ненульової матриці A з нульовим показником розуміють одиничну матрицю E того ж порядку, що і A, тобто
![]() .
.
Оскільки операція множення матриць асоціативна, то для будь-якої квадратної матриці A та будь-яких цілих невід’ємних чисел m, n мають місце рівності:
1.
![]() ,
,
2.
![]() .
.
Теорема. Визначник добутку квадратних матриць A і B однакових порядків дорівнює добутку визначників цих матриць, тобто
det(AB) = detA·detB.
Доведення див., напр., в [3].
Приклад
3.5.
Нехай
A
=
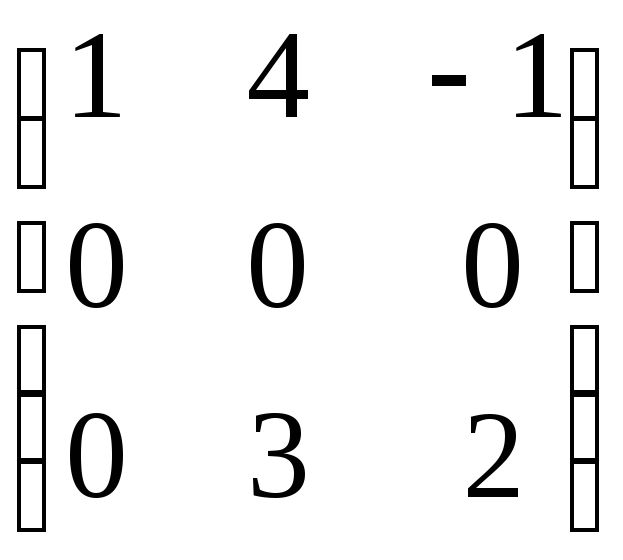 ,
B
=
,
B
=
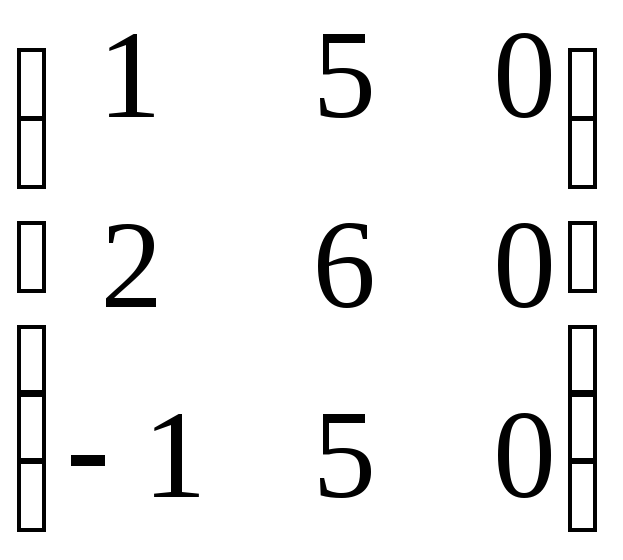 .
Знайдемо матрицю
.
Знайдемо матрицю
![]() .
.
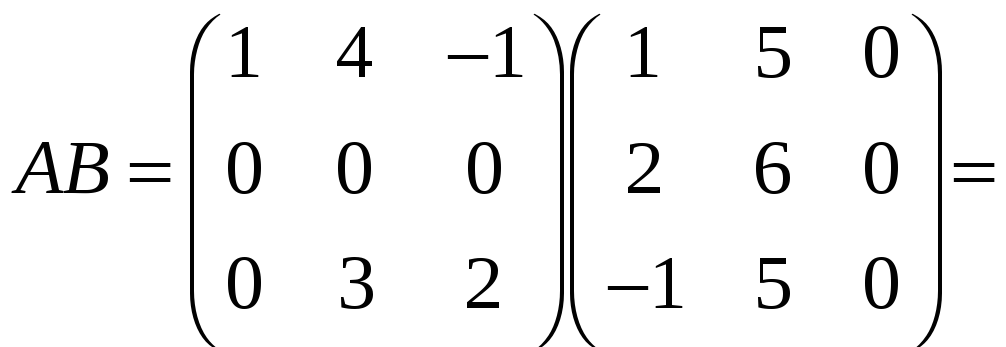
=
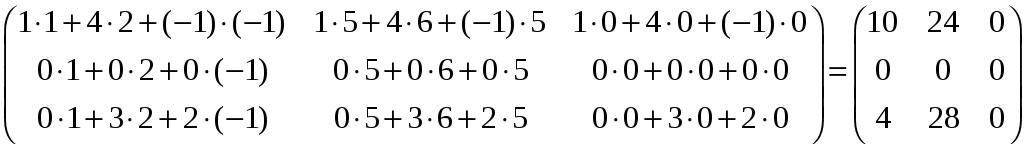 .
.
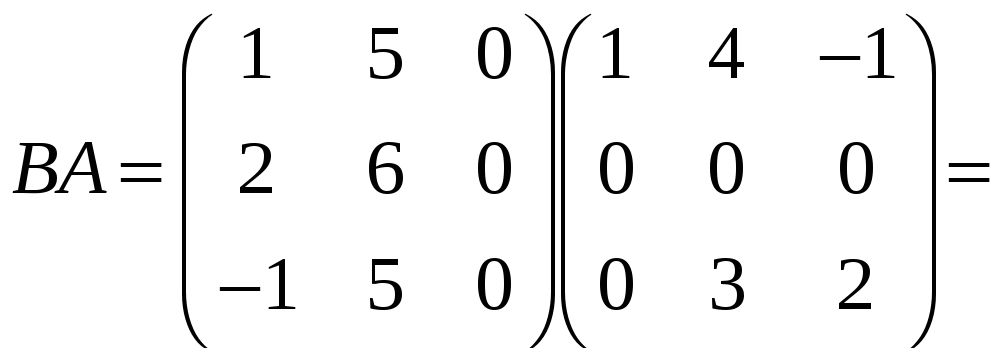
=
 .
.
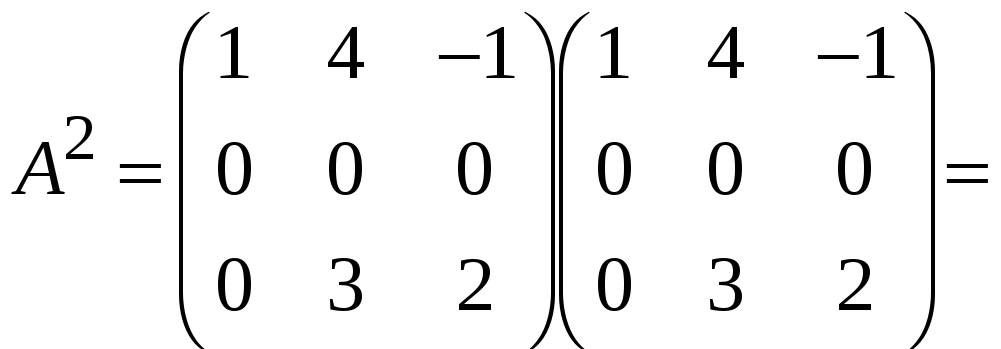
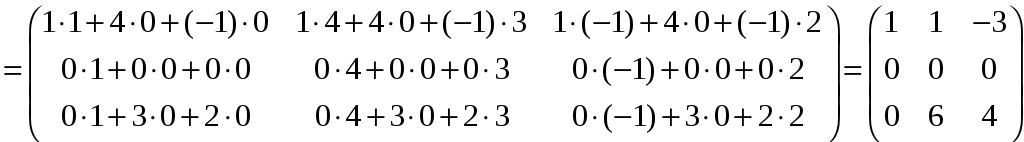 .
.
 =
=
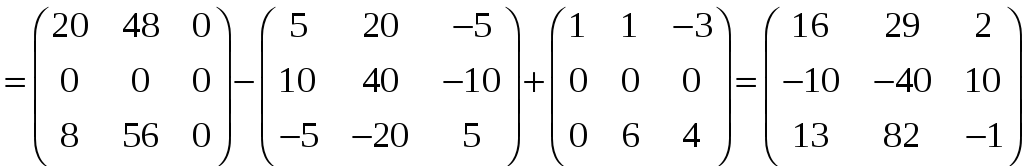 .
.
Приклад
3.6.
Знайдемо всі матриці, переставні з
матрицею
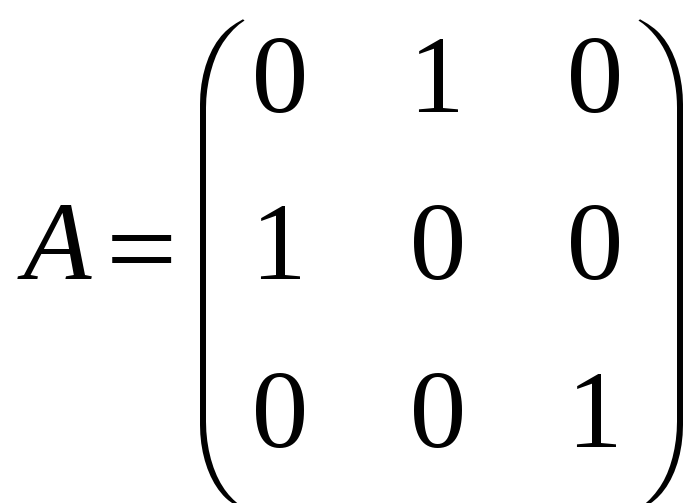 .
.
Матриця,
переставна з A
є
квадратною порядку 3. Нехай
 і
і
AB = BA. Тоді
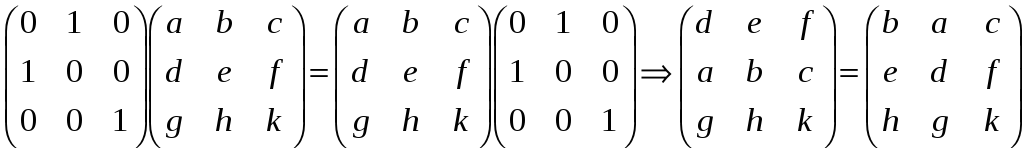 .
.
Матриці однакового порядку рівні, якщо рівні їх відповідні коефіцієнти. Отже,
a = e, b = d, c = f, g = h,
а,
значить, будь-яка матриця, переставна
з A,
має вигляд
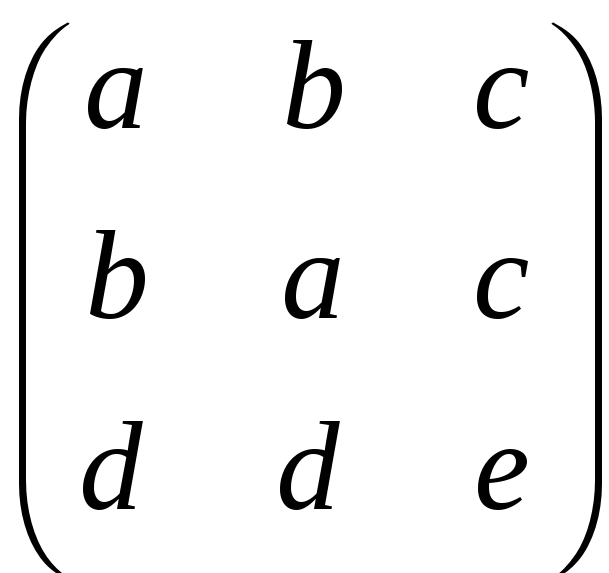 .
.
Приклад
3.7.
Нехай
 .
Знайдемо
.
Знайдемо
![]() (m
N).
(m
N).
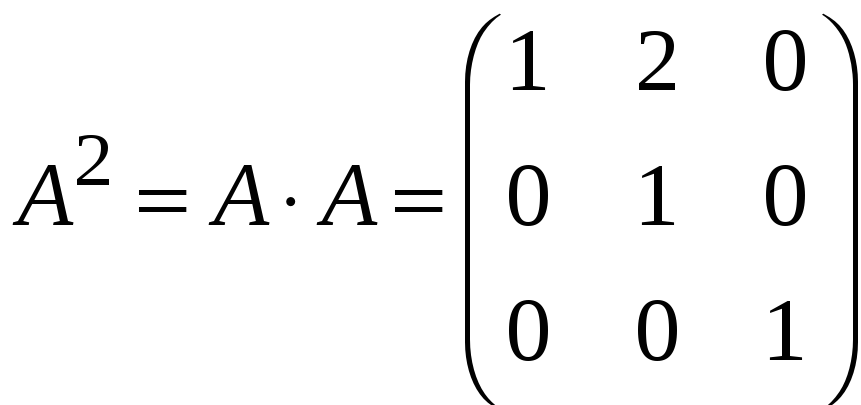 ,
,
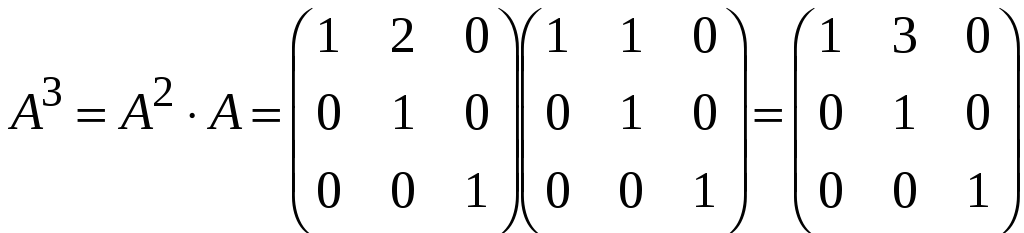 .
.
Застосуємо метод математичної індукції. Припустимо, що
 .
.
Тоді
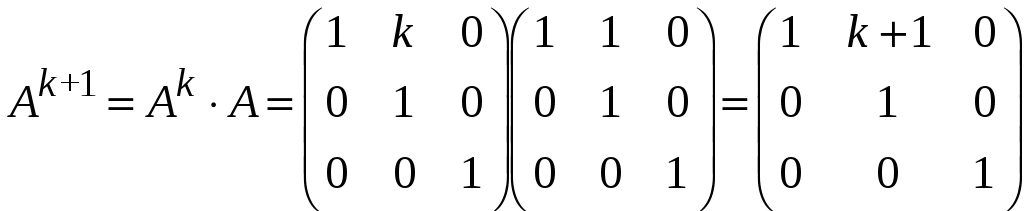 .
.
Наше припущення правильне. Отже, для будь-якого m N:
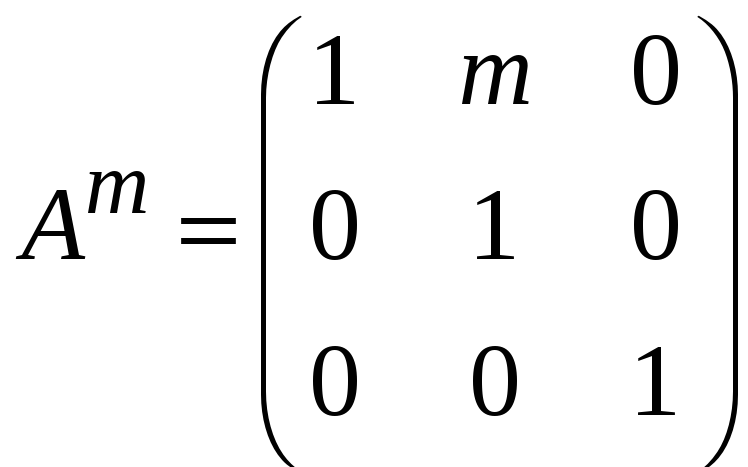 .
.
Нехай
![]() – деякий многочлен від змінної x
з дійсними коефіцієнтами і A
– квадратна матриця порядку
n
з
дійсними коефіцієнтами. Під многочленом
– деякий многочлен від змінної x
з дійсними коефіцієнтами і A
– квадратна матриця порядку
n
з
дійсними коефіцієнтами. Під многочленом
![]() від матриці A
розуміють матрицю
від матриці A
розуміють матрицю
![]() ,
,
де E – одинична матриця того ж порядку, що і A.
Приклад
3.8.
Знайдемо
значення
![]() ,
де
,
де
![]() ,
,
 .
.
Маємо:
![]() ,
де E
– одинична матриця порядку 3.
,
де E
– одинична матриця порядку 3.
Оскільки
![]() ,
то
,
то
![]() для будь-якого n
N,
а, значить,
для будь-якого n
N,
а, значить,
![]() .
.
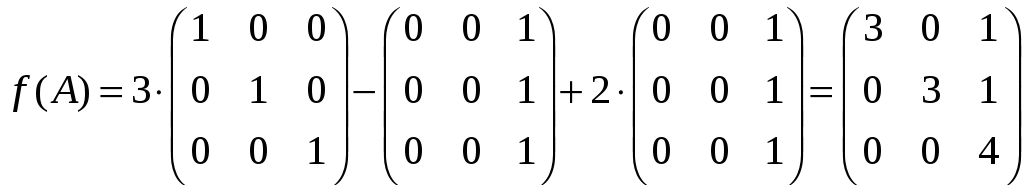 .
.
Задача 3.4. Знайти добутки AB і BA, якщо:
а)
 ,
,
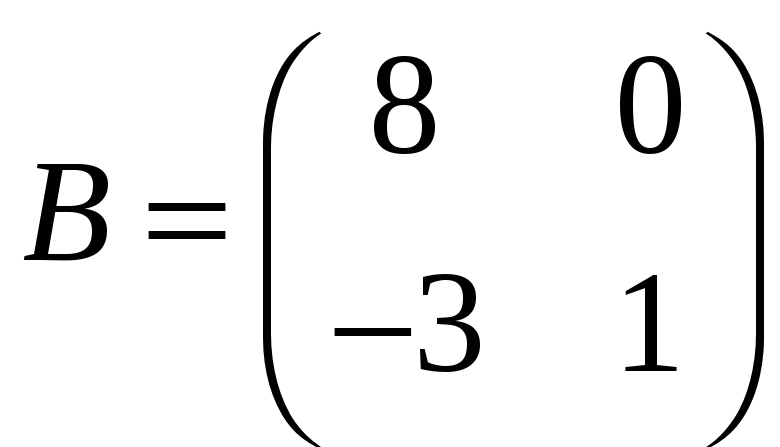 ;
б)
;
б)
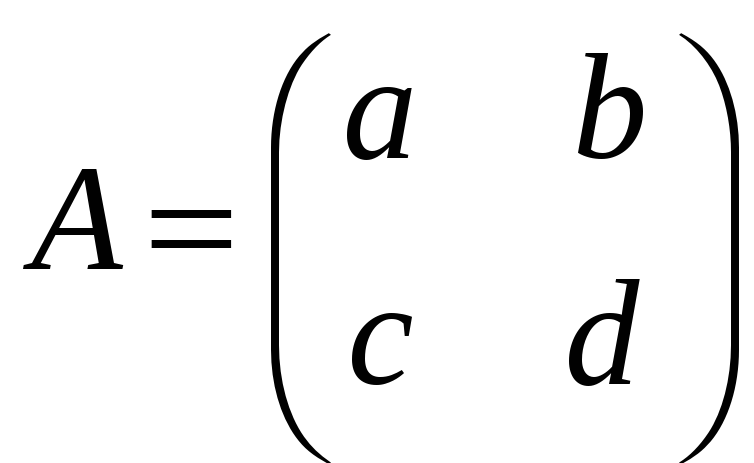 ,
,
 ;
;
в)
 ,
,
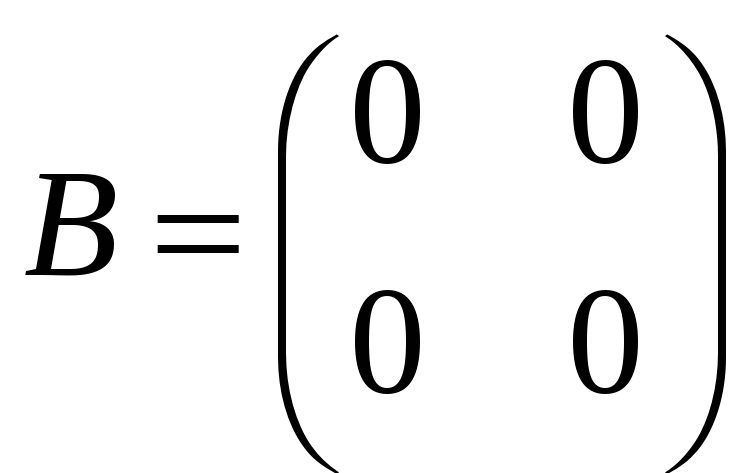 ;
г)
;
г)
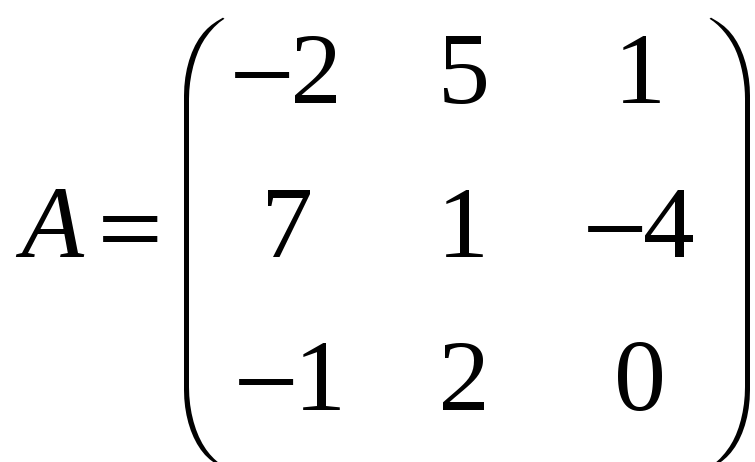 ,
,
 ;
;
д)
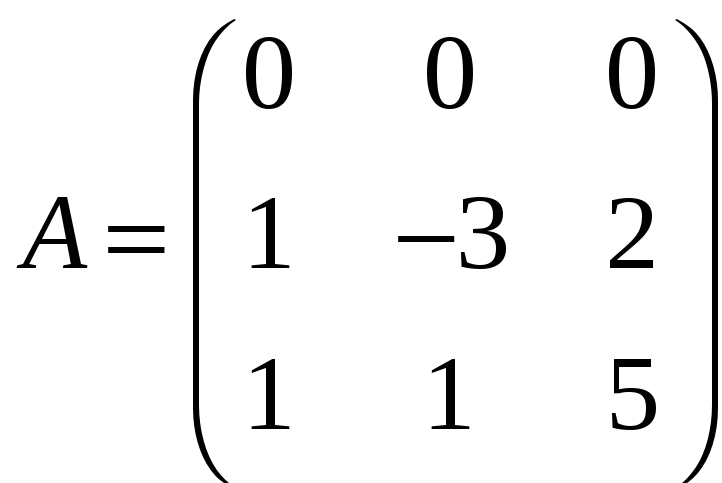 ,
,
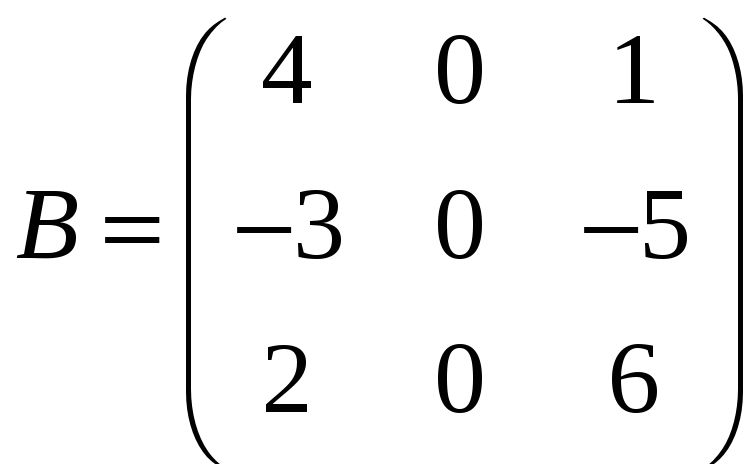 ;
е)
;
е)
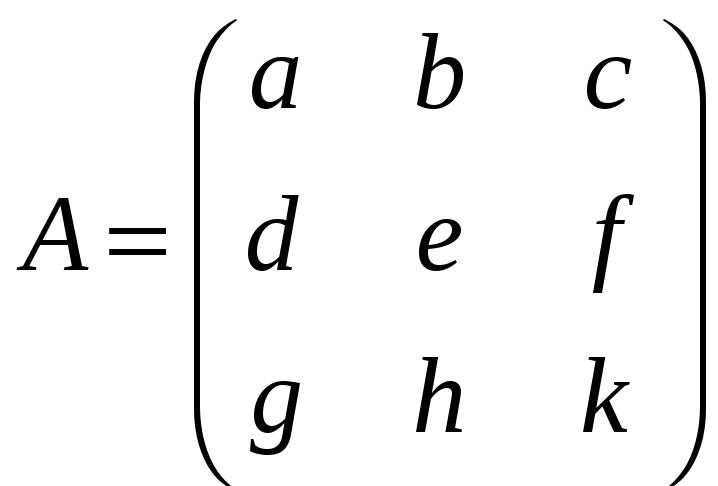 ,
,
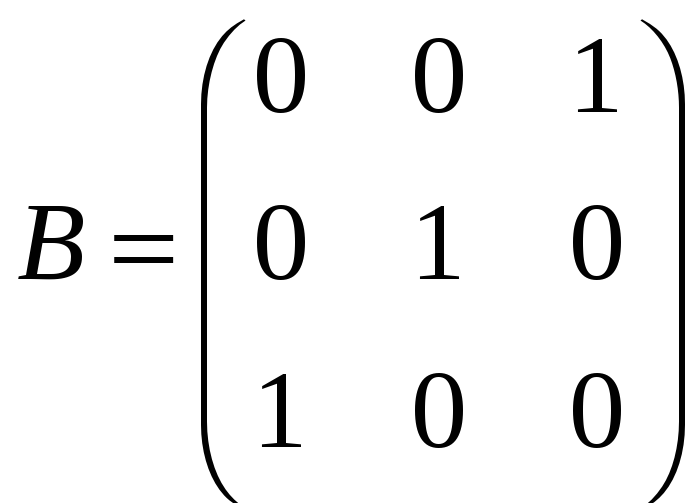 ;
;
є)
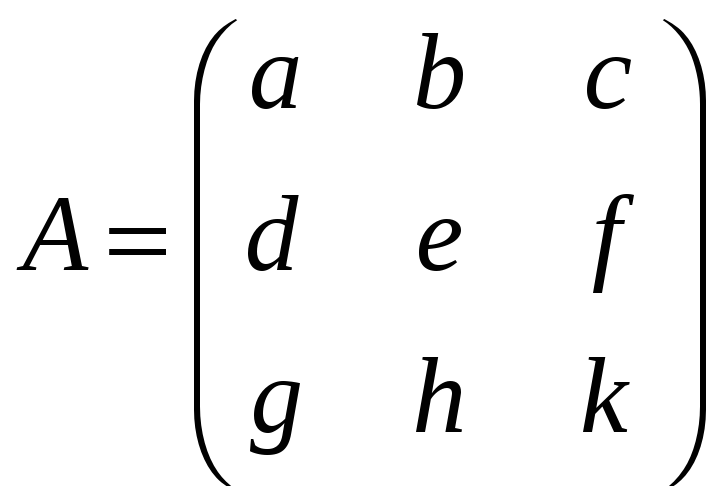 ,
,
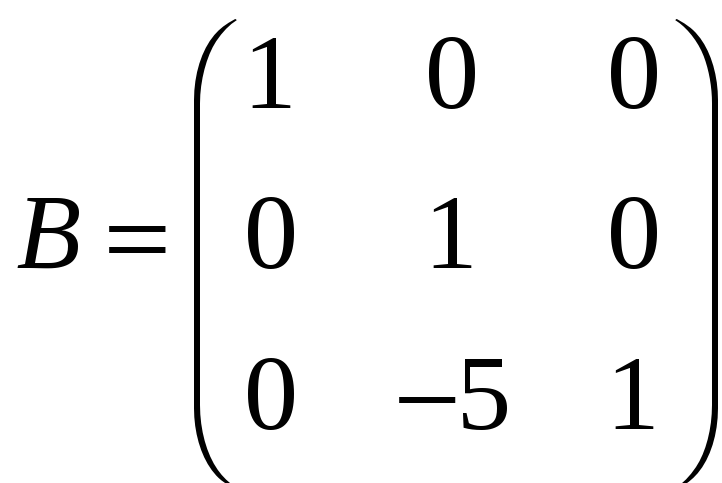 ;
ж)
;
ж)
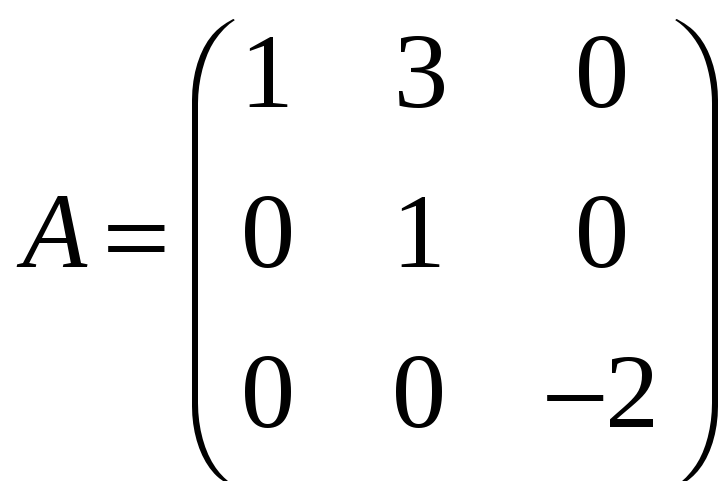 ,
,
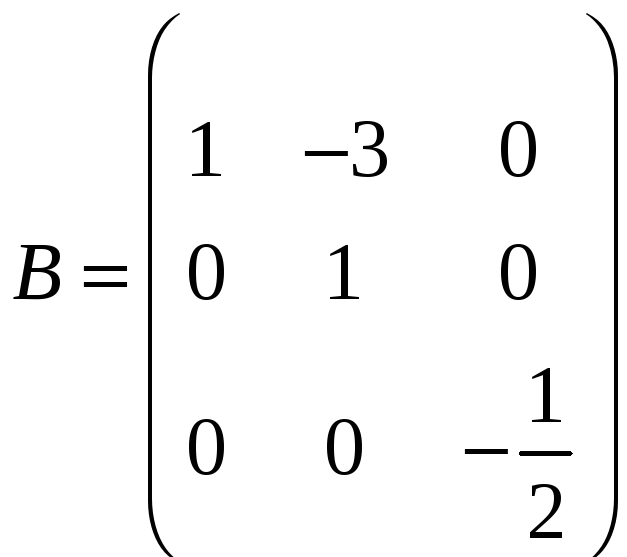 ;
;
з)
 ,
,
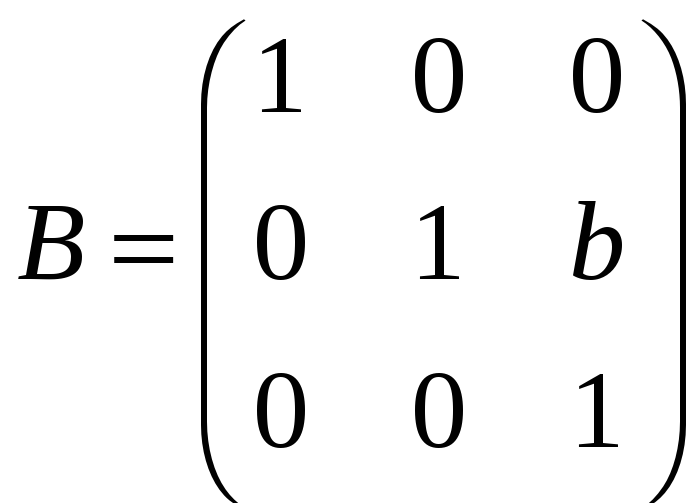 ;
і)
;
і)
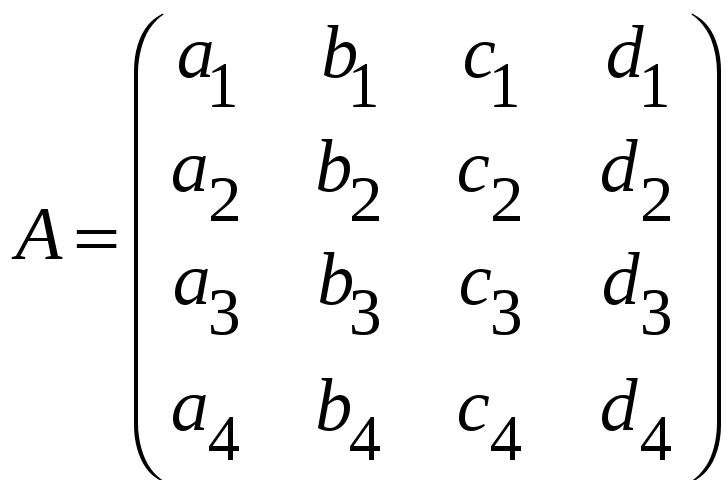 ,
,
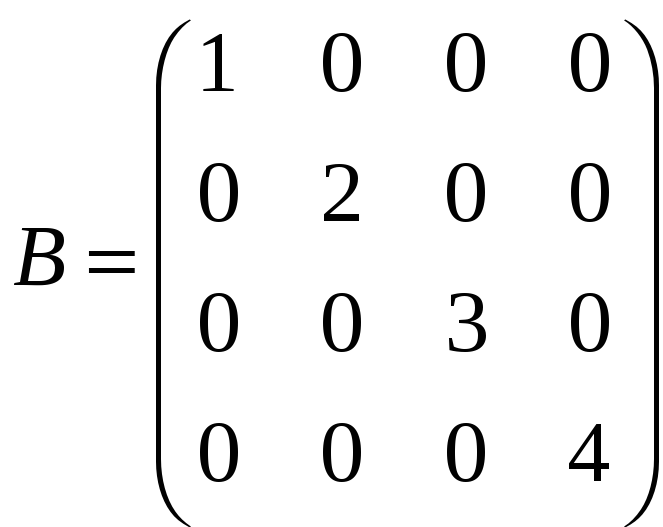 ;
к)
;
к)
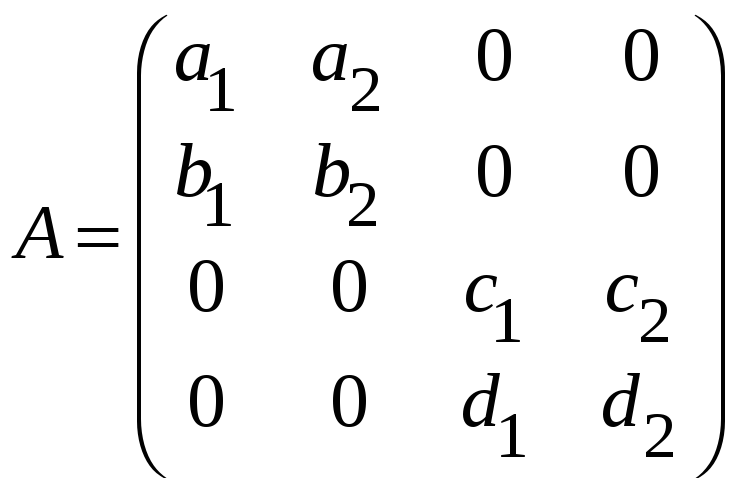 ,
,
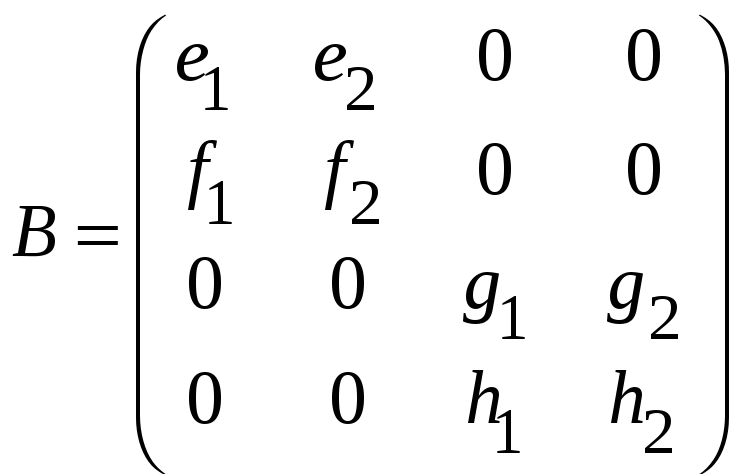 .
.
Задача
3.5.
Знайти
матрицю
![]() ,
якщо A
=
,
якщо A
=
 ,
,
B
=
 .
.
Задача
3.6.
Знайти
![]() (m
N),
якщо:
(m
N),
якщо:
а)
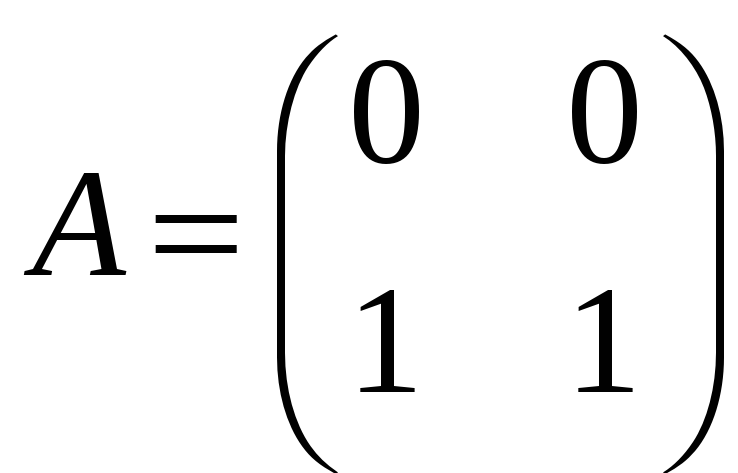 ;
б)
;
б)
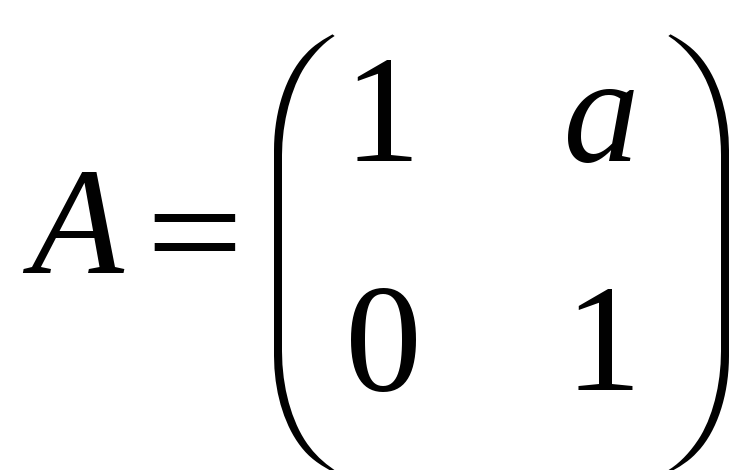 ;
в)
;
в)
 ;
г)
;
г)
 ;
;
д)
 ;
е)
;
е)
 ;
є)
A =
;
є)
A =
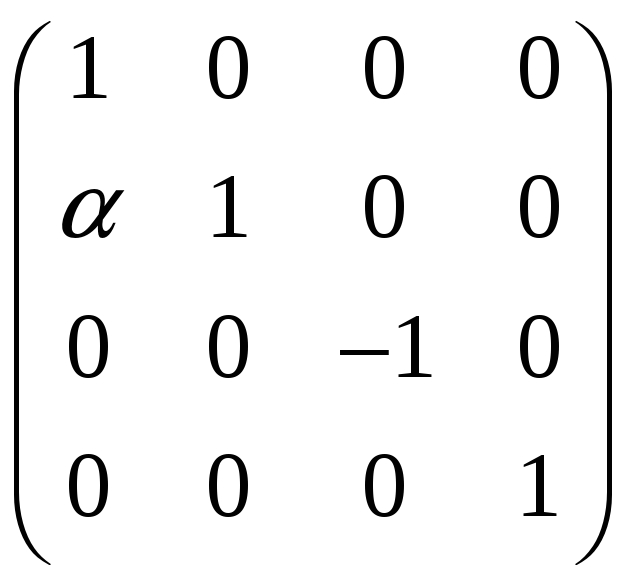 ;
;
ж)
A =
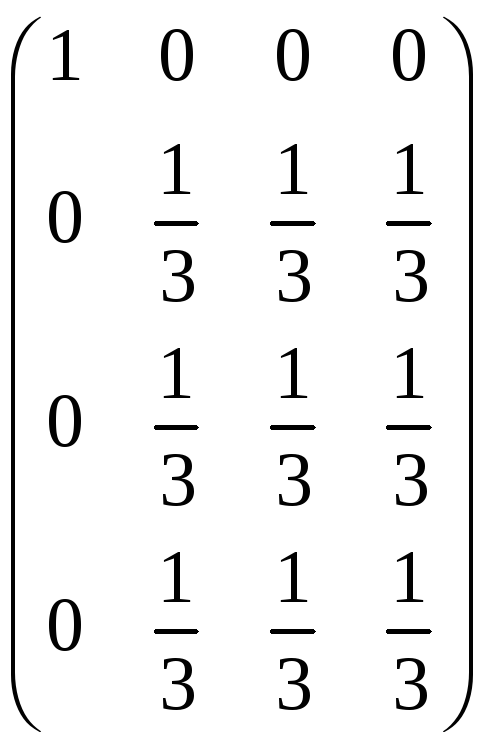 ;
з)
;
з)
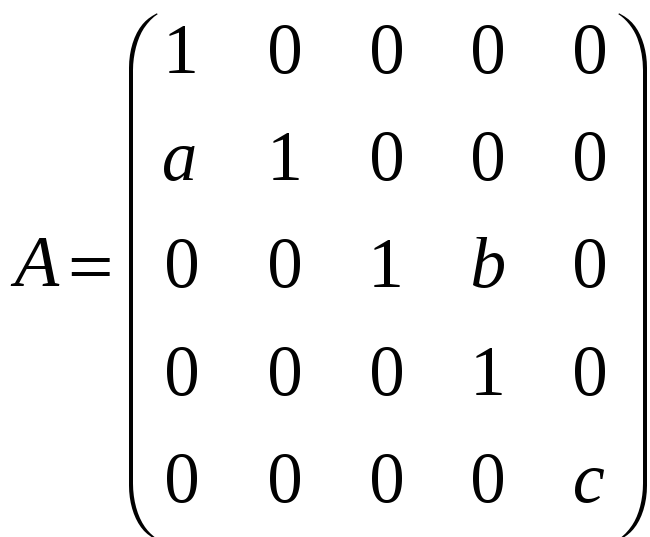 .
.
Задача 3.7. A і B квадратні матриці порядку n. Знайти добутки AB і BA.
а)
 ,
B
= diag(1,
2,
,
n);
,
B
= diag(1,
2,
,
n);
б) A = diag( a1, a2, , an ), B =diag( b1, b2, , bn ).
Задача
3.8.
Знайти
![]() ,
якщо:
,
якщо:
а)
A
=
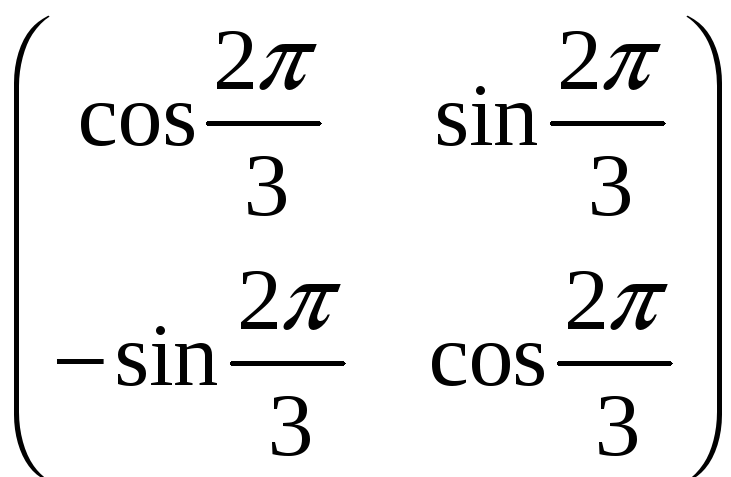 ;
б)
A
=
;
б)
A
=
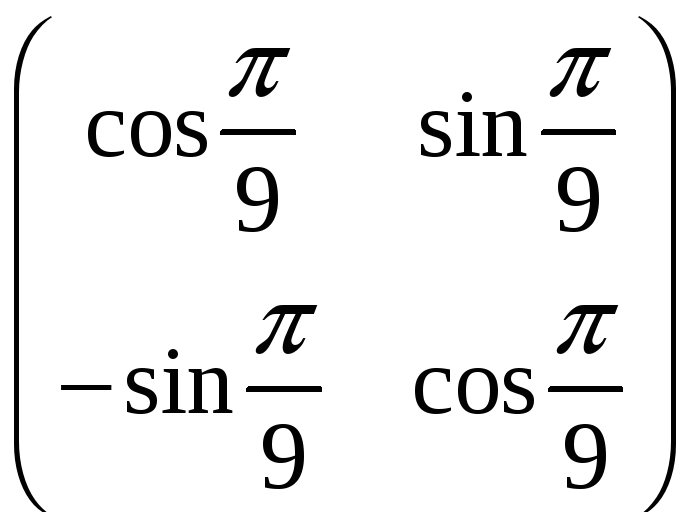 .
.
Задача
3.9.
Знайти
найменше натуральне число k,
таке що![]() .
.
а)
A
=
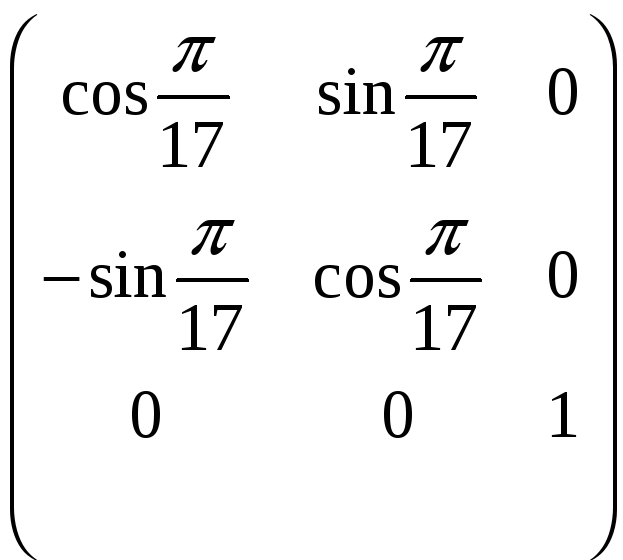 ;
б)
A
=
;
б)
A
=
 ;
;
в)
A
=
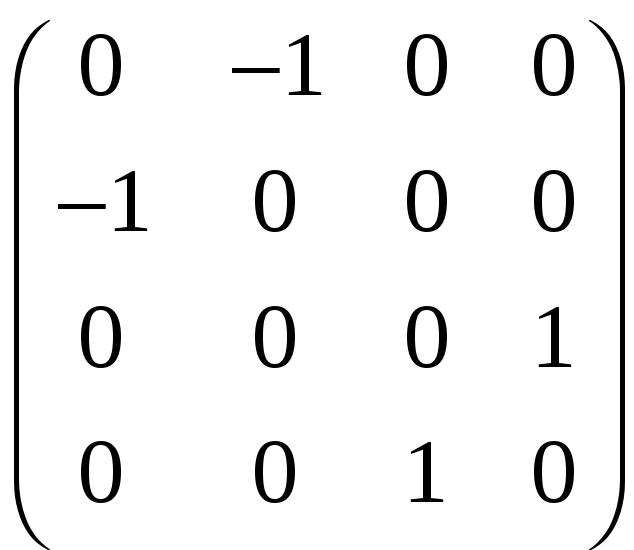 ;
г)
A =
;
г)
A =
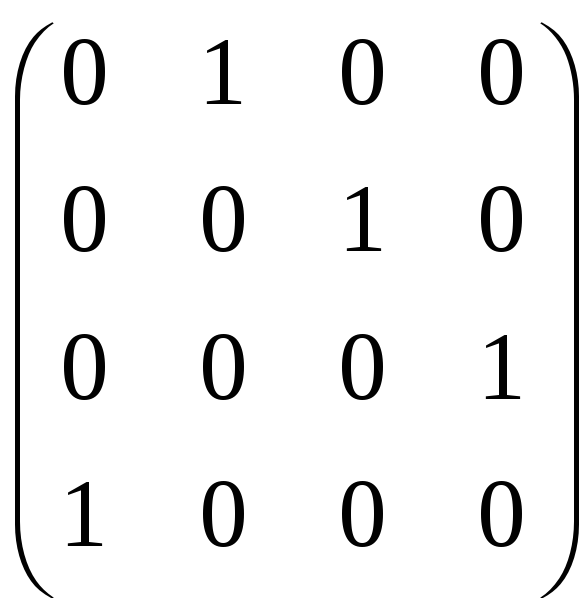 .
.
Задача
3.10.
Навести приклад неодиничної квадратної
матриці A
порядку
2, такої, що
![]() .
.
Задача
3.11.
Довести,
що для будь-яких
натуральних
чисел
n
і
m
існує
неодинична
квадратна матриця A
n-го
порядку, така, що
![]() .
.
Задача
3.12.
Знайти
значення многочлена
![]() від
матриці A.
від
матриці A.
а)
![]() ,
,
 ;
б)
;
б)
![]() ,
,
 ;
;
в)
![]() ,
,
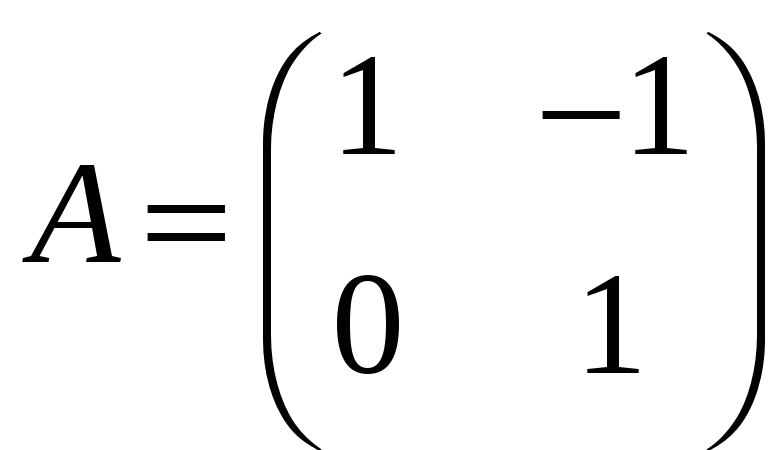 ;
;
г)
![]() ,
,
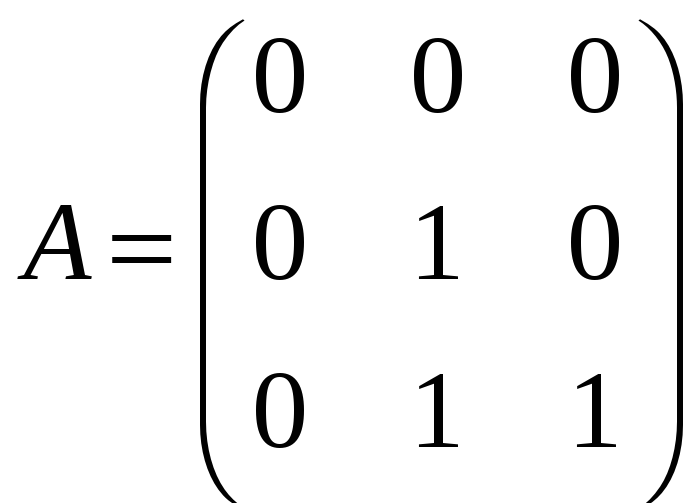 .
.
Задача 3.13. Навести приклад двох ненульових квадратних матриць A і B, таких, що добуток AB дорівнює нульовій матриці.
Задача
3.14.
Навести приклад ненульової квадратної
матриці A,
такої, що
![]() дорівнює нульовій матриці при будь-якому
натуральному m
2.
дорівнює нульовій матриці при будь-якому
натуральному m
2.
Задача 3.15. Знайти множину всіх квадратних матриць, переставних з матрицею A.
а)
 ;
б)
;
б)
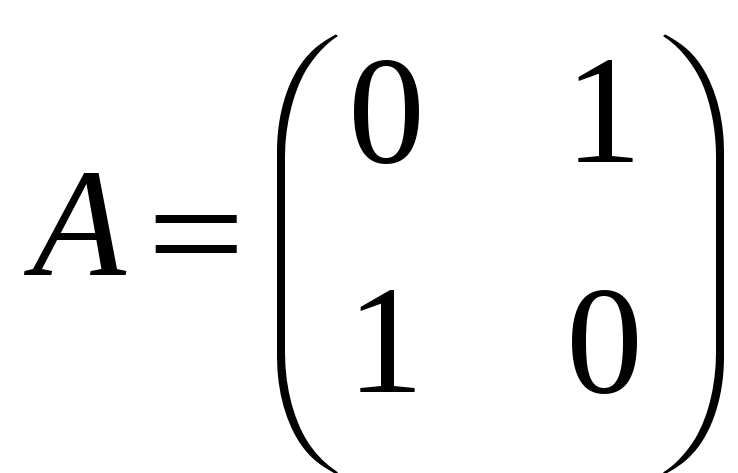 ;
в)
;
в)
 ;
г)
;
г)
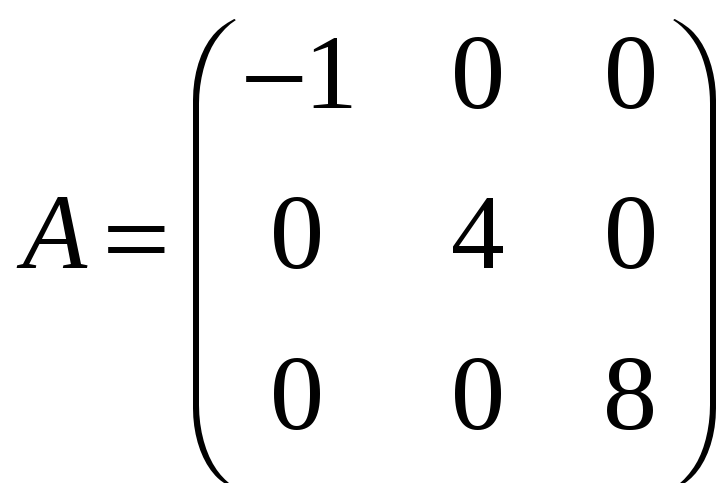 ;
;
д)
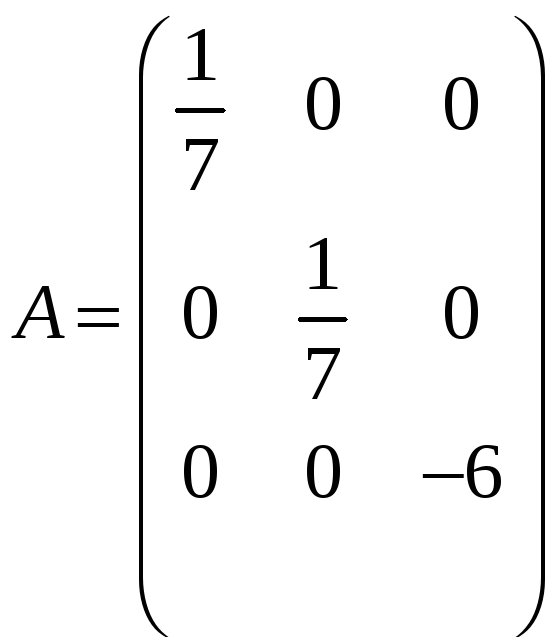 ;
е)
;
е)
 .
.
Задача 3.16. Нехай A – діагональна матриця порядку n, всі елементи головної діагоналі якої різні. Довести, що матриця B n-го порядку переставна з A тоді і тільки тоді, коли B є діагональною.
Задача 3.17. Нехай A – скалярна матриця n-го порядку. Знайти всі квадратні матриці, переставні з A.
Задача
3.18.
Нехай A
– квадратна матриця порядку 2, така, що
trA
=
0.
Довести,
що матриця
![]() є скалярною.
є скалярною.
Задача
3.19.
Елементи матриці
![]() визначені за правилом:
визначені за правилом:
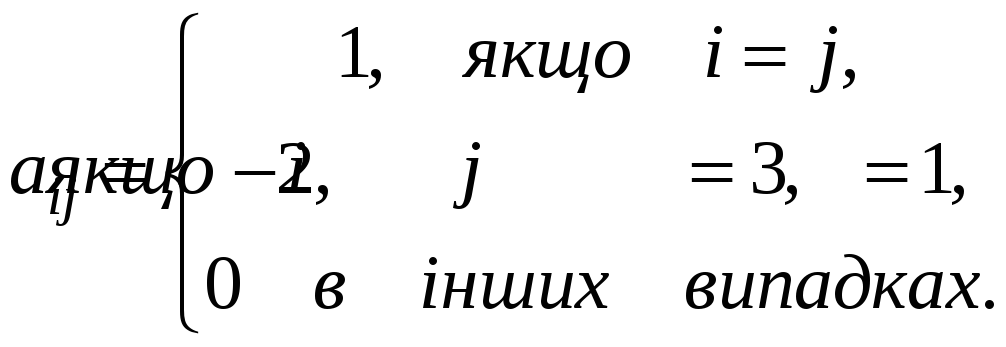
Знайти
елементи матриці B,
якщо
![]() .
.
Задача
3.20.
Елементи матриць
![]() і
і
![]() (n
2) визначені
за правилами
(n
2) визначені
за правилами

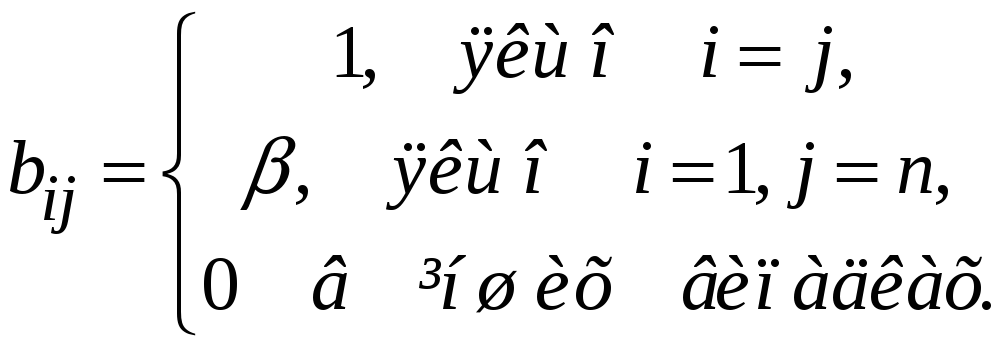
(![]() і
і
![]()
деякі дійсні числа).
Знайти
елементи матриць С
і
D,
якщо С
= AB,
деякі дійсні числа).
Знайти
елементи матриць С
і
D,
якщо С
= AB,
D = BA.
Задача
3.21.
Нехай
 .
Елементи матриці
.
Елементи матриці
![]() визначені за правилом
визначені за правилом
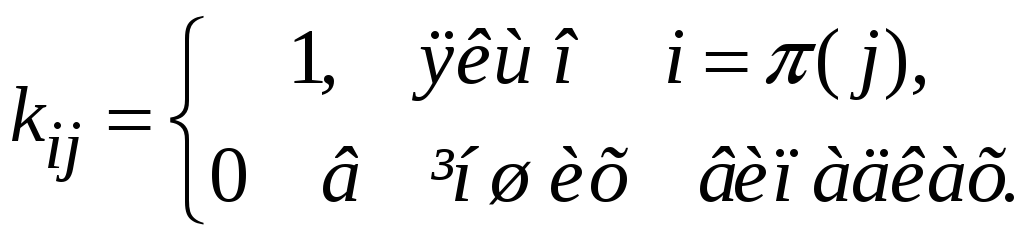
Знайти
найменше натуральне число m
таке,
що
![]() .
.
Задача 3.22. Як зміниться квадратна матриця A n-го порядку, якщо її помножити на матрицю В = diag ( b1, b2, , bn ): а) зліва; б) справа?
Задача 3.23. Як зміниться квадратна матриця A n-го порядку, якщо її помножити на матрицю
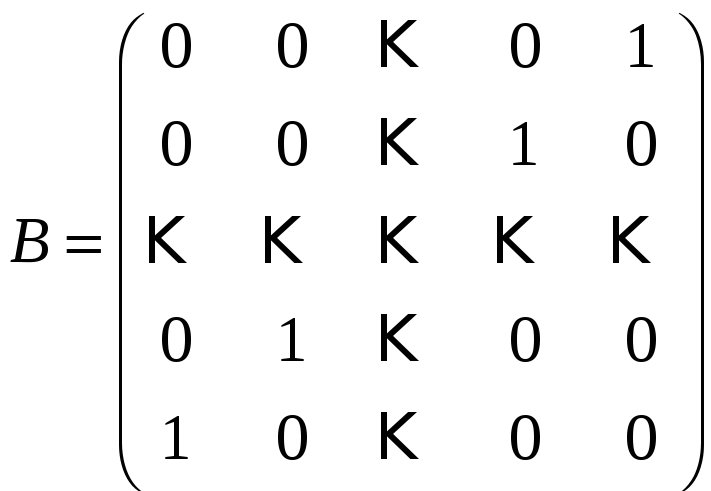 порядку
n:
порядку
n:
а) зліва; б) справа?
Задача
3.24. Нехай
![]() – деяка підстановка n-го
степеня. Елементи
матриці
– деяка підстановка n-го
степеня. Елементи
матриці
![]() визначені за правилами:
визначені за правилами:
 .
.
Довести,
що
![]() тоді і тільки тоді, коли
тоді і тільки тоді, коли
![]() .
.
Задача 3.25. Нехай A, B, C – квадратні матриці однакових порядків, detA = 2, detB = 3, detC = –1. Знайти det(ABCAt).
Задача
3.26.
Нехай
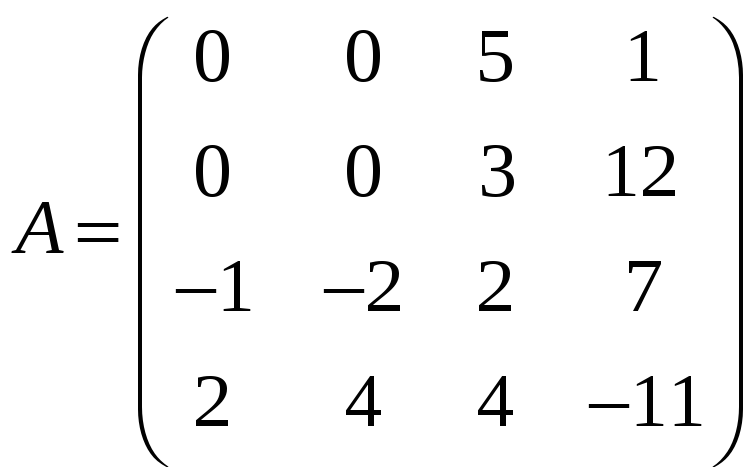 ,
B1,
B2,
,
Bn
– квадратні матриці четвертого порядку.
Знайти:
,
B1,
B2,
,
Bn
– квадратні матриці четвертого порядку.
Знайти:
а) detC, якщо С = AB1 + AB2 + ··· + ABn;
б) detD, якщо D = B1At + B2At + ··· + BnAt.
Множення матриць поширюється і на прямокутні матриці. При цьому наведене вище означення залишається. Добуток AB двох прямокутних матриць A і B визначений тільки у випадку, коли кількість стовпців матриці A дорівнює кількості рядків матриці B. Матриця-добуток AB має стільки рядків, скільки їх у першому множнику A, а стовпців – стільки, скільки їх має другий множник B, причому, якщо
![]() і
і
![]() і
і
![]() ,
то елементи
,
то елементи
![]() визначаються
за правилом
визначаються
за правилом
 (1
i
k,
1
j
t).
(1
i
k,
1
j
t).
Приклад
3.9.
Нехай
 ,
,
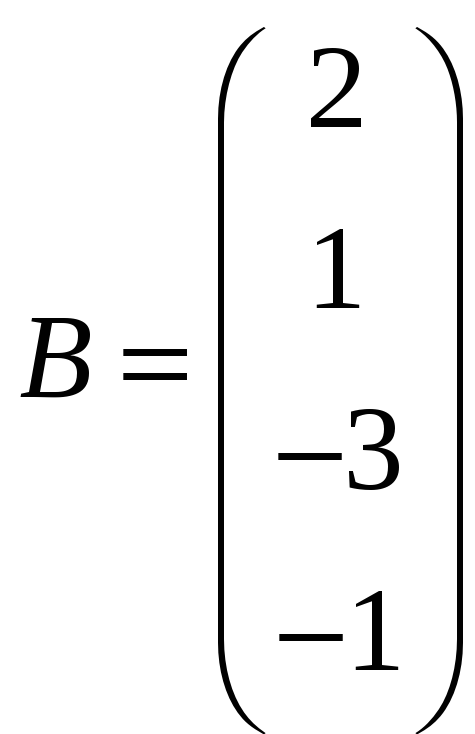 .
З’ясуємо, який з добутків AB
і BA
є визначеним і знайдемо той, що є
визначеним.
.
З’ясуємо, який з добутків AB
і BA
є визначеним і знайдемо той, що є
визначеним.
Число стовпців матриці A дорівнює числу рядків матриці B, а, значить, добуток AB визначений. Кількість рядків у матриці AB дорівнює кількості рядків в A, отже, AB має два рядки. Оскільки матриця B має один стовпець, то і в AB також один стовпець.
 .
.
Число стовпців матриці B і число рядків матриці A різні, отже, добуток BA невизначений.
Приклад
3.10.
Для матриць
![]() і
і
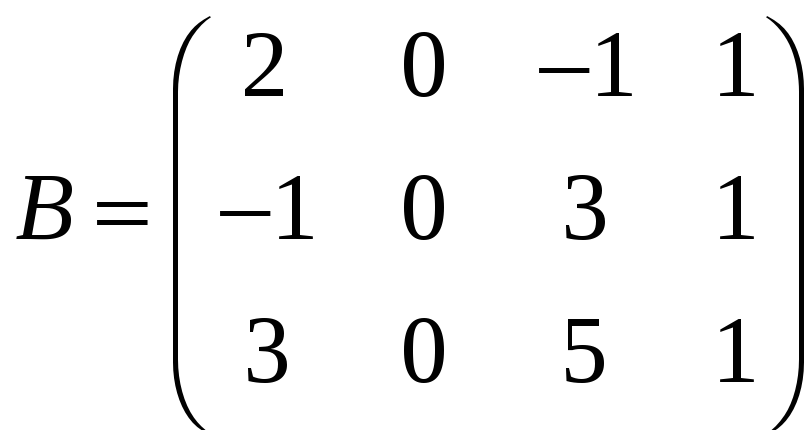 знайдемо той із добутків AB,
BA,
який є визначеним.
знайдемо той із добутків AB,
BA,
який є визначеним.
Добуток AB визначений, оскільки в матриці A три стовпці і стільки ж рядків у матриці B. Матриця AB має один рядок і чотири стовпці.
 =
=
=
=![]() =
=
=
![]() .
.
Добуток BA не є визначеним, оскільки кількість стовпців B не дорівнює числу рядків матриці A.
Задача 3.27. З’ясувати, які з добутків AB, BA є визначеними і знайти ті, що є визначеними.
а)
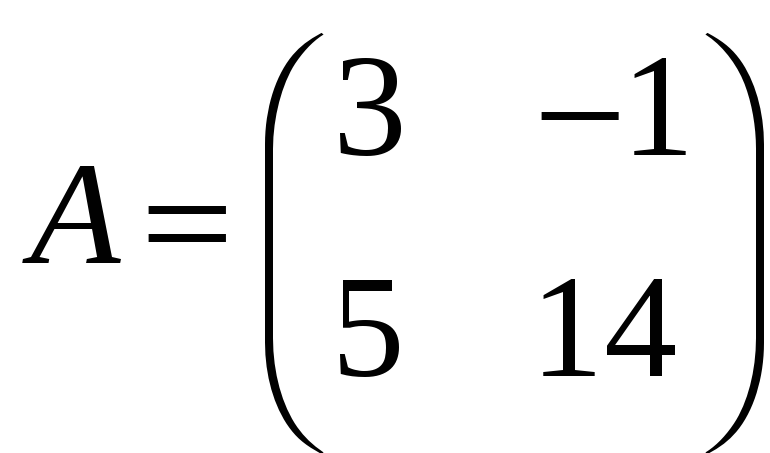 ,
,
 ;
б)
;
б)
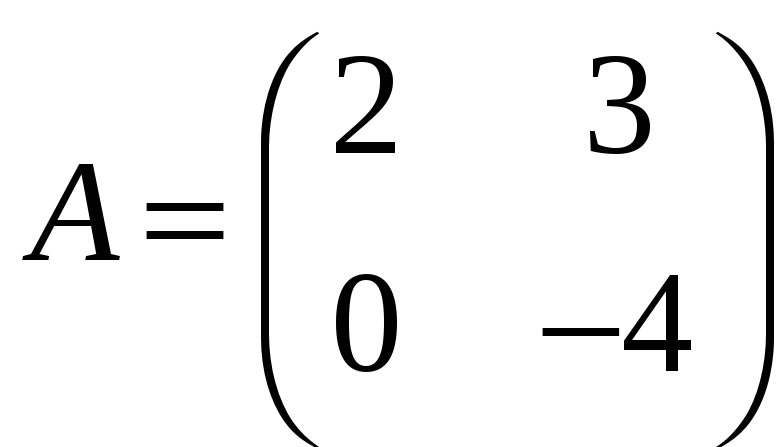 ,
,
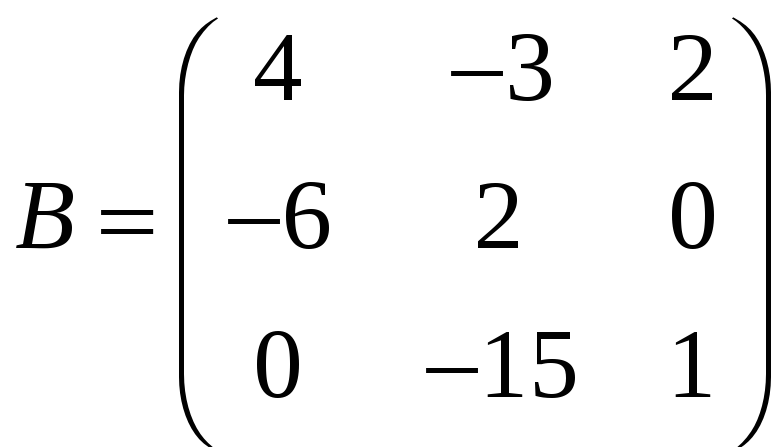 ;
;
в)
 ,
,
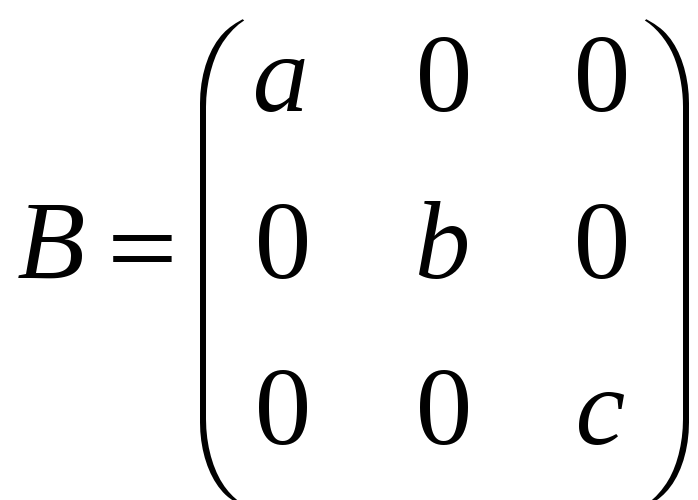 ;
г)
;
г)
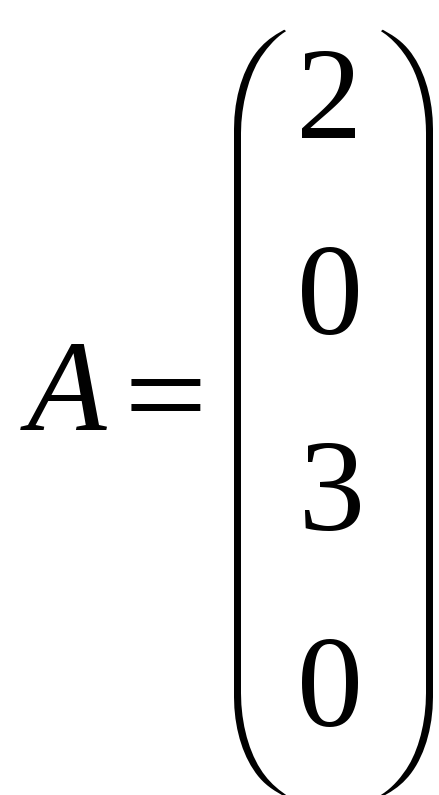 ,
,
![]() ;
;
д)
![]() ,
,
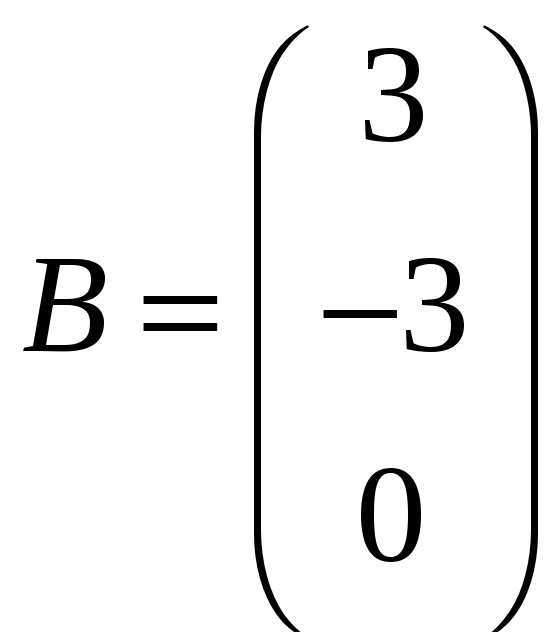 ;
е)
;
е)
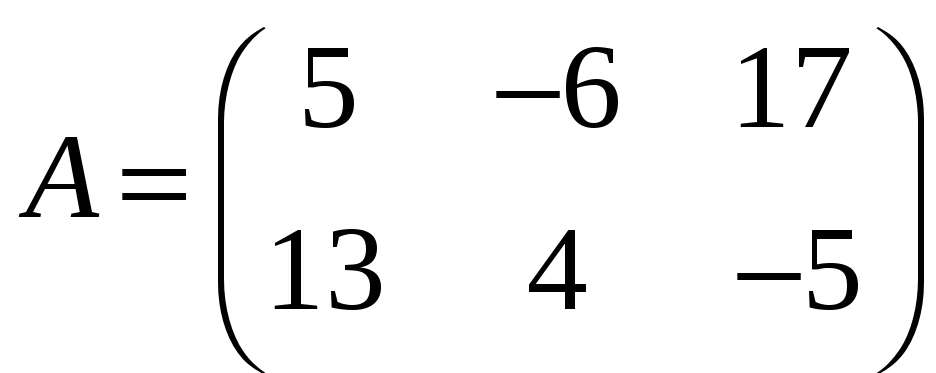 ,
,
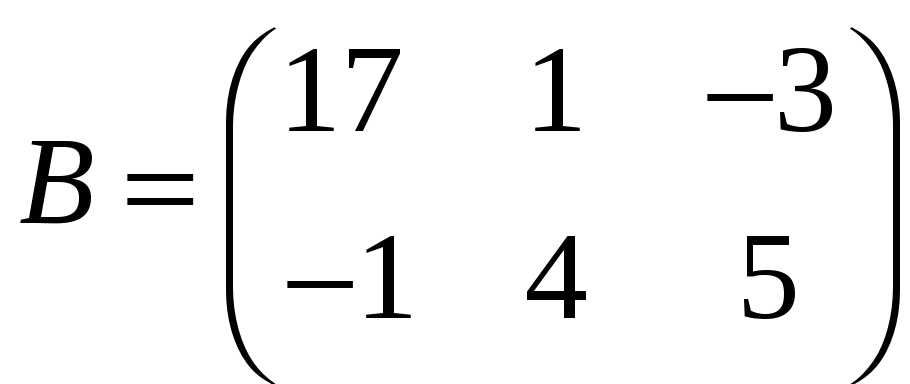 .
.
Задача
3.28.
Матриця
![]() має розмір 1
2, матриця
має розмір 1
2, матриця
![]() – 2
3, матриця
– 2
3, матриця
![]() –
–
3 4, І так далі, і насамкінець, матриця має розмір 100 101. З’ясувати, які з поданих добутків є визначеними. Указати кількості рядків і стовпців для тих добутків, що є визначеними.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() .
.
Задача 3.29. Як зміниться добуток AB матриць A і B, якщо:
а) переставити місцями k-й та m-й рядки матриці A?
б) k-й
рядок матриці A
помножити на число
![]() ?
?
в) до k-го рядка
матриці A додати
m-й рядок,
помножений на число
![]() ?
?
г) переставити місцями k-й та m-й стовпці матриці B?
д) k-й
стовпець матриці B
помножити на число
![]() ?
?
е) до k-го
стовпця матриці B додати m-й
стовпець, помножений на число
![]() ?
?
Задача 3.30. Довести, що коли добуток матриць AB визначений і в матриці A k-й рядок нульовий, то в матриці-добутку AB k-й рядок також нульовий. Чи справджується обернене твердження?
Задача 3.31. Довести, що коли добуток матриць AB визначений і в матриці B k-й стовпець нульовий, то в добутку AB k-й стовпець також нульовий. Чи справджується обернене твердження?
3. Транспонування матриці
В
главі 2 розглядалась операція над
матрицями, яка не є арифметичною. Нехай
![]() .
Нагадаємо, що матрицею, транспонованою
до
матриці
А,
називається матриця
.
Нагадаємо, що матрицею, транспонованою
до
матриці
А,
називається матриця
![]() ,
де
,
де
![]() .
.
Операція транспонування має такі властивості:
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
Задача 3.32. Знайти матрицю, транспоновану до матриці A.
а)
![]() ;
б)
;
б)
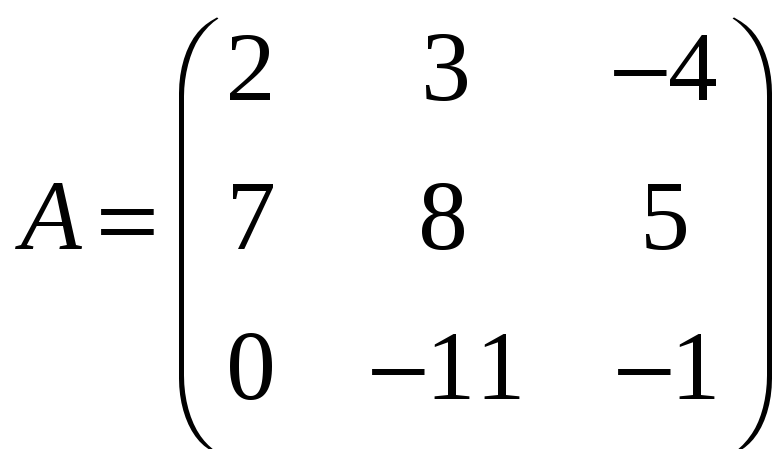 ;
в)
;
в)
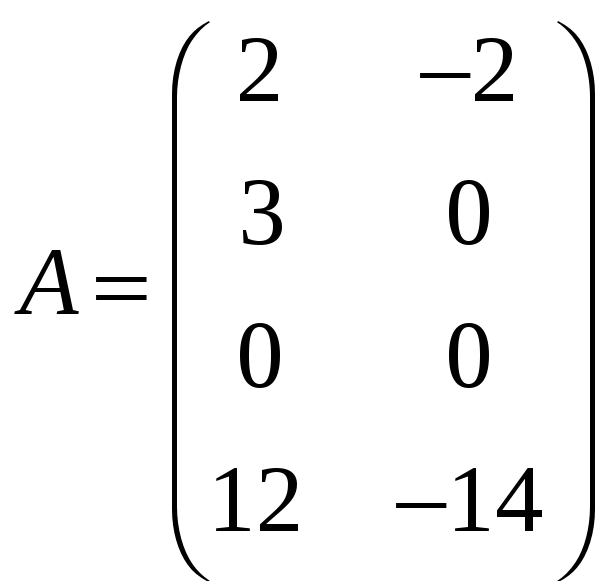 ;
г)
;
г)
![]() .
.
Квадратна
матриця A
називається
симетричною,
якщо
![]() .
.
Якщо
![]()
симетрична матриця, то з означення
випливає, що
симетрична матриця, то з означення
випливає, що
![]() для всіх
для всіх
![]() .
.
Наприклад, симетричними є такі матриці:
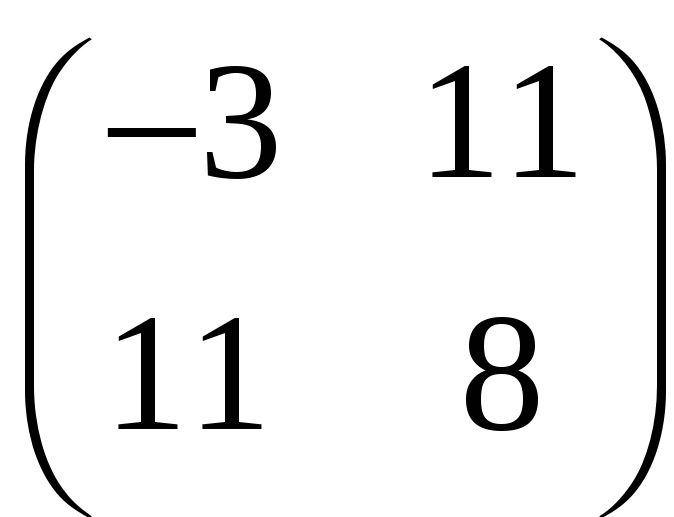 ,
,
 ,
,
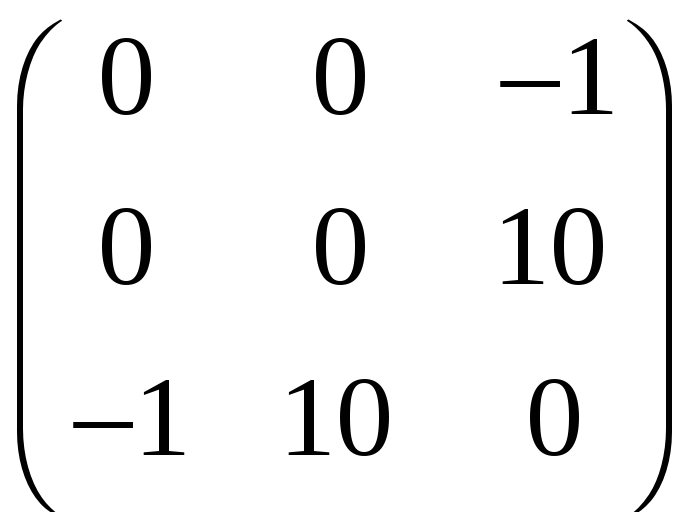 .
.
Зрозуміло, що одинична, діагональна та нульова матриці є симетричними.
Квадратна
матриця A називається
кососиметричною,
якщо
![]() .
.
Якщо
![]()
кососиметрична матриця, то
кососиметрична матриця, то
![]() для всіх
для всіх
![]() .
Звідси виходить, що всі елементи головної
діагоналі кососиметричної матриці
дорівнюють нулю.
.
Звідси виходить, що всі елементи головної
діагоналі кососиметричної матриці
дорівнюють нулю.
Кососиметричні, наприклад, такі матриці:
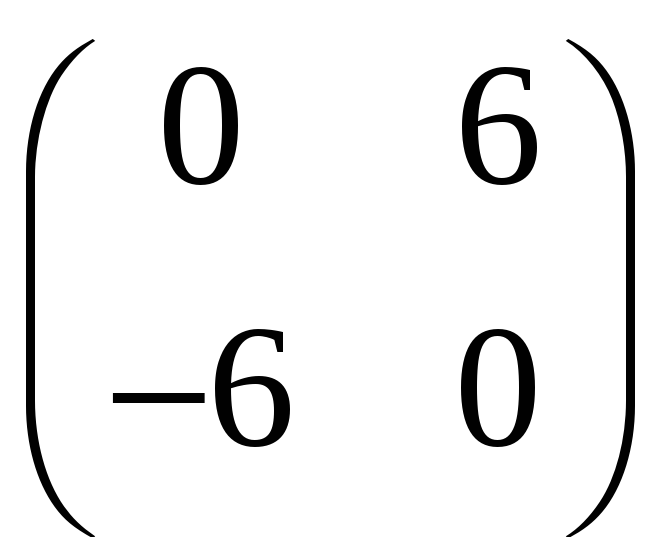 ,
,
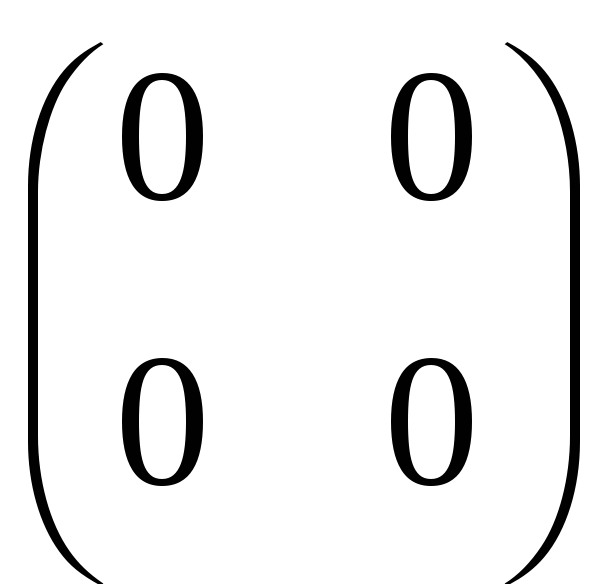 ,
,
 .
.
Приклад
3.11.
Доведемо, що
для будь-якої квадратної матриці A
матриця
![]() є симетричною, а матриця
є симетричною, а матриця
![]() – кососиметричною.
– кососиметричною.
Із властивостей операції транспонування маємо:
![]() ,
,
![]() .
.
Задача 3.33. Довести, що будь-яка квадратна матриця може єдиним способом бути подана у вигляді суми симетричної та кососиметричної матриць.
Задача
3.34.
Довести,
що коли В – симетрична (кососиметрична)
матриця, то матриці
![]() ,
,
![]() ,
,
![]() є симетричними (кососиметричними).
є симетричними (кососиметричними).
Задача
3.35.
Нехай A
– матриця розміру k
n.
Довести, що добутки
![]() і
і
![]() є визначеними і вказати їх розміри.
Довести, що ці добутки є симетричними
матрицями.
є визначеними і вказати їх розміри.
Довести, що ці добутки є симетричними
матрицями.
Задача 3.36. Довести, що добуток двох симетричних (кососиметричних) матриць тоді і тільки тоді буде симетричною матрицею, коли ці матриці переставні.
4. Обернена матриця
Квадратна матриця A називається виродженою, якщо її визначник дорівнює нулю, і невиродженою – у протилежному випадку.
Наприклад, якщо
 ,
,
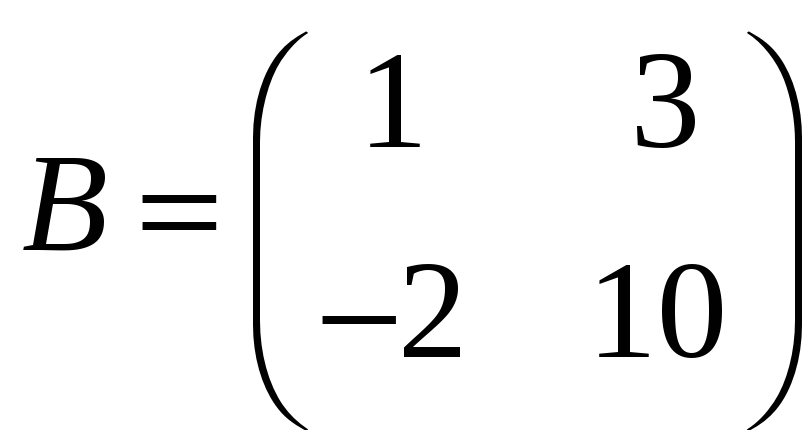 ,
,
то A – вироджена, а B – невироджена.
Нехай
![]() – квадратна матриця порядку
n.
Матриця B
називається
оберненою
для
матриці A,
якщо
– квадратна матриця порядку
n.
Матриця B
називається
оберненою
для
матриці A,
якщо
AB = BA = E,
де E – одинична матриця.
Якщо квадратна матриця A має обернену, то ця обернена матриця єдина. Матрицю, обернену до A, позначають A–1.
Приклад
3.12.
Покажемо,що для матриці
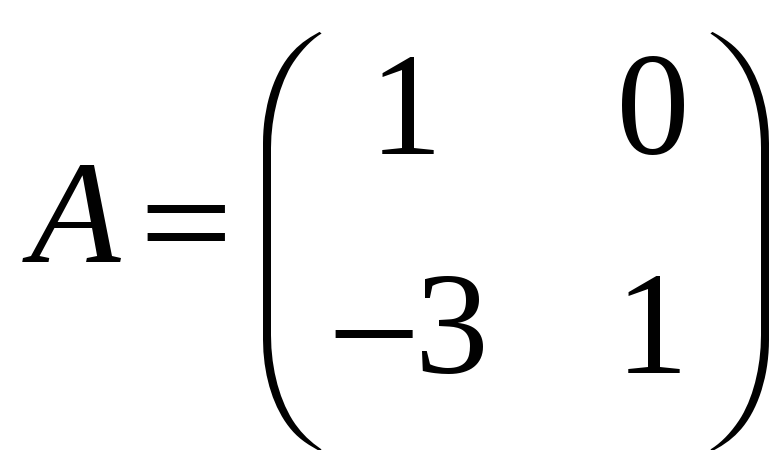 оберненою є матриця
оберненою є матриця
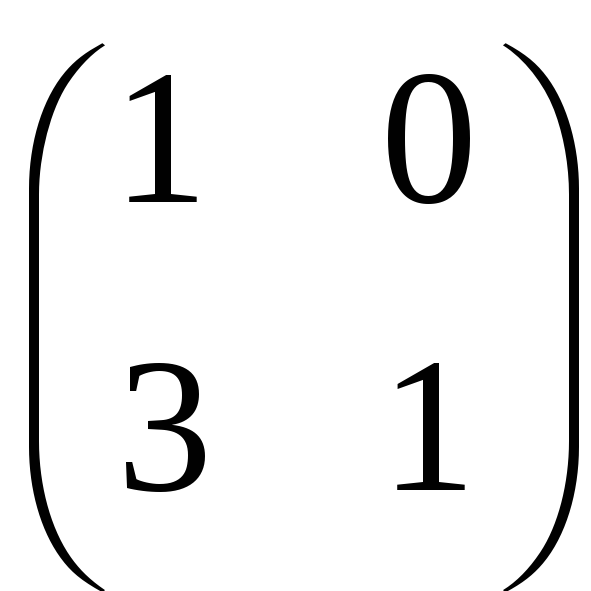 .
.
Дійсно,
 .
.
Твердження.
Якщо
для квадратної матриці A
існує
обернена матриця
A–1,
то A
є
невиродженою і
![]() .
.
Доведення. Нехай матриця A має обернену A–1. Тоді
![]()
![]() .
.
Теорема
.
Нехай A
– квадратна матриця порядку n.
Матриця
A тоді й тільки тоді має обернену матрицю
A–1,
коли вона є невиродженою. Якщо
![]() ,
то
,
то
![]() ,
де
,
де
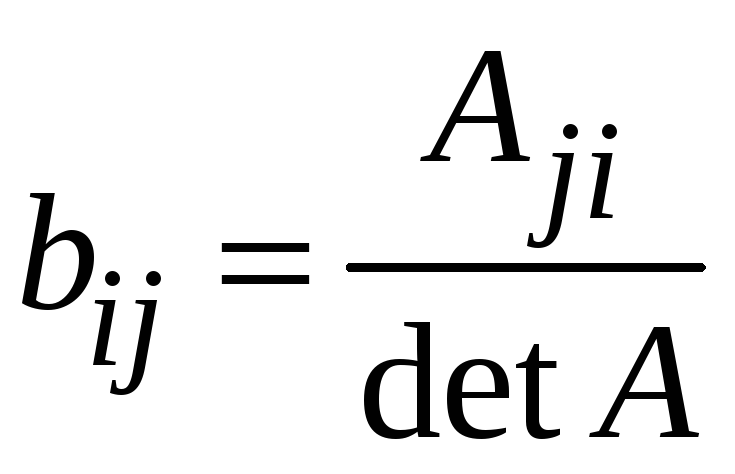 (1
i,j
n).
(1
i,j
n).
Доведення дивись, напр., в [3].
З теореми виходить, що коли
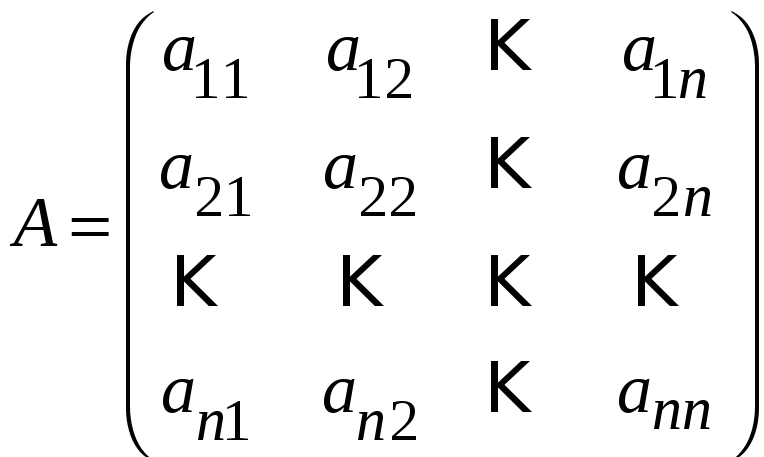 і
detA
≠ 0,
і
detA
≠ 0,
то
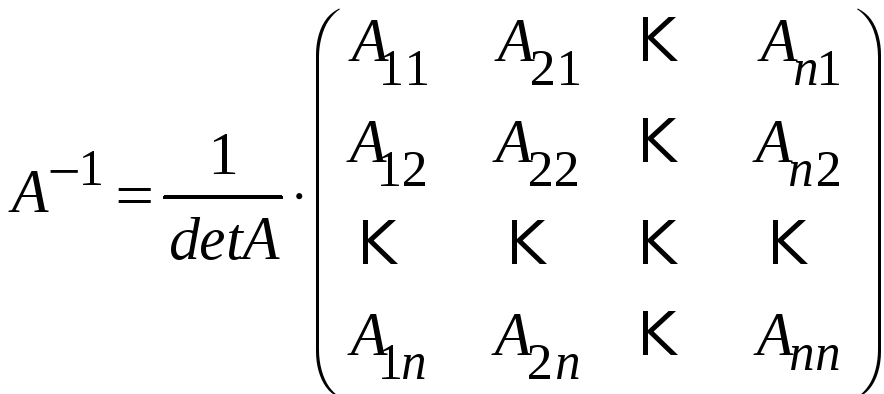 .
.
Матриця
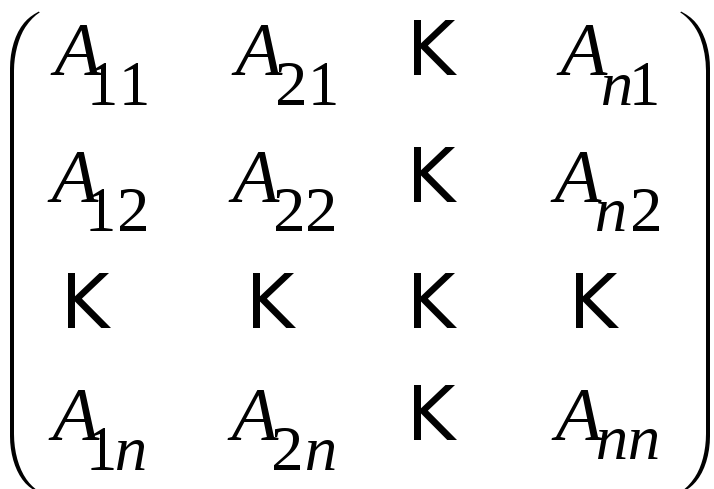
називається
приєднаною
для матриці A
і позначається
![]() .
Матриця
.
Матриця
![]() є
транспонованою до матриці, складеної
з алгебраїчних доповнень елементів
матриці A
в їх природному розміщенні, Отже,
є
транспонованою до матриці, складеної
з алгебраїчних доповнень елементів
матриці A
в їх природному розміщенні, Отже,
![]() .
.
Знаходження матриці A–1 можна розділити на такі етапи:
1. Знаходимо detA. Якщо detA = 0, то A–1 не існує. Якщо detA ≠ 0, то переходимо до 2.
2.
Обчислюємо алгебраїчні доповнення
![]() для всіх елементів
для всіх елементів
![]() матриці
матриці
A ( 1 i,j n).
3.
Будуємо приєднану
матрицю
![]() .
.
4.
Множимо всі елементи матриці
![]() на
на
![]() .
.
Відзначимо деякі властивості оберненої матриці.
1. (A–1)–1 = A.
2. Якщо для квадратних матриць A і B однакових порядків існують обернені матриці A–1 і B–1, то для добутку AB також існує обернена матриця і
(AB)–1 = B–1A–1.
3. (A–1)t = (At) –1.
Доведемо властивість 2. Нехай для квадратних матриць A і B однакових порядків існують обернені матриці A–1 і B–1. Тоді detA ≠ 0 і detB ≠ 0.
detAB = detAdetB detAB ≠ 0,
отже, існує (AB)–1.
(AB)(B–1A–1) = A(BB–1)A–1 = AEA–1 = AA–1 = E,
а, значить, (AB)–1 = B–1A–1.
Властивості 1 і 3 пропонуються для самостійного доведення.
Приклад
3.13.
Знайдемо
обернену матрицю для матриці
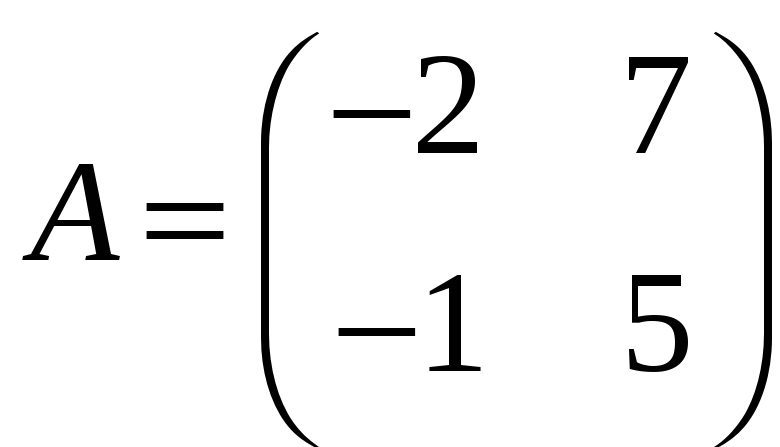 .
.
1. Оскільки detA = –3, то матриця A–1 існує.
2.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
3.
Побудуємо приєднану
матрицю:
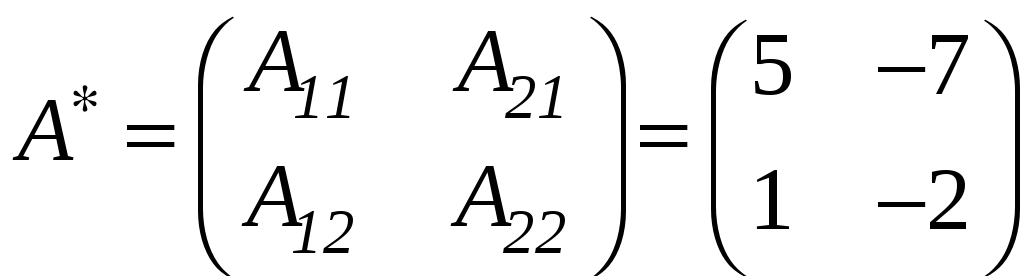 .
.
4.
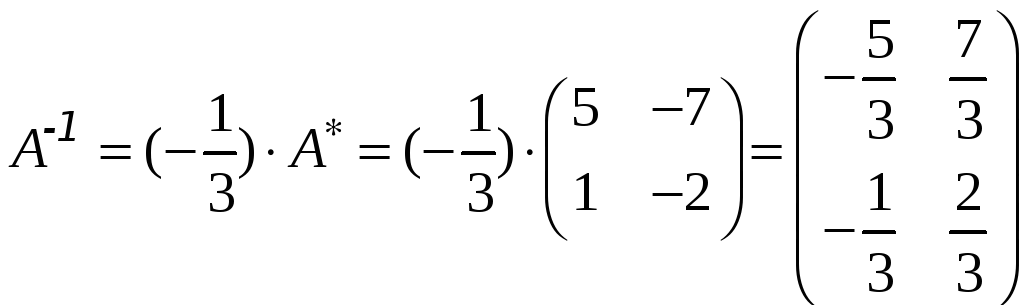 .
.
Упевнимось в тому, що обернена матриця A–1 знайдена правильно.
 .
.
Приклад
3.14.
До матриці
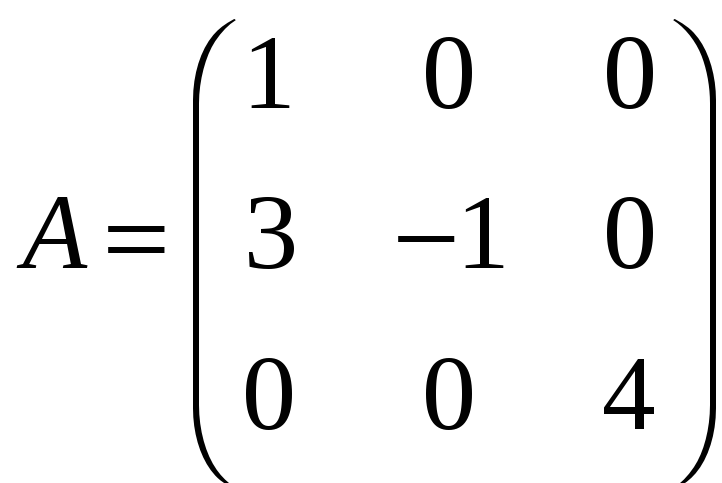 знайдемо
обернену матрицю
A–1.
знайдемо
обернену матрицю
A–1.
1. detA = –4, а, значить матриця, обернена до A існує.
2.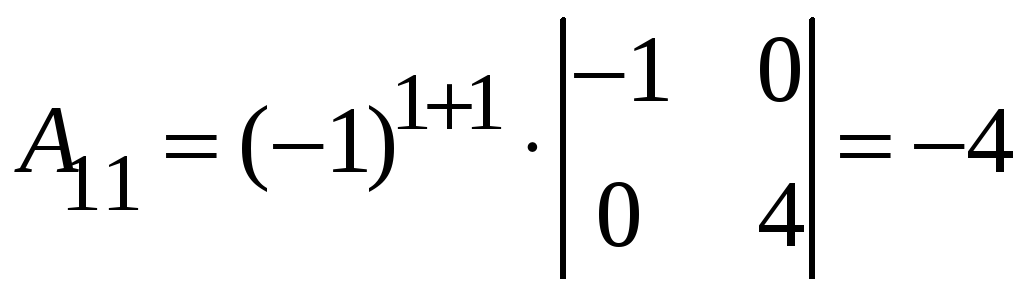 ,
,
 ,
,
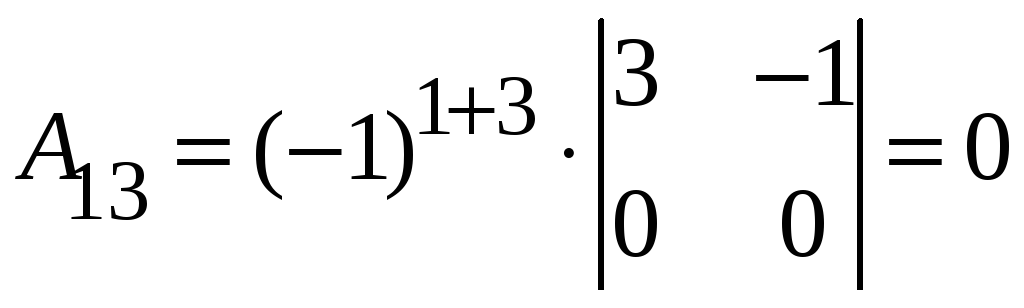 ,
,
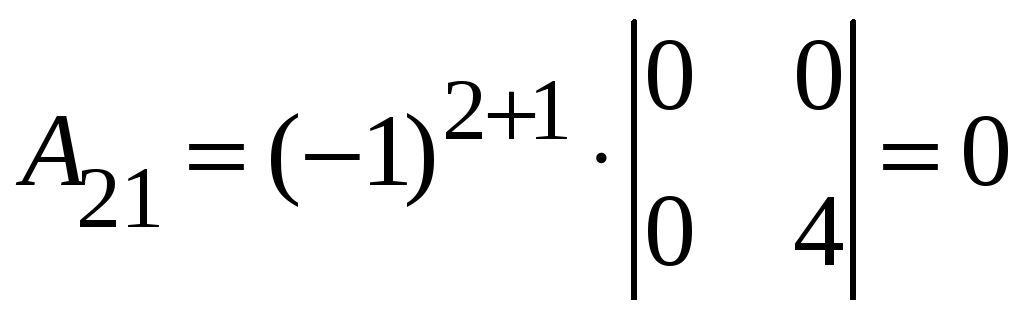 ,
,
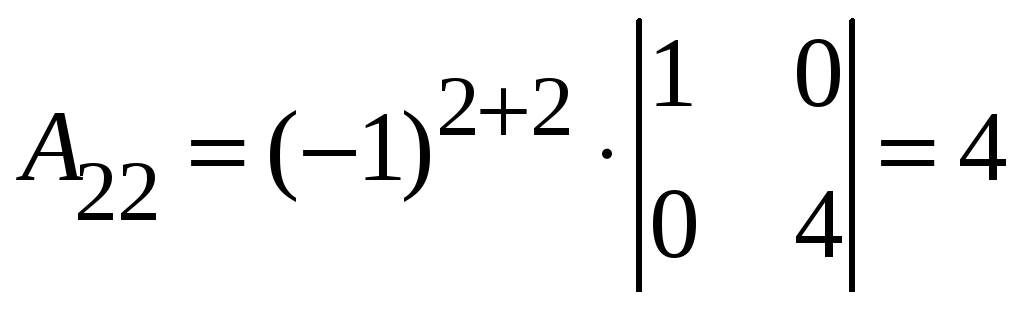 ,
,
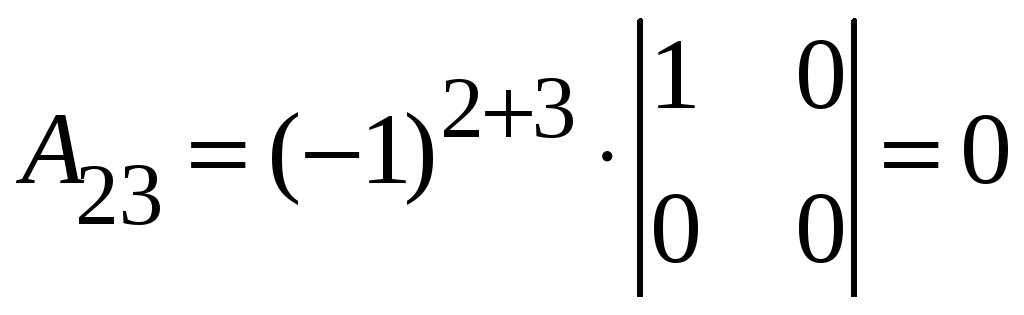 ,
,
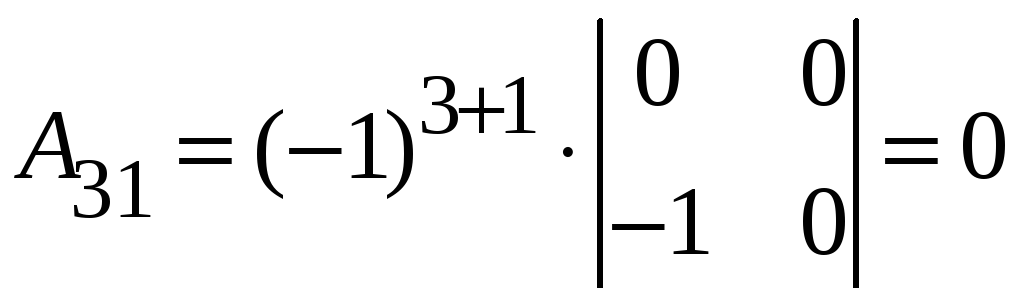 ,
,
 ,
,
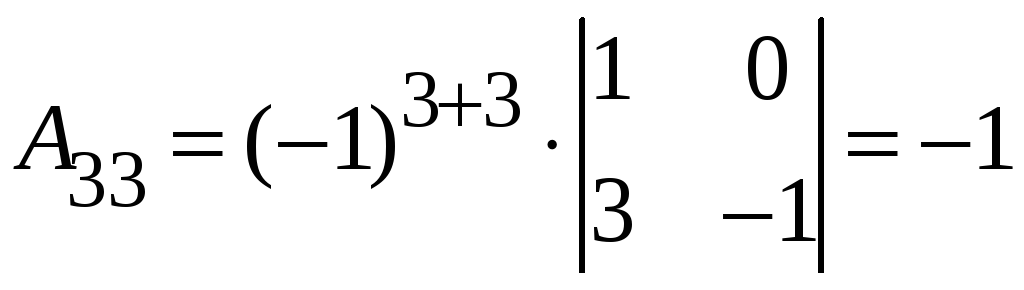 .
.
3.
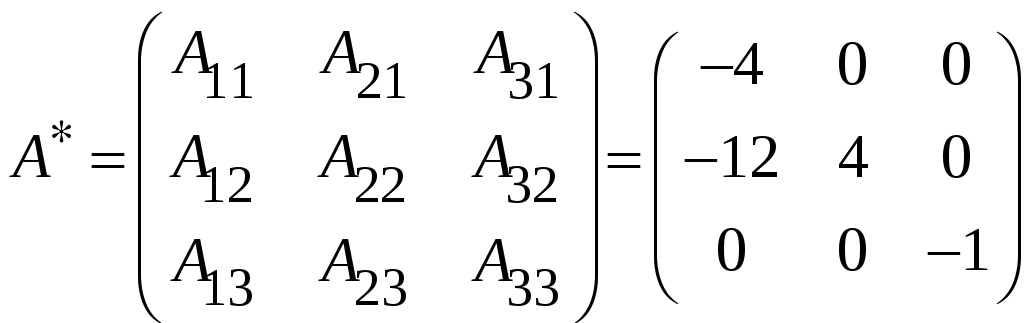 .
.
4.
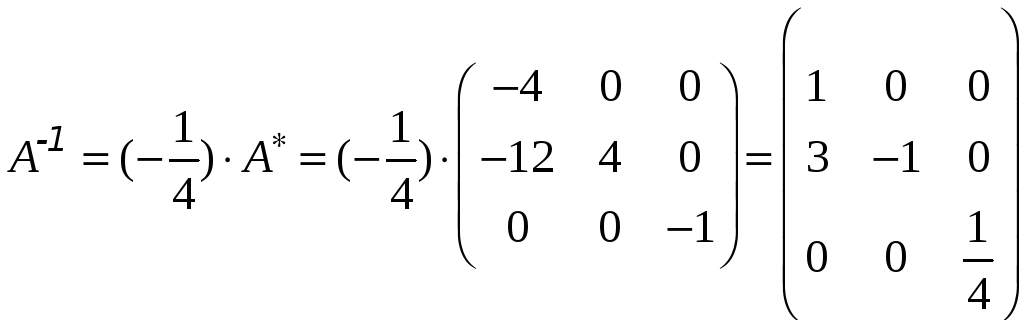 .
.
Задача 3.37. З’ясувати, чи існує до матриці A обернена матриця. Якщо так, то знайти A–1.
а)
 ;
б)
;
б)
 ;
в)
;
в)
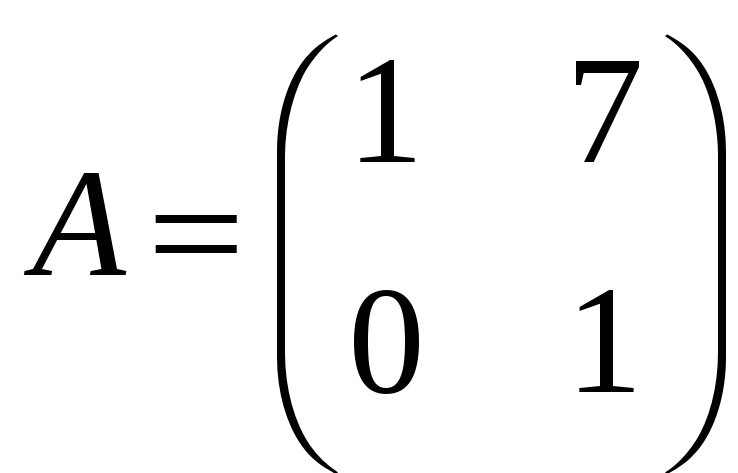 ;
г)
;
г)
 ;
;
д)
 ;
е)
;
е)
 ;
є)
;
є)
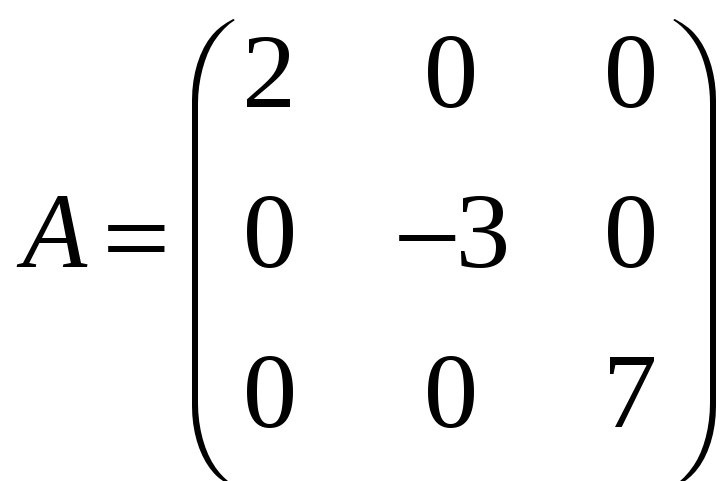 ;
ж)
;
ж)
 ;
з)
;
з)
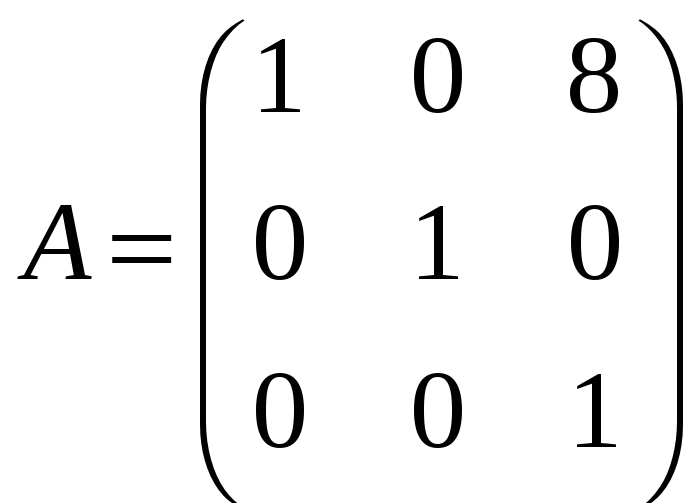 ;
і)
;
і)
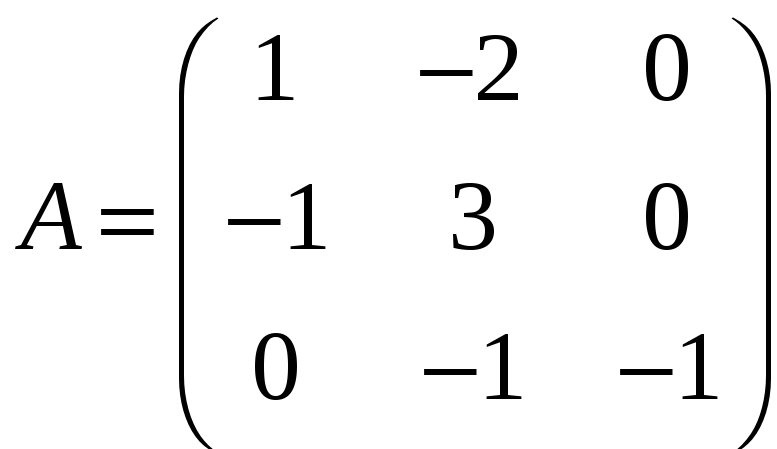 ;
к)
;
к)
 ;
;
л)
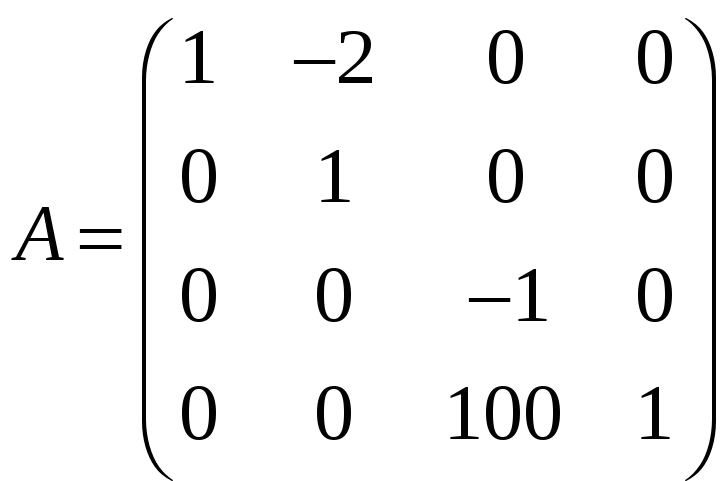 .
.
Задача 3.38. Нехай A = diag( a1, a2, , an ). За якої умови до матриці A існує обернена матриця і чому дорівнюють елементи матриці A–1, коли вона існує?
Задача 3.39. A – квадратна матриця, така що A = A–1. Знайти матрицю B, якщо B = (A + E)(A – E).
Задача 3.40. Знайти всі квадратні матриці A порядку n, такі що
A = A–1 і A15 = E.
Задача 3.41. Знайти A–1, якщо
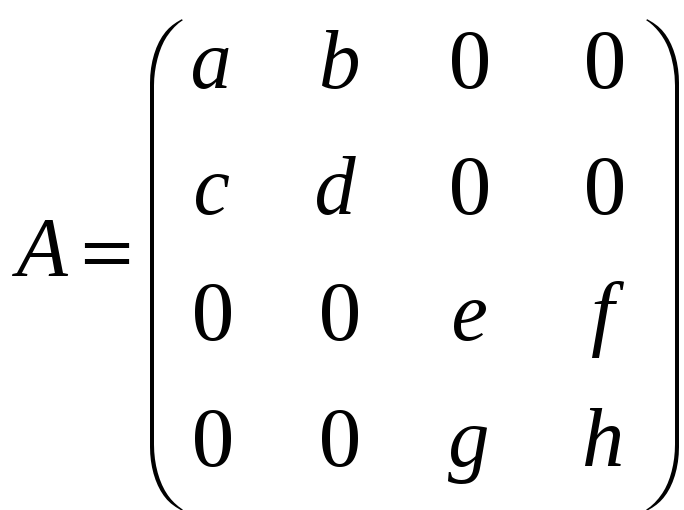 ,
,
причому ad – bc = fg – eh =1.
Розглянемо метод визначення оберненої матриці за допомогою елементарних перетворень.
Елементарними перетвореннями матриці вважаються:
1. Додавання до якого-небудь рядка (стовпця) іншого рядка (стовпця), помно-женого на деяке число.
2. Множення всіх елементів якого-небудь рядка (стовпця) на число, відмінне від нуля.
3. Переставляння місцями рядків (стовпців).
Нехай A – деяка невироджена матриця. Будемо здійснювати елементарні перетворення над рядками (або стовпцями) A, щоб звести її до одиничної. Якщо ці елементарні перетворення в тій самій послідовністі здійснити і над одиничною матрицею E, то вона перейде в матрицю A–1.
Зауваження. При застосуванні цього методу елементарні перетворення роблять або тільки над рядками або тільки над стовпцями матриці.
Приклад
3.15.
До матриці A
=
 знайдемо обернену за допомогою
елементарних перетворень.
знайдемо обернену за допомогою
елементарних перетворень.
Оскільки detA = –1 0, то матриця A–1 існує. Запишемо поряд з матрицею A одиничну матрицю E і будемо вказувати елементарне перетворення, яке буде здійснюватись над A. Таке ж саме перетворення будемо робити і над E, а нижче записувати матриці, змінені в результаті цього перетворення. У цьому прикладі елементарні перетворення будемо виконувати над стовпцями матриць A і E.
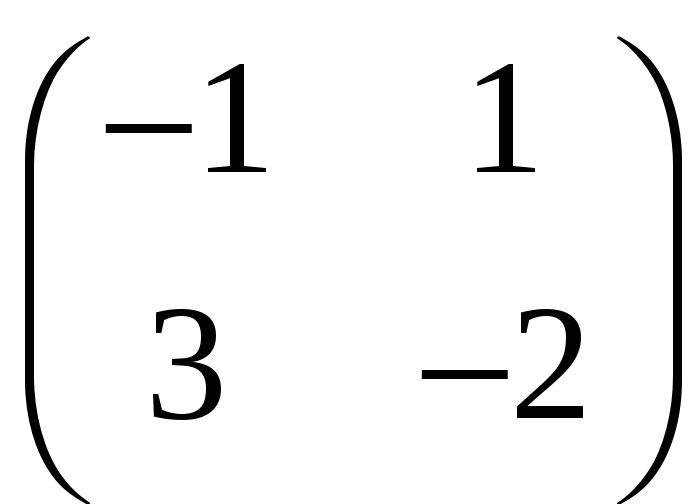
 .
.
До другого стовпця додамо перший
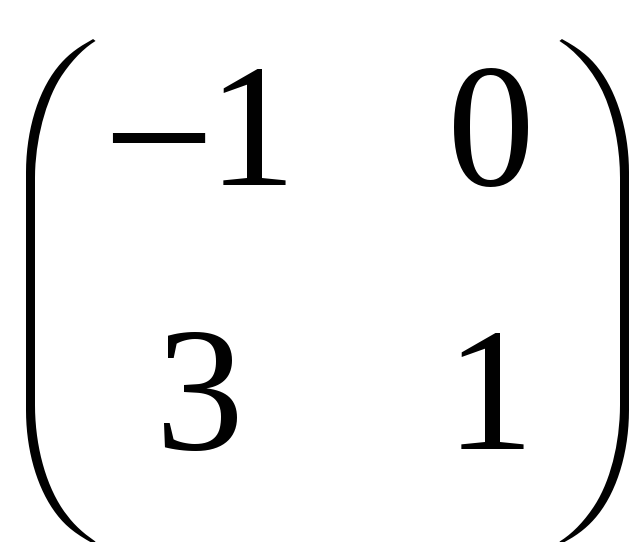
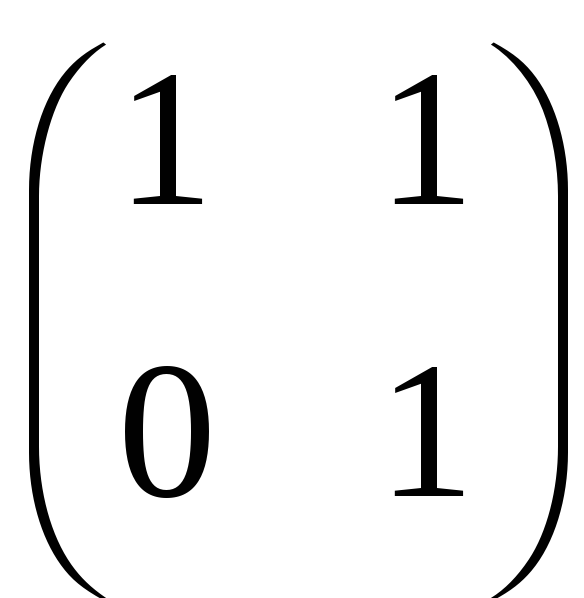 .
.
До першого стовпця додамо другий, помножений на (–3)
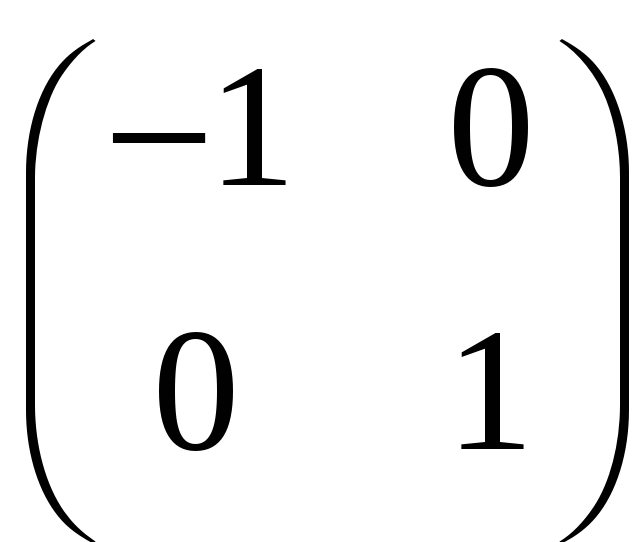
 .
.
Перший стовпець помножимо на (–1)

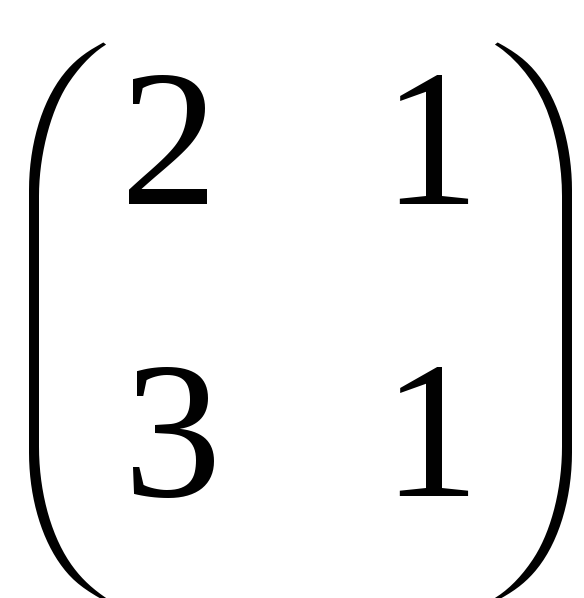 .
.
Отже,
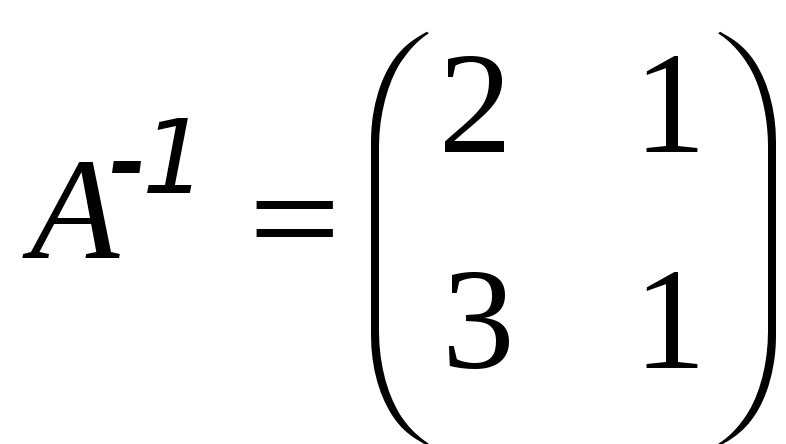 .
.
Приклад
3.16.
Знайдемо обернену матрицю до матриці
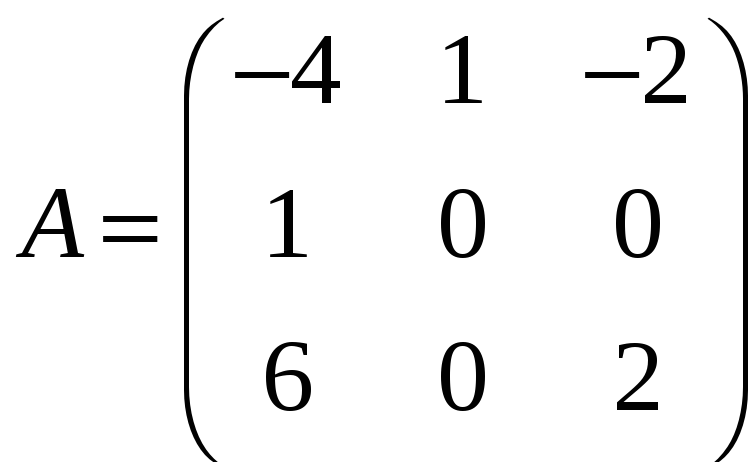 .
.
Матриця A є невиродженою, отже, A–1 існує. Елементарні перетворення будемо здійснювати над рядками матриць.

 .
.
Поміняємо місцями перший і другий рядки:

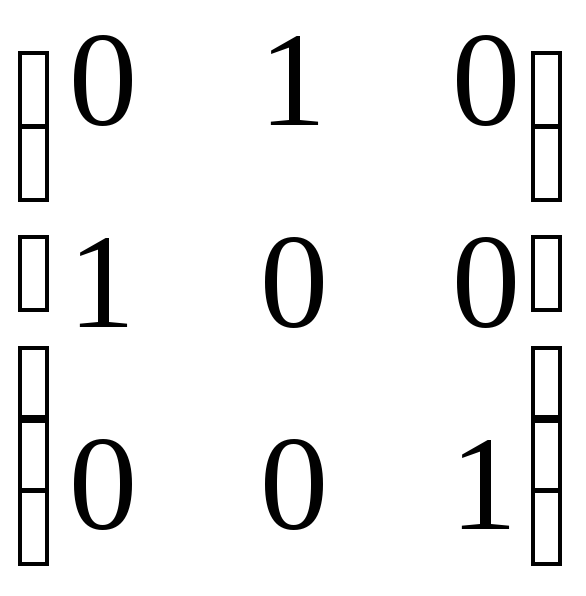 .
.
До другого рядка додамо перший, помножений на 4, а до третього рядка –перший, помножений на (–6)
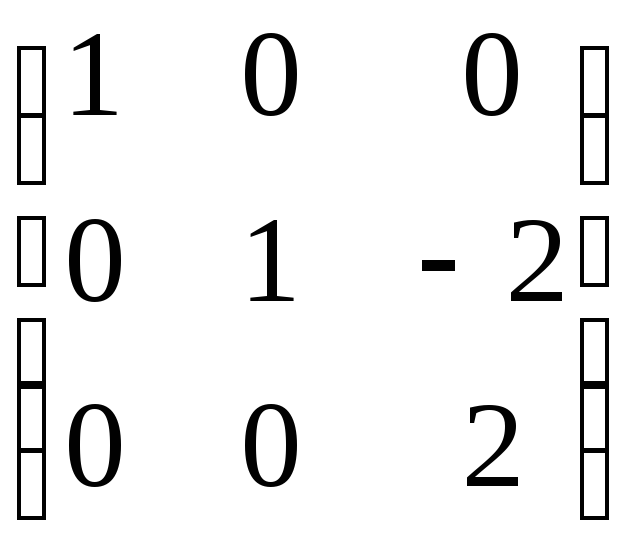
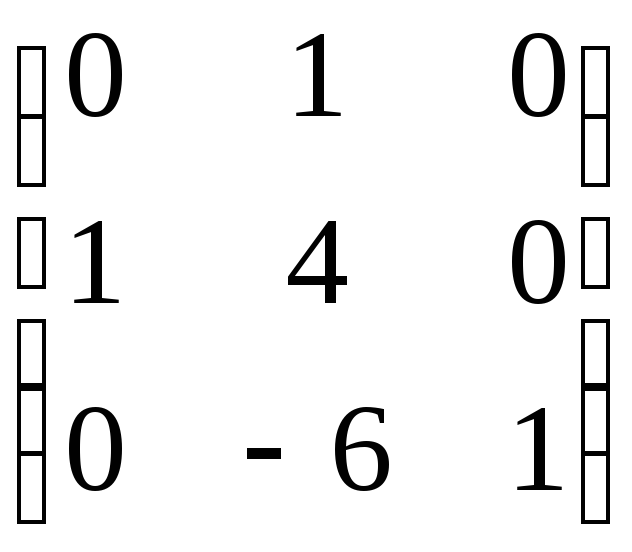 .
.
До другого рядка додамо третій

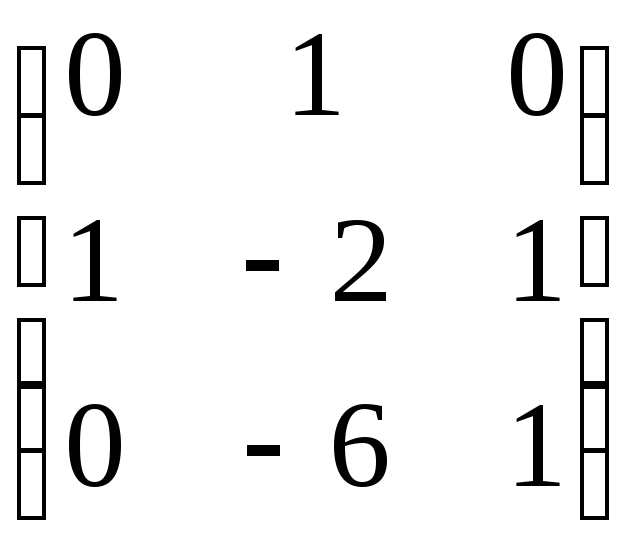 .
.
Третій рядок поділимо на 2
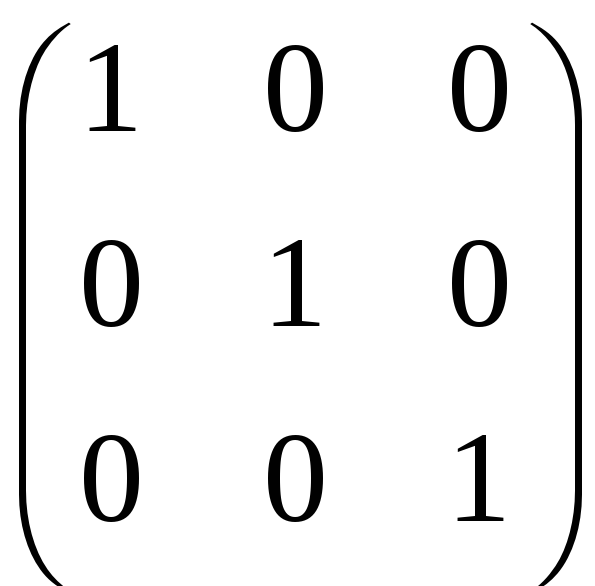
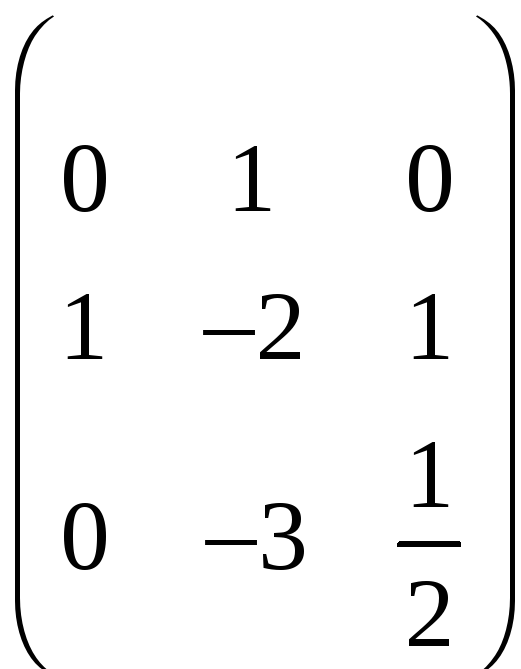 .
.
Ми отримали, що
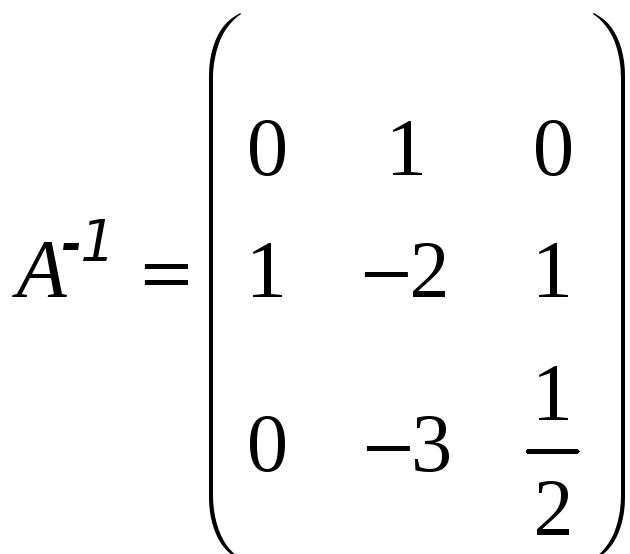 .
.
Приклад
3.17.
Нехай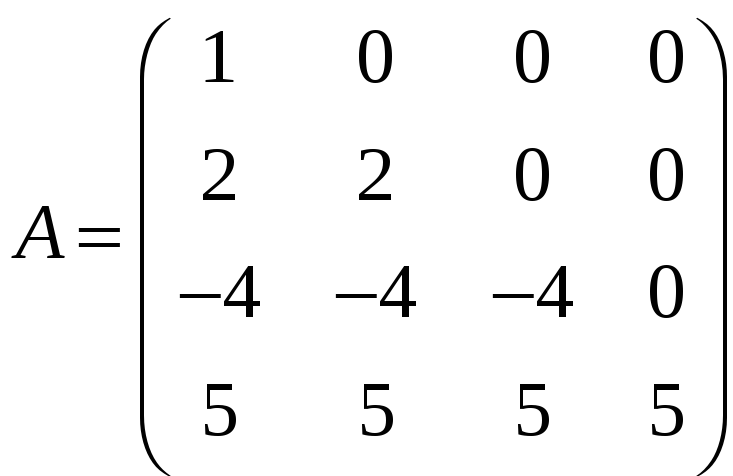 .
Знайдемо обернену матрицю A–1.
.
Знайдемо обернену матрицю A–1.
Зробимо
над рядками матриць A
і
E
такі
елементарні перетворення: 1) до четвертого
рядка додамо третій, помножений на
![]() ;
2) до третього рядка додамо другий,
помножений на 2; 3) до другого рядка додамо
перший, помножений на
;
2) до третього рядка додамо другий,
помножений на 2; 3) до другого рядка додамо
перший, помножений на
(–2); 4) другий рядок поділимо на 2, третій – на (– 4), а четвертий – на 5.
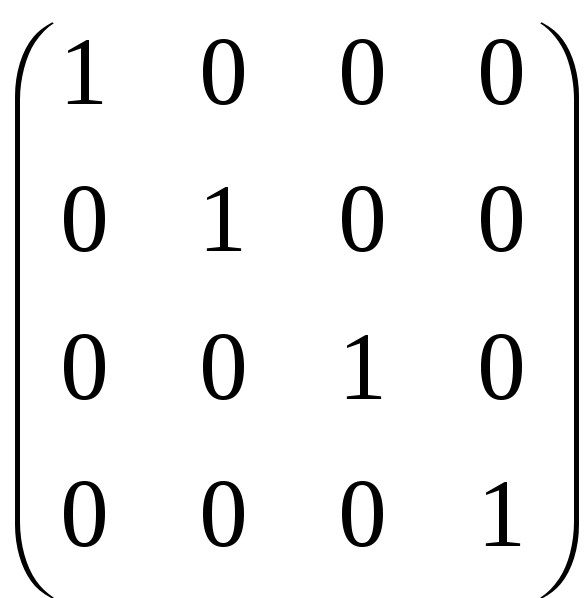
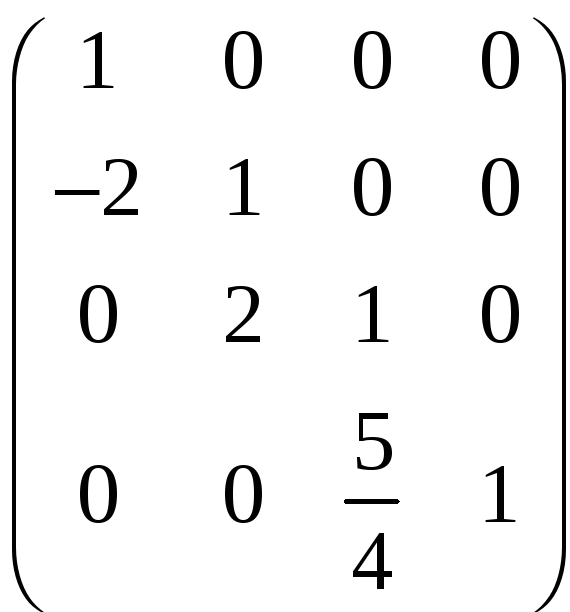
Будемо мати:
 |
|
![]()
 |
|
![]()
![]()
 |
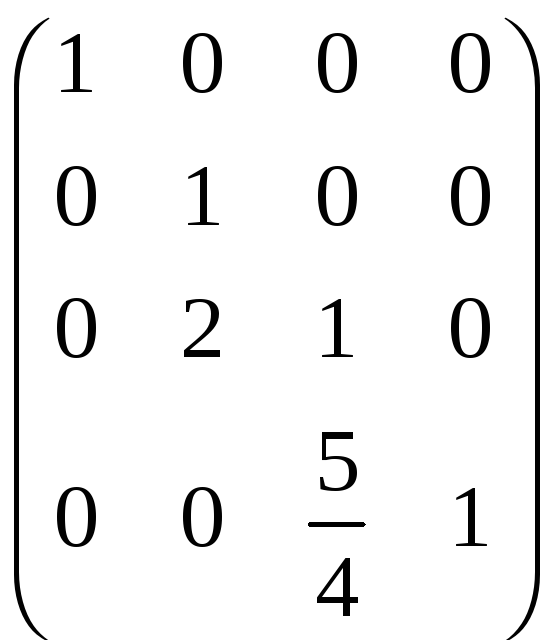
|
![]()
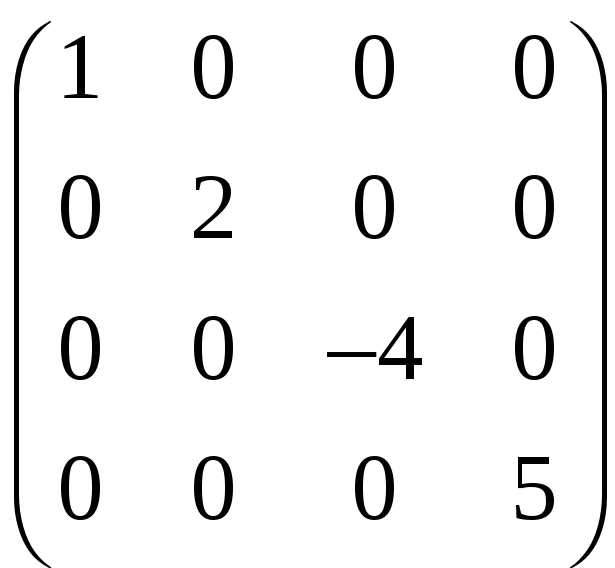 |
|
![]()
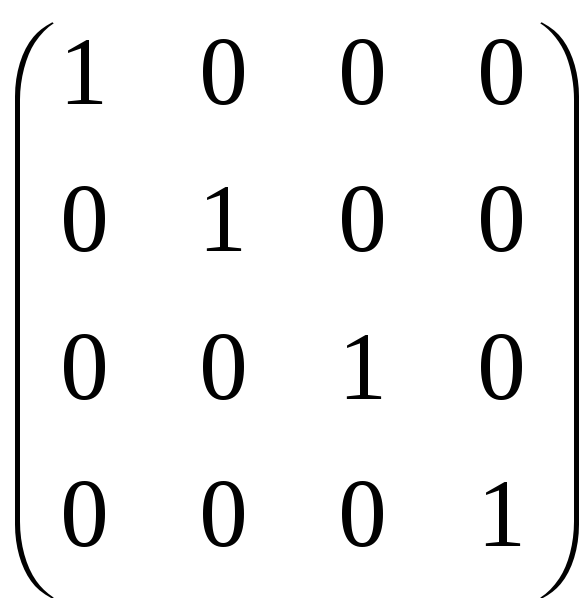 |
|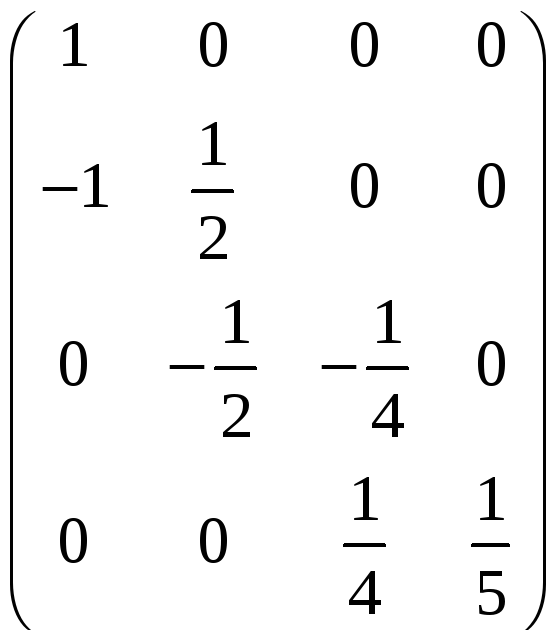 ,
а, значить,
,
а, значить,
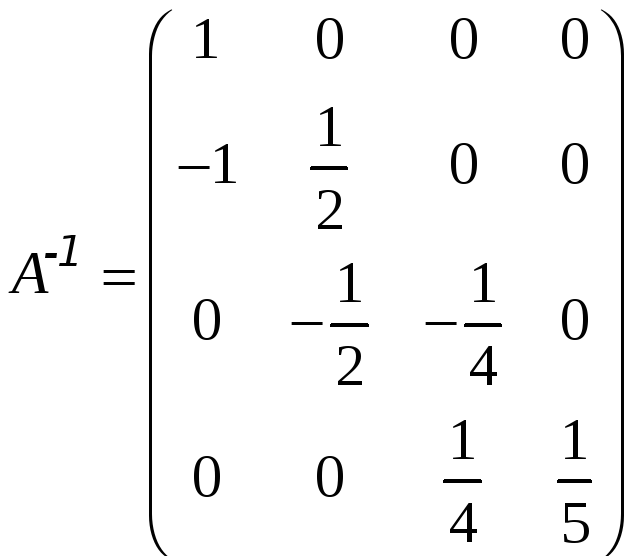 .
.
Задача 3.42. З’ясувати, які з поданих матриць мають обернені і за допомогою елементарних перетворень знайти обернені матриці:
а)
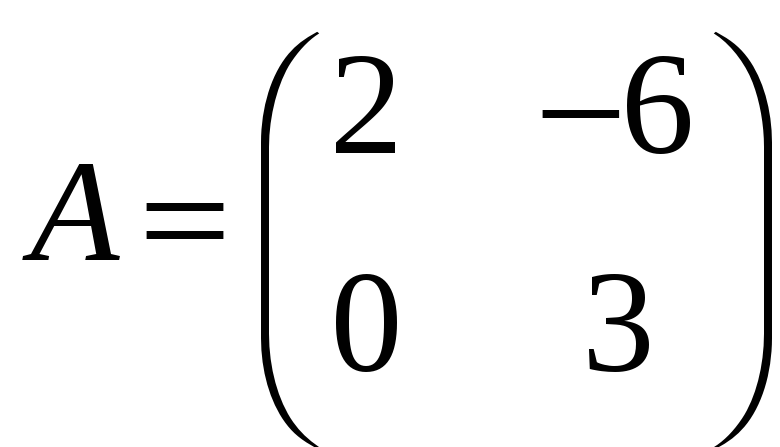 ;
б)
;
б)
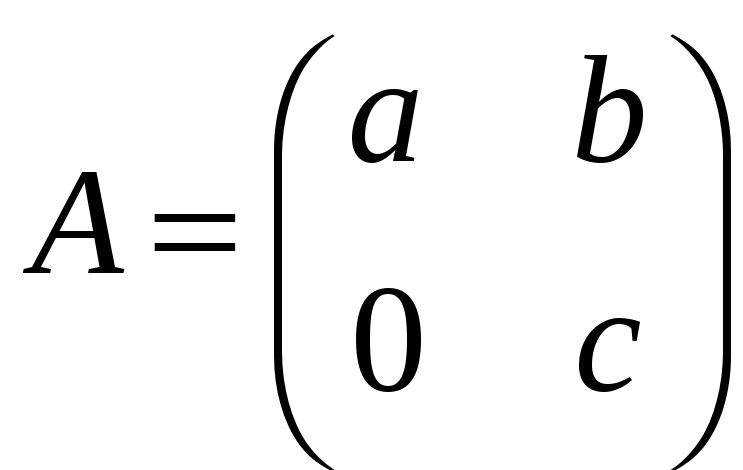 ;
в)
;
в)
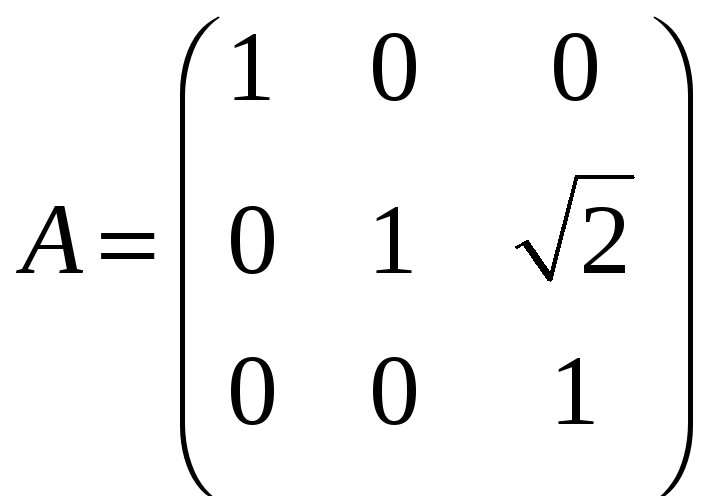 ;
г)
;
г)
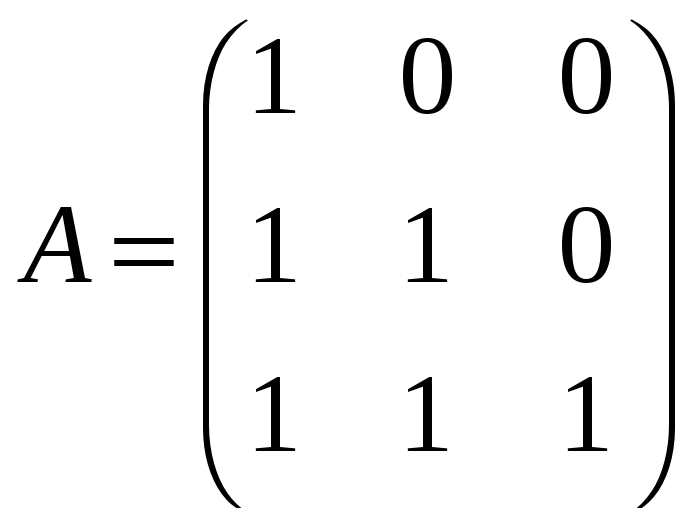 ;
;
д)
 ;
е)
;
е)
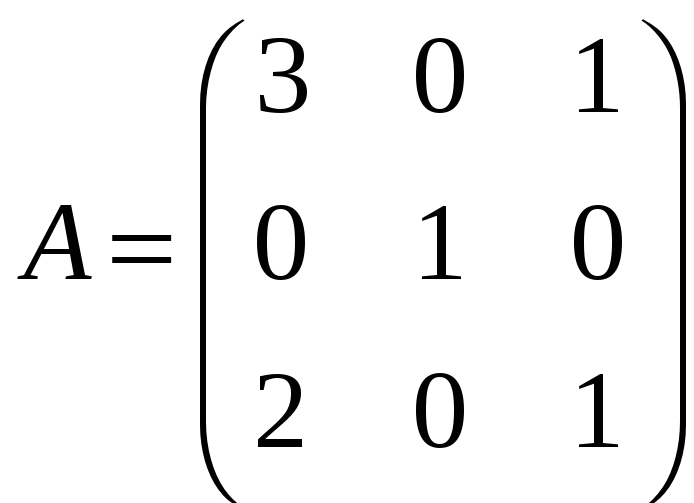 ;
є)
;
є)
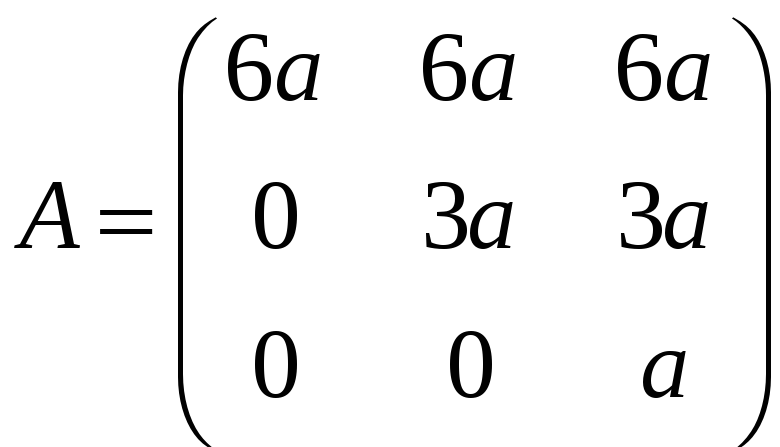 ;
;
ж)
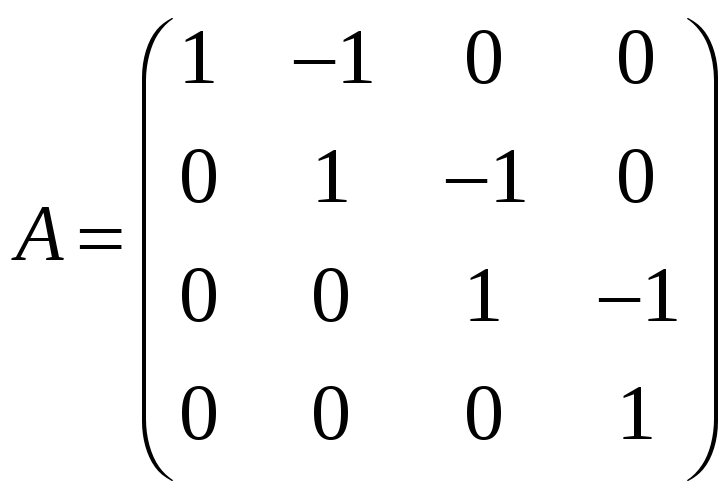 ;
з)
;
з)
 ;
і)
;
і)
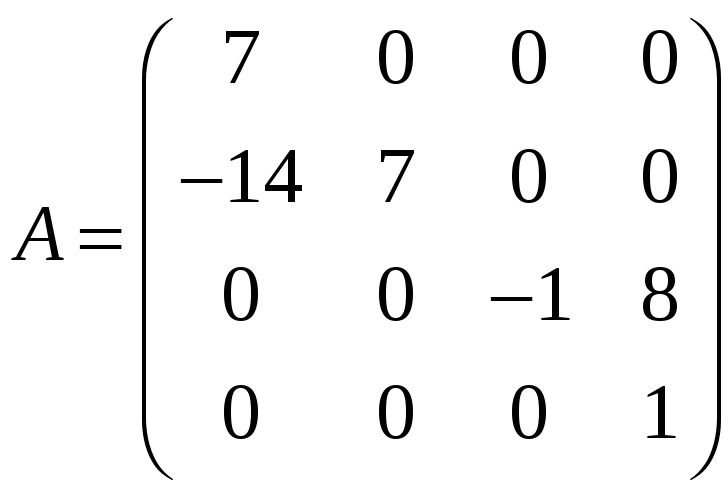 ;
;
к)
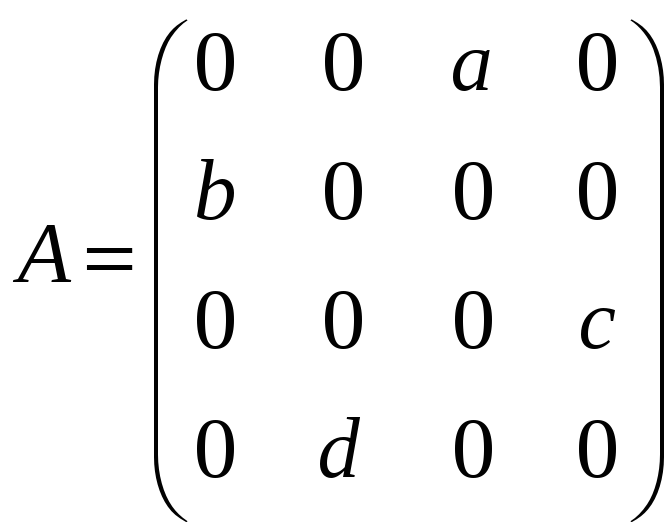 ;
;
Матриці, подані нижче, мають порядок n.
л)
 ;
м)
;
м)
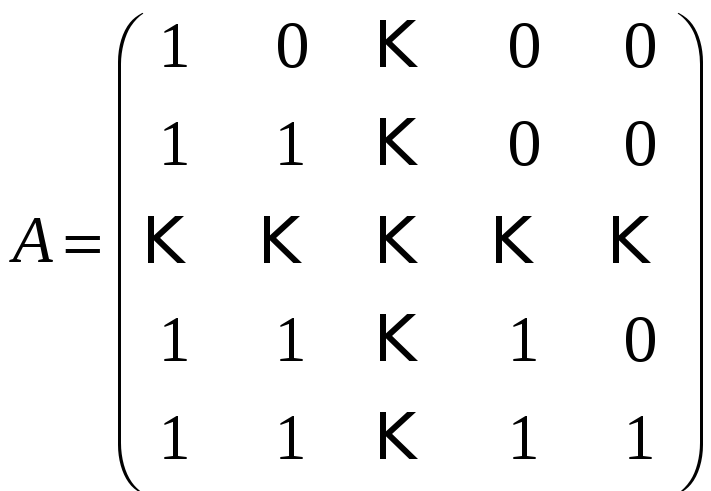 .
.
Задача 3.43. Як зміниться обернена матриця A–1, якщо:
а) у матриці A k-й та m-й стовпці переставити місцями?
б) у матриці A k-й та m-й рядки переставити місцями?
в)
у матриці A
k-й
стовпець помножити на число
![]() ?
?
г)
у матриці A
до k-го
рядка додати m-й
рядок, помножений на число
![]() ?
?
Приклад 3.18. Розв’яжемо матричне рівняння
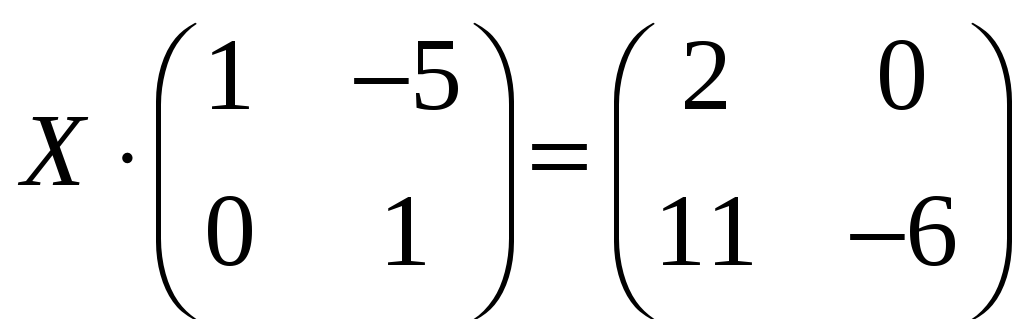 .
.
Із
правил множення матриць виходить, що X
– квадратна
матриця порядку 2. Позначимо
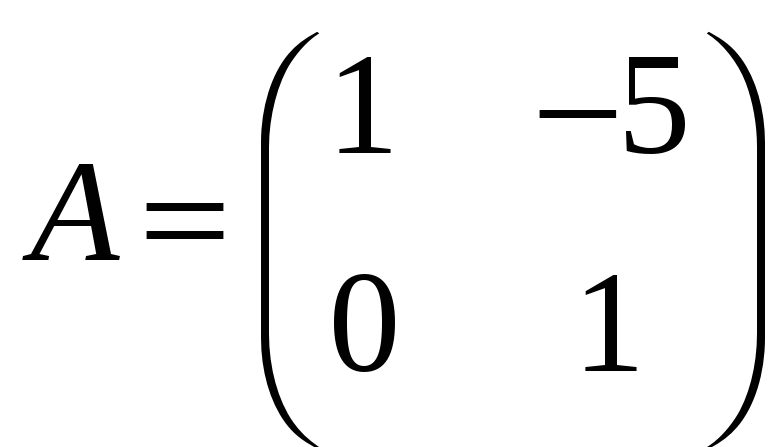 ,
,
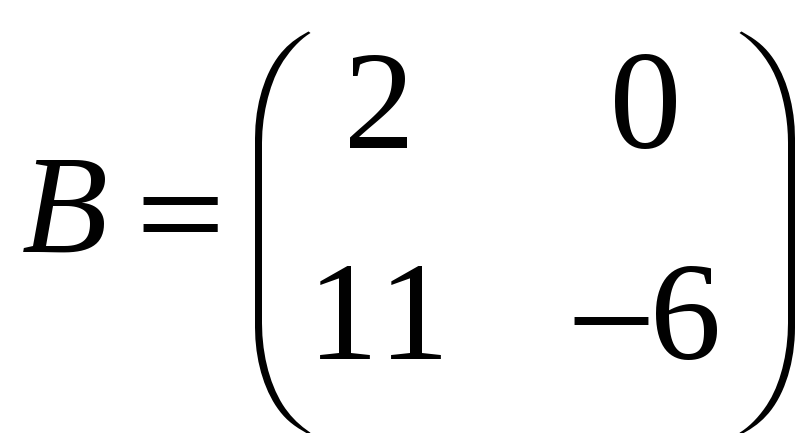 .
Обидві частини рівняння
.
Обидві частини рівняння
XA = B
зліва помножимо на матрицю A–1. Отримаємо
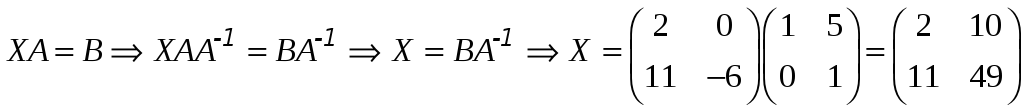 .
.
Задача 3.44. Розв’язати матричні рівняння:
а)
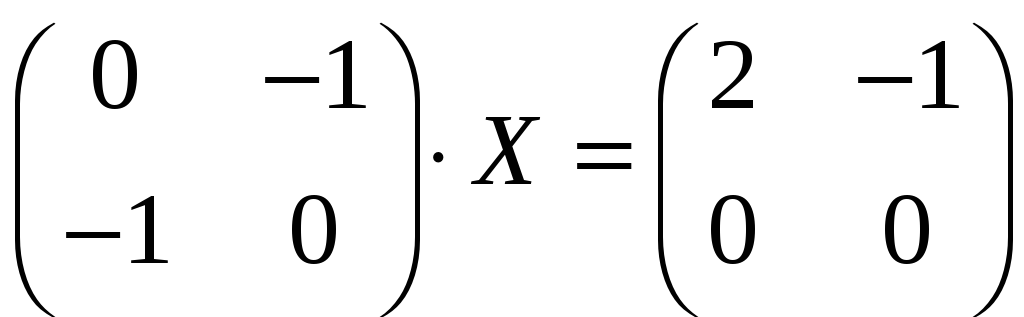 ;
б)
;
б)
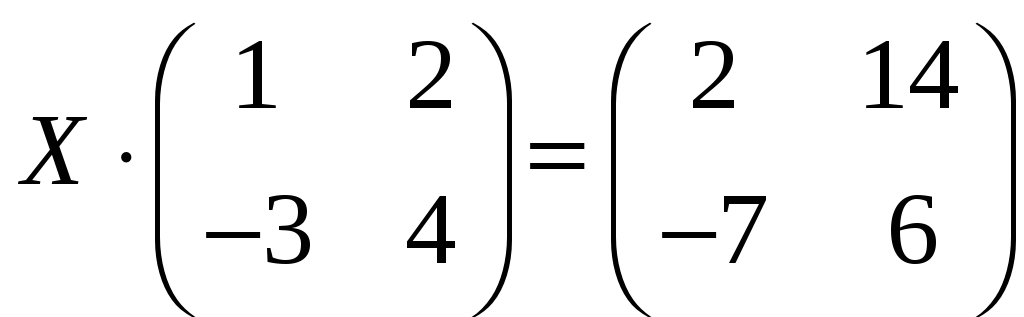 ;
;
в)
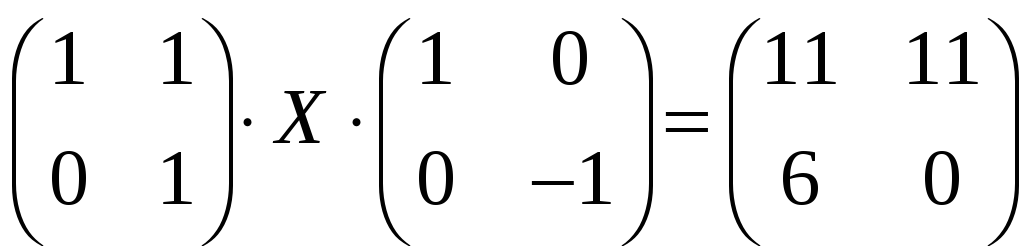 ;
;
г) .
.
