Методичка №2

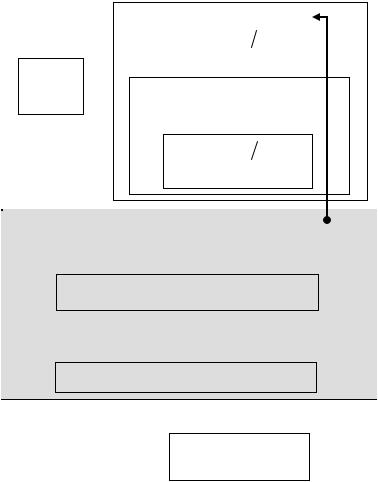
При такій схемі часткового вибору головного елемента по стовпцю загальний алгоритм Гауса не змінюється. Необхідно лише на кожному кроці методу здійснювати сортування по головному елементу.

Загальний алгоритм методу Гауса з вибором головного елемента по стовпцю

для k =

1, n

стовпцеві сортування

для i, j =

Yk

= Pk Vkk

1, n

Прямий

для i =

Vi, j

= Ai, j

k +1, n

хід:

Pi = Pi −Vik Yk

P = B

i

i

для

j =

k +1,n

Ckj

=Vkj Vkk ;

Vij =Vij −Vik Ckj

стовпцеві сортування

max =

Vkk

; w = k

для l =

k +1, n

якщо max <

Vlk

→ { max =

Vlk

; w =l }

value = Pk ;

Pk = Pw ;

Pw =value

для d =

1,n

value =Vkd ; Vkd =Vwd ; Vwd =value

Оберне-

для i =

n −1,1

X n

=Yn

n

ний хід:

X i =Yi − ∑Cij X j

j=i+1

9

Опис алгоритму

1.Прямий хід методу. Резервуємо (копіюємо) базові матриці A та B у відповідні матриці V та P . Вхідні матриці A та B нам необхідні

для кінцевої перевірки результату. Протягом виконання алгоритму ми працюємо з копіями вхідних матриць.

2.Далі в трьох циклах виконується перетворення початкової матриці A до трикутного вигляду матриці C та відповідне перетворення

правих частин системи B . Зазначимо, що на кожному кроці першого циклу по змінній k виконуємо процедуру стовпцевого сортування по головним елементам. Тобто, відшукуємо максимальне значення по модулю головного елемента, а потім міняємо місцями рядки в матриці V та P (копії матриці A та B ). Змінна w визначає номер рядка головного елемента, а value використовується як проміжна змінна.

3.Обернений хід. Спершу присвоюємо значення для останнього невідомого xn , а потім в циклі відшукуємо усі решта невідомі.

4.Для перевірки вірності роботи алгоритму підставляємо наші знайдені x1 , x2 , ..., xn в систему (1.1). Обчислені ліві частини рівнянь повинні відповідати правим значенням елементів вектора B .

3.2. Метод Гауса з вибором головного елемента по рядку.

При пошуку головного елемента по рядку місцями міняються не рівняння системи (1.1), як при пошуку по стовпцю, а невідомі xi у всіх рівняннях. Наприклад, на першому кроці методу Гауса серед

коефіцієнтів a11 , a12 ,K, a1n

знайдемо максимальний по абсолютному

значенню коефіцієнт. Нехай це буде коефіцієнт

a1m . Перепишемо

систему, переставивши місцями x1 та xm у всіх рівняннях:

a

x

m

+ a x

2

+K+ a x

+K+ a

x

n

= b

1m

12

11 1

1n

1

a2m xm + a22 x2 +K+ a21 x1 +K+ a2n xn

= b2

(3.3)

LLLLLLLL

.

a

nm

x

m

+ a

n2

x

2

+K+ a

x

+K+ a

nn

x

n

= b

n1 1

n

Від перестановки місцями доданків у рівняннях розв’язок системи не зміниться. На наступному кроці методу Гауса знаходимо максимальний коефіцієнт серед a22(1) , a23(1) ,K, a2(1n) та знову здійснюємо заміну, і т.д.

10

Після завершення зворотного ходу методу Гауса необхідно знову виконати перестановку xi , тобто впорядкувати елементи вектора X у тому порядку, який був на самому початку.

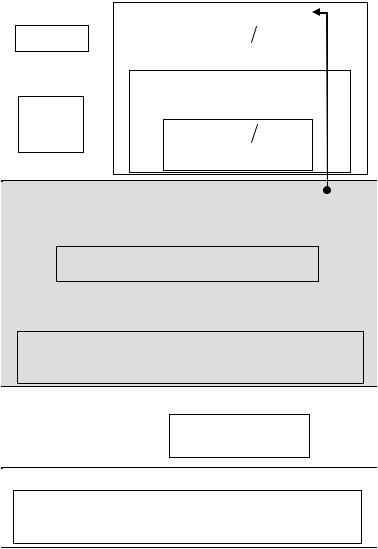
Загальний алгоритм методу Гауса з вибором головного елемента по рядку

для k =

для i =

1, n

1, n

рядкові сортування

inxi

= i

Yk = Pk Vkk

Прямий

для i =

k +1, n

для i, j =

хід:

1, n

Pi = Pi

−Vik Yk

для

j =

Vi, j = Ai, j

k +1,n

P = B

Ckj =Vkj Vkk ;

i

i

Vij =Vij

−Vik Ckj

рядкові сортування

max =

Vkk

, w = k

для l =

k +1, n

якщо max <

Vkl

→ { max =

Vkl

; w =l }

z = inxk ; inxk = inxw ;

inxw = z

для d =

1,n

якщо d < k →{ value =Cdk ; Cdk

=Cdw ; Cdw = value }

інакше

{ value =Vdk ; Vdk =Vdw ; Vdw = value }

Оберне-

для i =

n −1,1

X n

=Yn

ний хід:

n

X i =Yi − ∑Cij X j

j=i+1

для i =

Впорядку-

1, n

z =inxi ; value = Xi ; Xi = X z ;

вання xi

якщо inxi

≠ i →

= value; inxi

X z

=inxz ; inxz = z

11

Опис алгоритму

1.Задаємо початкові значення вектора inxi =[1, 2,K, n] . Цей вектор містить інформацію про переміщення невідомих xi під час вибору головних елементів.

2.Прямий хід методу. Резервуємо (копіюємо) базові матриці A та B

увідповідні матриці V та P . Вхідні матриці A та B нам необхідні

для кінцевої перевірки результату. Протягом виконання алгоритму ми працюємо з копіями вхідних матриць.

3.Далі в трьох циклах виконується перетворення початкової матриці A до трикутного вигляду матриці C та відповідне перетворення

правих частин системи B . Зазначимо, що на кожному кроці першого циклу по змінній k виконуємо процедуру рядкового сортування по головним елементам. Тобто, відшукуємо максимальне значення по модулю головного елемента, а потім міняємо місцями стовпці в матрицях V та P (копії матриць A та B ). Змінна w визначає номер рядка головного елемента, змінна value використовується як проміжна змінна при заміні значень у елементах матриць V та P , а z як проміжна змінна при заміні значень елементів вектора inxi .

4.Обернений хід. Спершу присвоюємо значення для останнього невідомого xn , а потім в циклі відшукуємо усі решта невідомі.

5.На останньому етапі впорядковуємо значення вектора X у тому порядку, який був на самому початку.

6.Для перевірки вірності роботи алгоритму підставляємо наші

знайдені x1 , x2 , ..., xn в систему (1.1). Обчислені ліві частини рівнянь повинні відповідати правим значенням елементів вектора B .

3.3. Метод Гауса з вибором головного елемента по всійматриці.

У схемі повного вибору головний елемент шукається по всій матриці A

a11x1 +a12 x2 +K+a1q xq +K+a1n xn =b1

a x

+a

x

+K+a

x

+K+a x

=b

21 1

22

2

2q q

2n n

2

LLLLLLLL

.

(3.4)

a x

+a

m2

x

+K+

a

mq

x

+K+a

x

=b

m1 1

2

q

mn n

m

LLLLLLLL

a x

+a x

+K+a x

+K+a x

=b

n1 1

n2 2

nq q

nn n

n

12

На першому кроці методу серед елементів aij визначають максимальний по модулю amq . Перше рівняння системи та рівняння з

номером m міняють місцями. Далі переставляють місцями x1

та xq у

всіх рівняннях. Після чого система (3.4) стає такою

xq +am2 x2 +K+am1 x1 +K+amn xn = bm

amq

x

+a

x

+K+a

x

+K+a

x

= b

a

2q

q

22

2

2n

n

21 1

2

LLLLLLLL

(3.5)

a

x

+a x

+K+a x

+K+a

x

= b

.

q

2

n

1q

12

11 1

1n

1

LLLLLLLL

a

x

+a

x

+K+a

x

+K+a

x

= b

nq

q

n2

2

nn

n

n1 1

n

Як бачимо, цей метод об’єднує методи вибору головного елементу по рядку та по стовпцю. Відповідно наш робочий алгоритм методу Гауса з вибором головного елементу по всій матриці буде гібридом двох попередніх методів.

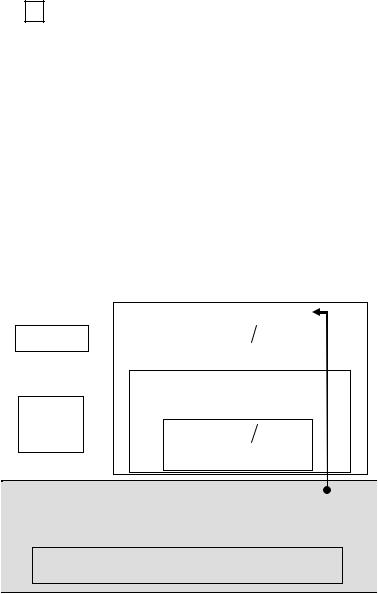
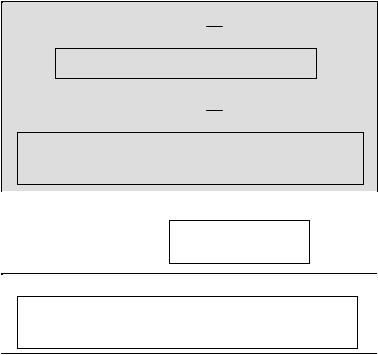
Загальний алгоритм методу Гауса з вибором головного елемента по всій матриці

для i =

для k =

1, n

1, n

матричне сортування

inxi

= i

Yk = Pk Vkk

Прямий

для i =

k +1, n

для i, j =

хід:

1, n

Pi = Pi −Vik Yk

для j =

Vi, j = Ai, j

k +1,n

P = B

Ckj =Vkj Vkk ;

i

i

Vij =Vij −Vik Ckj

матричне сортування

max =

Vkk

; h = k ; w = k

для l, f =

k, n

якщо max <

Vlf

→ { max =

Vlf

; h = l ; w = f }

13

Обернений хід:

Впорядкування xi

value = Pk ; Pk = Ph ; Ph = value

для d =1,n

value =Vkd ; Vkd =Vhd ; Vhd =value

z = inxk ; inxk = inxw ; inxw = z

для d =1,n

якщо d < k →{ value =Cdk ; Cdk =Cdw ; Cdw = value }

інакше

{ value =Vdk ; Vdk =Vdw ; Vdw = value }

для i =

n −1,1

X n =Yn

n

X i =Yi − ∑Cij X j

j=i+1

для i =

1, n

якщо inxi

z =inx

; value = X

; X

= X

;

≠ i →

i

i

i

z

X z = value; inxi =inxz ; inxz

= z

Опис алгоритму

1.Задаємо початкові значення вектора inxi =[1, 2,K, n] . Цей вектор містить інформацію про переміщення невідомих xi під час вибору головних елементів.

2.Прямий хід методу. Резервуємо (копіюємо) базові матриці A та B у відповідні матриці V та P . Вхідні матриці A та B нам необхідні

для кінцевої перевірки результату. Протягом виконання алгоритму ми працюємо з копіями вхідних матриць.

3.Далі в трьох циклах виконується перетворення початкової матриці A до трикутного вигляду матриці C та відповідне перетворення

правих частин системи B . Зазначимо, що на кожному кроці першого циклу по змінній k виконуємо процедуру матричного сортування по головним елементам. Тобто, відшукуємо максимальне значення по модулю головного елемента, а потім міняємо місцями рядки в матрицях V та P (копії матриць A та B ) та здійснюємо заміну стовпців у матриці V , щоб головний елемент

14

вийшов на верхнє зліва місце. Змінна h та w визначають, відповідно, номер стовпця та рядка головного елемента, змінна value використовується як проміжна змінна при заміні значень у елементах матриць V та P , а z як проміжна змінна при заміні значень елементів вектора inxi .

4.Обернений хід. Спершу присвоюємо значення для останнього невідомого xn , а потім в циклі відшукуємо усі решта невідомі.

5.На останньому етапі впорядковуємо значення вектора X у тому порядку, який був на самому початку.

6.Для перевірки вірності роботи алгоритму підставляємо наші знайдені x1 , x2 , ..., xn в систему (1.1). Обчислені ліві частини рівнянь повинні відповідати правим значенням елементів вектора B .

Усхемі повного вибору головного елемента по всій матриці гарантія доброї обумовленості досягається ціною значних затрат на вибір головних елементів. І тому на практиці у більшості випадках перевага віддається все ж таки схемі часткового вибору головного елемента по стовпцю.

4.Застосування методу Гауса дляобчислення визначників матриць

Нехай маємо деяку матрицю
a	a	L	a
11	12		1n
A = a21	a22	L a2n .			(4.1)
L	L L L
	an2
an1		L ann

Розглянемо лінійну систему
	A X = 0 .				(4.2)
При розв’язуванні системи (4.2) методом Гауса (п.2) ми
здійснювали заміну матриці		A	трикутною матрицею		C , що
складалася з елементів зазначених стрічок,
1 c12		c13	K c1n
		(1)	(1)
C = 0	1	c23	K c2n	.	(4.3)
K K K K K
	0	0	K 1
0
					15

У результаті ми отримували еквівалентну систему
	матриці C	C X =0 .	(4.4)
Елементи		послідовно утворювалися	з елементів
матриці A та	подальших	допоміжних матриць A1 ,	A2 , K, An−1 за
допомогою таких елементарних перетворень:

1)ділення на головні елементи a11 , a22(1) , … , ann(n−1) , які передбачалися відмінними від нуля, та

2) віднімання із рядків матриці A та проміжних матриць A1 , A2 , K, An−1 чисел, що пропорційні елементам відповідних

головних стрічок.

При першій операції визначник матриці також ділиться на відповідний головний елемент, при другій – визначник матриці залишається незмінним. Тому

det C =1 =		det A
				.
	a a(1)		Ka(n−1)
11		22	nn
Отже
det A = a a(1) Ka(n−1)					(4.5)
11		22	nn

Як бачимо з виразу (4.5), визначник дорівнює добутку головних елементів для відповідної схеми Гауса. До того ж немає потреби здійснювати обчислення для вектора вільних членів B та операції зворотного ходу – вистачає лише прямого ходу методу Гауса.

Загальний алгоритм обчислення визначника матриці простим методом Гауса

	det =1				для k =		1, n
					det = det Vkk
	для i, j =				для i, j =
Прямий			1, n			k +1,n
хід:	V	= A			Ckj =Vkj Vkk ;
	i, j	i, j
					Vij =Vij −Vik Ckj

Опис алгоритму

1.На початку алгоритму змінній det , що відповідає за значення визначника, присвоюємо одиницю. Копіюємо матрицю A у V .

16

2.Виконуємо спрощений прямий хід методу Гауса (без обчислень для вектора B ). На кожному кроці першого циклу по змінній k помножаємо значення визначника на значення головного елементу.

Зазначимо, що якщо будь-який головний елемент akk(k −1) =0 чи

близький до нуля (тягне за собою зменшення точності обчислень), то необхідно використовувати метод Гауса з вибором головного елемента (повну або часткову схему).

При використанні методу Гауса з вибором головного елемента слід врахувати таку деталь: оскільки величина визначника рівна сумі добутків елементів стовпця (рядка) матриці на

(−1)i+ j A ij ,

де A ij – відповідні мінори (у методі Гауса на кожному кроці прямого

ходу у робочому стовпці усі елементи, за винятком першого верхнього, рівні нулю), то слід у формулі (4.5) врахувати знак для кожного головного елемента, який був переміщений з іншого місця матриці.

Загальний алгоритм обчислення визначника матриці методом Гауса з вибором головного елемента по стовпцю

det =1

для k =

1, n

стовпцеві сортування

det = det (−1)w+k V

для i, j =1, n

Прямий

kk

для i, j

= k +1,n

хід:

Vi, j

= Ai, j

Ckj =Vkj Vkk ;

Vij =Vij

−Vik Ckj

стовпцеві сортування

max =

Vkk

; w = k

для l =

k +1, n

якщо max < Vlk → { max = Vlk ; w =l }

для d =1,n

value =Vkd ; Vkd =Vwd ; Vwd =value

17

Опис алгоритму

1.На початку алгоритму змінній det , що відповідає за значення визначника, присвоюємо одиницю. Копіюємо матрицю A у V .

2.Виконуємо спрощений прямий хід методу Гауса (без обчислень для вектора B ). На кожному кроці першого циклу по змінній k проводимо спочатку стовпцеві сортування для визначення максимального по модулю значення головного елемента та опісля помножаємо значення визначника на значення головного елементу із коефіцієнтом (−1)w+k його місця розташування.

Аналогічно до цього будуються й алгоритми для обчислення визначника матриці на основі методів Гауса з визначенням головного елемента по рядку та по всій матриці. Відрізняються вони лише процедурами сортування.

Загальний алгоритм обчислення визначника матриці методом Гауса з вибором головного елемента по рядку

det =1

для k =

1, n

рядкові сортування

det = det (−1)w+k V

для i, j =1, n

Прямий

kk

для i, j

= k +1,n

хід:

Vi, j = Ai, j

Ckj =Vkj Vkk ;

Vij =Vij

−Vik Ckj

рядкові сортування

max =

Vkk

; w = k

для l =

k +1, n

якщо max <

Vkl

→ { max =

Vkl

; w =l }

для d =

1,n

якщо d < k

→{ value =Cdk ; Cdk =Cdw ; Cdw = value }

інакше

{ value =Vdk ; Vdk

=Vdw ; Vdw = value }

18