Методичка №2

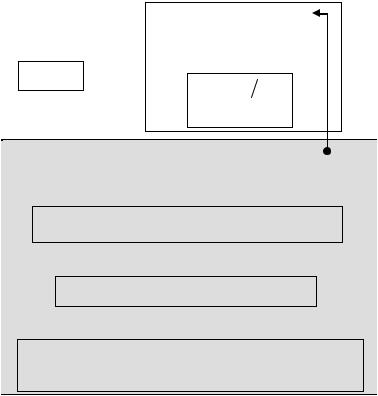
Загальний алгоритм обчислення визначника матриці методом Гауса з вибором головного елемента по всій матриці

det =1

для k =

1, n

матричне сортування

det = det (−1)w+h V

для i, j =1, n

Прямий

kk

для i, j

= k +1,n

хід:

Vi, j = Ai, j

Ckj =Vkj Vkk ;

Vij =Vij

−Vik Ckj

матричне сортування

max =

Vkk

; h = k ; w = k

для l, f =

k, n

якщо max <

Vlf

→ { max =

Vlf

; h = l ; w = f }

для d =

1,n

value =Vkd ; Vkd =Vhd ; Vhd =value

для d =

1,n

якщо d < k

→{ value =Cdk ; Cdk =Cdw ; Cdw = value }

інакше

{ value =Vdk ; Vdk

=Vdw ; Vdw = value }

5. Застосування методу Гауса дляобчислення оберненої матриці

Нехай дано неособливу матрицю
		a	a	L a
		11	12	1n
A = a		= a21	a22	L a2n .		(5.1)
	ij	L	L L L
			an2
		an1		L ann
Для знаходження її оберненої матриці
			A−1	= x		(5.2)
				ij
						19

використаємо основне співвідношення

де E – одинична матриця.

A A−1

= E ,

(5.3)

Множачи матриці A та A−1 ,

будемо мати n

систем рівнянь

відностно n2 невідомих x

ij

∑n

aib xbj = δij

,

i, j =

,

(5.4)

1, n

де

b=1

коли i = j

δij

=

1,

.

коли i ≠

j

0,

Проілюструємо формулу (5.4) на прикладі матриці з n = 3 .

a11

a12

a13

x11

x12

x13

1

0

0

a21

a22

a23

x21

x22

x23

=

0

1

0

0

0

1

a31

a32

a33

x31

x32

x33

A

×

A−1

=

E

Тепер розіб’ємо на три окремі системи рівнянь

a11

a12

a13

x11

1

a11

a12

a13

x12

0

a21

a22

a23

x21

=

0

,

a21

a22

a23

x22

=

1

,

0

0

a31

a32

a33

x31

a31

a32

a33

x32

A

×

X

1

=

E

A

×

X 2 = E2

1

a11

a12

a13

x13

0

a21

a22

a23

x23

=

0

,

1

a31

a32

a33

x33

A

×

X3 = E3

де A –

матриця

коефіцієнтів

системи;

X1 ,

X 2 ,

X 3

–

вектора

невідомих; E1 , E2 , E3

– вектора вільних членів (аналогічно вектору B

системи рівнянь (1.2) ).

20

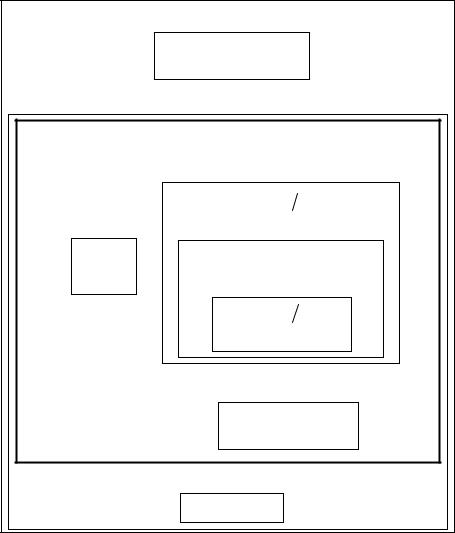
Прямий хід:

Загальний алгоритм обчислення оберненої матриці методом Гауса

для i, j =

1, n

якщо i = j

→ { Eij

=1}

інакше

{ Eij

=0 }

для b =

1,n

Метод Гауса

для k =

1, n

для i, j =

Yk

= Pk Vkk

1, n

для i =

k +1, n

Vi, j = Ai, j

P = P −V Y

Pi = Eib

i

i

ik k

для

j =

k +1,n

Ckj

=Vkj Vkk ;

Vij =Vij

−Vik Ckj

Обернений хід:

		для i =			n −1,1
X n	=Yn				n
		X i =Yi − ∑Cij X j
				j=i+1
		для i =
			1,n
		INVERSi,b = X i
		Опис алгоритму

1.Встановлюємо значення для одиничної матриці E .

2.У верхньому циклі по змінній b здійснюємо пошук n стовпців

оберненої матриці INVERS шляхом розв’язування n систем

21

рівнянь (5.4) методом Гауса. У прямому ході методу Гауса ми замість вектора вільних членів B передаємо методу відповідний стовпець одиничної матриці E . Після закінчення роботи методу Гауса здійснюємо присвоєння обчислених значень елементів вектора невідомих X відповідному стовпцю оберненої матриці

INVERS .

3.Виконуємо перевірку алгоритму. Скалярно помножимо матрицю A на знайдену їй обернену матрицю INVERS . У результаті маємо отримати одиничну матрицю E (в межах похибки обчислень).

Зметою уникнення ситуації, коли головні елементи можуть бути рівними чи близькими нулю необхідно використовувати метод Гауса з вибором головного елемента. У наведеному вище алгоритмі потрібно лише замінити використаний звичайний метод Гауса на метод із повним чи частковим вибором головного елемента (стр. 9, 11, 13).

Єдиною модифікацією для них є лише Pi = Eib на початку прямого ходу.

6. Метод LU-розкладу

Алгоритми цього методу є схожими до методу Гауса. Основна перевага методу LU-факторизації в порівнянні з методом Гауса полягає в більш простому отриманні розв’язку для різних векторів B системи лінійних алгебричних рівнянь (1.1).

У цьому методі матрицю A подають як скалярний добуток двох трикутних матриць L та U

де			A = L U ,
l	0	K 0			1
11
L = l21	l22	K 0		,	U =	0
K K		K K			K
	ln2					0
ln1		K lnn

(6.1)

u	K u
12	1n
1	K u2n .
K K K
0
	K 1

Запишемо систему (1.2) із врахуванням виразу (6.1)
L U X = B .	(6.2)
Введемо допоміжний вектор Y як
U X =Y .	(6.3)

22

Після цього запишемо вираз (6.2) так
L Y = B .	(6.4)

Розв’язок системи (1.2) чи (6.2) відбувається в два етапи: спершу розв’язується система (6.4), а потім (6.3). Така послідовність розв’язування дає перевагу методу (у порівнянні з методом Гауса) при розв’язуванні декілька систем з однаковою матрицею A та різними векторами вільних членів B , оскільки матриці L та U залишаються незмінними.

Розв’язування системи (6.4) складає прямий хід методу, а системи (6.3) – обернений хід.

Розглянемо прямий хід. Завдяки спеціальній формі матриці L вектор Y легко обчислюється. Для цього запишемо вираз (6.4) у виді системи рівнянь

			l11 y1			=b1
			l21 y1 + l22 y2			=b2 .				(6.5)
				KKKKKK
			ln1 y1 +ln2 y2 +K+ lnn yn			=bn
	Узагальнені формули для системи (6.5) є такими
					i−1
	y1 = b1	l1,1	;				для i = 2, n .			(6.6)
				yi = bi	−∑li,m ym li,i
					m=1
	Приоберненомуходівектор X визначаєтьсязсистемирівнянь(6.3)
			x1 +u12 x2 +K+u1n xn			= y1
				x2 +K+u2n xn		= y2 .				(6.7)
				KKKKKK
					xn	= yn

Починаючи з останнього рівняння, можна послідовно знайти елементивектора X . Запишемоузагальненіформулидлясистеми(6.7)

xn = yn ; xi = yi − ∑n ui,m xm для i = n −1,1. (6.8)

m=i+1

LU-розкладматриці A здійснюватимемометодомКраута.

23

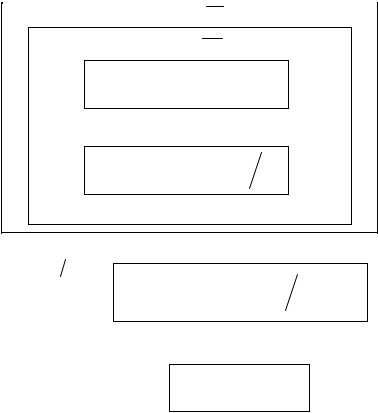
LU-

розклад:

Прямий хід:

Обернений хід:

Загальний алгоритм методу LU-розкладу

для k =1, n

для i = k, n

			k −1
		Li,k = Ai,k −∑Li,mU m,k
			m=1
		для	j =
				k +1, n
		= Ak , j −	k −1
U k , j			∑Lk ,mU m, j Lk ,k
			m=1
		Uk ,k =1
Y1 = B1 L1,1				для i =				2, n
		Yi = Bi			−∑Li,mYm					Li,i
					i−1
					m=1
				для i =			n −1,1
X n =Yn						n
			X i =Yi − ∑Ui,m X m
						m=i+1
Опис алгоритму

1.Виконуємо розклад матриці A на матриці L та U .

2.Прямий хід методу. Обчислюємо перший елемент вектора Y , а потім у циклі відшукуємо усі решта елементи.

3.Обернений хід методу. Спершу присвоюємо значення для останнього невідомого xn , а потім в циклі відшукуємо усі решта невідомі.

4.Для перевірки вірності роботи алгоритму підставляємо наші знайдені x1 , x2 , ..., xn в систему (1.1). Обчислені ліві частини рівнянь повинні відповідати правим значенням елементів вектора B .

24

7. Метод прогону

Метод прогону є простим та ефективним алгоритмом для розв’язування систем лінійних алгебричних рівнянь з трьохдіагональнимиматрицями

b1 x1 +c1 x2

a2 x1 +b2 x2 +c2 x3

a3 x2 +b3 x3 +c3 x4

KKKKKKK

ai xi−1 +bi xi +ci xi+1

KKKKKKK

an−1 xn−2 +bn−1 xn−1 +cn−1 xn an xn−1 + bn xn

Систему (7.1) у загальному випадку записують так:

= d1
= d2
= d3
KK		(7.1)
= di
KK
= dn−1
= dn

a1 =0 ; cn =0 ; ai xi−1 +bi xi + ci xi+1 = di , i =

2, n

(7.2)

Прямий хід прогону (алгоритм прямого ходу методу Гауса). Кожне невідоме xi виражається через xi+1 з допомогою

прогонних коефіцієнтів Ai та Bi

xi = Ai xi+1 + Bi

, i =

1,n

.

(7.3)

Наприклад, з першого рівняння системи (7.1) знайдемо

x1 = −

c1

x2 +

d1

A

= −

c1

b

1

b1

b1

,

звідки

1 .

(7.4)

x

= A x

+ B

B1

=

d1

1

1 2

1

b1

Із другого рівняння системи (7.3) виразимо

x2 через x3 ,

замінюючи x1 формулою (7.3) або (7.4)

a2 x1 +b2 x2 +c2 x3 = a2 (A1 x2 + B1 )+b2 x2 +c2 x3 = d2 .

Звідси знайдемо

x

2

=

d2

−c2 x3 −a2 B1

або

x

2

= A x + B ,

a2 A1 +b2

2

3

2

25

де

A

= −

c2

,

B

=

d2 −a2 B1

.

2

a2 A1 +b2

2

a2 A1

+b2

Приймаючи, що е2 = а2А1 + b2 , запишемо:

A = − c2 ;

B =

d2 −a2 B1

.

2

e2

2

e2

Аналогічно для кожного i -го індексу прогонні коефіцієнти з

рівняння (3) мають вигляд:

di −ai Bi−1

A = − ci

,

B

=

,

(7.5)

i

ei

i

ei

де ei = ai Ai−1 +bi ,

i =

1,n

.

При цьому враховуючи, що a1 = cn = 0 , приймаємо

A0

= 0 ,

B0

= 0 .

(7.6)

У розгорнутому вигляді формула (7.5) буде мати вигляд формули (7.7)

xi−1 = Ai−1 xi + Bi−1

ai xi−1 +bi xi +ci xi+1 = di

ai (Ai−1 xi + Bi−1 )+bi xi +ci xi+1 = di

x

=

di −ci xi+1 −ai Bi−1

= −

ci

x

+

di

−ai Bi−1

= A x

+ B

(7.7)

a A

+b

a A

+b

i

a A

+b

i+1

i i+1

i

i i−1

i

i i−1

i

i

i−1

i

Значення прогонних коефіцієнтів (7.7) можна одержати й таким шляхом. У рівнянні (7.3) понизимо індекс на одиницю та підставимо значення xi−1 в i -те рівняння системи (7.2)

Обернений хід прогону (аналог оберненого ходу методу Гауса). Він полягає в послідовному обчисленні невідомих xi . Спочатку

знаходять xn .

Для

цього

формулу

(7.7)

запишемо

при

i = n

(враховуючи, що cn = 0 )

x

= −

cn

x

n+1

+

dn −an Bn−1

=

dn −an Bn−1

= B .

a

A

+b

n

a A

+b

a A

+b

n

n n−1

n

n n−1

n

n n−1

n

Далі, використовуючи формулу (7.3), знаходимо послідовно усі

невідомі xn−1 , xn−1 , K, x1 .

Для запису коефіцієнтів ai

, bi та прогонних коефіцієнтів

Ai−1 ,

Bi−1 використовується той самий масив.

26

Ініціалізація:

Прямий хід:

Обернений хід:

Вихідні дані:

Загальний алгоритм методу прогону

для i =1, n

Ai+1 = ai ; Bi+1 = bi ; Ci+1 = ci ; Di+1 = di

A1 =0 ; B1 =0

для i = 2,n +1

value = A A

+ B ;

B

=

Di − Ai Bi−1

;

A

=

−Ci

i i−1

i

i

value

i

value

X n+1 = Bn+1

для i =

n,2

Xi = Ai Xi+1

+ Bi

для i =1, n

xi = X i+1

Опис алгоритму

1.На етапі ініціалізації ми копіюємо вхідні дані (вектори a , b , c , d розмірності n ) у вектори методу A , B , C , D з розмірністю n +1. Елементи вхідних векторів розміщуються у векторах методу, починаючи з другої комірки. Це є необхідним, щоб можна було за-

дати значення для початкових коефіцієнтів прогону A1 =0 , B1 =0 . Треба зазначити, що значення коефіцієнтів системи (7.1) a1 = cn = 0 мають бути вже задані у вхідних даних.

2.Прямий хід методу. Обчислюються коефіцієнти прогону A та B . У змінній value обчислюється вираз з їх попередніми значеннями.

3.Обернений хід. Спершу присвоюємо значення для останнього невідомого, а потім у циклі відшукуємо усі решта невідомі.

4.На останньому етапі повертаються значення у вектор x .

5.Для перевірки вірності роботи алгоритму підставляємо наші знайдені x1 , x2 , ..., xn в систему (7.1). Обчислені ліві частини рівнянь повинні відповідати правим значенням елементів вектора d .

27

8. Метод простої ітерації

Трансформуємо систему (1.2) до такого вигляду

X =VX + P ,

(8.1)

де V

–

числова квадратна матриця n -го порядку,

P – вектор вільних

членів.

Це здійснюється

шляхом вираження x1

з першого рівняння

системи (1.1), x2

– з другогорівняння,

xn

– з n -горівняння

x

= v x

2

+ v x

3

+K+ v

x

n

+ p

1

12

13

1n

1

x2

= v21 x1 + v23 x3 +K+ v2n xn + p2

,

(8.2)

LLLLLLLL

x

n

= v

x

+ v

n2

x

2

+K+ v

nn−1

x

n−1

+ p

n

n1 1

де p

=

b

v

= −

aij

, при i ≠ j ;

v

= 0 ,

при i = j . При цьому

i

i

;

aii

ij

aii

ij

вважаємо, що діагональні коефіцієнти aii ≠ 0 ,

i =

1,n

.

Метод простої ітерації полягає в наступному. Вибирається довільне

початкове наближення вектора X = X (0) та будується ітераційна послідовність векторів заформулою

X (k +1) =VX (k ) + P , k = 0,1,2,K

(8.3)

Ітераційний процес триває до тих пір, поки не виконається умова його збіжності

	X (k +1) − X (k )	100% < ε ,	(8.4)
	X (k +1)

де ε – заданапохибка збіжності ітераційного процесуу відсотках.

Умова збіжності: якщо сума модулів елементів рядків або стовпців матриці V є меншою за 1, то процес ітерації для даної системи збігається до єдиного розв’язку, незалежно від вибору вектора початкових наближень.

Ця умова збіжності вважається достатньою, але не необхідною. Тобто, якщо умова виконується, то процес буде збіжним. Коли ж умова не виконується, тоце щене означає, щопроцесбудерозбіжним.

28