Методичка №2

Міністерство освіти та науки України Національний університет “Львівська політехніка”

Реєстр. № 2409

від 10.10.2007

ПРЯМІ ТА ІТЕРАЦІЙНІ МЕТОДИ РОЗВ’ЯЗУВАННЯ СИСТЕМ ЛІНІЙНИХ АЛГЕБРИЧНИХ РІВНЯНЬ

Інструкція до лабораторної роботи № 2

з курсу “Комп’ютерні методи дослідження систем керування”

для студентів базового напрямку 6.0914 “Комп’ютеризовані системи, автоматика і управління” та базового напрямку 050201 “Системна інженерія”

Затверджено на засіданні кафедри

“Комп’ютеризовані системи автоматики” Протокол № 2 від 03.10.2007

Львів 2007

Прямі та ітераційні методи розв’язування систем лінійних алгебричних рівнянь: Інструкція до лабораторної роботи № 2 з курсу “Комп’ютерні методи дослідження систем керування” для студентів базового напрямку 6.0914 “Комп’ютеризовані системи, автоматика і управління” та базового напрямку 050201 “Системна інженерія” / Укл.: У.Ю. Дзелендзяк, А.Г. Павельчак, В.В. Самотий – Львів: НУЛП, 2007.- 36 с.

Укладачі: У.Ю. Дзелендзяк, к.т.н., доцент А.Г. Павельчак, асистент В.В. Самотий, д.т.н., професор

Відповідальний за випуск:

А.Й. Наконечний, д.т.н., професор

Рецензент: З.Р. Мичуда, д.т.н., професор

Мета роботи: вивчити найпоширеніші прямі та ітераційні методи розв’язування систем лінійних алгебричних рівнянь та способи їх застосування для обчислення визначників і обертання матриць.

1. Загальна характеристика методів розв’язування систем лінійних алгебричних рівнянь

До числових методів лінійної алгебри відносяться числові методи розв’язування систем лінійних алгебричних рівнянь, обертання матриць, обчислення визначників та знаходження власних чисел і власних векторів матриць. У цій лабораторній роботі ми детально розглянемо першу задачу та побічно вирішимо другу та третю.

1.1. Системи лінійних рівнянь.

Лінійні системи в обчисленнях відіграють дуже значну роль, оскільки до них може бути приведений наближений розв’язок широкого кола задач. Основними джерелами виникнення систем лінійних алгебричних рівнянь є теорія електричних кіл, рівняння балансів та збереження в механіці, гідравліці тощо.

Система n лінійних рівнянь з n невідомими може бути представлена в такому вигляді:

a x

+a x

2

+K+a

x

n

= b

11 1

12

1n

1

a21 x1 +a22 x2 +K+a2n xn

= b2

,

(1.1)

LLLLLLLL

a

x

+a

n2

x

2

+K+a

nn

x

n

= b

n1 1

n

або в матричній формі

A X = B ,

(1.2)

де A – матриця коефіцієнтів системи (1.1),

X – вектор невідомих, B

– вектор вільних членів, які, відповідно, приймають такі значення

		a
		11
A = a		= a21
	ij	L
		an1

a	L a
12	1n
a22	L a2n		,
L L L
an2
	L ann

		x
		1
X = x		= x2		,
	j	L
		xn

	b1
B =b	= b2	.
i	L
	bn

У числових алгоритмах вираз (1.2) переважно записують так

∑n aij x j =bi , i =1, n . (1.3)

j=1

1

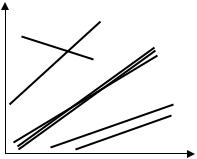
Відомо, що якщо визначник матриці A рівний нулю, тобто det A = 0 , то система лінійних рівнянь або не має розв’язку, або має їх безмежну кількість. Якщо ж det A ≠ 0 , тоді система має розв’язок, та до того ж єдиний. У подальшому ми будемо розглядати лише останній випадок.

y

det A ≠ 0

det A ≈ 0

det A = 0 x

Рис.1.

1.2. Види матриць.

Всі ці випадки є добре геометрично проілюстровані на системі двох рівнянь (рис.1). Кожному рівнянню відповідає пряма в площині x, y, а крапка перетину цих прямих є розв’язком системи. Якщо det A = 0 , то нахили прямих рівні, і вони або паралельні, або співпадають. В іншому випадку прямі мають єдину крапку перетину.

Ефективність обчислень у лінійній алгебрі часто залежить від вміння використовувати спеціальну структуру та властивості задіяних матриць.

а) Матриці, більшість елементів яких нулі, називають розрідженими. Одне із визначень розрідженої матриці таке: матриця

A розміром n ×n вважається розрідженою,	якщо число її ненульових
елементів ~ n1+γ (γ ≤ 0,5) . Наприклад, при	n =103 та γ = 0,5 число

ненульових елементів 31622 (загальне число елементів 106 ). Розрідженість матриць є цінною властивістю, оскільки об’єм інформації, який необхідно обробляти та зберігати в пам’яті обчислювальної машини, для таких матриць навіть дуже значного розміру може виявитися не надто великим. Одним з основних джерел розріджених матриць є математичні моделі технічних пристроїв, що складаються із великої кількості елементів з локальними зв’язками. Найпростіший приклад – великі електричні кола. Інше важливе джерело розрідженості – метод кінцевих різниць та метод кінцевих елементів, що використовуються для розв’язування рівнянь математичної фізики.

б) Стрічкові матриці. Багато задач приводять до матриць, які не тільки розріджені, але й мають стрічкову структуру ненульових елементів. Матриця A називається стрічковою з напівшириною

2

стрічки рівній l , якщо

ai j = 0

для

i − j

> l .

Усі

s

ненульові

елементи

такої матриці розташовані

на

s = 2l

+1найближчих до головної діагоналях матриці;

число

s

прийнято

називати

шириною

стрічки.

Схематично стрічкова

матриця

представлена

на

рис. 2. Частковим випадком стрічкової матриці при

Рис. 2.

s = 3

є трьохдіагональна матриця, яка виникає при

розв’язуванні систем лінійних алгебричних рівнянь у задачах

побудови

інтерполяційних

сплайнів,

різницевих

методах

розв’язування крайових задач для диференціальних рівнянь

a11

a12

0

0

L 0

0

0

a21

a22

a23

0

L 0

0

0

0

a32

a33

a34

L 0

0

0

L L L L L

L

L

L

.

(1.4)

0

0

0

0

L

a

a

a

n−1,n−2

n−1,n−1

n−1,n

0

0

0

0

L 0

an,n−1

an,n

в) Важливу роль у числовому аналізі відіграють трикутні матриці. Квадратна матриця A називається нижньою трикутною, якщо всі її елементи, що розміщені вище головної діагоналі, рівні нулю ( ai j = 0 для i < j ). Якщо ж рівні нулю всі елементи матриці, що

розміщені нижче головної діагоналі ( ai j = 0 для i > j ), то вона

називається верхньою трикутною.

Нижня та верхня трикутні матриці мають відповідно такий вигляд:

a	0	0	L	0			a		a	a	L a
11								11	12	13	1n
a21	a22	0	L	0				0	a22	a23	L a2n
a31	a32	a33	L	0		,		0	0	a33	L a3n		. (1.5)
L L L L L							L L L L L
	an2	an3						0	0	0
an1			L ann								L ann

Трикутні матриці володіють рядом чудових властивостей. Наприклад, для таких матриць визначник легко обчислюється за формулою

det A = a11a22 a33 Kann .	(1.6)
	3

1.3. Методи розв’язування.

Одним з тривіальних методів розв’язування системи лінійних алгебричних рівнянь є метод з використанням зворотної матриці.

Насправді,	при умові det A ≠ 0 існує	зворотна матриця	A−1 .
Домножуючи обидві частини рівняння (1.2) зліва на матрицю			A−1 ,
отримуємо
або	A−1 A X = A−1 B
	X = A−1 B .
			(1.7)
Пошук оберненої матриці здійснюється за формулами Крамера.
Однак для	великих розмірів матриці A	такий підхід є достатньо

громіздкою операцією і на практиці не використовується. Натомість є розроблено ряд значно ефективніших та простіших методів.

Методи розв’язування систем лінійних алгебричних рівнянь в основному поділяють на дві групи:

а) точні або прямі методи – алгоритми, що дають можливість точно (без округлень) розв’язати систему за скінчене число арифметичних дій (метод Гауса, метод LU-розкладу, метод прогону).

б) ітераційні методи, які дають можливість отримати корені системи із заданою точністю шляхом збіжних нескінченних процесів (метод простої ітерації, метод Зейделя, метод релаксації).

Внаслідок неминучих заокруглень результати навіть точних методів є наближеними, до того ж оцінити похибки коренів у загальному випадку є не просто. При використанні ітераційних процесів, крім цього, добавляється ще й похибка методу. Зазначимо, що ефективне використання ітераційних методів суттєво залежить від вдалого вибору початкового наближення та швидкості збіжності процесу.

Для систем невеликого порядку n < 200 застосовують, як правило, тільки прямі методи. Ітераційні методи є вигідними для систем спеціального виду зі слабо заповненою матрицею дуже

високого порядку n ≈103 ÷106 . Метод прогону використовують для розв’язування важливого класу спеціальних систем лінійних рівнянь з трьохдіагональною матрицею, що виникають у ряді задач.

2. Метод Гауса

Суть методу полягає в послідовному виключенню невідомих, у результаті чого дана система рівнянь перетворюється до еквівалентної

4

системи з верхньою трикутною матрицею, розв’язування якої не представляє труднощів. Розглянемо цей метод детально.

Метод Гауса для розв’язування

системи

(1.1) полягає у

послідовному вилученні невідомих x1 , x2 ,

...,

xn−1 з цієї системи.

Нехай a11 ≠ 0 (головний елемент). Поділивши перше рівняння на

a11 , отримаємо

x1 + c12 x2 + ... + c1n xn = y1 ,

(2.1)

де c1 j = a1 j / a11 ; j =

,

y1 =b1 / a11 .

2, n

Розглянемо тепер рівняння системи (1.1), що залишилися

a

x

+ a

x

+K+ a

2n

x

n

=b

21 1

22

2

2

(2.2)

LLLLLLLL

.

a

x

+ a

n2

x

2

+K+ a

nn

x

n

=b

n1 1

n

Почергово,

помножимо

(2.1) на ai1 та отримане

рівняння

віднімемо з відповідного і-го ( i =

) рівняння системи (2.2).

2,

n

У результаті отримаємо таку систему рівнянь

x1 +c12 x2 + ...

+c1 j xj + ... +c1n xn

= y1

(1)

+ ...

(1)

xj

(1)

(1)

a22 x2

+a2 j

+ ... +a2n xn

=b2

(2.3)

........................................

.

a(1) x

2

+ ...

+a(1) x

j

+ ... +a(1) x

n

=b(1)

n2

nj

nn

n

де

a(1)

= a

−c

a

, b(1)

= b − y a

,

i, j =

.

ij

i1

i1

2,n

ij

1 j

i

i

1

У системі (2.3) невідоме x1 міститься лише у першому рівнянні,

тому у подальшому достатньо мати справу з скороченою системою рівнянь:

(1)

x2

(1)

(1)

(1)

a22

+ ...

+a2 j xj

+ ...

+a2m xm

=b2

(2.4)

..........

..........

..........

..........

.

a(1) x

2

+ ...

+a

(1) x

j ...

+

+a

(1) x

n

=b(1)

n2

nj

nn

n

У такий спосіб ми здійснили перший крок методу Гауса. Коли a22(1) ≠ 0 (головний елемент другого кроку), то з системи (2.4) аналогічно можна вилучити невідоме x2 і отримати систему, еквівалентну (1.1), з матрицею такої структури:

5

1		×	×	...	×
	0	1	×	...	×
	0	0	×	...	×		,	(2.5)
...		...	...	...	...
	0	0	×	...	×

де хрестиками позначені ненульові елементи. При цьому перше рівняння системи (2.3) залишається без змін.

Вилучаючи таким ж чином невідомі x3 , x4 , ...., приходимо до системи рівнянь виду

x1 +c12 x2 + ... +c1,n−1 xn−1 +c1n xn = y1

x2 + ... +c2,n−1 xn−1 +c2n xn = y2 ,

...............................

xn = yn

що еквівалентна початковій системі (1.1). Матриця цієї системи є верхньою трикутною

	1	c12 ...	c1,n−1	c1n
	0	1 ...	c2,n−1	c2n
C = ... ... ... ...				...	.
	0	0 ...	1	cn−1,n
	0	0 ...	0	1

xn−1 , остаточно

(2.6)

(2.7)

Побудова системи (2.6) складає прямий хід методу Гауса. Зворотний хід полягає у відшукуванні невідомих x1 , ..., xn з систе-

ми (2.6), починаючи з xn до x1 . Це здійснити просто, оскільки матриця має трикутний вигляд. Дійсно,

xn = yn ,	xn−1 = yn−1 −cn−1,n xn , ...
Загальні форми зворотного ходу мають вигляд
xn = yn ,	xi = yi − ∑n	cij x j , i =		.	(11)
			n −1, 1
	j=i+1

При реалізації на персональному комп’ютерові прямого ходу методу Гауса немає необхідності діяти зі змінними x1, x2 , ..., xn .

Досить вказати алгоритм, за яким початкова матриця А перетворюється до трикутного вигляду (2.7), та вказати відповідне перетворення правих частин системи.

6

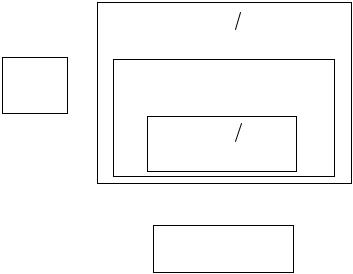
Загальний алгоритм методу Гауса

для k =

1, n

для i, j =

Yk

= Pk

Vkk

1, n

для i =

Прямий

k +1, n

Vi, j

= Ai, j

P = P −V Y

хід:

Pi

= Bi

i

i

ik k

для

j =

k +1,n

Ckj

=Vkj

Vkk ;

Vij =Vij −Vik Ckj

Оберне-

для i =

n −1,1

ний хід:

X n

=Yn

n

X i =Yi − ∑Cij X j

j=i+1

Опис алгоритму

1.Прямий хід методу. Резервуємо (копіюємо) базові матриці A та B у відповідні матриці V та P . Вхідні матриці A та B нам необхідні

для кінцевої перевірки результату. Протягом виконання алгоритму ми працюємо з копіями вхідних матриць.

2.Далі в трьох циклах виконується перетворення початкової матриці A до трикутного вигляду матриці C та відповідне перетворення

правих частин системи B .

3.Обернений хід. Спершу присвоюємо значення для останнього невідомого xn , а потім в циклі відшукуємо усі решта невідомі.

4.Для перевірки вірності роботи алгоритму підставляємо наші знайдені x1 , x2 , ..., xn в систему (1.1). Обчислені ліві частини рівнянь повинні відповідати правим значенням елементів вектора B .

7

3.Метод Гауса з вибором головного елемента

Уметоді Гауса при обчисленні елементів матриці C вимагається ділення на головні елементи a11 , a22(1) , … , ann(n−1) . Якщо ж

один з головних елементів рівний нулю, то схему єдиного ділення не можливо реалізувати. І навіть, коли усі головні елементи відмінні від нуля, але серед них є близькі до нуля, то тоді похибки суттєво зростають і не є контрольованими.

3.1. Метод Гауса з вибором головного елемента по стовпцю.

Для того, щоб уникнути ситуації коли головні елементи є рівними або близькими до нуля, здійснюють перестановку рівнянь у системі (1.1) так, щоб на місці головного елемента опинився елемент з найбільшим по модулю значенням. Тобто, на кожному k -му кроці методу Гауса переставляють стрічки з номерами k, k +1,K, n таким

чином, щоб на місці kk опинився елемент amk(k −1) , найбільший серед

усіх у k -му стовці при m > k . При цьому, звичайно, переставляють і елементи вектора B .

Наприклад, якщо на першому кроці найбільшим елементом у

першому стовпці

виявиться

елемент

am1 ,

то

після

перестановки

місцями першого та m -го рівнянь система (1.1) буде такою

am1 x1 +am2 x2 +K+amn xn =bm

a x

+a

22

x

+K+a

2n

x

= b

21 1

2

n

2

LLLLLLLL

(3.1)

a x

+a x

+K+a x

= b

.

2

n

11 1

12

1n

1

LLLLLLLL

a x

+a

x

+K+a

x

=b

n2

2

nn

n1 1

n

n

Аналогічно здійснюється й на k -му кроці методу Гауса

x

+c x

+ K

+c

x

+ K + c

x

n

= y

1

12 2

1k

k

1n

1

x2 + K +c2k xk +K+ c2n xn = y2

KKKKKK

amk(k −1) xk + K +amn(k −1) xn

= bm(k −1)

(3.2)

KKKKKK

.

a

(k −1) x

+ K +a(k −1) x

= b

(k −1)

kk

k

kn

n

k

KKKKKK

a

(k −1) x

k

+ K +a(k −1) x

n

= b

(k −1)

nk

nn

n

8