МААТЛОГИКА

xy¹ _ x¹y¹ _ xy¹ _ xy, звiдки видно, що ДДНФ дано¨ формули ма¹ чотири доданки, тобто

вона ¹ тавтологiя. n Аналогiчно, ДКНФ протирiччя, тобто тотожно хибно¨ формули, мiстить точно 2

множникiв, де n число всiх змiнних дано¨ формули.

3. Виника¹ природне питання про те, чи можна кожну булеву функцiю зобразити формулою алгебри висловлень. Позитивна вiдповiдь на це питання виплива¹ з наступних двох теорем.

Теорема 9. Кожну булеву функцiю f(x1; x2; : : : ; xn) можна зобразити наступною формулою логiки висловлень:

	(1;:::;1)
f(x1; x2; : : : ; xn) =	f(a1; a2; : : : ; an)x1a1 x2a2 : : : xnan ;	(1.3.3)
	~a=(0;:::;0)

äå ~a = (a1; a2; : : : ; an), ai 2 f0; 1g, x0i = x¹i, x1i = xi для кожного i = 1; 2; : : : ; n.

Доведення. Покажемо, що лiва i права частини спiввiдношення (1.3.3) спiвпадають. Нехай ~a = (a1; a2; : : : ; an) ¹ довiльний двiйковий набiр. Пiдставляючи його

в (1.3.3) в лiвiй частинi будемо мати f(a1; a2; : : : ; an), а в правiй отрима¹мо:

(1;:::;1)

f(a1; a2; : : : ; an)aa11 aa22 : : : aann = f(a1; a2; : : : ; an)aa11 aa22 : : : aann = f(a1; a2; : : : ; an);

~a=(0;:::;0)
îñêiëüêè xiai = 1 ëèøå ïðè xi = ai.	¤

Íàñëiäîê 3. Кожна булева функцiя, яка тотожно не дорiвню¹ нулевi, може бути ¹диним чином зображена в ДДНФ.

Теорема 10. Кожну булеву функцiю f(x1; x2; : : : ; xn) можна зобразити наступною формулою логiки висловлень:

f(x1

; x2

; : : : ; xn) = ~a=(0;:::;0)

³f(a1; a2; : : : ; an) _ x1a¹1 _ x2a¹2

_ : : : _ xna¹n ´;

(1.3.4)

(1;:::;1)

^

äå ~a = (a1; a2; : : : ; an), ai 2 f0; 1g, xi0 = x¹i, xi1 = xi для кожного i = 1; 2; : : : ; n.

Доведення. За законом подвiйного заперечення ма¹мо

(1.3.5)

f(x1; x2; : : : ; xn) = f(x1; x2; : : : ; xn);

а за теоремою 9 можемо записати рiвнiсть

(1;:::;1)

x1a1 x2a2 : : : xnan :

(1.3.6)

f(x1; x2; : : : ; xn) =

f(a1; a2; : : : ; an)

~a=(0;:::;0)

21

Пiдставляючи (1.3.6) в (1.3.5) i застосовуючи закон де Моргана ми отрима¹мо:

		(1;:::;1)
								x1a1 x2a2 : : : xnan =
f(x1; x2; : : : ; xn) =			f(a1; a2; : : : ; an)
		~a=(0;:::;0)
(1;:::;1)	³f(a1; a2									´ =
^		; : : : ; an) _			_		_ : : : _
= ~a=(0;:::;0)				x1a1		x2a2
									xnan
= ~a=(0;:::;0)	³f(a1; a2	; : : : ; an) _ x1a¹1			_ x2a¹2		_ : : : _ xna¹n ´;
(1;:::;1)
^

îñêiëüêè xa1i = xai¹i . ¤

Наслiдок 4. Кожна булева функцiя, яка тотожно не дорiвню¹ одиницi, може бути ¹диним чином зображена в ДКНФ.

Приклад 4. Знайти ДДНФ i ДКНФ для булево¨ функцi¨ f(x; y; z), яка задана такою таблицею iстинностi:

x	y	z		f(x; y; z)
0	0	0		0
1	0	0		1
0	1	0		1
1	1	0		0
0	0	1		0
1	0	1		1
0	1	1		0
1	1	1		0

Спочатку знайдемо ДДНФ для дано¨ функцi¨. Згiдно теореми 9 вiдмiтимо рядки, в яких функцiя прийма¹ значення 1. Кожнiй такiй одиницi вiдповiда¹ певний

двiйковий набiр. Це будуть такi набори: (1; 0; 0), (0; 1; 0), (1; 0; 1). Кожному такому двiйковому набору, як вiдомо,

вiдповiда¹ конституента одиницi, а саме: xy¹z¹, xy¹ z¹, xyz¹ . Îòæå,

ДДНФ для дано¨ функцi¨ ¹ диз'юнкцiя цих конституент одиницi, тобто

f(x; y; z) = xy¹z¹ _ xy¹ z¹ _ xyz:¹

Щоб знайти ДКНФ для вказано¨ булево¨ функцi¨, треба вiдмiтити рядки, в яких значення функцi¨ дорiвню¹ 0. Таких рядкiв п'ять. Далi необхiдно вiдмiтити в цих

рядках двiйковi набори: (0; 0; 0), (1; 1; 0), (0; 0; 1), (0; 1; 1), (1; 1; 1). Пiсля цього для кожного такого двiйкового набору записати вiдповiдну конституенту нуля: x _ y _ z,

x¹ _ y¹ _ z, x _ y _ z¹, x _ y¹ _ z¹, x¹ _ y¹ _ z¹. За теоремою 10 дана функцiя ¹ кон'юнкцiя останнiх конституент нуля, тобто

f(x; y; z) = (x _ y _ z)(¹x _ y¹ _ z)(x _ y _ z¹)(x _ y¹ _ z¹)(¹x _ y¹ _ z¹):

4. Ïiä релейно-контактною схемою розумiють пристрiй, який склада¹ться з провiдникiв i двопозицiйних контактiв. Двопозицiйний контакт це фiзичне тiло, яке може перебувати лише в двох станах ввiмкнено або вимкнуто , якi будемо позначати через 1 i 0 вiдповiдно. Контакти ми позначатимемо малими латинськими

лiтерами.

Мiж собою контакти можуть з'¹днуватись послiдовно i паралельно. При послiдовному з'¹днаннi контактiв сигнал через з'¹днання проходить тодi i тiльки тодi, коли вiн проходить через кожний контакт. При паралельному ж з'¹днаннi контактiв

22

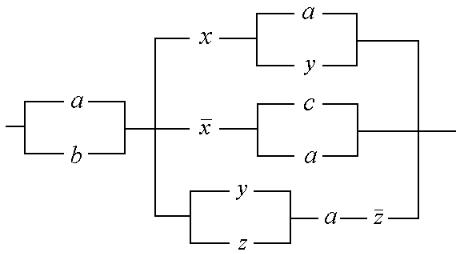
сигнал проходить тодi i тiльки тодi, коли ввiмкнено хоча б один iз контактiв. Таким чином, послiдовне з'¹днання контактiв вiдповiда¹ кон'юнкцi¨ двох логiчних змiнних, а паралельне диз'юнкцi¨. Отже, послiдовне з'¹днання контактiв a i b ми позначатимемо

через ab, а паралельне через a_b. Далi, через a¹ будемо позначати такий контакт, який проводить сигнал тодi i тiльки тодi, коли контакт a його не проводить. Таким чином,

будь-яка булева функцiя може бути реалiзована за допомогою релейно-контактно¨
схеми, оскiльки ¨¨ можна зобразити формулою алгебри висловлень, наприклад, ДДНФ
або ДКНФ, в яких використовуються лише три логiчних операцi¨ кон'юнкцiя,
диз'юнкцiя i заперечення. Так булева функцiя, яка визнача¹ться формулою логiки
висловлень	(a _ b)³x(a _ y) _ x¹(c _ a) _ (y _ z)az¹´;

зображу¹ться наступною релейно-контактною схемою:

23

1.4 Повнi системи булевих функцiй. Алгебра Жегалкiна

Повнi системи булевих функцiй. Теорема про число повних бiнарних логiчних операцiй. Алгебра Жегалкiна. Полiном Жегалкiна. Теорема про зображення булево¨ функцi¨ полiномом Жегалкiна

1. Система булевих функцiй ff1; f2; : : : ; fng назива¹ться повною, якщо довiльна

булева функцiя може бути подана за допомогою перейменування аргументiв i суперпозицi¨ функцiй f1; f2; : : : ; fn, взятих довiльне скiнченне число разiв. Наприклад,

система функцiй f»; ^; _g ¹ повною, оскiльки, як вiдомо з попередньо¨ лекцi¨, кожна

булева функцiя може бути подана ДДНФ або ДКНФ. Популярно означення повноти можна дати таким чином: множина логiчних операцiй © назива¹ться повною, якщо

кожна булева функцiя може бути задана формулою, яка записана за допомогою лише операцiй з ©. Як приклад неповно¨ системи можна навести систему, яка склада¹ться

з однi¹¨ операцi¨ заперечення, тобто ». Це поясню¹ться тим, що за допомогою одного

заперечення можна побудувати лише двi функцi¨ логiчну змiнну та ¨¨ заперечення. Чи iснують крiм f»; ^; _g iншi повнi системи булевих функцiй? Вiдповiдь на це да¹ться

у наступнiй теоремi.

Теорема 11. Системи логiчних операцiй f»; ^g, f»; _g, f j g, f # g (див. стор. 8) ¹ повними.

Доведення. Îñêiëüêè f»; ^; _g ¹ повна система логiчних операцiй i мають мiсце

рiвностi:
	x _ y = x ^ y;			x ^ y = x _ y;
	x¹ = x j x;			x _ y = (x j x)j(y j y);
	x¹ = x # x;			x ^ y = (x # x) # (y # y);

то очевидно наведенi системи операцiй будуть повними.8 ¤

2. З теореми 11 виплива¹, що за допомогою лише однi¹¨ операцi¨ штриха Шеффера або лише однi¹¨ стрiлки Пiрса можна зобразити формулою довiльну булеву функцiю. Виника¹ питання про число булевих функцiй, якi мають подiбну властивiсть. Такi булевi функцi¨ ми надалi будемо називати повними. У випадку бiнарних логiчних операцiй ма¹ мiсце така теорема:

Теорема 12. ™диними бiнарними повними логiчними операцiями ¹ штрих Шеффера i стрiлка Пiрса.

Доведення. Припустимо, що бiнарна логiчна операцiя h(x; y) ¹ повною. Як би h(1; 1) = 1, то довiльна булева функцiя, яку можна зобразити за допомогою лише операцi¨ h(x; y), приймала би значення 1, коли всi ¨¨ аргументи приймали б значення 1. Але ж тодi функцiя x¹ не могла б бути виражена через h(x; y). Îòæå, h(1; 1) = 0. Аналогiчними мiркуваннями ми доводимо, що h(0; 0) = 1. Îòæå, ìè ìà¹ìî:

x	y		h(x; y)
1	1		0
0	1
1	0
0	0		1

Залишаються незаповненими другий i третiй рядки. Для них можливi такi випадки:

à)	0		1		0		0
	0	;	á) 1	;	â) 1	;	ã) 0 .

8 Доведiть, що мають мiсце рiвностi: x ^ y = (x j y)j(x j y), x _ y = (x # y) # (x # y).

24

закон зведення подiбних членiв;

iдемпотентнiсть кон'юнкцi¨;

закон дистрибутивностi;

комутативнiсть суми по модулю 2;

комутативнiсть кон'юнкцi¨;

асоцiативнiсть кон'юнкцi¨;

Випадок а) визнача¹ стрiлку Пiрса, б) штрих Шеффера, в) заперечення y, тобто y¹, г) заперечення x, тобто x¹. Однак, заперечення не ¹ повною булевою операцi¹ю, тому залишаються лише пункти а) i б). ¤

3. Нехай F ¹ множина всiх булевих функцiй. На множинi F можна також розглядати

логiчнi операцi¨, якi для булевих функцiй вводяться таким чином. Нехай f(x1; : : : ; xn) i

g(y1; : : : ; ym) ¹ деякi булевi функцi¨, > деяка логiчна операцiя. Тодi через f>g будемо

позначати булеву функцiю, множиною аргументiв яко¨ ¹ об'¹днання аргументiв даних функцiй, а значення функцi¨ для цих аргументiв визнача¹ться згiдно рiвностi:

df

(f > g)(x1; : : : ; ym) = f(x1; : : : ; xn)> g(y1; : : : ; ym):

Наприклад, кон'юнкцiя функцiй f(x; y; z) i g(y; u; z; v) ¹ функцiя виду (f ^g)(x; y; z; u; v), значення яко¨ визначаються згiдно рiвностi:

(f ^ g)(x; y; z; u; v) = f(x; y; z) ^ g(y; u; z; v):

Аналогiчним чином можна визначити довiльнi логiчнi операцi¨ для булевих функцiй. Алгеброю Жегалкiна ми будемо називати алгебру виду (©; ^; ©), äå © = F [f0; 1g

множина всiх булевих функцiй, доповнена константами 0 i 1, ^ операцiя кон'юнкцi¨, © сума по модулю 2. За допомогою таблиць iстинностi легко доводиться така теорема:

Теорема 13. В алгебрi Жегалкiна виконуються такi спiввiдношення:

1. (xy)z = x(yz)

2. (x © y) © z = x © (y © z) асоцiативнiсть суми по модулю 2;

3. xy = yx

4. x © y = y © x

5. xx = x

6. x © x = 0

7. x(y © z) = xy © xz

8. x ¢ 1 = x, x ¢ 0 = 0, x © 0 = x дi¨ з константами.

Нехай задана алгебра Жегалкiна. Кон'юнкцiя довiльного скiнченного числа попарно рiзних логiчних змiнних назива¹ться одночленом. Наприклад, 1, 0, x, y, xy, xyz, xu.

Далi, сума по модулю 2 скiнченного числа попарно рiзних одночленiв назива¹ться полiномом Жегалкiна. Наприклад, xz ©xy ©x ©z ©1, xyzu ©xy ©z. Сума по модулю 2

скiнченного числа попарно рiзних конституент одиницi над деякою множиною логiчних змiнних назива¹ться досконалою бiсумарною нормальною формою (скорочено ДБНФ). Наприклад, xyz¹©xy¹z¹©xyz ©x¹y¹z¹ ДБНФ. Враховуючи, що x ©0 = x _0, викону¹ться

така теорема:

25

Теорема 14. Кожна булева функцiя, яка тотожно не дорiвню¹ нулевi, може бути ¹диним чином зображена ДБНФ.

Доведення проводиться так, як i для ДДНФ, тому ми його не наводимо. Вiдмiтимо лише, що враховуючи той факт, що конституента одиницi прийма¹ значення 1 òiëüêè

на ¹динному двiйковому наборi, який ¨й вiдповiда¹, а також, що 1 © 0 = 1 _ 0, робимо висновок, що для отримання ДБНФ достатньо в ДДНФ замiнити всi символи операцi¨ _

на символ ©. Наприклад, якщо f(x; y; z) = xyz¹_xy¹z¹_xy¹ z¹, òî f(x; y; z) = xyz¹©xy¹z¹©xy¹ z¹.

4. ДБНФ да¹ нам можливiсть записувати формули у виглядi полiнома Жегалкiна. Наприклад, нехай потрiбно записати диз'юнкцiю x_y полiномом Жегалкiна. Запишемо

спочатку дану диз'юнкцiю в ДДНФ, тобто x _y = xy _xy¹_xy¹ . Тодi ДБНФ ма¹ вигляд: x _ y = xy © xy¹ © xy¹ . Îñêiëüêè x¹ = x © 1, òî

x _ y = xy © x(y © 1) © (x © 1)y = xy © xy © x © xy © y = xy © x © y:

Îòæå, xy © x © y полiном Жегалкiна для x _ y. Виника¹ питання: "Скiльки ма¹

булева функцiя рiзних полiномiв Жегалкiна, що ¨¨ зображують?"Вiдповiдь да¹ться у наступнiй теоремi:

Теорема 15. Кожна булева функцiя може бути ¹диним чином зображена полiномом Жегалкiна.

Доведення. Нехай f(x1; : : : ; xn) ¹ довiльна булева функцiя. Оскiльки константи 0 i 1 самi по собi ¹ полiномами Жегалкiна, то ми можемо обмежитись випадком, коли

f(x1; : : : ; xn) 6´0. Зобразимо цю функцiю в ДБНФ, далi в цiй формi замiнимо вирази типу x¹ íà x © 1, пiсля чого, користуючись законами теореми 14, зводимо формулу до

полiнома Жегалкiна.

Доведемо його ¹диннiсть. Нехай iсну¹ два полiноми ' i Ã, якi зображують одну i ту

ж функцiю f(x1; : : : ; xn). Îñêiëüêè ' i à рiзнi полiноми, то в одному з них знайдеться

такий одночлен, якого нема¹ в другому. Виберемо з таких одночленiв той, який ма¹ найменшу кiлькiсть змiнних. Таким чином, всi одночлени з меншим числом змiнних, присутнi в обох полiномах. Нехай вибраний нами одночлен познача¹ться лiтерою P .

Задамо тепер двiйковий набiр таким чином, щоб всi змiннi, якi входять в P , приймали значення 1, а всi iншi змiннi 0. Тодi кожний одночлен, вiдмiнний вiд P i ÿêèé ì๠áiëüøå íiæ â P число змiнних, прийма¹ значення 0. Сам же одночлен P прийма¹

значення 1. Таким чином, один з полiномiв прийма¹ значення '0 ©1, à iíøèé Ã0. Àëå '0 = Ã0, оскiльки це ¹ значення однаково¨ частини обох полiномiв. Тому '0 ©1 =6 Ã0, ùî протирiччить тому, що полiноми зображують одну i ту ж функцiю. Теорема доведена.¤

З дано¨ теореми виплива¹ ще один спосiб доведення рiвносильностi формул. А саме, якщо двi формули зводяться до одного i того ж полiнома Жегалкiна, то вони рiвносильнi. Доведемо, наприклад, що

(A ¡! B) ¡! (A ¡! C) ´ A ¡! (B ¡! C):

Ìà¹ìî x ¡! y ´ x¹ _y ´ xy¹ _x¹y¹_xy _xy¹ ´ xy¹ _x¹y¹_xy ´ (x ©1)y ©(x ©1)(y ©1) ©xy ´ xy © y © xy © x © y © 1 © xy ´ xy © x © 1: Îòæå, x ¡! y ´ xy © x © 1. Таким чином,

(A ¡! B) ¡! (A ¡! C) ´ (AB © A © 1) ¡! (AC © A © 1) ´

26

´(AB © A © 1)(AC © A © 1) © (AB © A © 1) © 1

´ABC © AB © AB © AC © A © A © AC © A © 1 © AB © A © 1 © 1 ´

´ABC © AB © 1;

A ¡! (B ¡! C) ´ A ¡! (BC © B © 1) ´

´A(BC © B © 1) © A © 1 ´ ABC © AB © A © A © 1 ´

´ABC © AB © 1:

Отже, обидвi формули зводяться до одного i того ж полiнома Жегалкiна, а це й означа¹, що вони рiвносильнi.

27

1.5Замкненi класи булевих функцiй. Теорема про функцiональну повноту

Функцi¨, якi зберiгають константи. Самодво¨стi функцi¨. Монотоннi функцi¨. Лiнiйнi функцi¨. Теорема Поста про функцiональну повноту системи булевих функцiй.

1. Будемо казати, що булева функцiя f(x1; : : : ; xn) зберiга¹ константу нуль (вiдповiдно, одиницю), якщо f(0; : : : ; 0) = 0 (âiäïîâiäíî, f(1; : : : ; 1) = 1). Множину

всiх функцiй, якi зберiгають ноль, позначимо через K0, а якi зберiгають одиницю через K1.

Ëåìà 1. Суперпозицiя функцiй, якi зберiгають константу ноль, ¹ знову функцiя, яка зберiга¹ константу ноль. Iнакше кажучи, клас функцiй K0 замкнений вiдносно

суперпозицiй.

Доведення. Справдi, нехай f; f1; : : : ; fn 2 K0. Розглянемо функцiю F (x1; : : : ; xn), яка ¹ суперпозицi¹ю даних функцiй i визнача¹ться рiвнiстю:

F (x1; : : : ; xn) = f(f1(x1; : : : ; xn); : : : ; fn(x1; : : : ; xn)):

(1.5.1)

Покажемо, що ця функцiя належить класу K0. Ìà¹ìî

F (0; : : : ; 0) = f(f1(0; : : : ; 0); : : : ; fn(0; : : : ; 0)) = f(0; : : : ; 0) = 0:

Îòæå, F (x1; : : : ; xn) 2 K0.

¤

Íàñëiäîê 5. Повна система булевих функцiй мiстить хоча б одну функцiю, яка не зберiга¹ константу ноль.

Справдi, якщо припустити, що всi функцi¨ повно¨ системи зберiгають константу ноль, то звiдси випливатиме, що будь-яка булева функцiя також зберiга¹ константу ноль. Але ж це не так, оскiльки, наприклад, iмплiкацiя ноль не зберiга¹ (0 ¡! 0 = 1),

тобто ¡!62K0.

Аналогiчно доводяться такi твердження:

Ëåìà 2. Суперпозицiя функцiй, якi зберiгають константу одиниця, ¹ знову функцiя, яка зберiга¹ константу одиниця. Iнакше кажучи, клас функцiй K1 замкнений

вiдносно суперпозицiй.

Íàñëiäîê 6. Повна система булевих функцiй мiстить хоча б одну функцiю, яка не зберiга¹ константу одиниця.

Всi мiркування аналогiчнi. Зауважимо лише, що сума по модулю два не зберiга¹ одиницю (1 © 1 = 0), тобто © 62K1.

2. Булева функцiя f(x1; : : : ; xn) назива¹ться самодво¨стою, якщо вона на довiльнiй

	парi протилежних	двiйкових наборiв 9 прийма¹ протилежнi значення, тобто вона
	задовольня¹ рiвнiсть:						(1.5.2)
			f(x1; : : : ; xn) = f(¹x1			; : : : ; x¹n)
	9 Двiйковi набори	âèäó (x1; : : : ; xn) i (¹x1; : : : ; x¹n)				називаються протилежними,	наприклад,
	(0; 1; 1; 0; 1; 0) i (1; 0; 0; 1; 0; 1) приклад пари протилежних двiйкових наборiв.

28

для довiльних x1; : : : ; xn 2 f0; 1g.

Множину всiх самодво¨стих булевих функцiй позначимо через Ks.

Ëåìà 3. Суперпозицiя самодво¨стих булевих функцiй ¹ знову самодво¨ста функцiя, тобто клас Ks замкнений вiдносно суперпозицiй.

Доведення. Дiйсно, нехай f; f1; : : : ; fm 2 Ks. Розглянемо функцiю F (x1; : : : ; xn), яка визнача¹ться рiвнiстю (1.5.1). Тодi ми будемо мати:

F (x1; : : : ; xn) = f(f1(x1; : : : ; xn); : : : ; fn(x1; : : : ; xn)) =

=f(f1(x1; : : : ; xn); : : : ; fn(x1; : : : ; xn)) =

=f(f1(¹x1; : : : ; x¹n); : : : ; fn(¹x1; : : : ; x¹n)) = F (¹x1; : : : ; x¹n);

тобто F 2 Ks.

¤

Íàñëiäîê 7. Повна система булевих функцiй мiстить хоча б одну несамодво¨сту функцiю.

Справдi, якщо припустити, що всi функцi¨ повно¨ системи самодво¨стi, то звiдси випливатиме, що будь-яка булева функцiя також буде самодво¨стою. Але ж це не так, оскiльки, наприклад, iмплiкацiя ¹ несамодво¨ста функцiя, бо вона на протилежних наборах (0; 0) i (1; 1) прийма¹ однаковi значення. Отже, ¡!62Ks.

Ëåìà 4. За допомогою пiдстановки функцiй x i x¹ у несамодво¨сту булеву функцiю можна отримати константу.

Доведення. Нехай функцiя f(x1; : : : ; xn) несамодво¨ста, тобто

f(a1; : : : ; an) = f(¹a1; : : : ; a¹n)

(1.5.3)

для деякого двiйкового набору ~a = (a1; : : : ; an). За набором ~a побуду¹мо функцi¨ 'i(x), i = 1; : : : ; n, таким чином:

x;	ÿêùî a	= 0;
'i(x) = ½ x;¹	ÿêùî aii	= 1:	(1.5.4)

З (1.5.4) виплива¹, що 'i(0) = ai, 'i(1) = a¹i для кожного i = 1; : : : ; n. Розглянемо

функцiю	'(x) = f('1	(x); : : : ; 'n(x));	(1.5.5)

тодi матимемо

'(0) = f('1(0); : : : ; 'n(0)) = f(a1; : : : ; an) = f(¹a1; : : : ; a¹n) = f('1(1); : : : ; 'n(1)) = '(1);

тобто '(x) ¹ константа.				¤
3. Кажуть, що набiр ~a = (a1; : : : ; an)	переду¹ набору ~		; : : : ; bn) i це познача¹ться
		b = (b1
~				; : : : ; xn) назива¹ться
~a Á b, ÿêùî ai 6 bi äëÿ âñiõ i = 1; : : : ; n. Булева функцiя f(x1
монотонною, якщо для довiльних наборiв ~a		, ~	~	~
		b ç òîãî, ùî ~a Á b, виплива¹ f(~a) 6 f(b).

Клас всiх монотонних функцiй позначимо через Km.

29

Ëåìà 5. Суперпозицiя монотонних булевих функцiй ¹ знову монотонна функцiя, тобто клас Km замкнений вiдносно суперпозицiй.

Доведення.

~

b, то, очевидно,

~ ~

(f1(b); : : : ; fn(b)),

Нехай f; f1; : : : ; fn 2 Km i F

~

fi(~a) 6 fi(b) для кожного звiдки

визнача¹ться згiдно (1.5.1). Якщо ~a Á

i = 1; : : : ; n, òîìó (f1(~a); : : : ; fn(~a)) Á

~	~	~
F (~a) = f(f1(~a); : : : ; fn(~a)) Á f(f1(b); : : : ; fn(b)) = F (b);
îòæå, F 2 Km.		¤

Íàñëiäîê 8. Повна система булевих функцiй мiстить хоча б одну немонотонну функцiю.

Справдi, якщо припустити, що всi функцi¨ повно¨ системи монотоннi, то звiдси
випливатиме, що будь-яка булева функцiя також буде монотонною. Але ж це не так,
оскiльки, наприклад, еквiвалентнiсть ¹ немонотонна функцiя, оскiльки iснують двiйковi
набори ~a = (0; 0)	i ~	~
	b	= (0; 1) òàêi, ùî ~a Á b, àëå 0 Ã! 0 = 1 i 0 Ã! 1 = 0. Îòæå,

Ã!62Km.

Ëåìà 6. За допомогою пiдстановки у немонотонну функцiю констант 0 i 1, а також функцi¨ x, можна отримати x¹.

Доведення. Нехай f(x1; : : : ; xn) ¹ немонотонна функцiя. Це означа¹, що iснують

, ~	~	~
такi двiйковi набори ~a = (a1; : : : ; an) b	= (b1; : : : ; bn), ùî ~a Á b, àëå f(~a) >	f(b). Ç

~

останнього виплива¹, що f(~a) = 1, f(b) = 0. Побуду¹мо тепер послiдовнiсть сусiднiх

~

наборiв ~a0;~a1;~a2; : : : ;~am 10 таких, що ~a = ~a0 Á ~a1 Á ~a2 Á : : : Á ~am = b. Îñêiëüêè

f(~a0) = 1 i f(~am) = 0, то знайдуться такi сусiднi набори ~ak i ~ak+1, ùî f(~ak) = 1 i f(~ak+1) = 0. Припустимо, що цi набори мають такий вид:

~ak = (a1; : : : ; ai¡1; 0; ai+1; : : : ; an); ~ak+1 = (a1; : : : ; ai¡1; 1; ai+1; : : : ; an);

äå a1; : : : ; ai¡1; ai+1; : : : ; an 2 f0; 1g. Розглянемо функцiю

g(x) = f(a1; : : : ; ai¡1; x; ai+1; : : : ; an):
Ìà¹ìî g(0) = f(~ak) = 1 i g(1) = f(~ak+1) = 0, òîìó g(x) = x¹.	¤

4. Булева функцiя f(x1; : : : ; xn) назива¹ться лiнiйною, якщо вона пода¹ться полiномом Жегалкiна першого степеня, тобто якщо вона ма¹ вид:

f(x1; : : : ; xn) = anxn © an¡1xn¡1 © : : : © a1x1 © a0;

äå a0; a1; : : : ; an 2 f0; 1g. Клас всiх лiнiйних булевих функцiй позначимо через Kl.

Ëåìà 7. Суперпозицiя лiнiйних булевих функцiй ¹ знову лiнiйна функцiя, тобто клас Kl замкнений вiдносно суперпозицiй.

10 Двiйковi набори ~ai i ~ai+1 називаються сусiднiми, якщо вони вiдрiзняються рiвно однi¹ю компонентою, наприклад, (0; 1; 0; 1; 0) i (0; 1; 0; 1; 1) сусiднi набори.

30