
МААТЛОГИКА
.pdf
Теорема 18 (теорема про повноту). Якщо формула тавтологi¹ю, то вона ¹ теоремою числення висловлень.
Доведення. Нехай формула A ¹ тавтологiя, p01; : : : ; p0k логiчнi змiннi, що входять â A. При довiльному розподiлi iстинностних значень змiнних p01; : : : ; p0k за лемою 2.2.1 ìà¹ìî p01; : : : ; p0k ` A, îñêiëüêè A0 = A. Îòæå, êîëè jpkj = 1 ìà¹ìî p01; : : : ; p0k¡1; pk ` jpkj = 0, òî p01; : : : ; p0k¡1; » pk ` A. Звiдси за теоремою дедукцi¨ отриму¹мо ` pk ¡! A i p01; : : : ; p0k¡1 `» pk ¡! A. За лемою 10 (g) ма¹мо За лемою 10 (f)
` (pk ¡! A) ¡! ((» pk ¡! A) ¡! A);
тому по МР виводимо p0 |
; : : : ; p0 |
( |
p |
k ¡! |
A) |
¡! |
A, звiдки знову за МР отриму¹мо |
|
p10 ; : : : ; pk0 |
1 |
k¡1 |
` » |
|
|
|
||
¡1 ` A. Продовжуючи аналогiчнi мiркування далi, ми отрима¹мо в результатi |
||||||||
` A, що i треба було довести. |
|
|
|
|
|
¤ |
||
Íàñëiäîê 11. Якщо вираз B мiстить знаки »; ¡!; ^; _; Ã! i ¹ скороченням для деяко¨ формули A числення висловлень, то B ¹ тавтологi¹ю тодi i тiльки тодi, коли A ¹ теорема числення висловлень.
2. Ма¹ мiсце наступна теорема про несуперечнiсть числення висловлень.
Теорема 19. Числення висловлень несуперечлива формальна теорiя, тобто не iсну¹ тако¨ формули A, ùîá A i » A одночасно були теоремами числення висловлень.
Справдi, згiдно твердженню 1 кожна теорема числення висловлень ¹ тавтологiя. Заперечення тавтологi¨ не ¹ тавтологi¹ю. Отже, нi для жодно¨ формули A неможливо,
ùîá A i » A були теоремами числення висловлень.
3. Розглянемо тепер питання про незалежнiсть аксiом числення висловлень.
Означення 5. Пiдмножина X множини всiх аксiом назива¹ться незалежною, якщо деяка формула з X не може бути виведена за допомогою правил виведення з аксiом, що не входять в X.
Теорема 20. Кожна iз схем аксiом A1 ¡A3 визнача¹ незалежну множину аксiом.
Доведення. а) Незалежнiсть A1. На множинi з трьох елементiв f0; 1; 2g задамо
операцi¨ »; ¡! за допомогою таких таблиць: |
|
|
|
|
|||||||
|
|
|
|
|
|
|
Формула |
|
A, яка прийма¹ значення 0 для |
||
|
|
|
|
A |
B |
A ¡! B |
|
||||
|
|
|
|
довiльних |
значень змiнних |
назива¹ться |
|||||
|
|
|
|
0 |
0 |
0 |
|||||
|
|
|
|
видiленою. Modus ponens зберiга¹ властивiсть |
|||||||
|
|
|
|
1 |
0 |
2 |
|||||
|
|
|
|
"бути видiленою формулою", тобто якщо A, |
|||||||
|
A |
» A |
|
2 |
0 |
0 |
|||||
|
|
A ¡! B |
¹ видiленi формули, то i |
B |
¹ âèäiëåíà |
||||||
|
|
|
|
|
|||||||
|
0 |
1 |
|
0 |
1 |
2 |
|
|
|
||
|
1 |
1 |
|
1 |
1 |
2 |
формула. Неважко перевiрити, що кожна |
||||
|
|
аксiома, яка отриму¹ться за схемою A2 i A3, |
|||||||||
|
2 |
0 |
|
2 |
1 |
0 |
також буде видiленою. Отже, видiленою буде i |
||||
|
|
|
|
0 |
2 |
2 |
|||||
|
|
|
|
кожна формула, яка виводиться iз схем A2 i A3 |
|||||||
|
|
|
|
1 |
2 |
0 |
за допомогою modus ponens. Однак формула |
||||
|
|
|
|
2 |
2 |
0 |
p1 ¡! (p2 |
¡! p1), яка явля¹ собою частинний |
|||
|
|
|
|
|
|
|
|||||
випадок A1 не ¹ видiленою, оскiльки вона прийма¹ значення 2 при jp1j = 1 i jp2j = 2.
41

б) Незалежнiсть A2. На множинi з трьох елементiв f0; 1; 2g задамо операцi¨ »; ¡! за допомогою таких таблиць:
|
|
|
A |
B |
A ¡! B |
|
|
|
0 |
0 |
0 |
|
|
|
1 |
0 |
0 |
A |
» A |
|
2 |
0 |
0 |
0 |
1 |
|
0 |
1 |
2 |
1 |
0 |
|
1 |
1 |
2 |
2 |
1 |
|
2 |
1 |
0 |
|
|
|
0 |
2 |
1 |
|
|
|
1 |
2 |
0 |
|
|
|
2 |
2 |
0 |
Формула A, яка прийма¹ значення 0 для
довiльних значень змiнних назива¹ться гротескною. Modus ponens зберiга¹ властивiсть "бути гротескною формулою", тобто якщо A, A ¡! B ¹ гротескнi формули, то i B ¹
гротескна формула. Неважко перевiрити, що кожна аксiома, яка отриму¹ться за схемою A1 i
A3, також буде гротескною. Отже, гротескною
буде i кожна формула, яка виводиться iз схем A1 i A3 за допомогою modus ponens. Однак
частинний випадок схеми A2
(p1 ¡! (p2 ¡! p3)) ¡! ((p1 ¡! p2) ¡! (p1 ¡! p3))
не ¹ гротескною, оскiльки при jp1j = 0, jp2j = 0 i jp3j = 1 формула прийма¹ значення 2. в) Незалежнiсть A3. Для довiльно¨ формули A через h(A) позначимо формулу, яка отриму¹ться з A витиранням всiх входжень знака заперечення. Для кожного
часткового випадку A ñõåì A1 i A2 формула h(A) ¹ тавтологiя. Modus ponens зберiга¹ властивiсть "мати в якостi h(A) тавтологiю", тобто якщо h(A) i h(A ¡! B) ¹ тавтологi¨,
òî h(B) тавтологiя, оскiльки h(A ¡! B) спiвпада¹ з формулою h(A) ¡! h(B).
Отже, кожна формула A, яка виводиться з схем A1 i A2 за допомогою modus ponens в якостi h(A) ма¹ тавтологiю. Але формула h((» p1 ¡!» p1) ¡! ((» p1 ¡! p1) ¡! p1)) спiвпада¹ з формулою (p1 ¡! p1) ¡! ((p1 ¡! p1) ¡! p1), а вона не ¹ тавтологi¹ю. Таким чином, аксiома (» p1 ¡!» p1) ¡! ((» p1 ¡! p1) ¡! p1), яка ¹ частковим випадком A3, не виводиться з A1 i A2 за допомогою modus ponens. ¤
3 Логiка предикатiв
3.1 Предикати i квантори
Предикат, область iстинностi предиката. Логiчнi функцi¨. Операцi¨ над предикатами. Квантори, вiльнi i зв'язанi змiннi. Формули логiки предикатiв. Iстиноснi значення формул логiки предикатiв. Рiвносильнiсть формул логiки предикатiв. Випереджена нормальна форма.
1. Нехай M1; M2; : : : ; Mn ¹ деякi множини, x1; x2; : : : ; xn äåÿêi çìiííi, ÿêi
набувають значень вiдповiдно з даних множин, тодi кожне стверджувальне речення, яке мiстить данi змiннi i ста¹ висловленням при кожнiй замiнi ¨х елементами з вiдповiдних множин, назива¹ться n-мiсним предикатом. Наприклад, над множиною
натуральних чисел речення "x просте число"¹ одномiсний предикат, а "x êîõ๠y"¹
двомiсний предикат на множинi людей. Предикати ми будемо позначати таким чином:
P (x1; x2; : : : ; xn), R(x) àáî Q(x; y). Çìiííi x1; x2; : : : ; xn
змiнними.
Нехай далi P (x1; : : : ; xn) ¹ n-мiсний предикат, визначений на множинах M1; : : : ; Mn, тодi логiчною функцi¹ю, що вiдповiда¹ даному предикату, назива¹ться функцiя
¸P : M1 £ ¢ ¢ ¢ £ Mn ! f0; 1g;
де для довiльних a1 2 M1; : : : ; an 2 Mn за означенням ма¹мо
¸P (a1; : : : ; an) = jP (a1; : : : ; an)j:
Часто поняття логiчно¨ функцi¨ ототожню¹ться з поняттям предиката. Це поясню¹ться тим, що в математичнiй логiцi нас не цiкавить змiстовна суть предиката, нам важливо знати яке iстиносне значення ставиться у вiдповiднiсть за допомогою даного предиката тiй чи iншiй послiдовностi елементiв.
Äëÿ n-мiсного предиката P (x1; : : : ; xn), äå xi 2 Mi, i = 1; : : : ; n, через DP будемо позначати його область iстинностi, яка визнача¹ться таким чином:
DP = f(a1; : : : ; an) j jP (a1; : : : ; an)j = 1g ½ M1 £ ¢ ¢ ¢ £ Mn:
Наприклад, якщо P (x; y) означа¹ предикат x2 + y2 6 1 на множинi дiйсних чисел R, òî DP = f(x; y) 2 R £ Rj x2 + y2 6 1g, тобто DP ¹ êðóã ðàäióñà 1 з центром в початку
координат.
Оскiльки предикати для конкретних значень предметних змiнних приймають одне iз значень "iстина"або "хиба", то ¨х можна зв'язувати логiчними операцiями. Наприклад, якщо A ¹ висловлення, P (x), Q(y; z) предикати, то A _ P (x)
одномiсний предикат, P (x) ¡!» Q(y; z) ¹ тримiсний предикат тощо. В зв'язку з цим
виника¹ задача знаходження областi iстинностi предикатiв, отримуваних за допомогою логiчних операцiй, якщо вiдомi областi iстинностi вихiдних предикатiв. Справедливе таке твердження:
43
Твердження 2. ßêùî P (x) i Q(x) ¹ предикати над множиною M, òî
D»P = M n DP ;
DP ^Q = DP \ DQ;
DP _Q = DP [ DQ;
DP ¡!Q = (M n DP ) [ DQ;
DP Ã!Q = (DP \ DQ) [ ((M n DP ) \ (M n DQ)):
Доведення. Справдi, a 2 D»P означа¹ j » P (a)j = 1, тобто jP (a)j = 0, що означа¹ a 62D»P . Отже, ми довели першу рiвнiсть. Нехай тепер a 2 DP ^Q, тобто j(P ^Q)(a)j = 1. Останн¹ означа¹, що jP (a) ^ Q(a)j = 1, òîìó jP (a)j = 1 i jQ(a)j = 1, тобто a 2 DP i a 2 DQ, òîìó a 2 DP \DQ. Друга рiвнiсть доведена. Третя доводиться аналогiчно. Далi ма¹мо DP ¡!Q = D»P _Q = D»P [ DQ = (M n DP ) [ DQ. Остання рiвнiсть доводиться
аналогiчно. |
¤ |
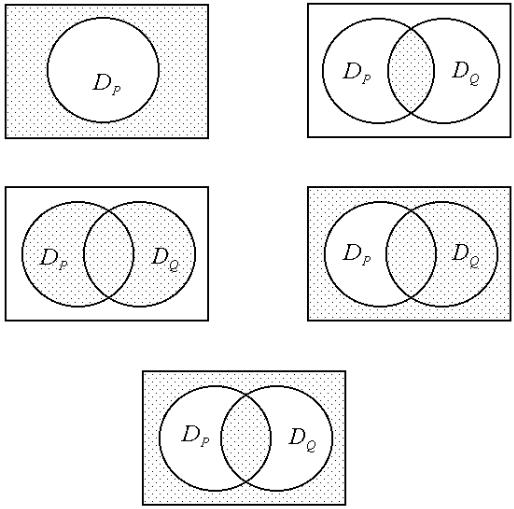
Розглянутi областi iстинностi добре iлюструються нижче дiаграмами Ейлера: |
|
D»P |
DP ^Q |
DP _Q |
DP ¡!Q |
DP Ã!Q
44
2. Нехай P (x) ¹ деякий предикат над множиною M, тодi пiд виразом |
|
(8x)P (x) |
(3.1.1) |
ми будемо розумiти висловлення, яке iстинне, коли P (x) iстинне для кожного елемента з M, i хибне в протилежному випадку. Це висловлення вже не залежить вiд x. Вiдповiдний йому словесний вираз буде такий: "Для всiх x справедливе P (x)". Символ
(8x) назива¹ться квантором загальностi. З даного означення виплива¹, що у випадку необхiдностi вираз (3.1.1) можна розглядати як скорочений запис кон'юнкцi¨ V P (a).
a2M
ßêùî M = fa1; a2; : : : ; ang, то, очевидно, така кон'юнкцiя ма¹ вигляд P (a1) ^ P (a2) ^
: : : ^ P (an).
Далi, пiд виразом |
(9x)P (x) |
(3.1.2) |
|
ми будемо розумiти висловлення, яке iстинне, коли iсну¹ елемент x ç M такий, що P (x) iстинне. Вираз (3.1.2) словесно чита¹ться так: "Iсну¹ x такий, що P (x) справедливе".
Çíàê (9x) назива¹ться квантором iснування. Вiдмiтимо, що (3.1.2) можна розглядати, як скорочення запису a2WM P (a) àáî æ P (a1) _P (a2) _: : : _P (an) при умовi, що множина
M скiнченна, тобто M = fa1; a2; : : : ; ang.
За допомогою логiчних операцiй i кванторiв з висловлень та предикатiв можна утворювати формули логiки предикатiв. Наприклад,
(8x)(A ¡! (9y) » B(x; y)) _ (C Ã! (8z)(9y)D(y; z))
¹ формула логiки предикатiв. Ми бачимо, що однi предметнi змiннi знаходяться в областi дi¨ квантора, а iншi нi. Першi називаються зв'язаними предметними змiнними, а iншi вiльними. Наприклад, у формулi (8x)(P (x) ¡! (9y)Q(y; z)) çìiííi x; y
çâ'ÿçàíi, à z âiëüíà.
3. Нехай D ¹ деяка множина, яка далi буде називатися полем, A формула
логiки предикатiв. Вiдомо, що A може мати змiннi трьох видiв, а саме, логiчнi,
предметнi i предикатнi. Логiчнi змiннi, як вiдомо, приймають значення "iстина", "хиба", предметнi приймають значення з поля D, а предикатнi приймають значення
з множини всiх логiчних функцiй над полем D. Приписуванням для формули A над полем D назива¹ться кожна вiдповiднiсть, яка припису¹ кожнiй n-мiснiй предикатнiй змiннiй n-мiсну логiчну функцiю над D, кожнiй вiльнiй предметнiй змiннiй деякий
елемент поля D, кожнiй логiчнiй змiннiй значення "iстина"або "хиба". Вiдмiтимо, що
логiчна функцiя предиката i його область iстинностi (яка ¹ вiдношенням) однозначно визначають одна-одну, тому часто n-мiснiй предикатнiй змiннiй припису¹ться просто
n-арне вiдношення.
Як приклад розглянемо питання про приписування iстинностних значень для формули
(8x)(P (x) ¡! Q) _ (Q ^ P (y))
над полем D = fa; bg. Згiдно означення приписування одномiснiй предикатнiй змiннiй P (x) ставиться у вiдповiднiсть одна з чотирьох логiчних функцiй:
45
x |
|
¸1(x) |
¸2(x) |
¸3(x) |
¸4(x) |
a |
|
1 |
1 |
0 |
0 |
b |
|
1 |
0 |
1 |
0 |
|
|
|
|
|
|
Ëîãi÷íié çìiííié Q можна приписувати два значення 0 àáî 1, вiльнiй предметнiй змiннiй y також два значення a àáî b. Таким чином, для дано¨ формули можна задати всього 4£ 2£2 = 16 рiзних приписувань значень змiнних. Розглянемо конкретнi два приписування
f1: |
8 y |
b; |
f2: |
8 y |
a; |
|
||
|
> |
Q 7!1; |
|
> |
Q 7!0; |
|
||
|
|
7! |
|
|
7! |
|
||
|
< P (x) ¸ (x); |
|
< P (x) ¸ (x); |
|||||
i знайдемо iстинностнi |
> |
|
|
|
> |
|
|
f1 формула ма¹ значення |
|
: |
|
7!2 |
|
: |
|
7! |
|
|
|
|
|
|
|
1 |
||
значення дано¨ формули для них. При
1, îñêiëüêè
(8x)(¸2(x) ¡! 1) _ (1 ^ ¸2(b)) = (¸2(a) ¡! 1)(¸2(b) ¡! 1) _ (1 ^ 0) = 1 ¢ 1 _ 0 = 1 _ 0 = 1;
ïðè f2 формула прийма¹ значення 0, îñêiëüêè
(8x)(¸1(x) ¡! 0) _ (0 ^ ¸1(a)) = (¸1(a) ¡! 0)(¸1(b) ¡! 0) _ (0 ^ 1) =
=(1 ¡! 0)(1 ¡! 0) = 0 ¢ 0 _ 0 = 0 _ 0 = 0:
4.Поняття рiвносильностi формул вводиться також i в логiцi предикатiв. А саме, двi формули A i B логiки предикатiв називаються рiвносильними (це познача¹ться
через A ´ B), якщо вони приймають однаковi iстинностнi значення при кожному приписуванi значень змiнним над довiльним полем.
Теорема 21. В логiцi предикатiв виконуються такi рiвносильностi:
1: » (8x)A(x) ´ (9x) » A(x); 2: » (9x)A(x) ´ (8x) » A(x);
3: (8x)(A(x) ^ B) ´ (8x)A(x) ^ B; 4: (9x)(A(x) ^ B) ´ (9x)A(x) ^ B; 5: (8x)(A(x) _ B) ´ (8x)A(x) _ B; 6: (9x)(A(x) _ B) ´ (9x)A(x) _ B;
7: (8x)(A(x) ¡! B) ´ (9x)A(x) ¡! B; 8: (9x)(A(x) ¡! B) ´ (8x)A(x) ¡! B; 9: (8x)(B ¡! A(x)) ´ B ¡! (8x)A(x); 10: (9x)(B ¡! A(x)) ´ B ¡! (9x)A(x);
де предметна змiнна x не входить вiльно в формулу B.
46
Доведення. Доведемо, наприклад, властивiсть 9. Нехай j(8x)(B ¡! A(x))j = 0,
тобто знайдеться x0 òàêå, ùî jB ¡! A(x0)j = 0. Çâiäñè ìà¹ìî jBj = 1 i jA(x0)j = 0. Îòæå, j(8x)A(x)j = 0, òîìó jB ¡! (8x)A(x)j = 0. Обернене доводиться аналогiчно. Таким
чином, формули (8x)(B ¡! A(x)) i B ¡! (8x)A(x) одночасно приймають однаковi значення, тобто вони рiвносильнi. ¤
Означення 6 Формула (Q1x1) : : : (Qnxn)A, äå (Qixi) ¹ квантор загальностi або
iснування, xi 6= xj ïðè i 6= j i A не мiстить кванторiв, назива¹ться випередженою нормальною формою.
Очевидно, як виплива¹ з теореми 21, кожна формула логiки предикатiв може бути зведена до випереджено¨ нормально¨ форми. Покажемо цю процедуру на конкретному прикладi.
Приклад. Знайти випереджену нормальну форму для формули:
(8x)A(x) ¡! (8x)(B(x; y) ¡!» (8z)C(y; z)):
Ìà¹ìî
(8x)A(x) ¡! (8x)(B(x; y) ¡!» (8z)C(y; z)) ´
´(8x)A(x) ¡! (8x)(B(x; y) ¡!» (8z)C(y; z)) ´
´(9x)(A(x) ¡! (8x)(B(x; y) ¡!» (8z)C(y; z))) ´
´(9x)(A(x) ¡! (8u)(B(u; y) ¡!» (8z)C(y; z))) ´
´(9x)(8u)(A(x) ¡! (B(u; y) ¡!» (8z)C(y; z))) ´
´(9x)(8u)(A(x) ¡! (B(u; y) ¡! (9z) » C(y; z))) ´
´(9x)(8u)(9z)(A(x) ¡! (B(u; y) ¡!» C(y; z))):
47
3.2 Загальнозначущiсть i виконуванiсть формул в логiцi преди- |
||||||
|
êàòiâ |
|
|
|
|
|
|
Загальнозначущiсть i виконуванiсть формул логiки предикатiв. |
|||||
|
Приклад формули, яка виконувана в нескiнченному полi, але не |
|||||
|
виконувана |
у скiнченному полi. Формулювання проблеми вирiшення |
||||
|
в логiцi предикатiв. Розв'язання проблеми вирiшення для формул у |
|||||
|
випередженiй нормальнiй формi, якi мiстять квантори загальностi, |
|||||
|
що передують кванторам iснування. Проблема вирiшення для формул |
|||||
|
з одномiсними предикатами. Застосування мови логiки предикатiв |
|||||
|
для запису математичних тверджень, логiчний наслiдок в логiцi |
|||||
|
предикатiв. |
|
|
|
|
|
1. |
Формула |
ëîãiêè |
предикатiв |
назива¹ться |
загальнозначущою |
в даному |
полi, якщо вона прийма¹ значення "iстина"при кожному приписуваннi значень |
||||||
предикатним i вiльним |
предметним |
çìiííèì íàä |
цим полем. Якщо |
формула A |
||
загальнозначуща над довiльним полем, то вона назива¹ться просто загальнозначущою. Цей факт познача¹ться символом j= A. Доведемо, наприклад, наступна формула
загальнозначуща:
j= (8x)P (x) _ (8x)Q(x) ¡! (8x)(P (x) _ Q(x)): |
(3.2.1) |
Справдi, припустимо, що формула (3.2.2) не ¹ загальнозначущою. Це означа¹, що знай- |
||||
деться поле i таке приписування f: |
P (x) P ¤(x); |
|
12 |
|
7! |
над цим полем, |
що формула |
||
½ |
Q(x) 7!Q¤(x) |
|
||
(3.2.2) прийма¹ значення "хиба". Тодi, очевидно,
j(8x)P ¤(x) _ (8x)Q¤(x)j = 1 i j(8x)(P ¤(x) _ Q¤(x))j = 0:
З останньо¨ рiвностi виплива¹, що в даному полi знайдеться такий елемент a, ùî jP ¤(a)_
Q¤(a)j = 0, çâiäêè jP ¤(a)j = 0 i jQ¤(a)j = 0. Таким чином, j(8x)P ¤(x)j = 0 i j(8x)Q¤(x)j =
0, òîìó j(8x)P ¤(x) _ (8x)Q¤(x)j = 0. Ми отримали протирiччя. Отже, формула (3.2.2)
загальнозначуща.
Далi, формула логiки предикатiв назива¹ться виконуваною в даному полi, якщо над цим полем знайдеться таке приписування значень предикатним змiнним i вiльним предметним змiнним, при якому формула прийма¹ значення "iстина". Формула назива¹ться виконуваною, якщо вона виконувана в деякому полi. Очевидно, що формула A загальнозначуща тодi i тiльки тодi, коли формула » A не ¹ виконуваною, i
формула A виконувана тодi i тiльки тодi, коли » A не ¹ загальнозначущою. Вiдмiтимо без доведення такi двi теореми:
Теорема 22. Якщо формула логiки предикатiв загальнозначуща в деякому полi, то вона загальнозначуща в кожному полi тi¹¨ ж або меншо¨ потужностi.
Теорема 23. Якщо формула логiки предикатiв виконувана в деякому полi, то вона виконувана в iншому полi тi¹¨ ж або бiльшо¨ потужностi.
12 Вiдмiтимо, що нами позначено через P ¤(x); Q¤(x) логiчнi функцi¨ над даним полем, якi приписуються предикатним змiнним P (x); Q(x).
48
Нехай A формула, x предметна змiнна, що входить в A (â A, êðiì x, можуть бути й iншi предметнi змiннi). Щоб показати залежнiсть A âiä x, будемо писати A(x). Будемо говорити, що формула A(x) âiëüíà äëÿ y, ÿêùî â A вiдсутнi вiльнi входження x, що входять в область дi¨ кванторiв (8y) àáî (9y). Наприклад, формула P (x; y)^(8y)Q(y) âiëüíà äëÿ y, а формула (x = 1) ^ (9y)(y =6 x) вже не ¹ вiльною для y.
Теорема 24. Нехай A(x) формула, вiльна для y. Тодi мають мiсце:
1. j= (8x)A(x) ¡! A(y);
2. j= A(y) ¡! (9x)A(x).
Доведення. Справдi, припустимо, що перша формула не загальнозначуща. Це означа¹, що в деякому полi знайдеться приписування, при якому j(8x)A(x) ¡! A(a)j =
0, äå y 7!a в даному приписуваннi. Отже, j(8x)A(x)j = 1 i jA(a)j = 0. З першо¨ умови виплива¹, що jA(a)j = 1. Отримане протирiччя говорить про те, що припущення було невiрним. Аналогiчно доводиться друге твердження. ¤
Теорема 25. Нехай x; y рiзнi предметнi змiннi, P (x), Q(x), P (x; y) формули, Q довiльна формула, яка не мiстить вiльних входжень x, òîäi
1. j=» (8x)P (x) Ã! (9x) » P (x); 2. j=» (9x)P (x) Ã! (8x) » P (x);
3. j= (8x)(P (x) ^ Q(x)) Ã! (8x)P (x) ^ (8x)Q(x); 4. j= (9x)(P (x) _ Q(x)) Ã! (9x)P (x) _ (9x)Q(x); 5. j= (8x)P (x) _ (8x)Q(x) ¡! (8x)(P (x) _ Q(x)); 6. j= (9x)(P (x) ^ Q(x)) ¡! (9x)P (x) ^ (9x)Q(x);
7. j= (8x)(P (x) ¡! Q(x)) ¡! ((8x)P (x) ¡! (8x)Q(x)); 8. j= ((9x)P (x) ¡! (9x)Q(x)) ¡! (9x)(P (x) ¡! Q(x)); 9. j= (8x)(P (x) Ã! Q(x)) ¡! ((8x)P (x) Ã! (8x)Q(x)); 10. j= ((9x)P (x) Ã! (9x)Q(x)) ¡! (9x)(P (x) Ã! Q(x)); 11. j= (9x)(P (x) ¡! Q(x)) Ã! ((8x)P (x) ¡! (9x)Q(x)); 12. j= ((9x)P (x) ¡! (8x)Q(x)) ¡! (8x)(P (x) ¡! Q(x)); 13. j= (8x)(P (x) ^ Q) Ã! ((8x)P (x) ^ Q);
14. j= (8x)(P (x) _ Q) Ã! ((8x)P (x) _ Q); 15. j= (9x)(P (x) ^ Q) Ã! ((9x)P (x) ^ Q); 16. j= (9x)(P (x) _ Q) Ã! ((9x)P (x) _ Q);
49
17. j= (8x)(P (x) ¡! Q) Ã! ((9x)P (x) ¡! Q); 18. j= (9x)(P (x) ¡! Q) Ã! ((8x)P (x) ¡! Q); 19. j= (8x)(P ¡! Q(x)) Ã! (P ¡! (8x)Q(x)); 20. j= (9x)(P ¡! Q(x)) Ã! (P ¡! (9x)Q(x)); 21. j= (8x)(8y)P (x; y) Ã! (8y)(8x)P (x; y); 22. j= (9x)(9y)P (x; y) Ã! (9y)(9x)P (x; y); 23. j= (9x)(8y)P (x; y) ¡! (8y)(9x)P (x; y).
Доведення тверджень 1 23 проводиться за допомогою звичайних мiркувань.
2. Щоб показати, що теорема 22 для здiйсненностi не ма¹ мiсця, наведемо приклад формули, яка виконувана в нескiнченному полi, але не виконувана в жодному скiнченному полi. Справдi, розглянемо формулу:
³ ´
(8x)(8y)(8z)(9u) » P (x; x) ^ (P (x; y) ^ P (y; z) ¡! P (x; z)) ^ P (x; u) :
Припустимо, що ця формула викону¹ться в деякому полi M. В такому випадку, iсну¹ двомiсна логiчна функцiя ¸(x; y) над цим полем, для яко¨ дана формула iстинна на M.
Неважко бачити, що ¸(x; y) встановлю¹ мiж елементами поля M вiдношення строгого порядку, тому що справедливi умови:
1. » ¸(x; x) для довiльного x 2 M (антирефлексивнiсть);
2. ¸(x; y) ^ ¸(y; z) ¡! ¸(x; z) äëÿ âñiõ x; y; z 2 M (транзитивнiсть).
ßêùî ¸(x; y), то будемо казати, що "x переду¹ y". Вiзьмемо довiльний елемент поля x1, тодi серед елементiв поля повинен знайтись елемент x2, âiäìiííèé âiä x1, такий, що "x1 переду¹ x2". Точно так саме повинен знайтись елемент x3 такий, що "x2 переду¹ x3"i ò.ä.
Отриму¹мо послiдовнiсть елементiв: x1; x2; : : : ; xn; : : :. В силу умов 1 i 2 кожний елемент
послiдовностi вiдмiнний вiд всiх елементiв з меншими iндексами. Але це значить, що кожнi два елемента послiдовностi рiзнi, тому поле M нескiнченне. Отже, ми довели, що
коли дана формула викону¹ться в деякому полi, то воно нескiнченне.
Покажемо тепер, що iсну¹ поле, на якому дана формула викону¹ться. Нехай N ¹ множина натуральних чисел, а P (x; y) означа¹, що x < y, äå x; y 2 N. Тодi дана формула
прийма¹ вигляд:
³ ´
(8x)(8y)(8z)(9u) x x ^ (x < y ^ y < z ¡! x < z) ^ x < u :
Легко бачити, що для натурального ряду цей вираз iстинний.
3. Проблема вирiшення в логiцi предикатiв формулю¹ться так: вказати ефективний спосiб, за допомогою якого для кожно¨ формули логiки предикатiв можна було б визначити чи вона загальнозначуща, чи нi. Як показав вiдомий американський логiк А. Черч, в загальному випадку ця проблема ма¹ негативний розв'язок, тобто не
50
