Глава XIX. Функциональные последовательности и ряды. § 1

Понятие равномерной сходимости

Задачи и упражнения для самостоятельной работы

1.Исследуйте на равномерную сходимость функциональную последовательность:

1.1. , а) x [1; + ∞); б) x [0; 1].

1.2.f_n(x) = arctg(nx), x (0; + _∞)

1.3. , x (0; + ∞)

1.4. , x [0; 1]

2.Исследуйте на равномерную сходимость функциональный ряд:

2.1.

2.2.

ГЛАВА XIX. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ. § 2

Признаки равномерной сходимости

Основные понятия

1. Критерии равномерной сходимости.

Теорема 1. Критерий Коши равномерной сходимости функциональной последовательности. Для того чтобы функциональная последовательность {f_n(x)}сходилась равномерно на множестве Х к некоторой функции f(x), необходимо и достаточно, чтобы > 0 N():n > N,p −

натурального, выполнялось следующее условие: |f_n+p(x) − f_n(x)| < для x X.

Теорема 2. Критерий Коши равномерной сходимости функционального ряда. Для того, чтобы функциональный ряд равномерно сходился к своей сумме необходимо и достаточно, чтобы > 0 N(): n > N,

p − натурального, выполнялось |S_n+p(x) − S(x)|= < для x X.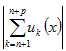

2. Достаточные признаки равномерной сходимости функциональных рядов.

Определение 1. Числовой ряд называется мажорантным (или

мажорирующим) для функционального ряда на множестве X, если n, x X,

^|u_n^(x)| ≤ ^p_n^.

Теорема 3. Признак Вейерштрасса. Если для функционального ряда

на множестве Х существует мажорантный сходящийся числовой ряд , то

исходный функциональный ряд сходится равномерно на множестве Х.

Определение 2. Функциональная последовательность {f_n(x)} называется равномерно ограниченной на множестве Х, если существует константа M такая, что n, x X:

^|f_n ^{(x) |} ≤ ^M.

Теорема 4. Признак Дирихле-Абеля. Рассмотрим ряд .

1. Пусть функциональная последовательность {b_n(x)} не возрастает при каждом x X и сходится к нулю равномерно на множестве X (т.е. b_{n + 1}(x) _≤ b_n(x) x X, а ^{также b}_n^{(x) монотонно стремится к нулю при n} → ∞ ^{на множестве X ).}

2. Последовательность равномерно ограничена на множестве X

Тогда ряд сходится равномерно на множестве X.

Глава XIX. Функциональные последовательности и ряды. § 2

Признаки равномерной сходимости

Примеры решения задач

1.Исследуйте на равномерную сходимость ряд

.

Решение. Найдем мажорантный ряд для данного ряда. Действительно, , а

числовой ряд сходится. Следовательно, ряд сходится равномерно по

признаку Вейрштрасса.

2.Исследуйте на равномерную сходимость ряд на множестве

.

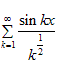
Решение. Обозначим . Последовательность {b_k(x)} убывает,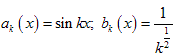

тем самым первое условие теоремы о признаке равномерной сходимости Дирихле-Абеля оказывается выполненным. Воспользуемся оценкой:

при x ≠ 2m, m Z.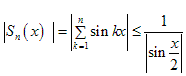

При сколь угодно малом > 0: x [; 2− ] выполняется соотношение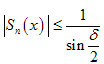

, следовательно, выполнено второе условие теоремы о признаке

равномерной сходимости Дирихле-Абеля, значит, исходный ряд равномерно сходится на [; 2− ].