Занятие 15. Экстремумы функции двух переменных. Элементы теории поля

Пусть функция определена в некоторой области.

Определение. Точканазываетсяточкой максимума (минимума) функции, если существует такая окрестность точки, что для любой точкииз этой окрестности:

.

Точки максимума и минимума функции называются точками экстремума, а значения функции в этих точках –экстремумами.

ТЕОРЕМА. (Необходимое условие экстремума).

Пусть функция дифференцируема в точкеи имеет в ней экстремум. Тогда:

. (1)

Замечание.

Точка , в которой выполнено условие (1), называетсястационарной.

ТЕОРЕМА (Достаточное условие экстремума).

Пусть в стационарной точке и некоторой ее окрестности функцияимеет непрерывные частные производные 2-го порядка включительно. Составим выражение:

.

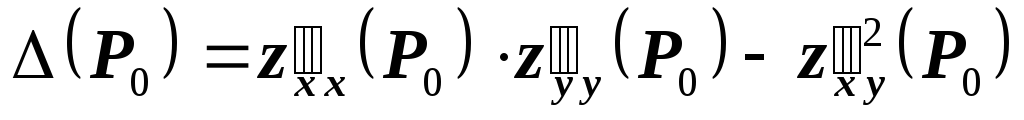Тогда:

1. если 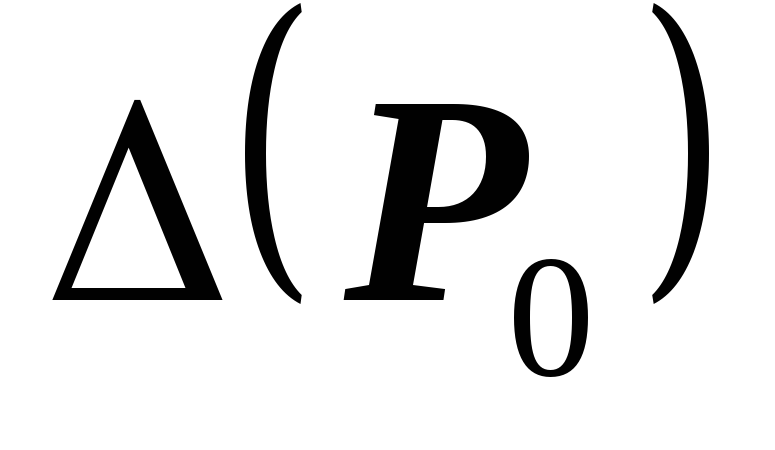, то в точкеесть экстремум; если при этом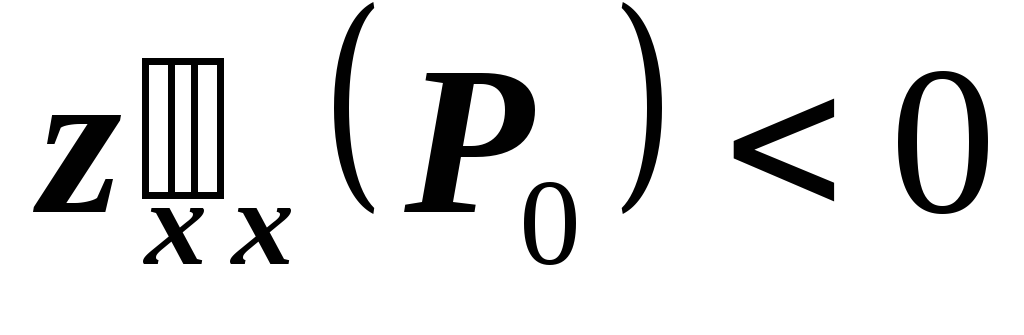, то– то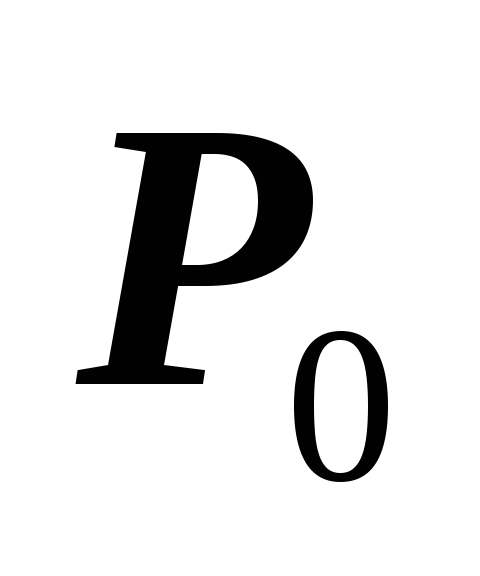чка максимума, а если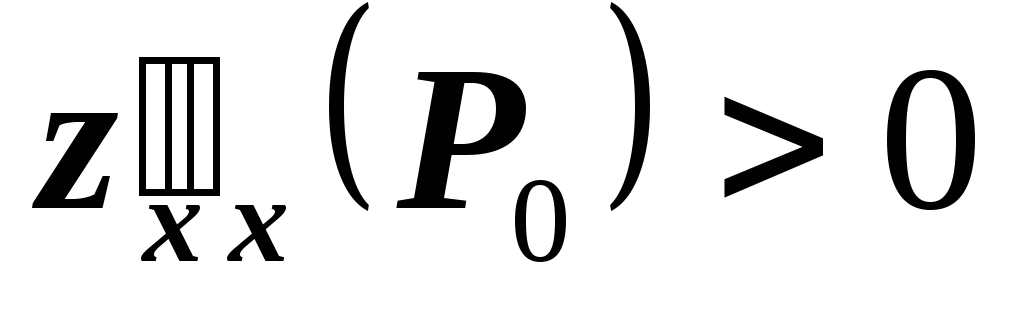, то– то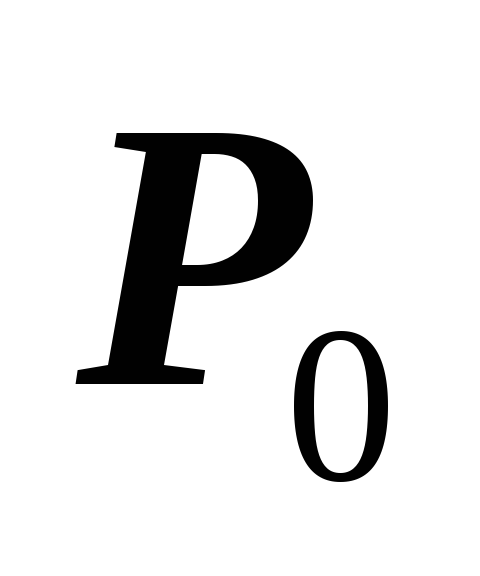чка максимума;

2. если 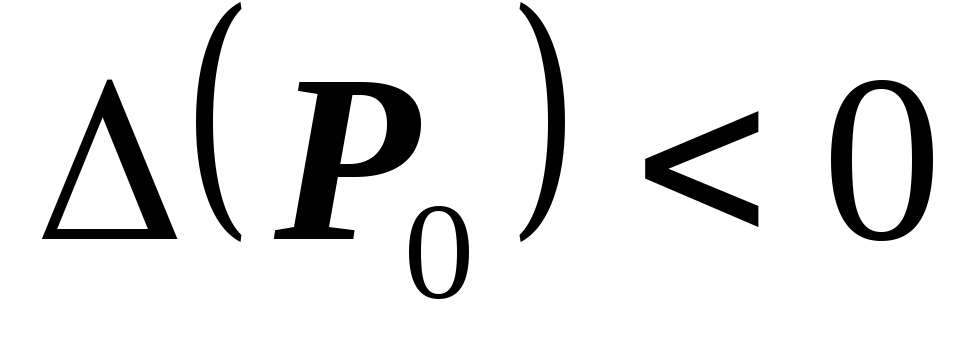, то в точке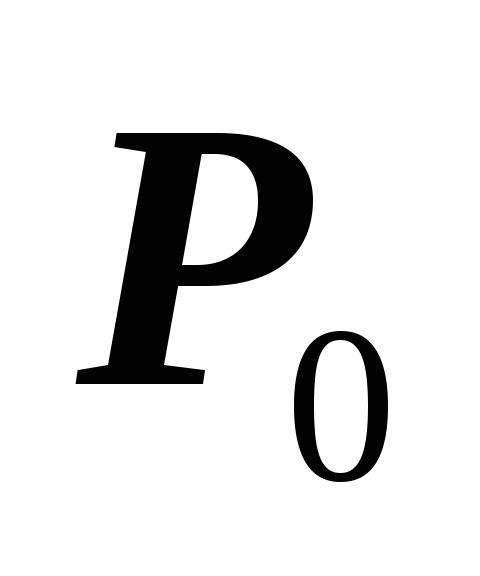нет экстремума;

3. если 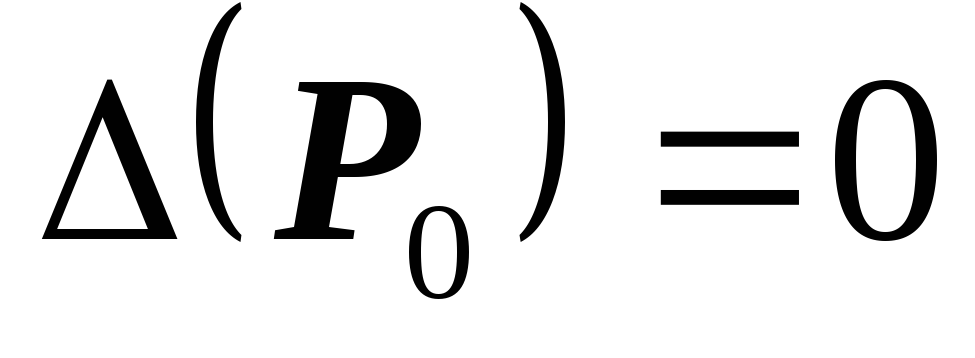, то вопрос о наличии экстремума в точке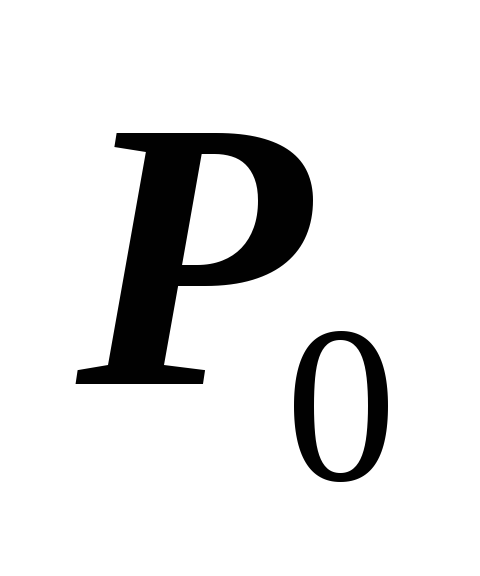остается открытым и нужны другие методы исследования.

1. Рассмотрим функцию z=1+6x-x²-xy-y²

и найдем ее экстремумы.

Найдем все частные производные вида: ,,,,:

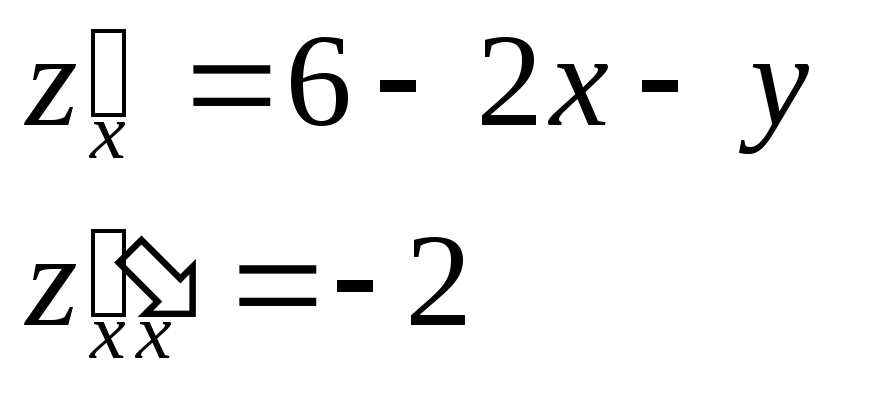
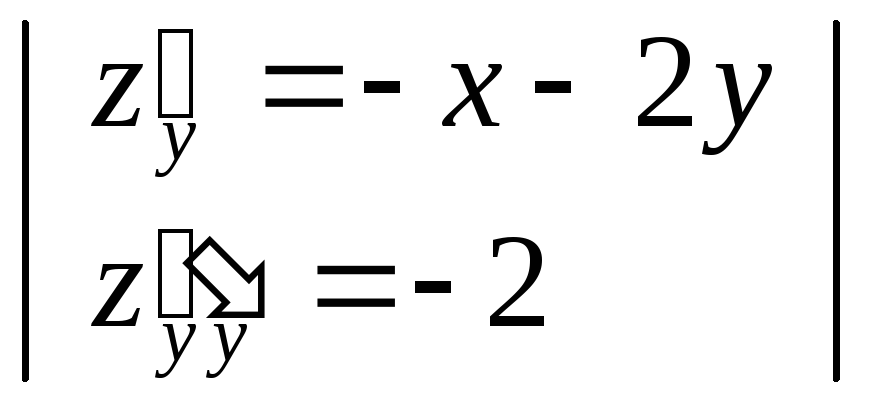
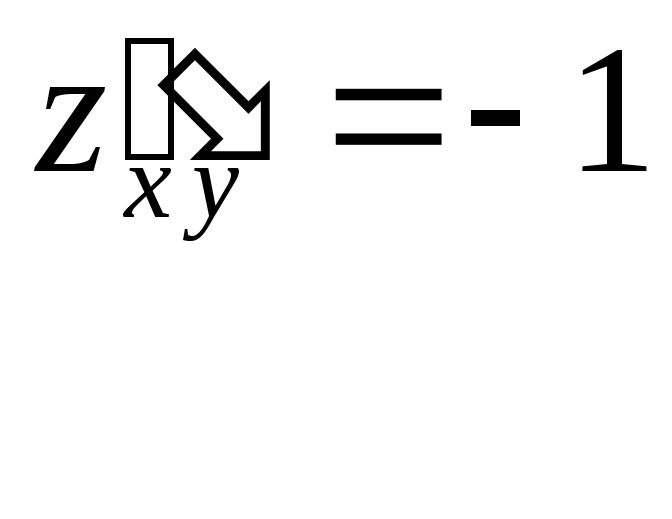
Найдем стационарные точки , для чего решим следующую систему уравнений:

, т.е..

Находим решение этой системы: ,, т.е.– стационарная точка. Найдем:

.

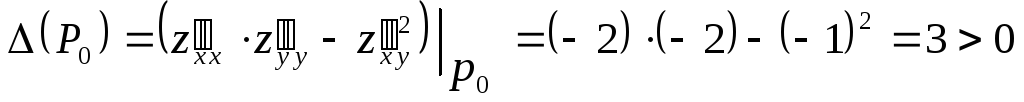Следовательно, в точке есть экстремум. Т.к., то– точка максимума и.

2. Рассмотрим функцию z=x²+y²+x+y+1

и найдем ее экстремумы.

Найдем все частные производные до 2-го порядка включительно: ,,,.

Находим стационарные точки P₀:

стационарная точка.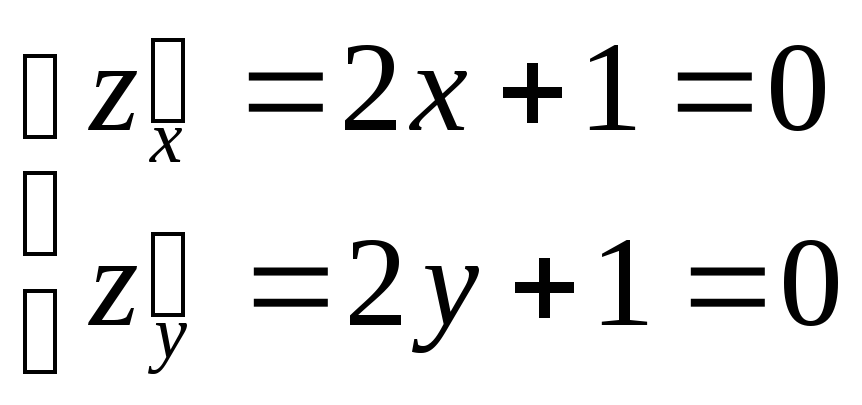

–

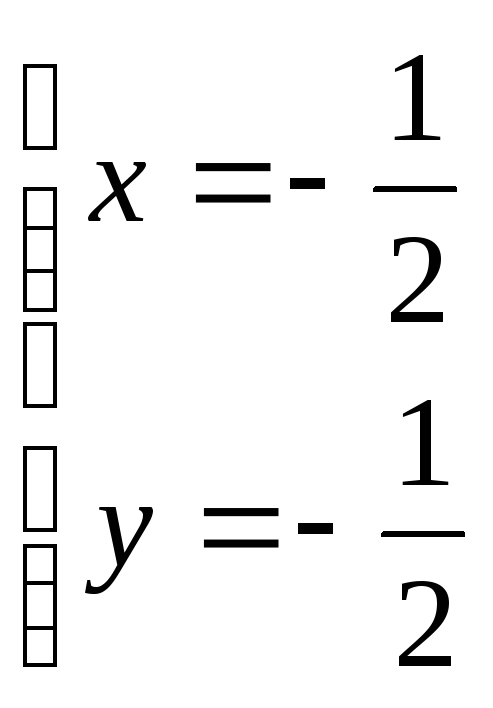
Найдем :

.

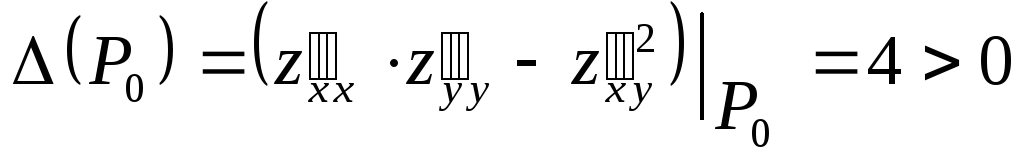Следовательно, в точке есть экстремум. Т.к., то– точка минимум и.

3. Рассмотрим функцию

и найдем ее экстремумы.

Найдем все частные производные до 2-го порядка включительно: ,,

,,.

Затем находим все стационарные точки :

;,.

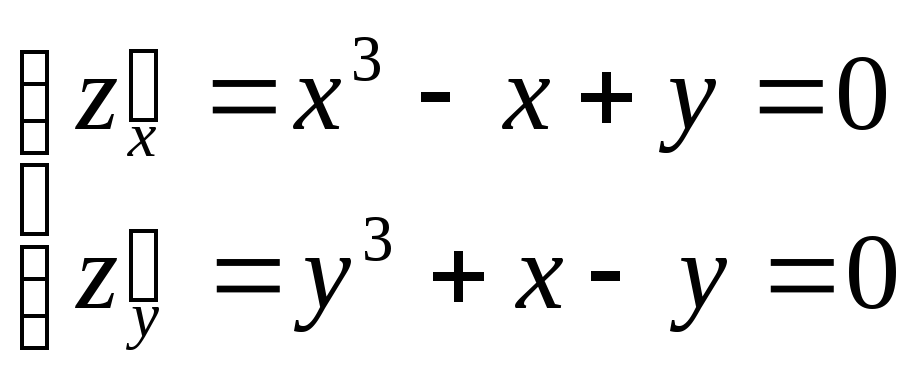
Заметим, что для решения вышеуказанной системы уравнений следует сложить оба уравнения, получив соотношение вида , т.е.. Затем надо подставить в первое уравнение=, получив уравнение видаи решив его, найти абсциссы,,точек,,, а затем и соответствующие ординаты этих точек,,.

Найдем :

;;.

При этом ,, поэтому,– точки минимума и.

Так как , то необходимо дополнительное исследование точкина наличие в ней экстремума. Заметим, что, а в любой окрестностиесть точки, в которыхи в которых(например, еслии:, а еслии:). Следовательно, в точкенет экстремума.

Замечание.

Для того, чтобы найти наибольшее (наименьшее) значение функции в замкнутой ограниченной области , надо найти ее значения в стационарных точках внутри, затем найти наибольшее (наименьшее) значение на границеи выбрать среди полученных чисел максимальное (минимальное).

4. Найти наибольшее и наименьшее

значение функции

в замкнутой области , ограниченной линиями:,,.Область– это треугольник (рис. 4).

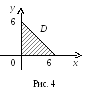
а) Найдем стационарные точки внутри:

.

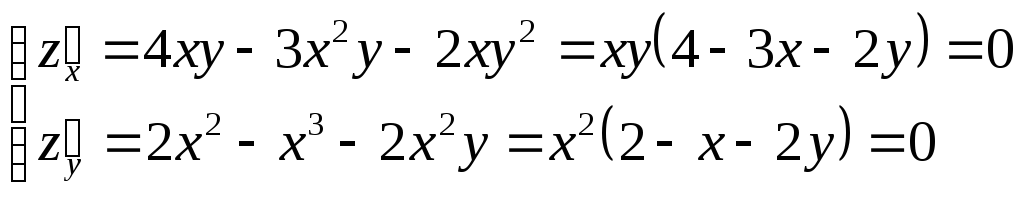Так как внутри ,, то:

– стационарная точка и

.

б) Найдем наибольшее (наименьшее) значениена сторонах вышеуказанного треугольника.

На сторонах, на которых или , или, очевидно,. На 3-ей стороне, задаваемой уравнением, функцияпринимает вид:

.

При этом .

Найдем максимальное и минимальное значение при. Имеем:

или.

Но – граничная точка для отрезка; только– внутренняя точка для отрезка, и в ней – минимум функции,. В граничных точках отрезка. Итак, на границе:,.

Таким образом, в замкнутой области :(достигается внутрив точке) и(достигается на границев точке).