
- •Скворцова м.И., Мудракова о.А.
- •Оглавление
- •Занятие 13. Функции двух переменных: основные определения. Частные производные и дифференциал функции двух переменных.
- •Задачи для самостоятельного решения
- •Занятие 14. Производные сложной и неявно заданной функции Производные сложных функций двух переменных
- •Производная неявно заданной функции
- •2) Существуют и.
- •Задачи для самостоятельного решения
- •Занятие 15. Экстремумы функции двух переменных. Элементы теории поля
- •Элементы теории поля
- •Задачи для самостоятельного решения
- •Занятие 16. Контрольная работа №3 по теме «Дифференциальное исчисление функций двух переменных». Вариант-образец.
- •Занятие 17. Метод наименьших квадратов для обработки результатов эксперимента
- •Перечень вариантов для самостоятельной работы по теме «Метод наименьших квадратов»
- •Список литературы
- •Скворцова Мария Ивановна Мудракова Ольга Александровна
Элементы теории поля
Определения.
Скалярное поле в некоторой области
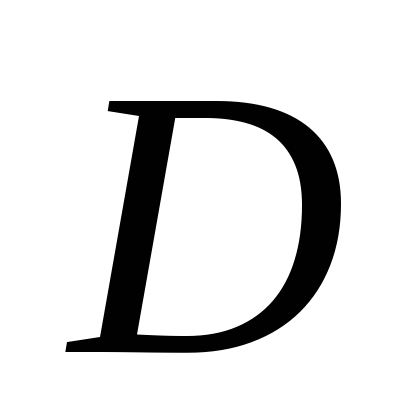 пространства (плоскости) – это функция
пространства (плоскости) – это функция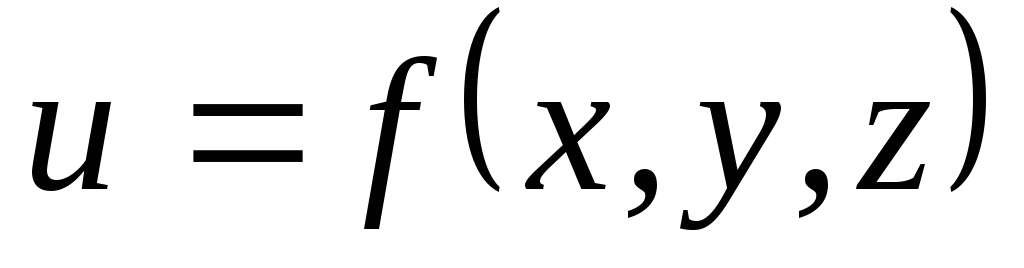
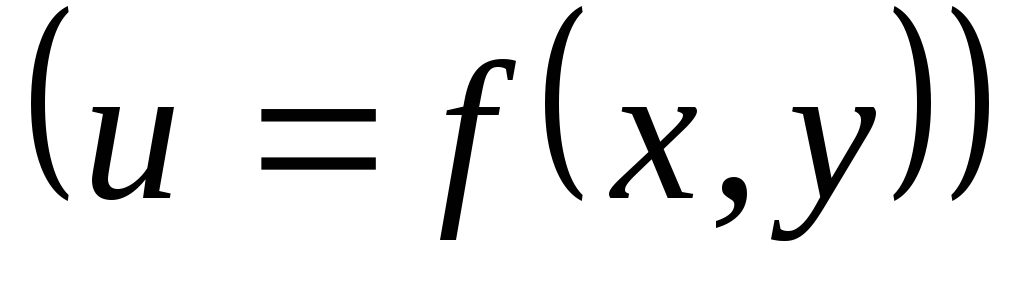 ,
определенная в этой области.
,
определенная в этой области.Градиентом скалярного поля
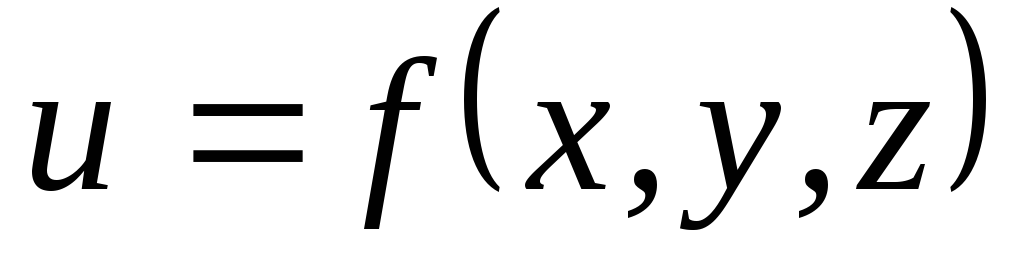 в точке
в точке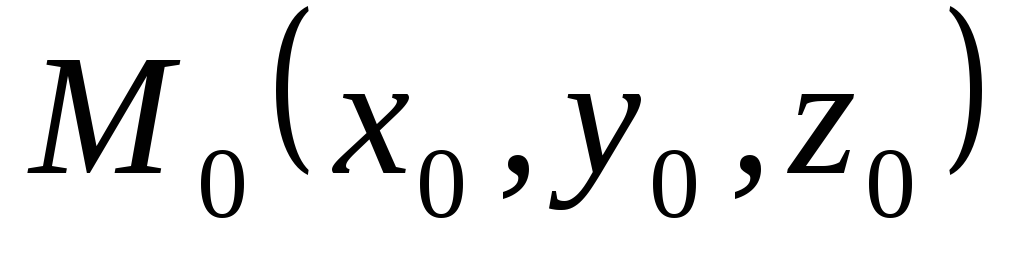 называется вектор
называется вектор
![]() .
.
Пусть в пространстве задано скалярное поле
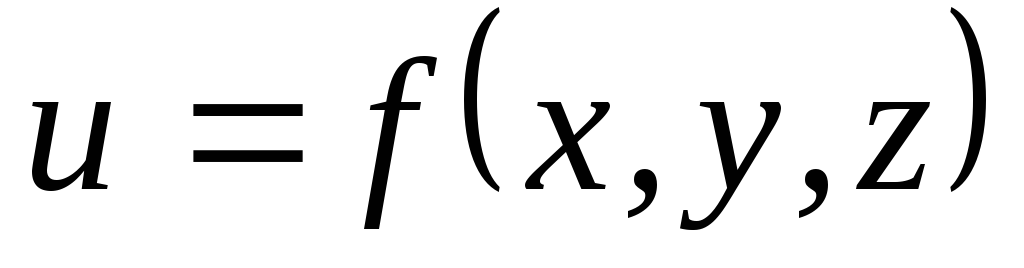 и вектор
и вектор .
.
Производной скалярного поля
![]() по направлению вектора
по направлению вектора![]() в точке
в точке![]() называется число
называется число
![]() ,
,
где
![]() ,
,![]() ,
,![]() – направляющие косинусы вектора
– направляющие косинусы вектора![]() ,
т.е.
,
т.е.![]() ,
,![]() ,
,![]() .
.
Замечания.
Величина
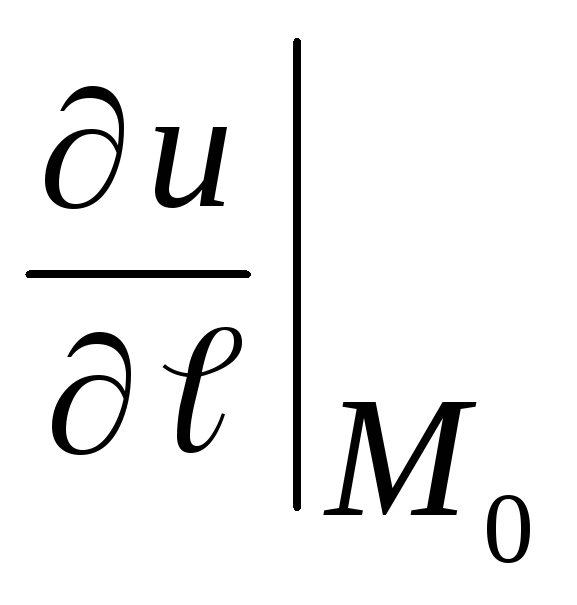 характеризует скорость изменения поля
характеризует скорость изменения поля
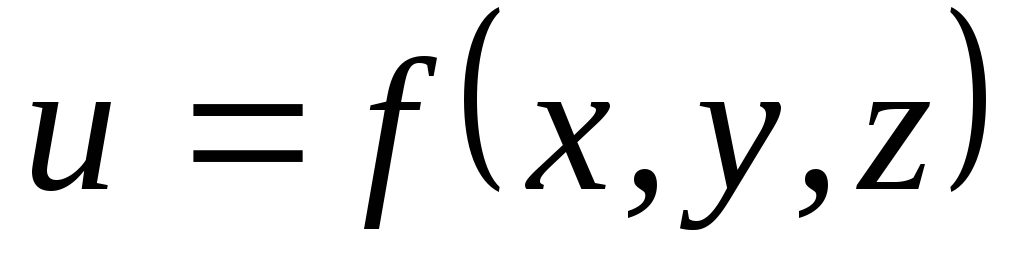 в точке
в точке в направлении
в направлении .
Она равна скалярному произведению
векторов
.
Она равна скалярному произведению
векторов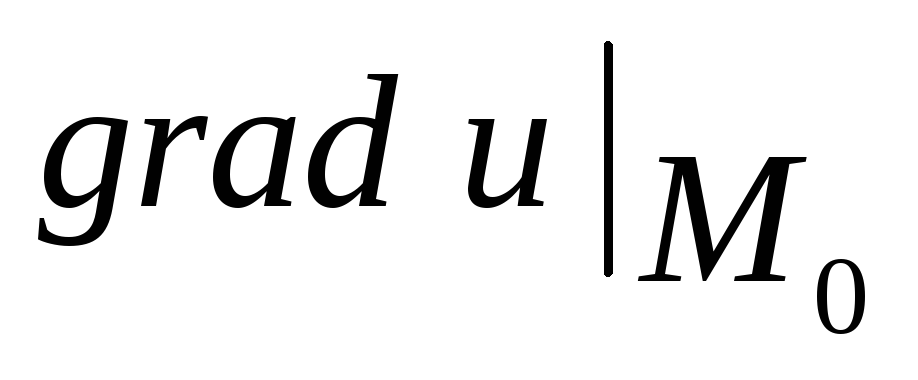 и
и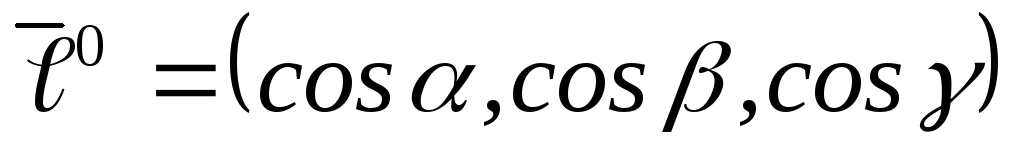 – орта вектора
– орта вектора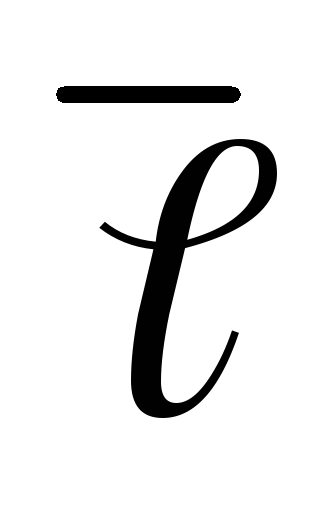 .
.Вектор
 указывает направление максимального
возрастания поля
указывает направление максимального
возрастания поля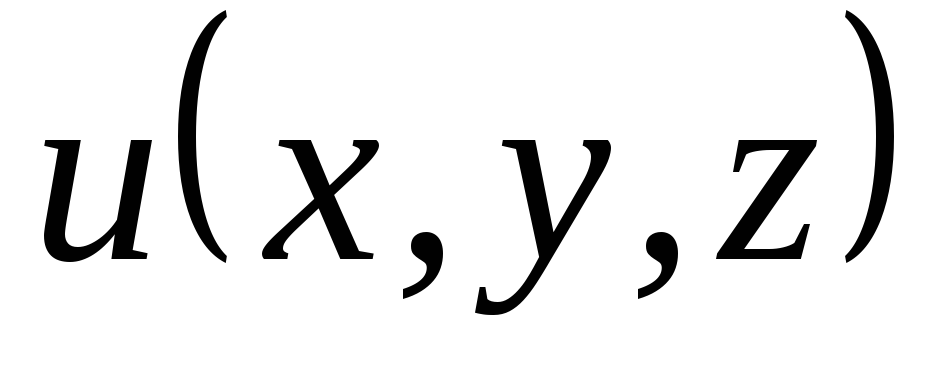 в точке
в точке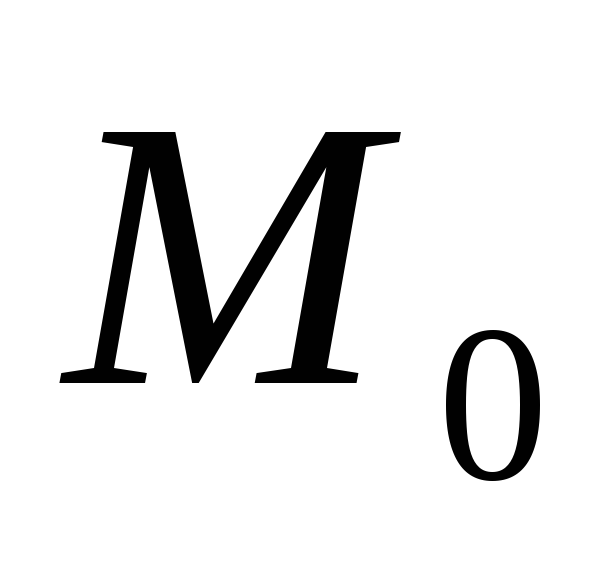 .
Величина
.
Величина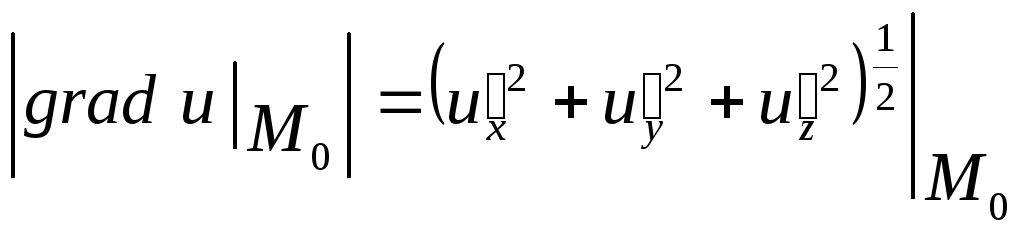 равна скорости возрастания
равна скорости возрастания в точке
в точке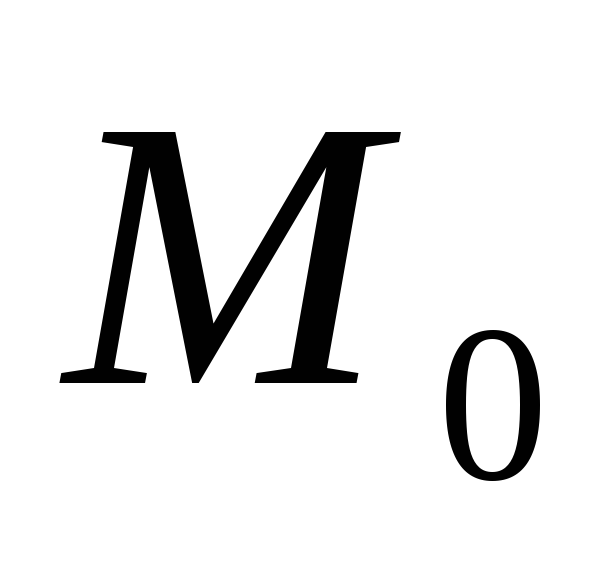 .
.Определения
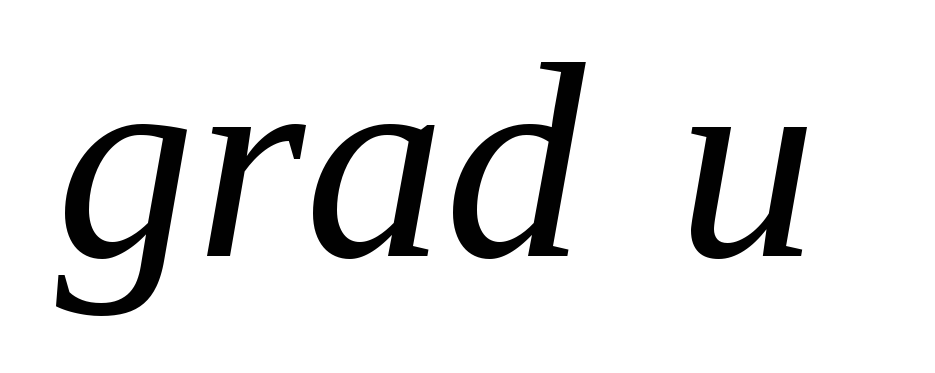 и
и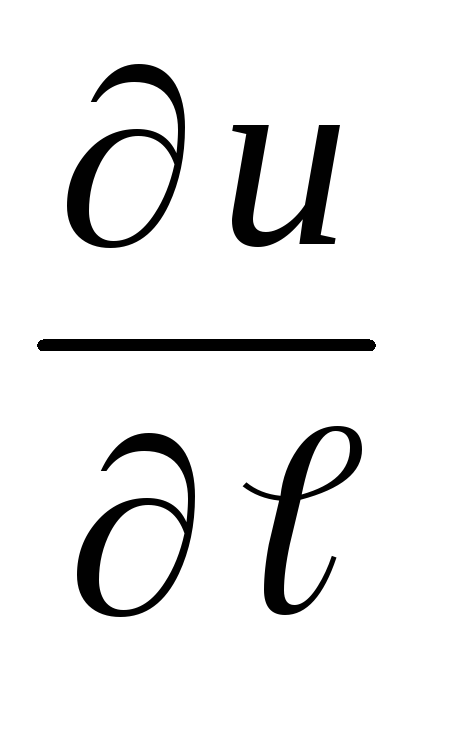 для поля
для поля
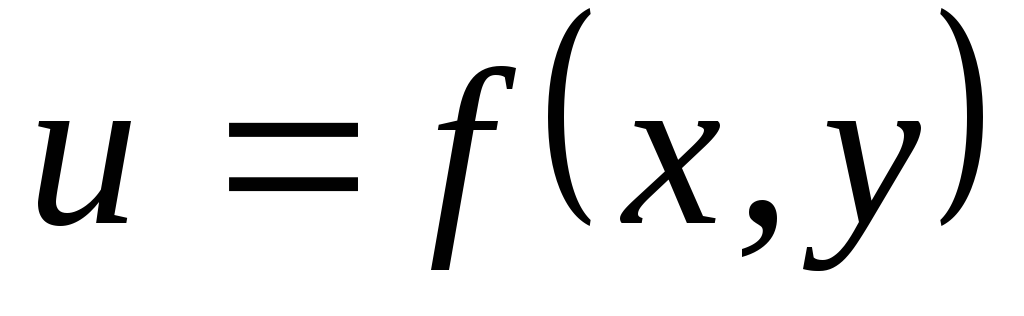 ,
заданного на плоскости, аналогичны
приведенным выше определениям 1) и 2).
,
заданного на плоскости, аналогичны
приведенным выше определениям 1) и 2).
Найти
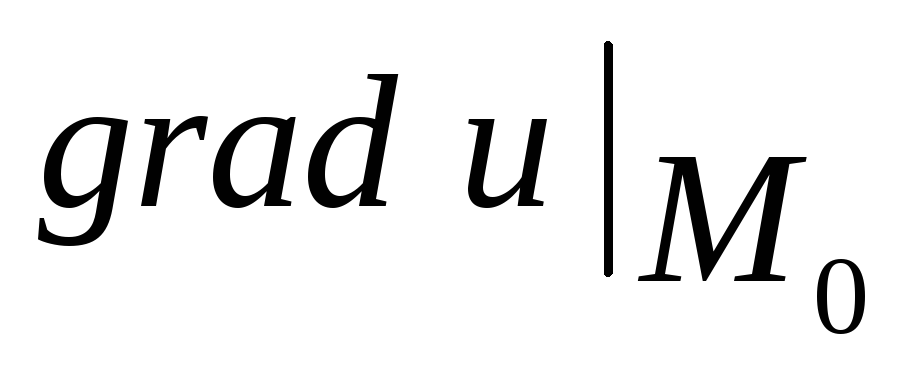 и
и 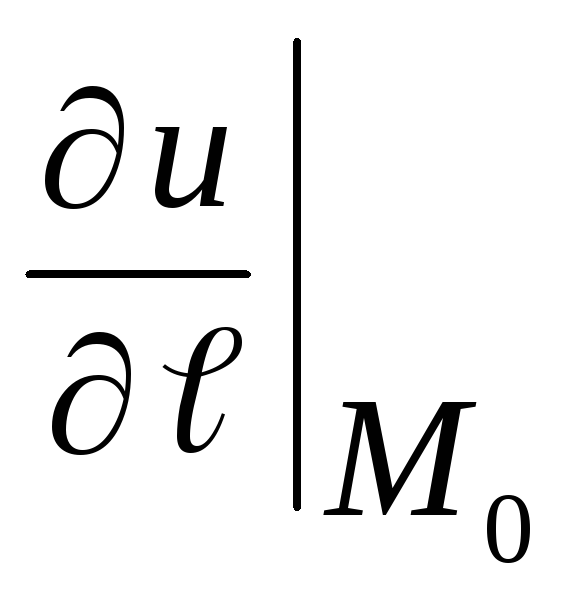 ,
если
,
если
![]() ,
,
![]() ,
,![]() .
.
Имеем:
![]() ;
;
![]() ;
;
![]() .
.
Поэтому
![]() .
.
Найдем орт
![]() вектора
вектора![]() :
:
![]() .
.
Найдем
![]() как скалярное произведение векторов
как скалярное произведение векторов![]() и
и![]() :
:
![]() .
.
Задачи для самостоятельного решения
Найти экстремумы функций:
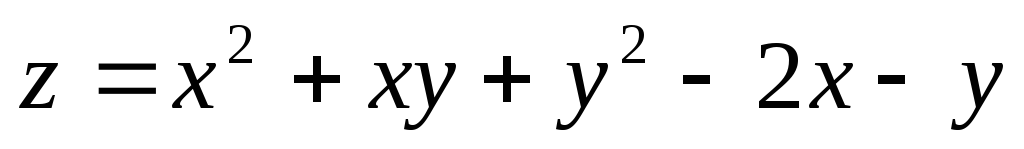 ;
;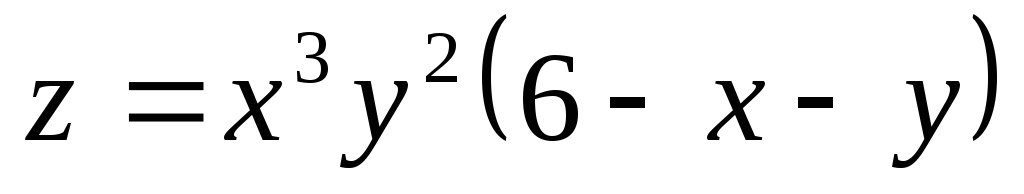 ;
;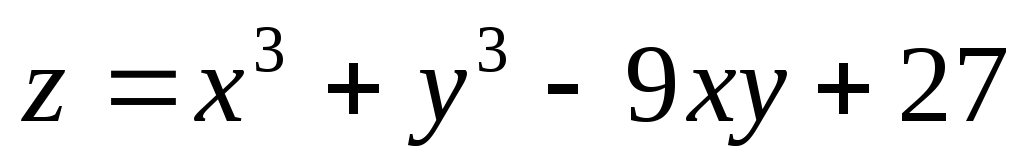 ;
;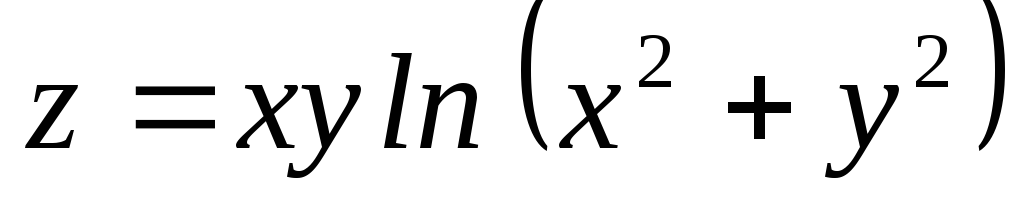 ;
;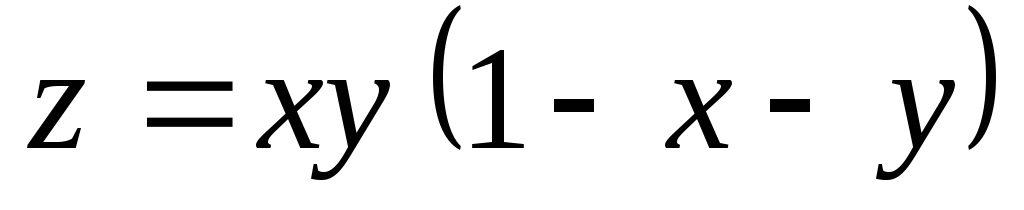 ;
;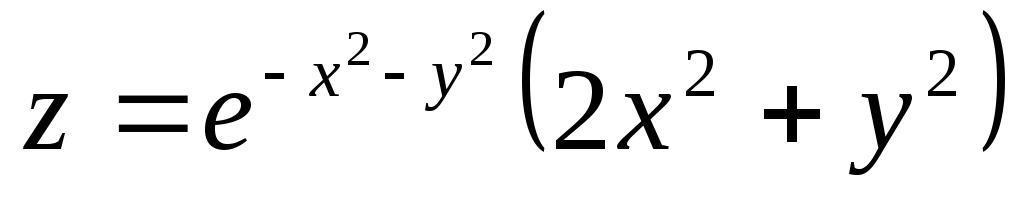 ;
;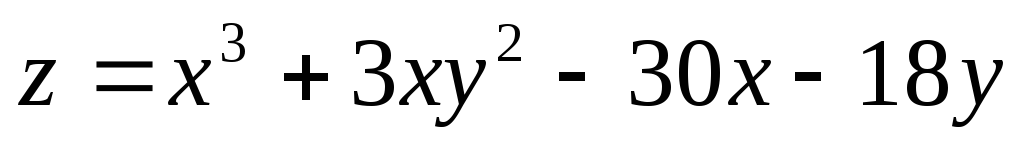 ;
;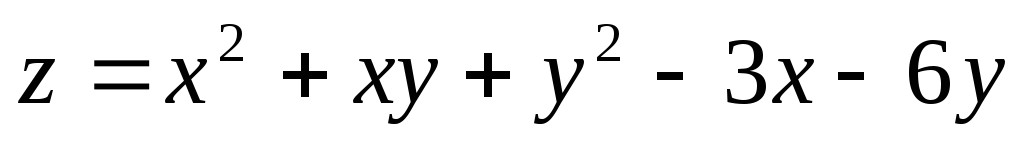 ;
;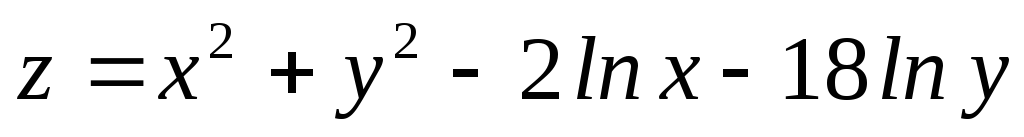
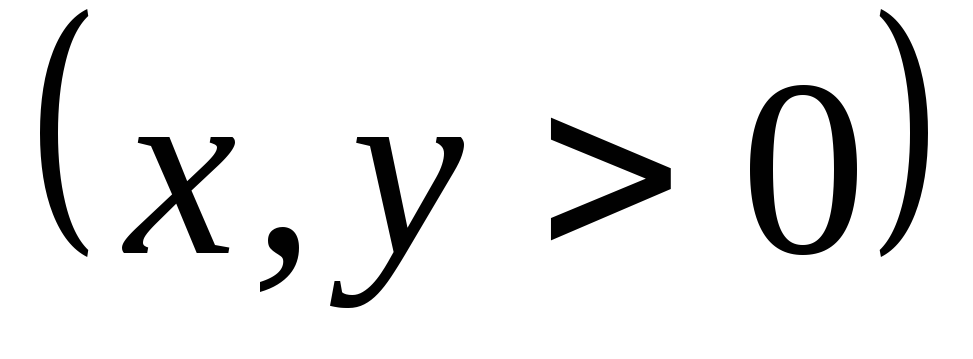 .
.
При каких
![]() функция
функция
имеет максимум (минимум)?
Найти наибольшее и наименьшее значение
функции
![]() .
в заданной области
.
в заданной области![]() :
:
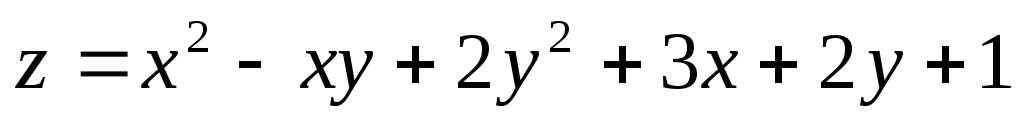 ;
;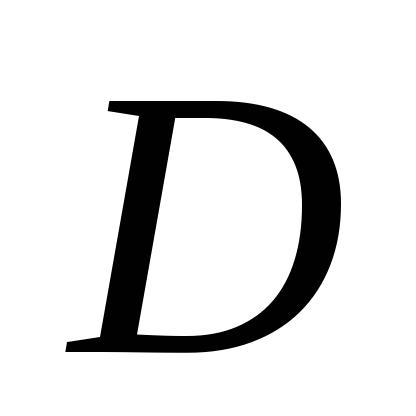 – треугольник, ограниченный прямыми
– треугольник, ограниченный прямыми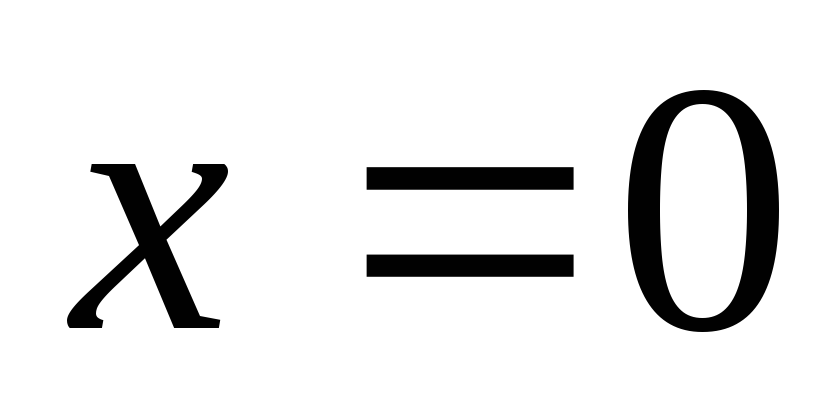 ,
,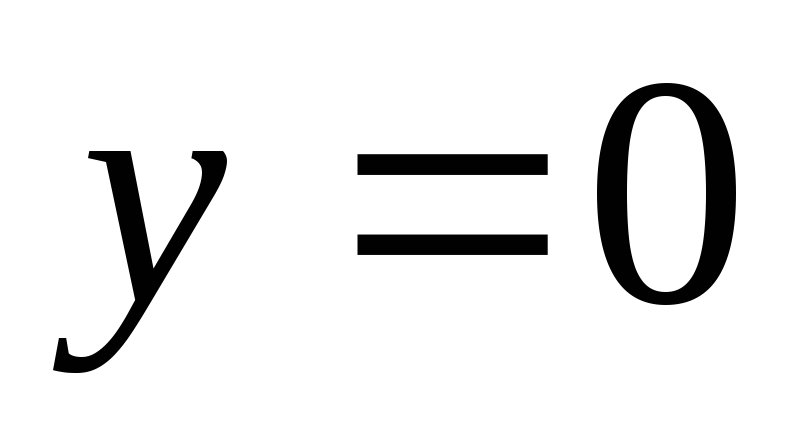 ,
, .
.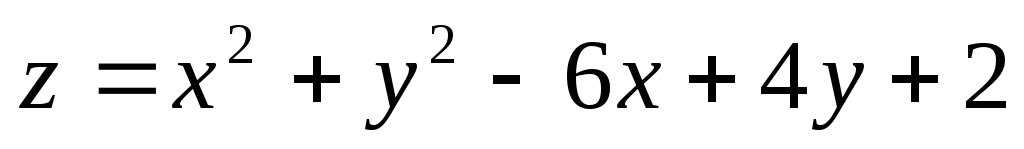 ;
;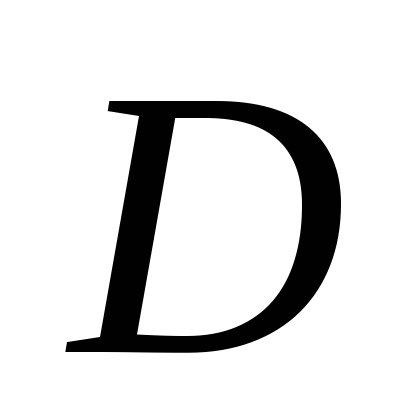 – прямоугольник с вершинами
– прямоугольник с вершинами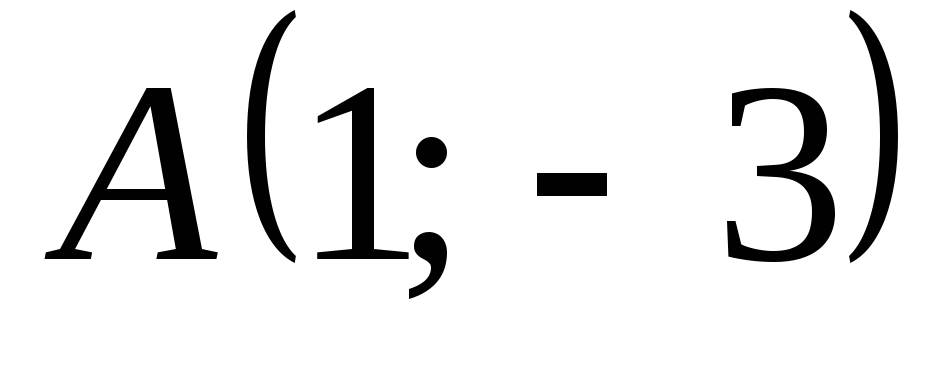 ,
,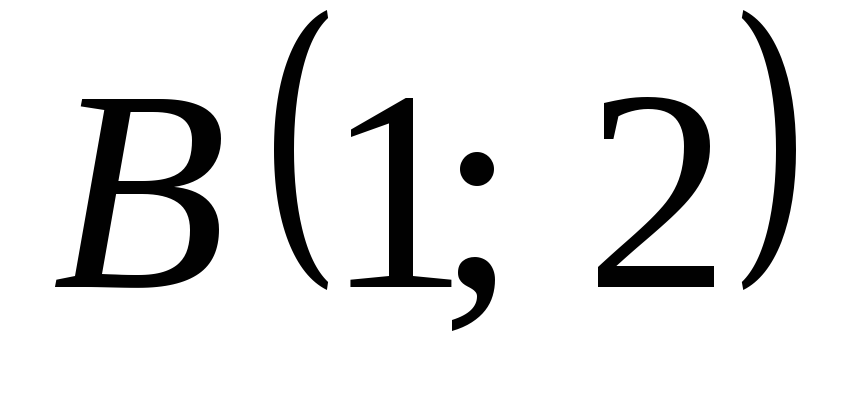 ,
,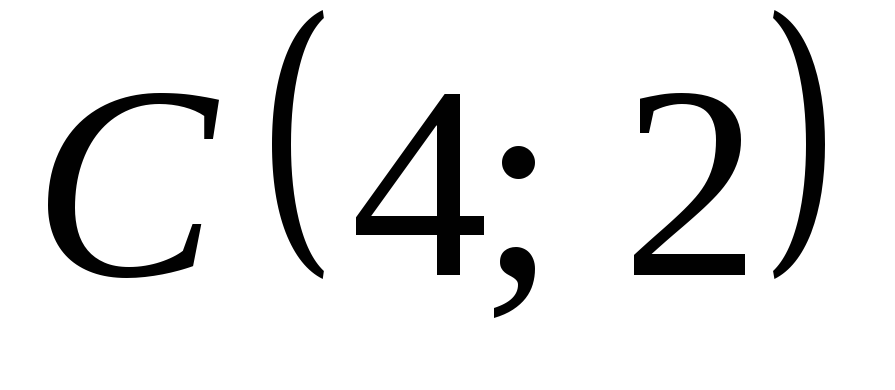 ,
,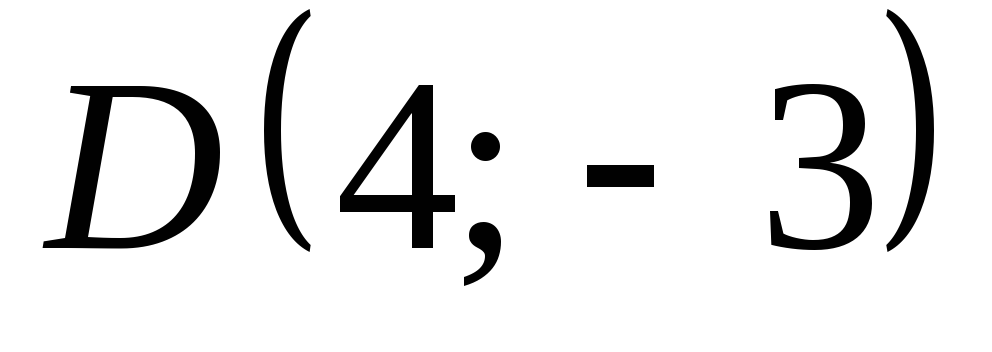 .
. ;
; – круг с центром в точке
– круг с центром в точке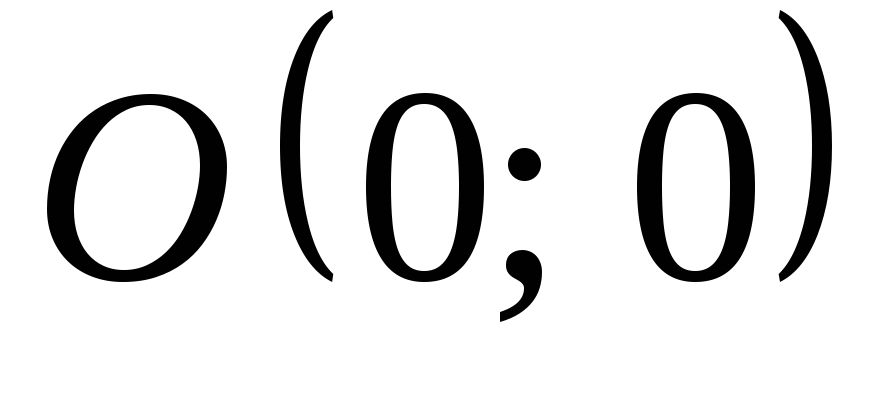 радиуса
радиуса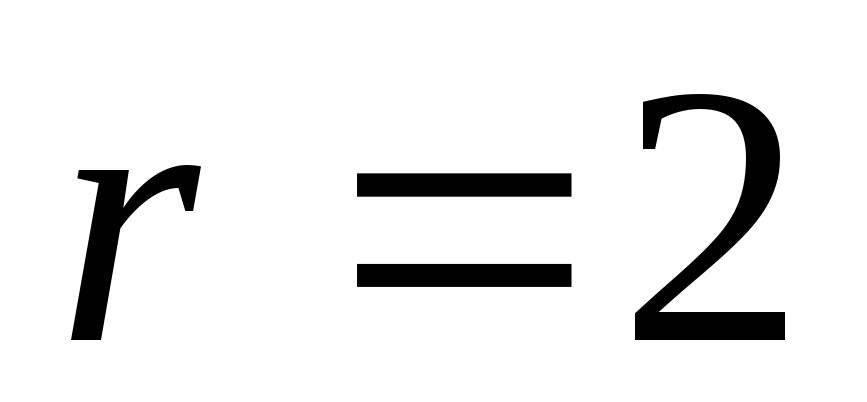 .
.
Найти
![]() и
и ![]() для
заданного поля
для
заданного поля![]() ,
точки
,
точки![]() и вектора
и вектора![]() :
:
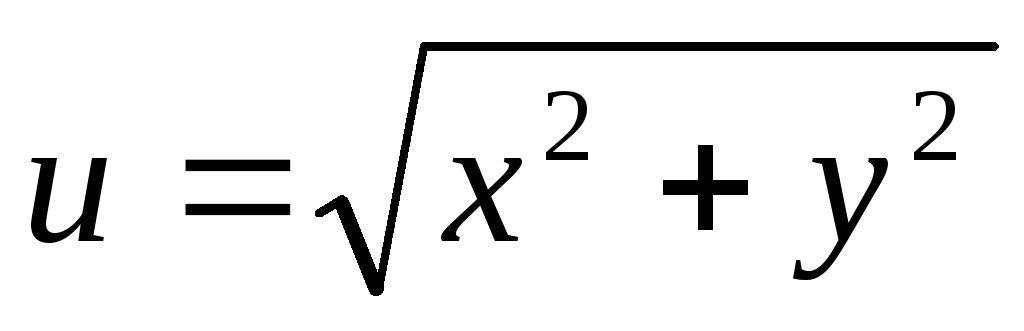 ,
,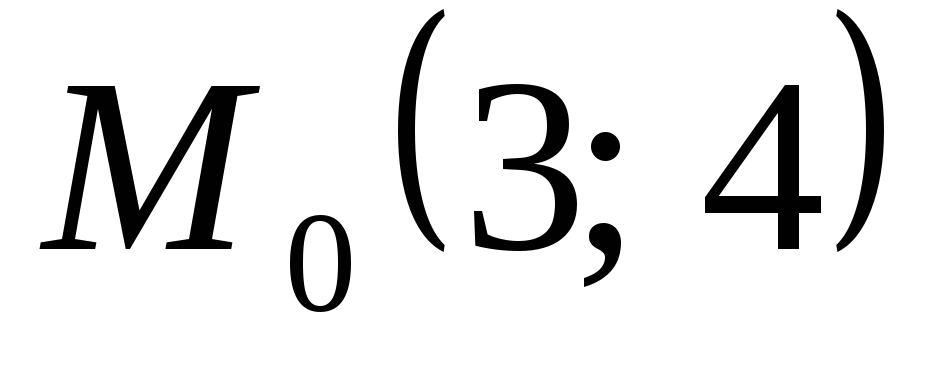 ,
,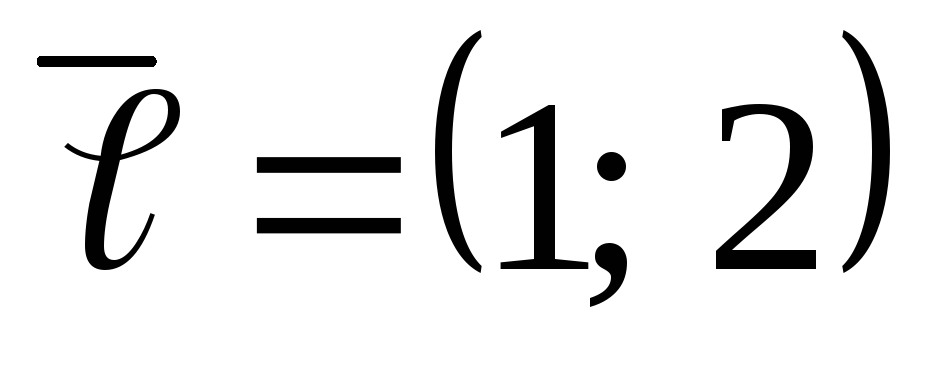 .
.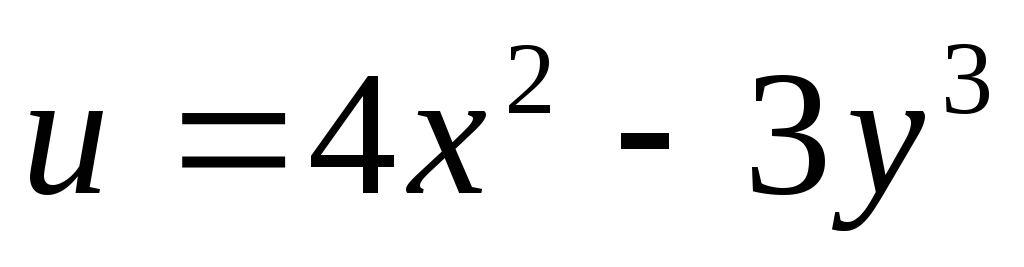 ,
,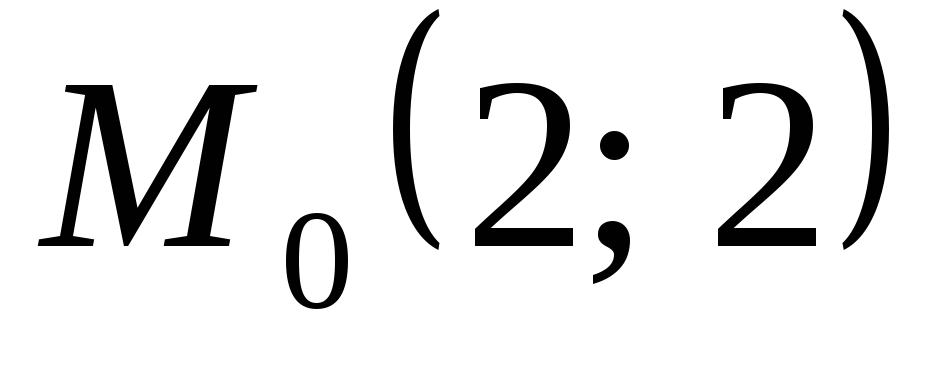 ,
,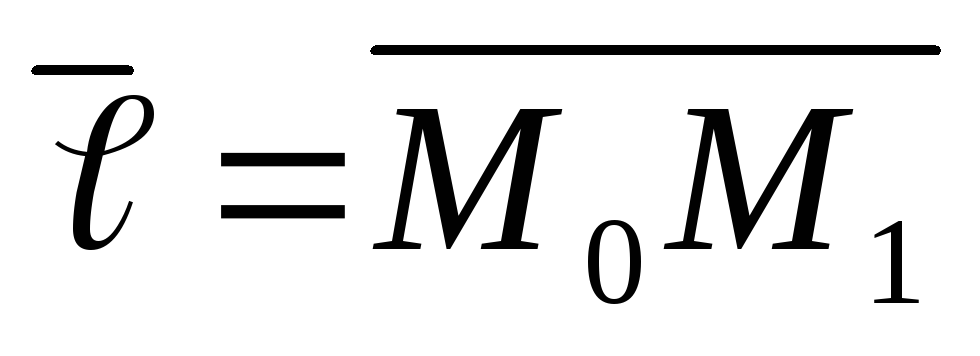 ,
,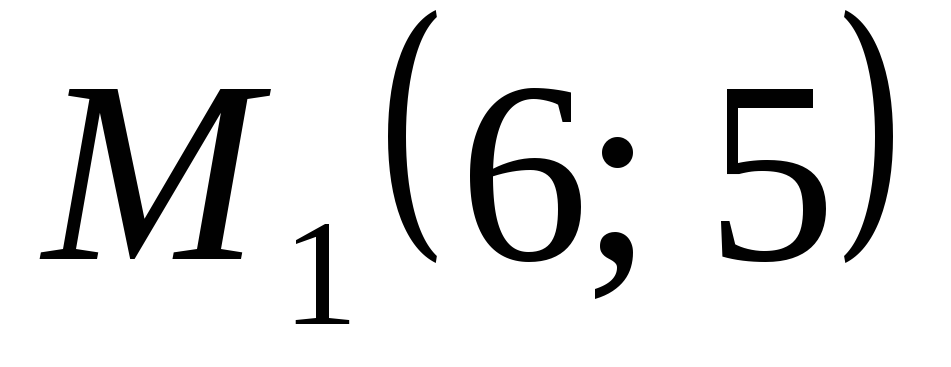 .
. ,
,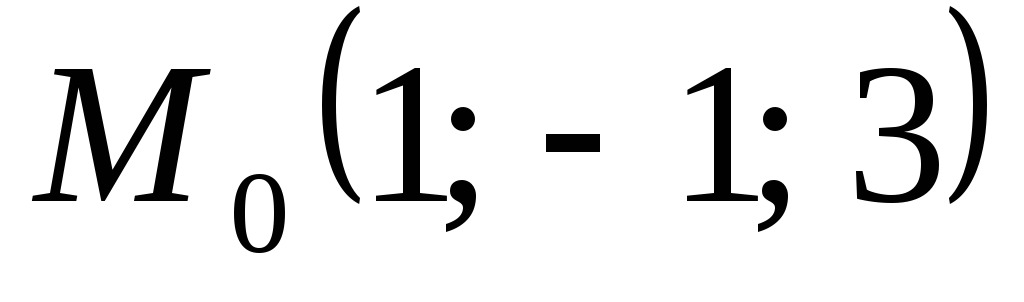 ,
,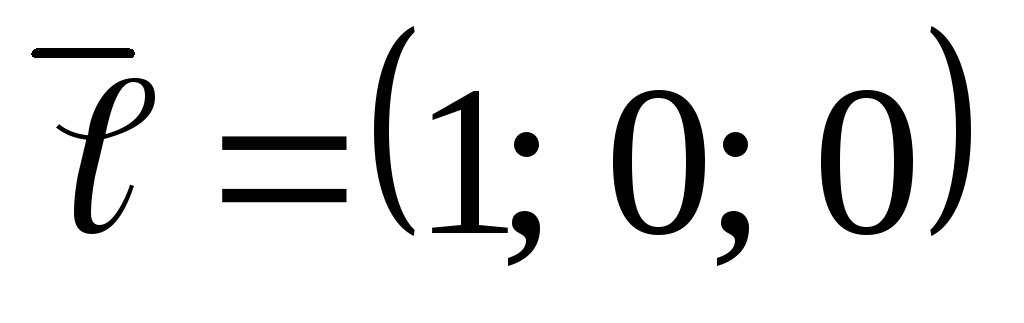 .
.
Занятие 16. Контрольная работа №3 по теме «Дифференциальное исчисление функций двух переменных». Вариант-образец.
Найти
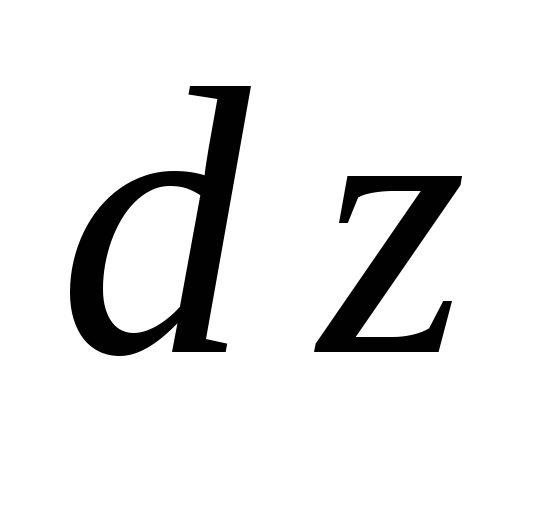 для функции
для функции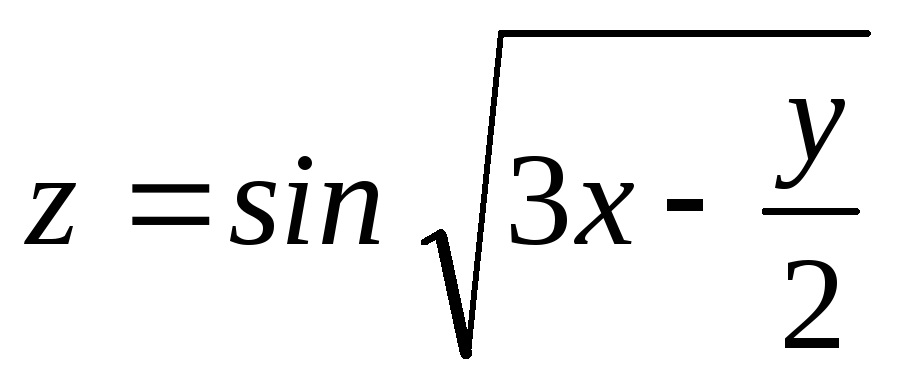 .
.
Решение.
Найдем
![]() и
и![]() :
:
![]() ;
;
![]() .
.
Поэтому
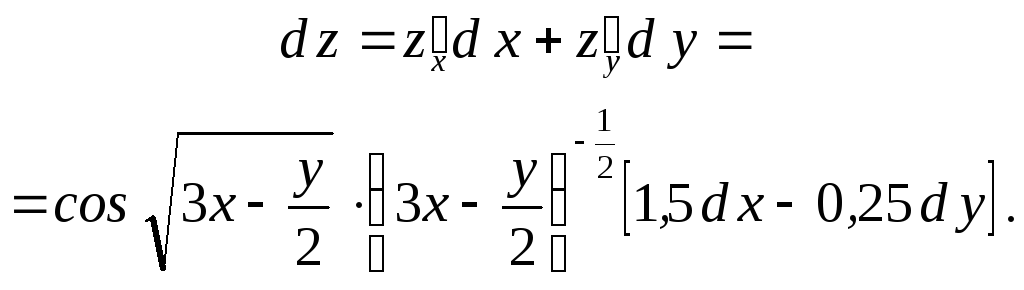
Найти
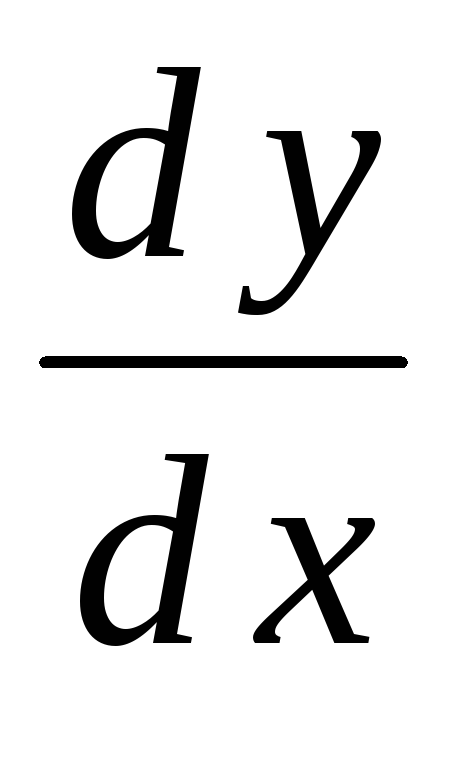 для функции
для функции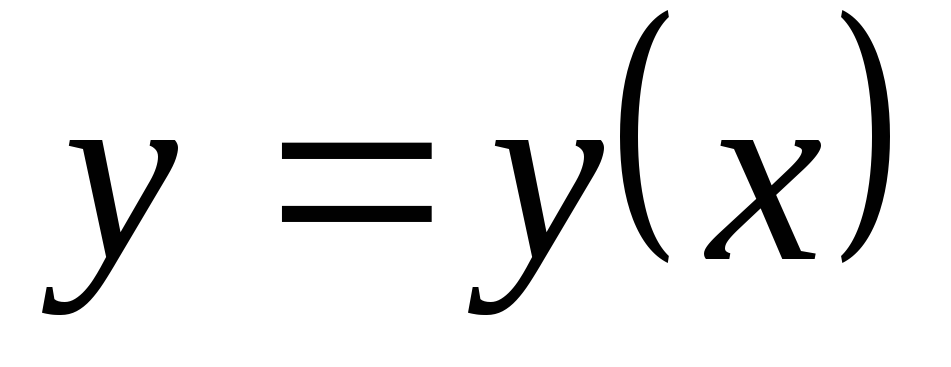 ,
заданной неявно уравнением
,
заданной неявно уравнением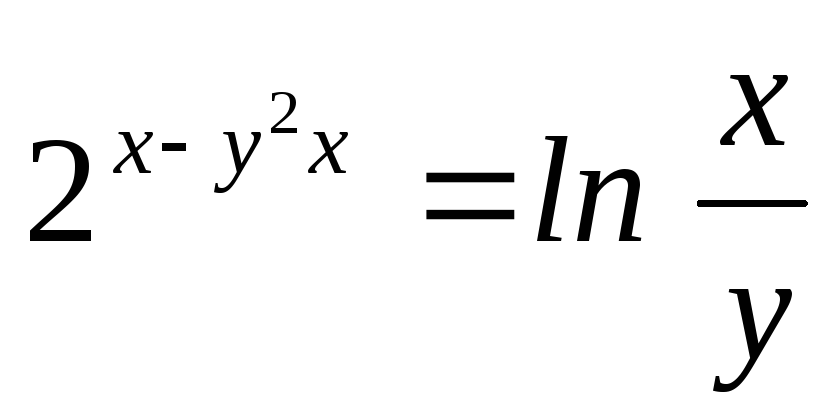 .
.
Решение.
Имеем:
![]() .
.
Найдем
![]() и
и![]() :
:
![]() ;
;
![]() .
.
Поэтому:
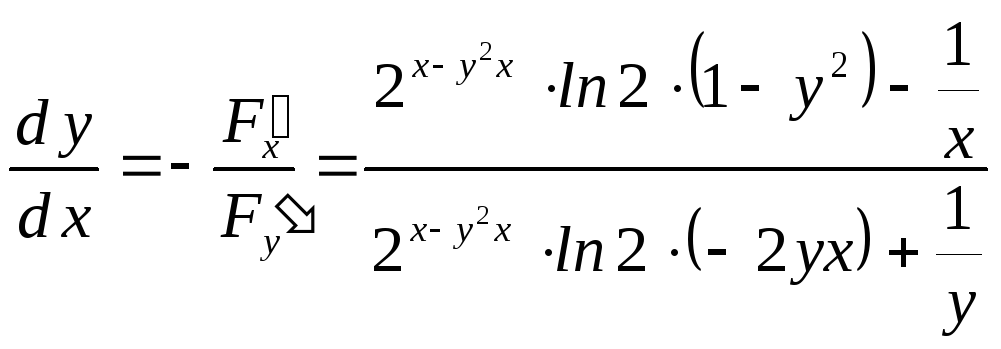 .
.
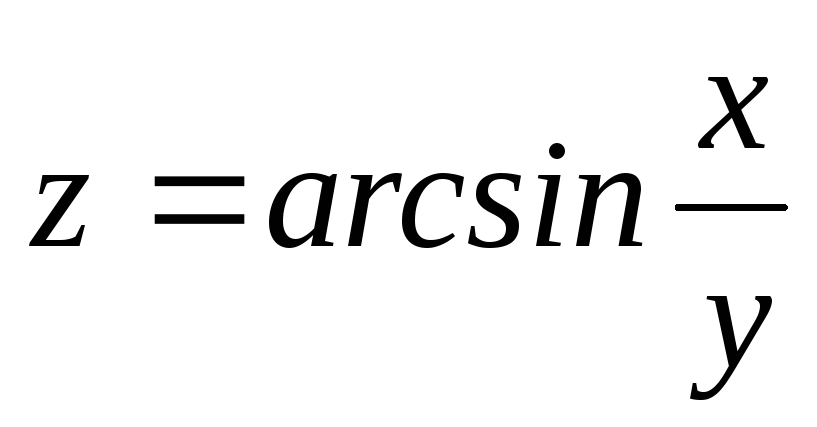 ,
а
,
а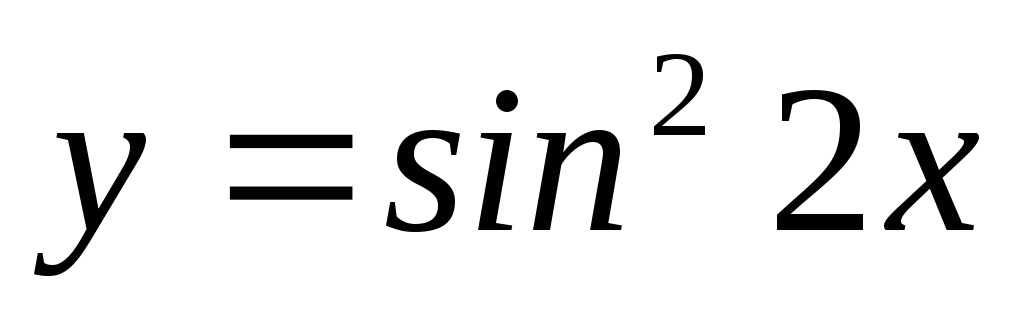 .
Найти
.
Найти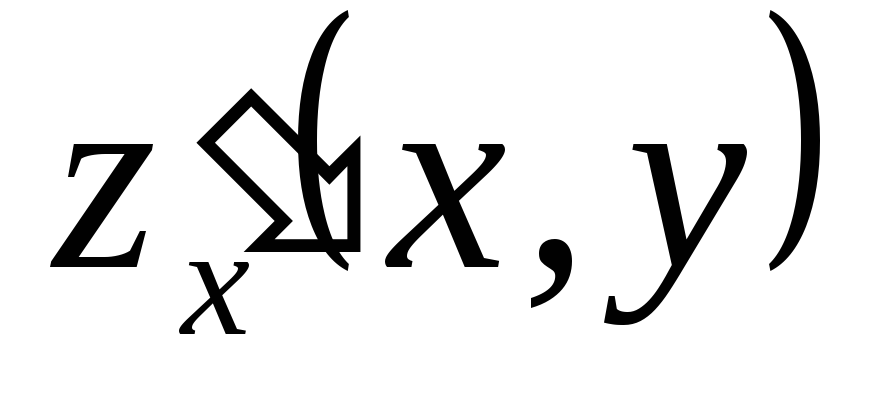 и
и ,
используя формулу для производной
сложной функции.
,
используя формулу для производной
сложной функции.
Решение.
Имеем:
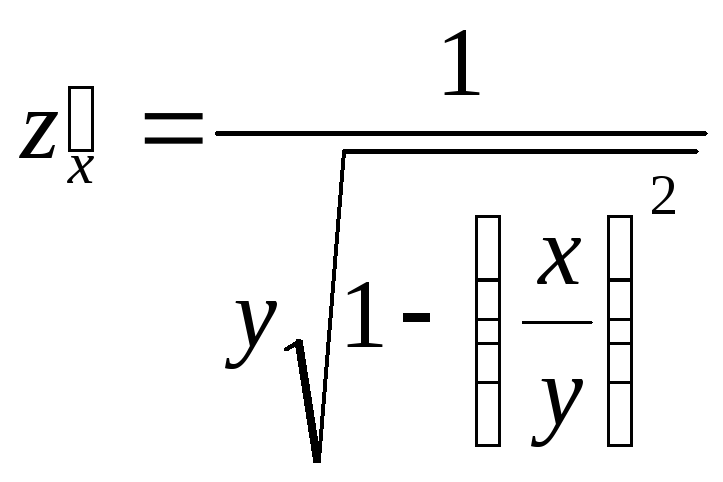 ,
,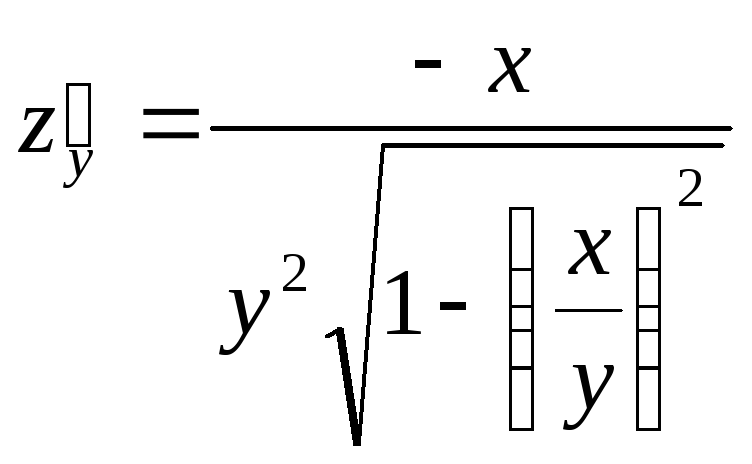 ,
,![]() .
.
Так как
![]() ,
,
то:
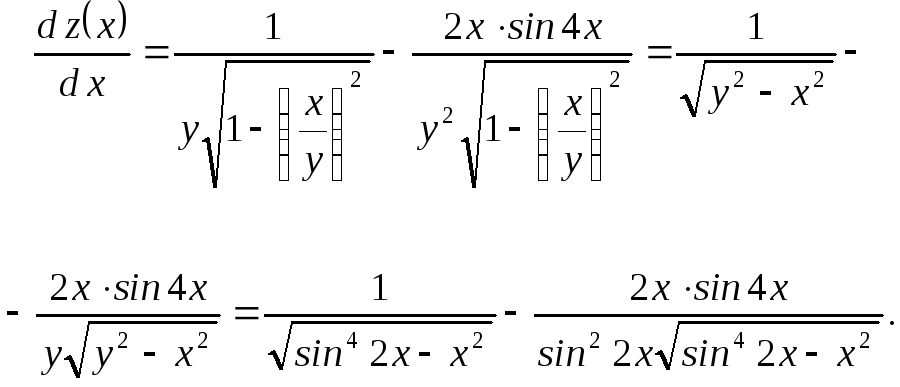
Пусть
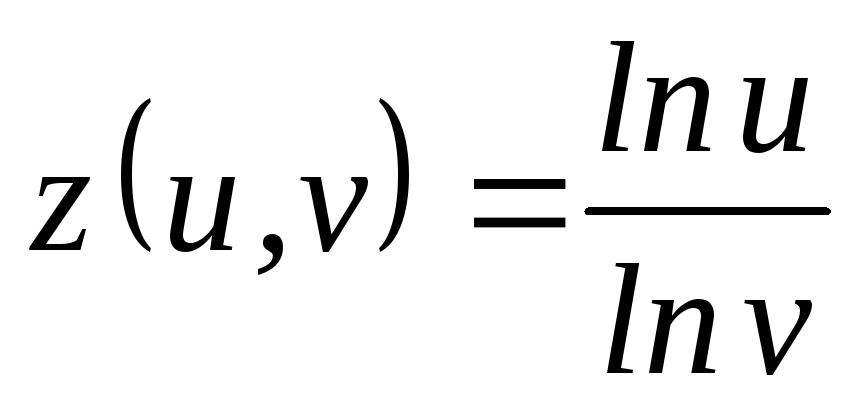 ,
, ,
,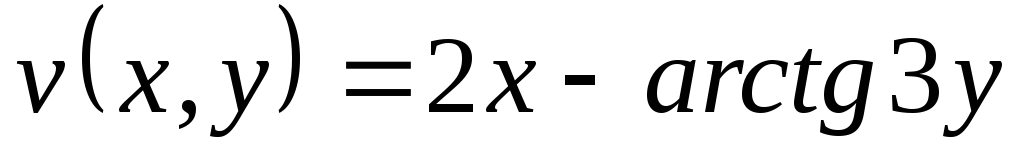 .
Найти
.
Найти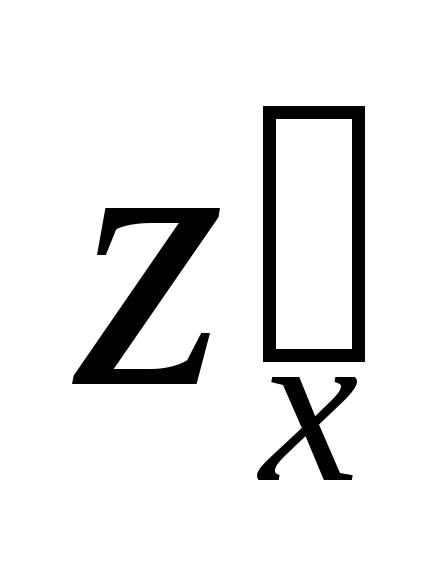 ,
,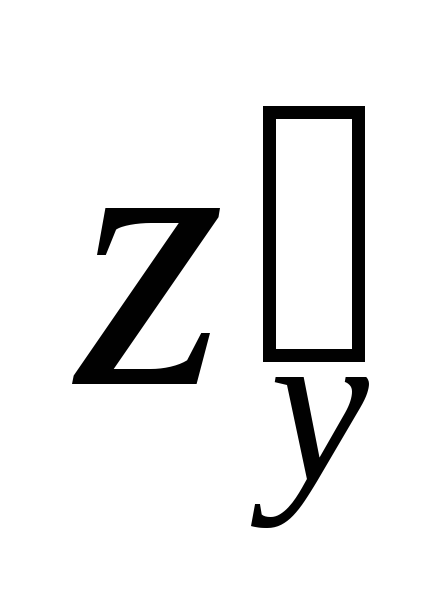 ,
используя формулы для частных производных
сложной функции:
,
используя формулы для частных производных
сложной функции:
Решение.
Найдем 6 частных производных:
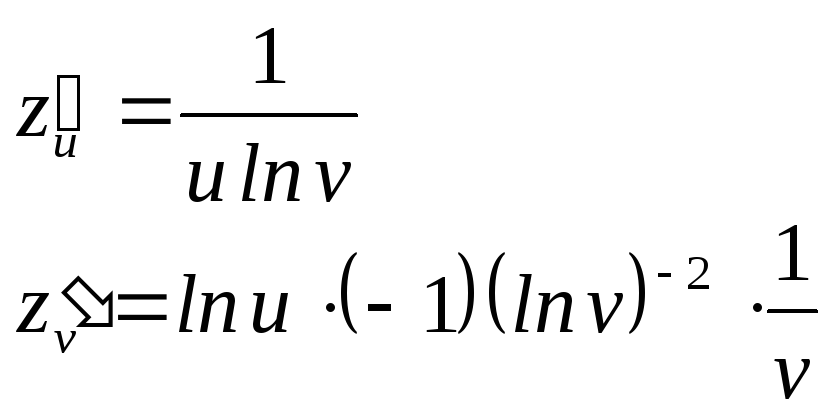
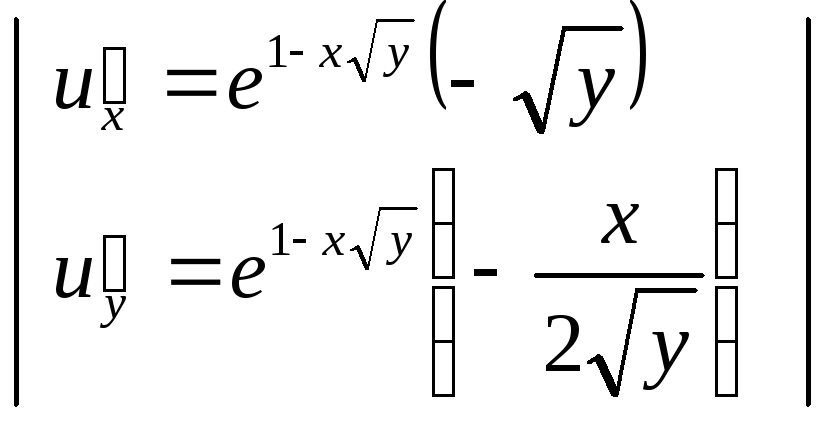
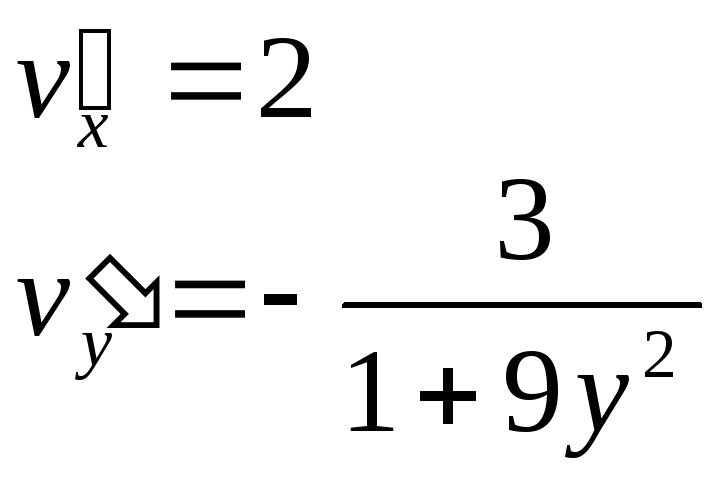
Используем формулы:
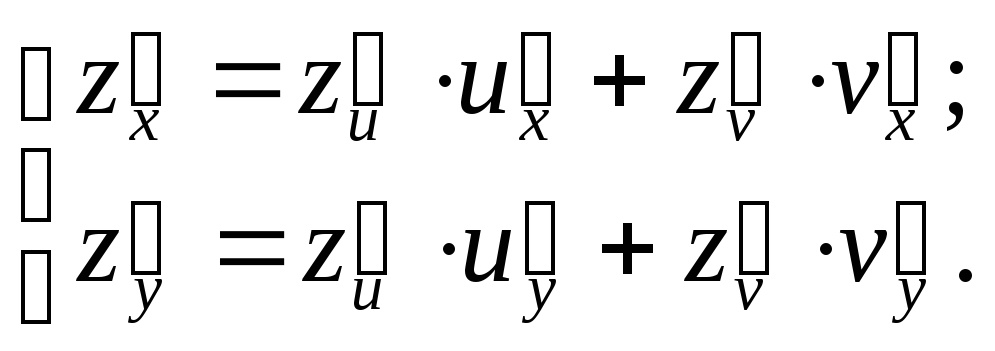
Получаем:
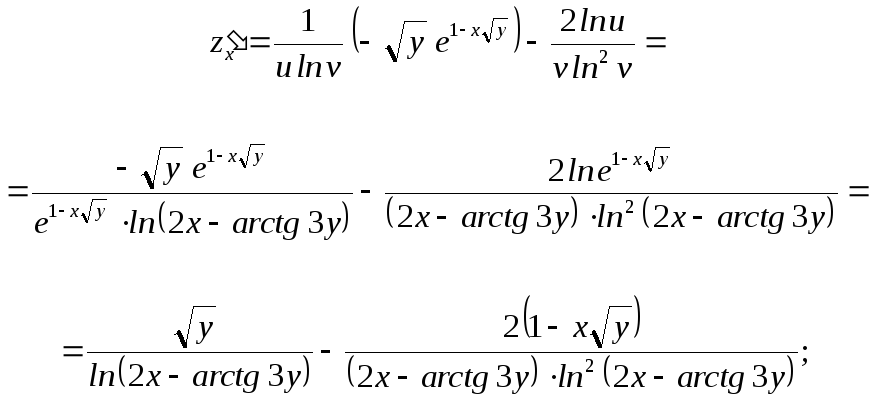
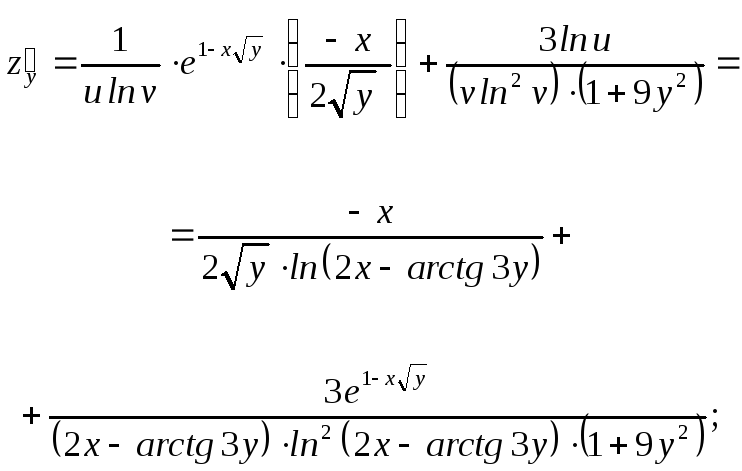
Исследовать на экстремум функцию
![]() .
.
Решение.
Найдем все частные производные функции
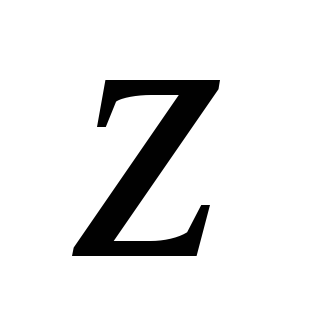 до второго порядка включительно:
до второго порядка включительно:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Найдем стационарные точки
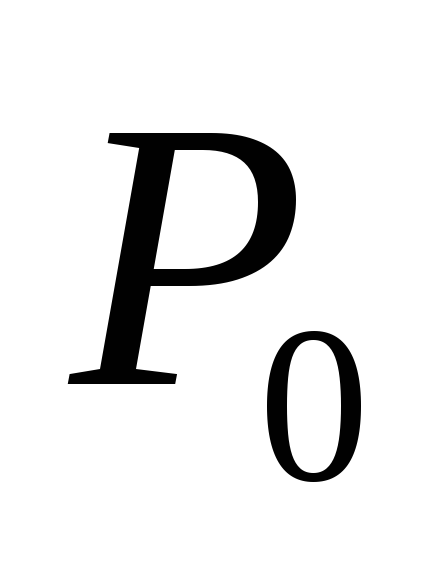 :
:
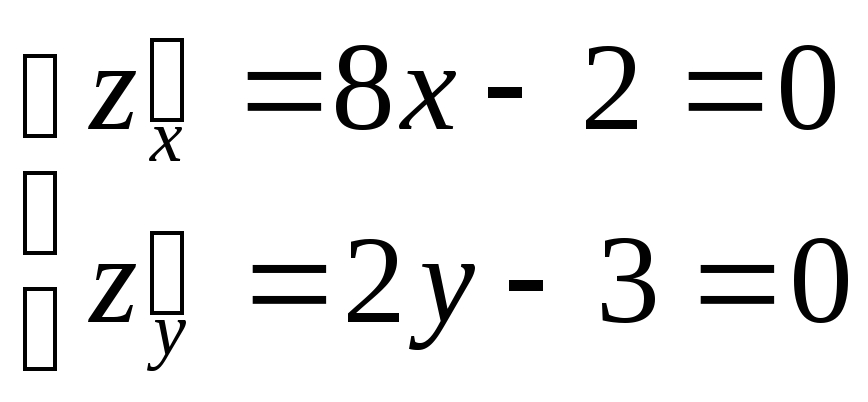
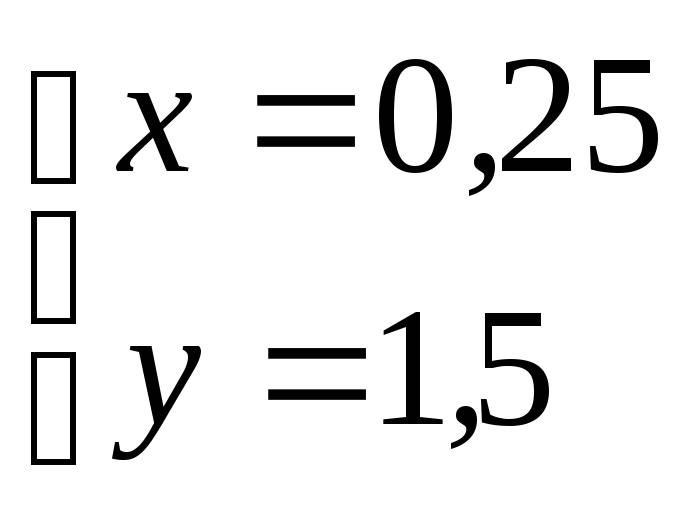
![]() – стационарная точка
– стационарная точка
Составим
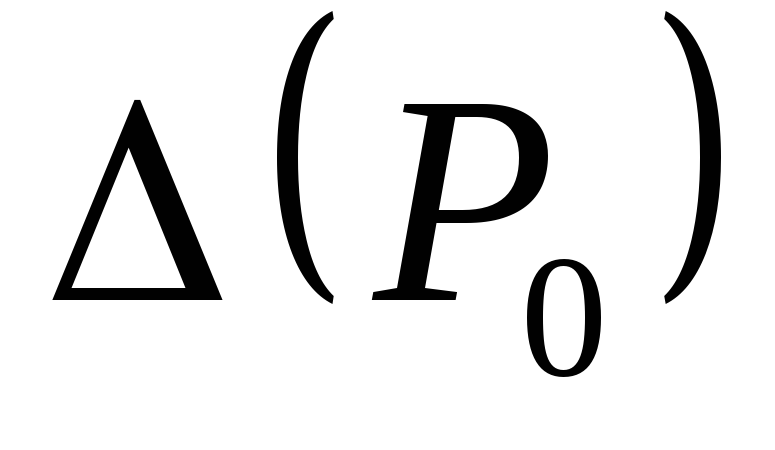 :
:
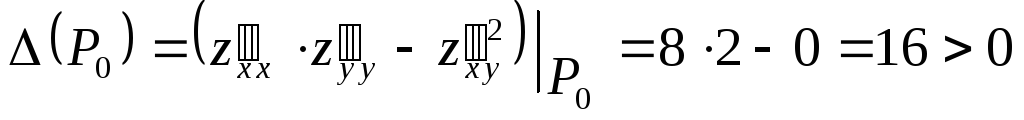 .
.
Следовательно, в точке
![]() есть экстремум.
есть экстремум.
Определим знак
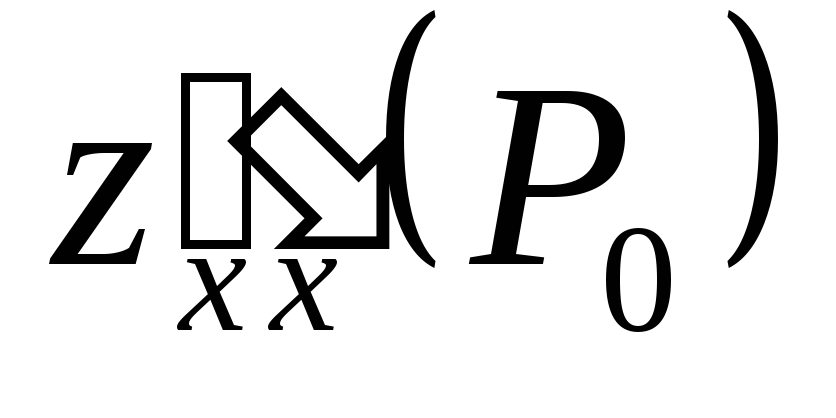 :
: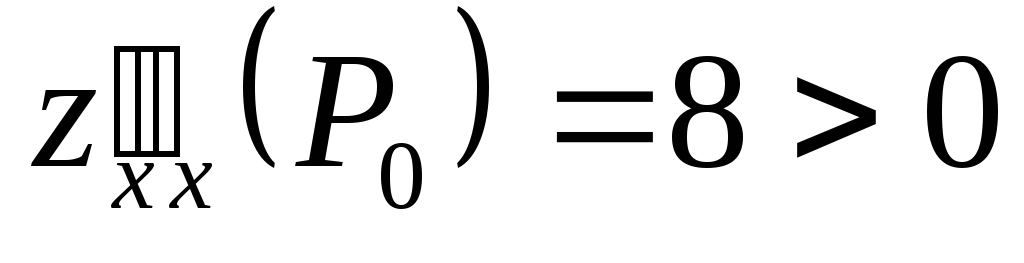 .
.
Следовательно,
![]() – точка минимума, и
– точка минимума, и
![]() .
.
Ответ: ![]() – точка минимума,
– точка минимума,![]() .
.
Занятие 17. Метод наименьших квадратов для обработки результатов эксперимента
В естествознании, технике и экономике часто приходится иметь дело с эмпирическими формулами, т.е. формулами, составленными на основе обработки статистических данных или результатов опытов. Одним из широко распространенных приемов построения таких формул являетсяметод наименьших квадратов. Изложим кратко идею этого метода.
Пусть требуется установить зависимость
между двумя величинами
![]() и
и![]() ,
например, между стоимостью потребляемого
сырья и стоимостью выпущенной продукции.
,
например, между стоимостью потребляемого
сырья и стоимостью выпущенной продукции.
Произведем обследование
![]() видов продукции и представим результаты
исследования в виде таблицы:
видов продукции и представим результаты
исследования в виде таблицы:
|
|
|
|
|
|
|
|
|
|
|
|
Изобразим на координатной плоскости
![]() точки
точки![]() с координатами
с координатами![]()
![]() .
Предположим, что эти точки располагаются
на плоскости около некоторой прямой
линии (см. рис.5). Это означает, что между
переменными величинами
.
Предположим, что эти точки располагаются
на плоскости около некоторой прямой
линии (см. рис.5). Это означает, что между
переменными величинами![]() и
и![]() существует приближенная линейная
зависимость вида
существует приближенная линейная
зависимость вида
![]()
при некоторых
![]() и
и![]() .
.
Для нахождения
![]() ,
,![]() применяютметод наименьших квадратов,
позволяющий получить оптимальную (в
некотором смысле) прямую.
применяютметод наименьших квадратов,
позволяющий получить оптимальную (в
некотором смысле) прямую.

Обозначим yi*=axi+b
(i=1,…,n)– значения переменной![]() ,
получаемые при помощи уравнения
,
получаемые при помощи уравнения![]() .
Обозначим
.
Обозначим
![]() .
.
Величина
![]() показывает отклонение расчетного
значения переменной
показывает отклонение расчетного
значения переменной![]() (т.е.
(т.е.![]() )
от экспериментального (т.е. от
)
от экспериментального (т.е. от![]() ).
).
Метод наименьших квадратов
подбора![]() и
и![]() заключается в том, что эти параметры
выбираются из условия: сумма
заключается в том, что эти параметры
выбираются из условия: сумма![]() – минимальна.
– минимальна.
Запишем выражение для
![]() ,
учитывая формулы для
,
учитывая формулы для![]() :
:
![]()
Выберем значения
![]() и
и![]() так, чтобы функция двух переменныхu=
так, чтобы функция двух переменныхu=![]() имела бы в соответствующей точке минимум.
Напомним необходимое условие экстремума:
имела бы в соответствующей точке минимум.
Напомним необходимое условие экстремума:
![]() ,
,![]() .
.
Имеем:
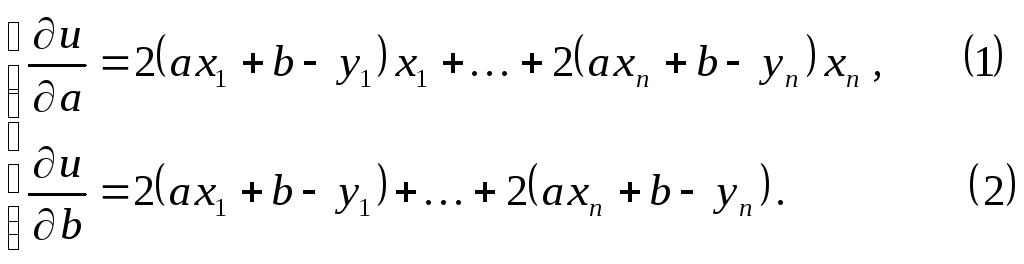
Получаем систему уравнений:
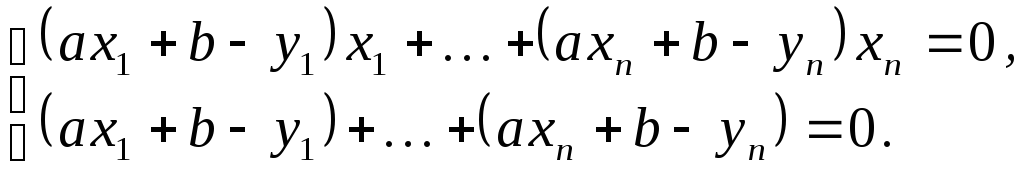
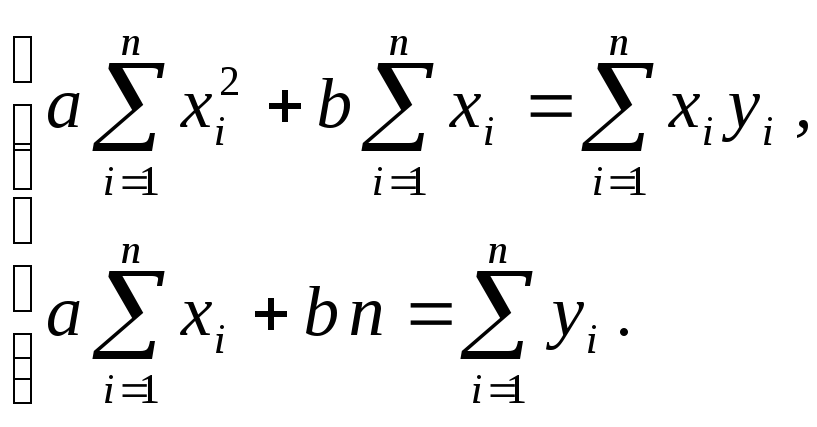
Решив эту систему уравнений, находим
![]() и
и![]() ,
и затем подставляем их в эмпирическую
формулу
,
и затем подставляем их в эмпирическую
формулу![]() .
.
Предположим теперь, что точки на плоскости
располагаются вблизи некоторой параболы,
т. е.
![]() приближенно зависит от
приближенно зависит от![]() следующим образом:
следующим образом:
![]()
Тогда:
![]() ,
,![]() ,
,![]() ,
,

Здесь
![]() – функция трех переменных
– функция трех переменных![]() ,
,![]() ,
,![]() .
.
Необходимые условия экстремума
![]() ,
,![]() ,
,![]()
в этом случае принимают следующий вид:
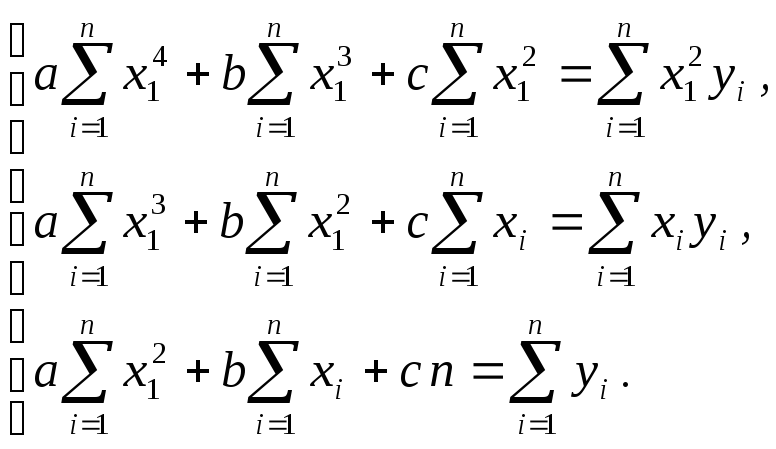
Решая полученную систему уравнений
относительно
![]() ,
,![]() ,
,
![]() ,
затем построим и само уравнение
,
затем построим и само уравнение![]() .
.
Пример 1. Темпы роста
производительности труда
![]() по годам
по годам![]() в промышленности республики приведены
в таблице, данной ниже. Предполагая, что
в промышленности республики приведены
в таблице, данной ниже. Предполагая, что![]() ,
найти
,
найти![]() и
и![]() .
.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
100 |
156 |
170 |
184 |
194 |
205 |
220 |
229 |
Составим систему уравнений для определения aи b. Для этого сначала найдем следующие величины:
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Таким образом, имеем следующую систему уравнений относительно aиb:
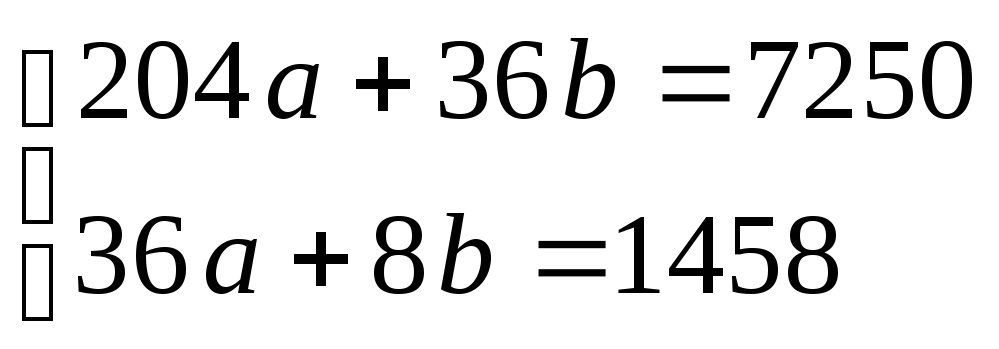 ,
,
решая которую, получим:
![]() ;
;![]() .
.
Итак, уравнение искомой прямой:
![]() .
.
