1031

Внyrpи h)- не имеют смысла понятия макромеханики, Т.е.

«координата»j «скорость» и другие. Как это можно понять? Что значит, точно знать координату и ИМПУЛЬС (или скорость)? В классической физике - это значит, в каждый момент времени иметь ВОЗМОЖНОСТЬ замсрить

скорость и зафиксировать положение 'Тсла.

Можно ЛИ зто сделать д,lЯ микрочастицы, например электрона в атоме? Для этого нужно <<Осветить» электрон светом, длина волны

которого соизмерима с размером хотя бы атома ..... 10·8 СМ (это частота рентгеновских лучей). Энергия кванта

hc	6.62 ·\0-27 ·3·\010	20 . \ О -9	эрг
Е ~ h v ~ ~ ~	\ О -,
А.

или 6,62 ·\0-34 .3.\0'

20 -\0 -16 Дж

\ О -10

Потенциал ионизации атома водорода 10:= 20 ·10-12 эр? = 20 ·10-19 Дж, т.е.

на три порядка меньше энергии кванта рентгеновских лучей.

Значит, освещение атома длинной волны ..... 10-1 см приведет к тому,

ЧТО электрон будет выбит из атома, и о его состоянии (его импульсе) мы

ничего сказать не можем. Т. е. соотношение нсопределеНJIОСТИ, зто не

результат того, что мы не можем создать точный прибор и все измерить.

Это связано с прирадой частиц, это особенность микромира.

Если МЫ хотим одновременно измерить Е и t (время), когда электрон (или фотон) имеет эту энсрrnю, то точность этих измерений тоже

ограничена принципом неопределенности в таком виде: М· ы > h .

Огромная заслуга в установлении общих принципов описания

явлений микромира принадлежит Нильсу Бору. Бор сформулировал знаменитый npинцun доnолнumельносmu, который включает в себя особенности постановки задачи О наблюдении. «ДОПОJIнительность

характеризует новую СИ'"fуацию в отношении описания физических

явлений - нельзя точно определить две взаимно дополнительные физические величинЫ». При этом Бор писал, что «как бы далеко не выходили явления за рамки классического физическOI'О объяснения вес

опытные Данные должны описываться при помощи классических

понятию).

Итак, в первой трети 20 столетия усилиями целой плеяды блестящих

физиков создание квантовой механики, которая по праву считается

основой всей современной физики, было завершено.

12

http://mitht.ru/e-library

Существуют разные методы построения квантовой механики. Они

отличаются друг от друга различной сложностью математического

аппарата. Самый распространенный метоД - зто метод Шредингера. Он

наиболее прост в математическом отношении и мы будем пользоваться тоже именно этим методом квантовой механики, Основы квантовой

механики принято представлять в виде совокупности ряда постулатов или

положений.

1.2. Постулаты квантовой механики

Постулат 1

Систему частиц МОЖНО характеризовать функцией 0/ (q J, ••• Qnt), которая называется волновой функцией, и через которую определяются все

измеримые величины ДЛЯ системы ИЗ n частиц, где q ~ пространственные

координаты и t - время. для стационарных систем tp является функцией

только координат.

Физический смысл имеет произведение 'р. 'Р' ·dт(чаще пишут 'fI''Vdr), эта величина определяет вероятность нахождения координат

частиц в объеме dT. Такую интерпретацию дал Борн. А поскольку каждая

частица обязательно должна быть в какой-то точке пространства, то

интегрирование по всему Зn-мсрному пространству дает:

f'J1*'J1dT=1

Т.С. достоверность

Это условие называется нормировкой. ЧJ * - комплексно-сопряженная волновая функция. Дело в том, ЧТО волновую функцию часто удобно

выражать в виде комплексного числа			'Р = а + ib, тогда этому
комплексному	числу	соответствует	КОМIIлексно-сопряженное

Ч'* = а - ib. Произведение ЧJ''Т' всегда будет Действительное число, и

поэтому МЫ, дЛЯ упрощения будем пользоваться действительными

функциями. Итак, ЧJ''Р -= 1'+'12 - эту величину часто называют ПЛОТНОСТhЮ

вероятности координат частицы и тогда сама 'Р ~амnлитуда плотности

вероятности, а 1.fI·l.f'd. -вероятность нахождения частицы в объеме d.

Такая интерпретация 1'+'12 как плотности вероятности нахОДИТСЯ в

согласии с ОСНОВНЫМ ПРИНUИ110М кваmовой механики - принципом

неопределенности Гейзенберга. Исходя из смысла ''Р/2 •d7:, волновая

функция должна обладать рядом свойств. Она должна быть:

•однозначной

•непрерывной

•конечной

13

http://mitht.ru/e-library

Функции, удовлетворяющие ЭТИМ 1ребованиям~ называются

регулярчымu.

ПоnyлаТ2

К~ЖДОЙ физически наблюдаемой в класСической механике величине

в кваНТОвой механике сопоставляется линейный оператор.

011ераmор - зто значок (или символ), который показывает какое

деЙСТвИе нужно произвести над функцией, чтобы ПОЛУЧИТЬ новую

дЛх)

функцию. Например, когда мы функцию дифференцируем, то в дх

д

значок дх является оператором дифференцирования и тогда можно

заПисаТЬ:

ВЛх) = дЛх)		В= а
дх	,где	ах
Очень важным оператором в квантовой механике является оператор
Лапласа. который обозначается IJ.	или V	2 (набла). Этот оператор

показЫ6Зет, что от ФУНКЦИИ нужно взять сумму вторых производных по

коордиtlзтам X,Y.Z:

2	а2!		а2 !		а2 !
'11 j(x,y,z) =	ах	2	+ q;2	+	Bz	2

в квантовой механике лрименяются линейные операторы, т. е.

такие операторы, которые удовлетворяют условиям:

1. Р[[1(х) + [2 (х)]= Ff1(х) + Ff2 (х)

F[cf(x)] = cFf(x) и

FfCl~(X)+C2f2(X)]=CIF~(x)+~Ff2(X)

где J;(x) И J;(x) - произвольные ФУНКЦИИ и С( И С1 - произвольные

постоянные. Линейные операторы можно складывать и умножать:

2.Если А и В являются линейными операторами, то:

А+ В = S (Т. С. их линейная комбинация)

АВ=Р s и р тоже линейные операторы.

з. Если

сумма

двух

операторов

S = А + В.

ТО

Sf(x) =(А +В)Лх) =АЛх) + ВЛх)

Произведение р = А . В

14

http://mitht.ru/e-library

РЛх) = АВЛх) = А[ВЛх)]

в общем случае порядок расположения днух операторов в

произведении не безразличен, т. е. линейные операторы не обязательно

КОММУГИРУЮ1'. Если же А· В = В· А, то операторы обладают свойствами

коммуmаmuвносmи.

Важным СВОИСТВОМ операторов является СВОЙСТВО самосопряжеНI:IОСТИ -

поскольку операторы должны приводить к вещественным значениям

величин, то должно выполняться условие

f'f" F'I'd, "" f'f'F''f''d"

Т.е. если в операторе есть i, ТО перед НИМ меняется знак. Если в

результате применения оператора F к реryлярной функции f	получается
ВНОВЬ та же ФУНКЦИЯ, умноженная на некоторое число А., Т.е,	F· f "" ij ТО

все члены указанного класса функций называются собственными

функциями оператора F, а различные возможные значения .4,

соответствующие собственным функциям, называются собственными

значениями Этого оператора.

Как же определить какой оператор нужно сопоставить той или ИНОЙ

Динамической перемевной? Есть правило нахождения квантово­

механических опера'fОРОВ, которое состоит в следующем:

Вклассической механике все динамические величины можно

выразить в переменных р и q ,Т.е. через пространственную координату и

импульс. Если динамическая персменная является прос'гранственной

координатой q, то соответствующий ей оператор булет оператор

•

умножения Q , т.к. операuия состоит в умножснии функции на эту

координату

л

QЧ' = qЧ'

•

Q-оператор, соответствующий Ч

Потенциальной энсргии тоже сопоставляется оператор умножения на эту величину, Т.К. потенциальная энергия является функцией координат

•

V(q) - V(q). Оператор, соответствующий количеству движения или

импульса обозначается

р=-ih~ =-ih'V

Bq

и является диффере~·щиальным оператором первого порядка.

15

http://mitht.ru/e-library

Он переводит ФУНКЦИЮ '{' в -1'n iWдq' Если взЯТЬ компоненты импульс&,

то соответствующие им операторы будут:

,	д'		д,	д
Р.	= -ih дх;	Ру	= -i1l ~; Р,	= -in дZ
Операторы [Р.,pJ [Р.,Р,J и		[р"	Р,J - коммутируют между собой (также

как и операторы координаты). а операторы импульса и координаты не

коммутируют. Разность А· в-В·А= р,В] называется KOMмyraTOPOM.

Операторы коммутируют если коммутатор равен нулю (или "исчезает") .

[р.,х]= Рхх - хР. = -ih ит,Д,

Важно, ч'То две физические величины могут бьrrъ одновременно измерены, если ИХ операторы коммутируют. Пр~нцип неопределенносrи

применим к тем величинам (или "наблюдаемым"). операторы которых не

	коммутируют. Кинетическая энерrnя ,	р'
	Т= mv
	2	2т

Составляющие кинетической, энергии ПО координатным осям

т	= Р,	т =	р'
•	2т		у
		у	2т

Операторы, соответствующие компонентам кинетических энергий 8

направлении трех осей:

				/;'	д'
,	11'			2т ах'
		д'	,	n'	д'
Т = ---:-..-			Т,	2т &'
,	2т ду'
Оператор кинетической энергии:
Т=- п' (д2		+ д'-+ д' )=_ п' ,,' =_ п' А
2т	ах'	0/' дZ'		2т	2т

Полная энергия классической системы равна сумме кинетической и потенциальной энергий:

,

Оператор полиои энергии или оператор Гамильтона Н

определяется как сумма операторов кинетической и потенциальной

энергий:

,	11'	( д'	д2		д')	+v,	п2	,	+v,
Н=-	2т	---+ -+-					=--У'
I		дх2	ду2	az 2		(x,y..t)	2т		(х,у.• )
					16

http://mitht.ru/e-library

С этим оператором мы будем работать в будущем.

н" - самосопря:женный линейный оператор; при ЭТОМ, поскольку он не

содержит"i ", то iJ == Н· и значит

f'l" lWdr '"f'l'lW'dr

Постулат 3

в общем виде этот ПОС1)'лат утверждает, что если волновая функция

't' есть собственная функция оператора F • то можно написать уравнение:

t'l' о .1'1'

где ..t - ССТЬ собственное значение оператора fr .

Собственные ФУНКЦИИ и соБС1"венные значения самосопряженных операторов обладают следующими важными свойствами:

1. Собственные функции любого самосопряженного оператора,

принадлежащие различным собственным значениям - ортоfOПальны

между собой во всем интервале изменения переменных:

f\}1n \}1m dr =0

2. Если одному собственному значению опсратора COOTI3CTcTByeT

несколько ра1ЛИЧНЫХ линсйно-нсзависимых собственных функций, то

функции назывютсяя вырожденlIыи•.

Если в качестве	"	взять OIlepaTOp полной энергии Н". ТО для
	F

стационарных систем (т.е. систем для которых энергия не ИЗМСJ{Яется во

времени) можно записать:

н•'l' = ЕЧ'

где Е - ПОлная энергия системы в данном состоянии - постоянная

величина (не зависящая от координат и времени).

Это и ССТЬ уравнение Шредингера в операторной форме.

Если раскрыть оператор ГаМИJlI)тона, то получится уравнение

Шредингера в таком виде:

"n2

н= -- V'+ V"(x,y.z)

2т

,,2 2

-->'Ч'+V·Ч'=Е·Ч'

2т

n' 2 Ч'-(Е-V)Ч' =0

-->'

2т

V	2	2т
		Ч'+п-'(Е-V)Ч'=О

17

http://mitht.ru/e-library

В разных книгах по квантовой механике формулируется разное колlfчество

П()сryлатов. Три, отмеченные выше, обязательны. Еще в качестве

ПС>стулата формулируют и следующее С80ЙСТВО микросистемы:

Постулат 4

в квантовой механике собственное значение какого-либо оператора получается в том случае, если функция 'f')описывающая состояние системы, является собственной функцией данного оператора. Во всех

других случаях приходится иметь дело со средними значениями (или

ожидаемыми) мехаНических величин:

-fЧ"F'Pd,

,1=--;;--:-- fЧ"Ч'd,

Если функция нормирована, то

А == f'l"F'I'dr

Бели функция ЧJ известна, то среднее значение механической

величины можно определить, используя оператор F

данной

механJfЧеской велИЧИНЫ. Если же функция 'i' является собственной

функц..еЙ оператора F, то

,1= fЧ"F'Pd, = JЧ",1Ч'd,=,1 J'V'V'd,=,1

т.е. получается собственное значение оператора F.

Например, можно определить среднее значение (или ожидаемое) импульса частицы или одной из его компонент:

f'P( -;n ~)'P'dr

Р, -

f'P'P'dt

Такая ситуация может возникнуть 'в ТОМ случае, если СИС1'ема из n чаСiИЦ

характеризуется волновой функцией 'р. А мы для каждой из чаСТИЦ будем

определять ИЛИ координату х, или кинетическую энергию Т, или

компонент импульса Рх• или импульс р . Вот тогда мы сможем найти

ожидаемое ИЛИ среднее значение всех этих величин.

18

http://mitht.ru/e-library

1.3. Некоторые простые задачи квантовой механнки и

уравнение Шредингера

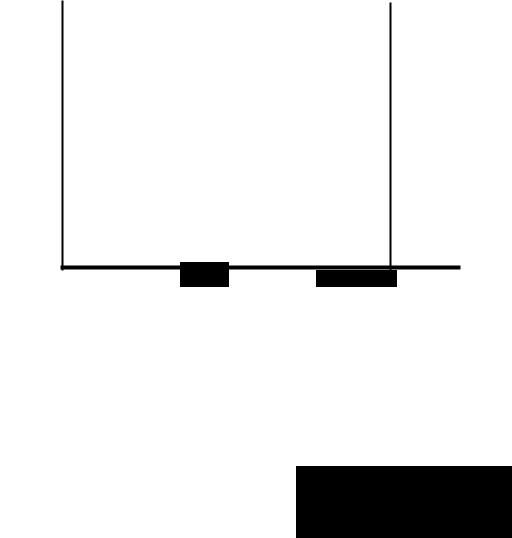
1.3.1. Электрон в nотеllциалыюм ящике

в квантовой механике рассмотрение различных физических систем

СВОДИТСЯ к решению уравнения l11редингера. При этом СНачала нужно

составить оператор Гамильтона, подставить его в уравнение и решить его.

Рассмотрим Сначала некоторые простые системы, которые имеют большое

значение ДJIЯ изучения молекулярных и кристаллических систем и для

спектроскопии, а также решим задачу, связанную с движением электрона в

ограниченном замкнутом пространстве. Представим себе мысленно

(физики любят ставить такие «мысленные» опыты), что мы поместили

электрон в ящик с бесконечно ВЫСОКИМИ стенками, внутри которого

потенциальная энергия равно нулю. Вне ящика она настолько велиКа, что электрон не может ВЫЙТИ из ящика. Допустим он двигается только вдоль

оси Х.

V:.O

х

РИС.I.3 а. )

Его состояние описывается. волновой фУliкцией "1:'. Тогда уравнение

Шредингера для него запишется так:

а''1' + 2т (Е_ 0)'1' = О

ах' 1;'

Если это уравнение решить, то получим, что "fI может иметь слсдуюший

вид:

Ч' =A·sinkx.. 'f!=B·coskx', '1'=A·sinkx+B·coskx

Какое выбрать? Для ЭТОГО нужно определить какое ИЗ ЭТИХ решений

удовлетворяет граничным условиям: ЧJ =0, когда Х = о и Х = L (т.е.

19

http://mitht.ru/e-library

электрон не может покинуть ящик). Таким требованиям удовлетворяет

'P=A-sinh (так как \f';.B-соskr удовлетворяет этим требованиям только

при В"" О, и тогда \f' всегда будет равна О. зто не roдиrся).

При X~L

подставить

	"q..t=o, если	""	",л· Ш'
			т = ·sш- х. Если
		kL=mr; k,,::--·- тогда
		L	L

\f' в уравнение Шредингера, то получим

d't' n1! А n1l

d 2\}J

-

n1g

1 А .

n;r

n l 7r

1

-с-=-

cos-x·

L'

sш-х=-

L'

Ч'

dx

L

L' dx'

L

n 27r 2

2т

E'I' = О

- --- Ч' + -

L'

,,'

n

2tt

2

81l

2m

E'I'

--Ч' =

h'

L'

'h'

Е=_n--,

8mL'

Это значит,

что

энерrnя

электрона

1'1 ящике

квантуется -

принимает

значения пропорциональные квадраry целых чисел n=1,2,З,... Если

пространство буде велико ( L велико), то

Еп+1 -Еп ~O

	Е	-Е =~'_r.(n+l)2_n2]			~O
	11+1	n	8mL2	~
			En.. 1 -
Если масса частицы велика, то				p~ 4 О И квантования энергии тоже не
будет.

Как себе это МОЖНО представить (рис.l.3 б)?

в силу двоiiственной природы, движение электрона носит волновой

характер_ В ограниченном пространстве волна может распространяться

только в том случае, если вдоль ДЛИНЫ укладывается целое число

полуволн, Т.е.

А.

L = n--

2

где n - любое целое положительное число (рис. 1.36)

При движении в трехмерном ящике (с длинами сторон а, Ь, С) электрон

имеет три степени свободы и его энергию можно рассматривать как сумму

составляющих по трем координатным осям, Т.е.

Е = Ех + Еу + Е,.

20

http://mitht.ru/e-library

Волновую функцию, описывающую состояние электрона. можно

представить как произведение трех функций, каждая ИЗ которых зависит только от ОДной координаты (ИСХОДЯ из вероятностных предстаВJlСНИЙ в описании СОСТОЯНИЯ микрочастиu. Вероятность сложного события равна

произведению вероятностей отдельных событий).

У:=оО !

I

РИС.l.3 б.

'у = Х(х). У(у). Z(z)

Тогда при решении уравнение Шредингера преобразуется в три обыкновенных дифференциальных уравнения, которые могут быть легко

решены.

В соответствии с граничными условиями

X~O и х=а, y~O и у=Ь, z=O и z=c

энергия электрона в трехмерном ящике будет определяться:

n 2 h'		n' h'	n' h'
Е =	х	+ У	+-:-'-'_;-
8та' 8тЬ'			8тс"
где nr , n1') nz - квантовые числа.
Таким образом, решение	уравнения Шредингера ДЛЯ электрона II

потенциальном яuщке привело к очень важному результату:

энергия электрона В ограниченном пространстве может ПРl-шимать лишь

определенные дискретные значения, т.е. квантуется. Это справедливо, не

только Д,1Я электрона, tЮ и для любой микрочастицы.

2\

http://mitht.ru/e-library