Семенов. Планирование эксперимента1

40

Возьмем для этого матрицу полного двухфактор-

ного эксперимента (табл. 9) и приравняем произведе-

ние X1X2 к фактору X3.

						Таблица 9
	Планирование типа 23-1
Номер	X1	X2	X1X2	X3		Функция
опыта						отклика
1	-1	-1	+1	+1		y1
2	+1	-1	-1	-1		y2
3	-1	+1	-1	-1		y3
4	+1	+1	+1	+1		y4

По формуле (2.8), вычислим:

1

b0=4(y1+y2+y3+y4)

По формуле (2.9) найдем:

1

b1=4(-y1+y2-y3+y4)

1

b2=4(-y1-y2+y3+y4)

41

В табл. 8 столбцы для произведения X1X2 и факто-

ра X3 полностью совпадают. Поэтому коэффициенты b12 и b3 не могут быть определены раздельно. С по-

мощью формулы (2.9) может быть найдена только их

сумма:

1

b12+b3=4(y1-y2-y3+y4)

Этот недостаток рассматриваемого плана является платой за уменьшение общего количества опытов с 8

до 4.

Планирование эксперимента, когда некоторые из факторов приравнивают к произведениям нескольких факторов, называют планированием со смешивани-

ем. Его обозначают символом 2n-p, где n - общее чис-

ло факторов, а р - число факторов, приравненных к произведениям. С этой точки зрения в табл. 8 приве-

дена матрица планирования типа 23-1.

www.mitht.ru/e-library

42

2.4. Устранение влияния временного дрей-

фа

Планирование со смешиванием иногда применяют

в тех случаях, когда необходимо устранить влияние

неуправляемых изменений во времени некоторых

влияющих факторов, называемое временным дрей-

фом.

При постановке большой серии опытов, требую-

щих длительного времени, всегда приходится опа-

саться нежелательных изменений исходных свойств

реагентов, катализаторов, некоторых характеристик оборудования и т.п. Влияние этого временного дрей-

фа на параметры математического описания процес-

са можно практически устранить, разбивая серию опытов на отдельные блоки так, чтобы эффект от временного дрейфа оказался смешанным с произве-

дениями факторов, для которых коэффициенты рег-

рессии достаточны малы.

Допустим, необходимо устранить влияние времен-

ного дрейфа на параметры уравнения регрессии, по-

лучаемого в результате полного трехфакторного экс-

перимента. С этой целью разобьем эксперимент на

43

два блока и введем новую независимую переменную

XД, характеризующую дрейф. Положим XД=X1X2X3.

В один из блоков отберем опыты, для которых

XД=+1, а в другой - для которых XД=-1. Формально это

планирование, приведенное в табл.9, можно рас-

сматривать как эксперимент типа 24-1 с генерирующим соотношением XД=X1X2X3.

Исходя из матрицы планирования, будем считать,

что в первом блоке все результаты опытов вследст-

вие временного дрейфа завышены на Д, а во втором

- занижены на ту же величину. Опыты первого блока,

рандомизировав, проведем в конце, а опыты второго

- в начале работы (или, наоборот, первый блок в на-

чале, второй в конце).

Если уравнение регрессии ищется в виде

y=b0+b1X1+b2X2+b3X3+b12X1X2+b23X2X3+

+b123X1X2X3

то коэффициенты регрессии будут являться следую-

щими оценками:

b0 0; b2 2

b1 1; b3 3

www.mitht.ru/e-library

44

b12 12; b23 23

b13 13; b123 123+ Д

Таблица 10

Планирование в условиях временного дрейфа

Номер	X1	X2	X3	XД=X1X2X3	Функция
блока					отклика
1	-1	-1	+1	+1	y1+ Д
	+1	-1	-1	+1	y2+ Д
	-1	+1	-1	+1	y3+ Д
	+1	+1	+1	+1	y4+ Д
2	-1	-1	-1	-1	y5- Д
	+1	-1	+1	-1	y6- Д
	-1	+1	+1	-1	y7- Д
	+1	+1	-1	-1	y8- Д

Рассчитаем, например, коэффициенты b1 и b123:

45

1

b1=8[-(y1+ д)+(y2+ д)-(y3+ д)+(y4+ д)-(y5- д)+

1

+(y6- д) --(y7- д)+(y8- д)]=8(-y1+y2-y3+y4-y5+y6-

-y7+y8)

1

b123=8[(y1+ д)+(y2+ д)+(y3+ д)+(y4+ д)-(y5- д)-(y6-

1

- д)-(y7- д)-(y8- д)]=8(y1+y2+y3+y4-y5-y6-y7-y8)+ д

Следовательно, все коэффициенты регрессии,

кроме b123, не содержат погрешностей, обусловлен-

ных временным дрейфом.

2.5. Интерпретация полученной модели

Адекватная линейная модель, которая рассматри-

вается в настоящей главе, имеет вид полинома пер-

вой степени. Коэффициенты полинома являются ча-

стными производными функции отклика по соответст-

вующим переменным. Их геометрический смысл –

www.mitht.ru/e-library

46

тангенсы углов наклона гиперплоскости к соответст-

вующей оси. Больший по абсолютной величине ко-

эффициент соответствует большему углу наклона и,

следовательно, более существенному изменению па-

раметра оптимизации при изменении данного факто-

ра.

Перевод модели на язык экспериментатора назы-

вается интерпретацией модели [7]. Задача интер-

претации весьма сложна. Ее решают в несколько этапов. Первый этап состоит в следующем. Устанав-

ливается, в какой мере каждый из факторов влияет на параметр оптимизации. Величина коэффициента

регрессии - количественная мера этого влияния. Чем больше коэффициент, тем сильнее влияет фактор. О

характере влияния факторов говорят знаки коэффи-

циентов. Знак плюс свидетельствует о том, что с уве-

личением значения фактора растет величина пара-

метра оптимизации, а при знаке минус - убывает. Ин-

терпретация знаков при оптимизации зависит от того,

ищем ли мы максимум или минимум функции отклика.

Если y max, то увеличение значений всех факторов,

коэффициенты которых имеют знак плюс, благопри-

47

ятно, а имеющих знак минус - неблагоприятно. Если

же y min, то, наоборот, благоприятно увеличение

значений тех факторов, знаки коэффициентов кото-

рых отрицательны.

Далее выясняется, как расположить совокупность факторов в ряд по силе их влияния на параметр оп-

тимизации. Факторы, коэффициенты которых незна-

чимы, не интерпретируются. Можно только сказать,

что при данных интервалах варьирования и ошибке воспроизводимости они не оказывают существенного влияния на параметр оптимизации.

Изменение интервалов варьирования приводит к

изменению коэффициентов регрессии. Абсолютные величины коэффициентов регрессии увеличиваются с увеличением интервалов. Инвари-

антными к изменению интервалов остаются знаки

линейных коэффициентов регрессии. Однако и они изменятся на обратные, если при движении по гради-

енту (гл. 3) мы "проскочим" экстремум.

Теперь мы получили основу для перехода к сле-

дующему этапу. Априорные сведения дают некото-

рые представления о характере действия факторов.

www.mitht.ru/e-library

48

Источниками таких сведений могут служить теория

изучаемого процесса, опыт работы с аналогичными

процессами, предварительные процессы и т.д.

Если, например, ожидается, что с ростом темпера-

туры должно происходить увеличение параметра оп-

тимизации, а коэффициент регрессии имеет знак ми-

нус, то возникает противоречие. Возможны две при-

чины возникновения такой ситуации: либо в экспери-

менте допущена ошибка, и он должен быть подверг-

нут ревизии, либо неверны априорные представле-

ния. Нужно иметь ввиду, что эксперимент проводится в локальной области факторного пространства и ко-

эффициент отражает влияние фактора только в этой области. Заранее не известно, в какой мере можно распространить результат на другие области. Теоре-

тические же представления имеют обычно более об-

щий характер. Кроме того, априорная информация часто основывается на однофакторных зависимостях.

При переходе к многофакторному пространству си-

туация может изменяться. Поэтому мы должны быть уверены, что эксперимент проведен корректно. Тогда

для преодоления противоречия можно выдвигать

49

различные гипотезы и проверять их эксперименталь-

но.

В тех, довольно редких, случаях, когда имеется

большая априорная информация, позволяющая вы-

двигать гипотезы о механизме явлений, можно перей-

ти к следующему этапу интерпретации. Он сводится к проверке гипотез о механизме явлений и выдвиже-

нию новых гипотез.

Получение информации о механизме явлений не является обязательным в задачах оптимизации, но возможность такого рода следует использовать.

Здесь особое внимание приходится уделять эффек-

там взаимодействия факторов.

Пусть в некоторой задаче взаимодействие двух факторов значимо и имеет положительный знак. Это свидетельствует о том, что одновременное увеличе-

ние, как и одновременное уменьшение, значений двух факторов приводит к увеличению параметра оптими-

зации (без учета линейных эффектов). Если эффект взаимодействия факторов x1 x2 имеет отрицательный знак, то любая комбинация разных знаков x1 и x2 при-

водит к росту параметра оптимизации.

www.mitht.ru/e-library

50

Интерпретация эффектов взаимодействия не так

однозначна, как линейных эффектов. В каждом слу-

чае имеется два варианта. Какому из вариантов от-

давать предпочтение? Прежде всего, нужно учесть

знаки линейных эффектов соответствующих факто-

ров. Если эффект взаимодействия имеет знак плюс и соответствующие линейные эффекты отрицательны,

то выбор однозначен: сочетание -1 и -1. Однако воз-

можен случай, когда знаки линейных эффектов раз-

личны. Тогда приходится учитывать численные зна-

чения коэффициентов и жертвовать самым малым эффектом.

Иногда приходится учитывать технологические со-

ображения: например, эксперимент в одной области факторного пространства дороже (или труднее), чем

вдругой.

Взаключение этого параграфа следует остано-

виться на интерпретации эффектов взаимодействия высоких порядков. Если значимым оказался эффект взаимодействия трех факторов, например x1x2x3, то его можно интерпретировать следующим образом.

Этот эффект может иметь знак плюс, если отрица

51

тельные знаки будут у четного числа факторов (ноль или любые два). Знак минус будет, если нечетное число факторов имеет знак минус (все три или любой один). Это правило распространяется на взаимодей-

ствия любых порядков. Используют еще такой прием:

произведение двух факторов условно считают одним

фактором и сводят трехфакторное взаимодействиее к

парному и т.д.

3.Оптимизация

3.1.Метод крутого восхождения

Впредыдущей главе были рассмотрены методы

построения экспериментально-статистических моде-

лей в виде уравнений регрессии. Теперь рассмотрим вопрос, как использовать эти модели для оптимиза-

ции процессов или свойств многокомпонентных сис-

тем.

Следует иметь ввиду, что качество процесса

обычно характеризуется несколькими функциями от-

клика. Однако обычно невозможно найти такое соче-

тание значений влияющих факторов, при котором од

www.mitht.ru/e-library

52

новременно достигаются экстремумы всех интере-

сующих экспериментатора функций отклика. Напри-

мер, максимальная производительность оборудова-

ния и минимальная себестоимость продукции обычно

достигаются при различных технологических режи-

мах.

Как влияющие факторы, так и функции отклика мо-

гут изменяться только в определенных пределах. На-

пример, концентрации реагентов не могут быть отри-

цательными, температура и давление в аппарате не могут превышать безо-пасных пределов, себестои-

мость продукции должна быть не выше плановой.

Следовательно, оптимизацию процессов, как прави-

ло, осуществляют в условиях ограничений на влияющие факторы и функции отклика.

Величина, характеризующая уровень оптимизации процесса, называется критерием оптимальности. В

планировании эксперимента обычно критерием опти-

мальности является одна из функций отклика, харак-

теризующих процесс.

Оптимизация процесса представляет собой целе-

направленный поиск значений влияющих факторов,

53

при которых достигается экстремум критерия опти-

мальности (с учетом ограничений, наложенных на все

влияющие факторы и функции отклика).

Д.Бокс и К.Уилсон предложили использовать для

оптимизации результаты полного факторного экспе-

римента или эксперимента по методу дробных реп-

лик. Сущность такой оптимизации состоит в следую-

щем.

Пусть, например, критерием оптимальности слу-

жит функция отклика y, представленная в виде урав-

нения регрессии (2.3). Один из влияющих факторов принимают за базовый и для него вычисляют произ-

ведение соответствующего коэффициента регрессии на шаг варьирования. В качестве шага варьирования обычно берут интервал варьирования из условий полного факторного эксперимента. Например,

для первого фактора это произведение имеет вид b1 x1.

Затем для базового фактора выбирают шаг дви-

жения, с которым будет осуществляться оптимиза-

ция. Обычно x1* x1. После этого вычисляют отно-

шение

www.mitht.ru/e-library

		54
	x*	(3.1)
	1

b1 x1

Для всех остальных факторов шаги движения к оп-

тимальным значениям рассчитывают по формуле:

xi*= bi xi (3.2)

Движение к оптимуму начинают из центра плана,

который использовался для получения математиче-

ского описания функции отклика. Значения факторов

на каждом новом шаге находят путем прибавления

xi* к соответствующим предыдущим значениям. Так

осуществляется оптимизация по методу крутого вос-

хождения.

Если же ищется минимум функции y, то новые значения факторов находят из предыдущих путем

вычитания xi*. Такой способ оптимизации называют

методом наискорейшего спуска.

Движение к оптимуму прекращают в следующих случаях:

1. Значения одного или нескольких факторов или функций отклика вышли на границы допустимых зна-

чений.

55

2. Достигнут экстремум критерия оптимальности y.

В первом случае на этом оптимизация заканчива-

ется, во втором - в области экстремума функции y

ищут ее новое математическое описание, используя

полный факторный эксперимент или метод дробных

реплик. Если удается получить адекватное описание этой функции в виде (2.3), то продолжают оптимиза-

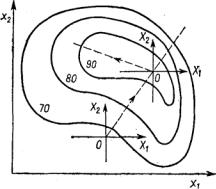
цию методом крутого восхождения (рис.5). В этом случае оптимум, найденный в результате первого крутого восхождения, был локальным.

Если в области оптимума не удается получить адек-

ватного уравнения регрессии вида (2.3), то переходят

к планированию эксперимента для получения мате-

матического описания функции y в виде многочлена

второй степени. Методика проведения таких экспе-

риментов будет рассмотрена в следующей главе.

www.mitht.ru/e-library

56
	Пример 3.1. Пусть в ре-
	зультате	полного фак-
	торного	эксперимента
	(пример	2.1)	получено
	адекватное		уравнение
	регрессии
	y1=35.6+1.95X1-
Рис. 5. Оптимизация по ме-		1.35X2
тоду крутого восхождения.	Здесь, как и в примере

2.1, y1 - выход продукта реакции, X1 - температура, X2

- концентрация реагента.

Введем также в рассмотрение функцию отклика y2,

характеризующую скорость химической реакции

(кмоль.м-3.ч-1). Пусть требуется, чтобы выполнялось условие y2 2.5.

Допустим, что ограничения на влияющие факторы имеют вид

30 x1 120

10% x2 70%

Будем оптимизировать выход продукта реакции методом крутого восхождения.

57

В качестве базового фактора возьмем температу-

ру и примем шаг движения на крутом восхождении 4 ,

тогда

	x*		4	041.
	1
	b1 x1
			195. 5

Здесь x1 взят по условиям полного факторного экс-

перимента (пример 2.1).

Шаг по концентрации на крутом восхождении ра-

вен

x2*= b2 x2=0.41(-1.35).1=-0.55о

Для удобства ведения эксперимента шаги движе-

ния, рассчитанные по формуле (3.2), можно несколь-

ко округлять. В данном случае удобно принять x2*=-

0.5o.

Результаты опытов, выполненных по методу кру-

того восхождения, приведены в табл. 11,

Здесь y1p и y1э - соответственно расчетные и экспе-

риментальные значения выхода продукта реакции,

yэ2 - экспериментально найденные скорости реакции.

Шаги движения и координаты опытов крутого вос

www.mitht.ru/e-library

58

Таблица 11.

Результаты опытов по методу крутого восхождения

Характерист.	x1		x2	X1	X2		yp	yэ	yэ
и № опыта							1	1	2
Центр плана	50		25	0	0		35.6	35.1	2.9
Интервал
варьирования	5		1	1	1		-	-	-
Шаг движе-	4		-0.5	0.8	-0.5		-	-	-
ния
		Крутое восхождение
Опыт N 1	54	24.5		0.8	-0.5		36.5	36.9	3.2
Опыт N 2	58	24.0		1.6	-1.0		37.4	37.2	3.7
Опыт N 3	62	23.5		2.4	-1.5		38.2	38.5	2.8
Опыт N 4	66	23.0		3.2	-2.0		39.1	40.7	2.3
Опыт N 5	70	22.5		4.0	-2.5		40.0	38.1	1.9
Опыт N 6	74	22.0		4.8	-3.0		40.9	37.2	1.6

хождения в кодированных переменных рассчитыва-

ются по формуле (2.1) с использованием физических

59

переменных x1, x2 и шагов варьирования, принятых

ранее в полном факторном эксперименте.

Как видно из табл.11, в опыте N 4 достигнут мак-

симальный выход продукта реакции, однако скорость

процесса в этом случае меньше допустимого значе-

ния. Оптимальным режимом процесса следует считать условия опыта N 3. Ограничения на x1 и x2 в ходе оптимизации не нарушены.

3.2. Симплексный метод

Симплексом называется правильный многогранник, имеющий n+1 вершину, где n - число факторов,

влияющих на процесс. Если факторов два, то сим-

плексом является правильный треугольник. Сущность симплексного метода оптимизации иллюстрируется рис.6.

www.mitht.ru/e-library