Семенов. Планирование эксперимента1

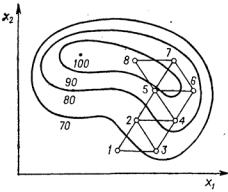
60

Начальная серия

опытов соответству-

ет вершинам исход-

ного симплекса (точ-

ки 1, 2, и 3). Условия этих первых опытов берутся из области

Рис. 6. Оптимизация по симзначений факторов,

плексному методу.

соответствующих наиболее благопри-

ятным из известных режимов оптимизируемого про-

цесса.

Сравнивая между собой результаты опытов в точ-

ках 1, 2 и 3, находят среди них самый плохой с точки зрения выбранного критерия оптимальности. Пусть,

например, самым "неудачным" оказался опыт в точке

1. Этот опыт исключают из рассмотрения, а вместо него в состав симплекса вводят опыт в точке 4, кото-

рая симметрична точке 1 относительно противопо-

ложной стороны треугольника, соединяющей точки 2

и 3.

61

Далее сравнивают между собой результаты опы-

тов в вершинах нового симплекса, отбрасывают са-

мый неудачный из них и переносят соответствующую

вершину симплекса в точку 5. Затем эта процедура

повторяется в течение всего процесса оптимизации.

Если достигнут экстремум критерия оптимальности,

то дальнейшее движение симплекса прекращается.

Это значит, что новый шаг возвращает исследовате-

ля в предыдущую точку факторного пространства,

либо симплекс начинает "вращаться" вокруг точки оп-

тимума.

Симплексный метод, также как и метод крутого

восхождения, является локальным методом поиска экстремума. Если существует несколько экстремумов критерия оптимальности, то этот метод позволяет найти тот из них, кото-

рый расположен ближе к точкам исходного симплек-

са. Поэтому, если есть подозрение о существовании нескольких экстремумов критерия оптимальности, то нужно осуществить их поиск, каждый раз начиная оп-

тимизацию из новой области факторного пространст-

ва. Затем следует сравнить между собой найденные

www.mitht.ru/e-library

62

оптимальные условия и из всех вариантов выбрать

наилучший.

При оптимизации необходимо принимать во вни-

мание ограничения, наложенные на влияющие фак-

торы и функции отклика.

При использовании симплексного метода не обя-

зательно дублировать опыты, т.к. ошибка в отдельном опыте может только несколько замедлить оптимизацию. Если же последующие опыты выполняются безупречно, то движение к оптимуму продолжается.

Матрица опытов исходного симплекса в кодиро-

ванных переменных приведена в табл.12. Символом

"0" обозначены координаты центра плана, т.е. основ-

ной уровень.

Величины, входящие в эту таблицу, рассчитыва-

ются по следующим формулам:

ki	1	(3.3)
	2i(i 1)
	Ri=iki	(3.4)

где i - номер фактора в матрице планирования.

63

Таблица 12

Матрица исходного симплекса

№	X1	X2	...	Xn-1	Xn	Функция
опыта						отклика
1	k1	k2	...	kn-1	kn	y1
2	-R1	k2	...	kn-1	kn	y2
3	0	-R2	...	kn-1	kn	y3
...	...	...	...	...	...	...
n-1	0	0	...	kn-1	kn	yn-1
n	0	0	...	-Rn-1	kn	yn
n+1	0	0	...	0	-Rn	yn+1

Опыты, представленные в табл. 11, соответствуют

вершинам симплекса, сторона которого равна едини-

це, а центр совпадает с началом координат (в коди-

рованных переменных).

Результаты расчетов, выполненных на основании табл. 12 и формул (3.3) и (3.4), приведены в табл. 13.

Аналогично можно рассчитать условия исходной

серии опытов для большего количества факторов. Наибольшее количество опытов приходит

www.mitht.ru/e-library

64

ся ставить в начале эксперимента. Затем на каждом

шаге оптимизации выполняется только один опыт.

Приступая к оптимизации, необходимо с помощью

табл. 12 или 13 рассчитать матрицу исходной серии

опытов в физических переменных, пользуясь форму-

лой

xi=x0i+ xiXi (3.5)

где использованы те же обозначения, что и в форму-

ле (2.1). В дальнейшем все операции производятся

только с физическими перемен-

ными.

				Таблица 13
Условия начальной серии опытов
Номер	X1	X2	X3		X4
опыта
1	0.5	0.289	0.204		0.158
2	-0.5	0.289	0.204		0.158
3	0	-0.578	0.204		0.158
4	0	0	-0.612		0.158
5	0	0	0		-0.632

65

Условия каждого нового опыта рассчитываются по

формуле

			2	n 1
x				( x		x*) x*		(3.6)
			n
	i			j 1	ji	i	i

где n - число факторов в матрице планирования; j - номер опыта;

i - номер фактора;

xi* - значение i-го фактора в самом неудачном

опыте предыдущего симплекса.

На любом шаге оптимизации, осуществляемой

симплексным методом, можно включить в программу

исследований новый фактор, который до тех пор не принимался во внимание, но оставался на постоян-

ном уровне. При этом значения всех ранее рассмат-

риваемых факторов рассчитываются по формуле

			1	n 1
x	i			x	ji	(3.7)
			n 1 j 1

где i=1,2,...,n, т.е. являются средними арифметиче-

скими значениями соответствующих координат пре-

дыдущего симплекса.

Значение вновь вводимого фактора определяется

www.mitht.ru/e-library

66

по формуле

xn+1=x0(n+1)+ xn+1(Rn+1+kn+1) (3.8)

где x0(n+1) - основной уровень этого фактора;

xn+1 - выбранный шаг варьирования для данного фактора;

Rn+1, kn+1 - величины, рассчитываемые по форму-

лам (3.3) и (3.4).

Добавление нового фактора в состав полного

факторного эксперимента сопровождается увеличе-

нием количества опытов вдвое. В этом смысле сим-

плексный метод имеет очевидное преимущество.

В практику научных исследований симплексный

метод был введен Ф.Химсвортом в 1962 г.

Пример 3.2 Пусть требуется с помощью симплексно-

го метода оптимизировать выход целевого продукта y (%), который получается при взаимодействии двух реагентов с концентрациями x1 и x2 (кмоль.м-3) при

температуре x3 (oС).

Выберем основные уровни и шаги варьирования факторов и сведем их в табл. 14.

Пользуясь формулой (3.5) и табл.12, рассчитаем ус-

ловия проведения первых четырех опытов и получен-

67

Таблица 14

Значения уровней факторов и шагов

варьирования

Фактор	Основной	Шаг
	уровень	варьирования
x1, кмоль.м-3	1.0	0.1
x2, кмоль.м-3	1.5	0.2
x3, oC	60.0	5.0

ные результаты сведем в табл.15.

Например, для третьего опыта

x31=1+0.1.0=1

x32=1.50+0.2(-0.578)=1.38 x33=60+5.0.204=61

Здесь первый индекс обозначает номер опыта, а

второй - номер фактора.

Сравнивая между собой результаты первых четырех опытов, видим, что самый низкий выход целевого продукта получился в третьем опыте. Этот опыт сле-

дует исключить из дальнейшего рассмотрения.

www.mitht.ru/e-library

68

Таблица 15

Условия и результаты планирования

по симплексному методу

Номер	x1	x2	x3	Функция
опыта				отклика
1	1.05	1.56	61	72.3
2	0.95	1.56	61	70.1
3	1.00	1.38	61	65.4
4	1.00	1.50	57	68.2
5	1.00	1.70	58	73.9
6	1.00	1.72	63	76.5

Заменим его опытом N 5, условия проведения которо-

го рассчитаем по формуле (3.6):

x51=(2/3)(1.05+0.95+1.00)-1.00=1.00 x52=(2/3)(2.1.56+1.50)-1.38=1.70 x53=(2/3)(2.61+57)-61=58

В новом симплексе, образованном опытами N 1, 2,

4 и 5, самым "неудачным" является опыт N 4. Его за-

меним опытом N 6, условия которого найдем, пользу-

ясь той же формулой (3.6).

69

Далее процедура оптимизации может быть про-

должена аналогично.

Рассмотрим теперь вопрос о том, как включить в

программу исследований еще один фактор, напри-

мер, скорость вращения мешалки. Пусть до этих пор

она была постоянной и равной 500 об/мин. Теперь будем считать эту величину фактором x4 и примем

для нее шаг варьирования x4=100 об/мин.

Предыдущий симплекс для трех факторов (см.

табл.15) состоит из опытов N 1,2,5 и 6. Чтобы из него получить новый симплекс для четырех факторов,

введем опыт N 7 (табл.16). Условия проведения опы-

та N 7 найдем по формулам (3.7) и (3.8):

x71=(1/4)(1.05+0.95+2.1.00)=1.00 x72=(1/4)(2.1.56+1.70+1.72)=1.64 x73=(1/4)(2.61+58+63)=61

x74=500+100(0.632+0.158)=579 580

Далее оптимизацию можно продолжить с учетом

всех четырех факторов, пользуясь рассмотренной выше процедурой.

www.mitht.ru/e-library

70

				Таблица 16.
Симплексный план эксперимента
	для четырех факторов
Номер	x1	x2	x3	x4	Функция
опыта					отклика
1	1.05	1.56	61	500	72.3
2	0.95	1.56	61	500	70.1
5	1.00	1.70	58	500	73.9
6	1.00	1.72	63	500	76.5
7	1.00	1.64	61	580	78.1

4. Исследование области оптимальных

условий. Ортогональное центральное

композиционное планирование

Процесс оптимизации приводит в область фактор-

ного пространства, где кривизна поверхности отклика велика и вследствие этого поверхность не может быть описана многочленом вида (2.3). Для адекватно-

го математического описания здесь требуется много-

член более высокой степени, например, второй. С

71

этой целью используют центральное композицион-

ное планирование эксперимента (ЦКП). Одним из ви-

дов

ЦКП является ортогональное ЦКП. Количество опы-

тов при ортогональном ЦКП определяется по форму-

ле

N=2n+2n+1 (4.1)

где 2n - количество опытов, образующих полный фак-

торный эксперимент;

2n - число точек в факторном пространстве,

имеющих координаты ( ,0,0,...,0); (0, ,0,...,0),...,

(0,0,..., ). Эти точки называются звездные, а вели-

чина - звездным плечом;

1 - опыт в центре планирования, т.е. в точке факторного пространства с координатами (0,0,...,0) (В

общем случае в центре планирования может быть несколько опытов). Если с помощью полного фактор-

ного эксперимента не удается получить адекватного математического описания в форме (2.3), то к нему добавляют опыты в "звездных" точках и в центре плана, а полученную при этом композицию использу-

ют для получения матема

www.mitht.ru/e-library

72

тического описания процесса в виде многочлена вто-

рой степени. Отсюда и произошло название метода -

центральное композиционное планирование.

Значения звездного плеча для ЦКП с различным

числом факторов n следующие:

n	.............2	3	4	5
..........	1.000	1.215	1.414	1.547

Эти значения выбраны из условия ортогональ-

ности матрицы планирования.

Уравнение регрессии при ортогональном ЦКП ищут в следующем виде:

y=bo*+b1X1+b2X2+...+bnXn+b12X1X2+...+b(n-1)nXn-

	1Xn+ +b11X1*+...+bnnXn*						(4.2)
	Переменные величины
				1	N
	X*	X2			X2		(4.3)
	ji	ji		N j 1		ji

где j - номер опыта; i - номер фактора, введены для

того, чтобы матрица планирования была ортогональ-

на, и коэффициенты регрессии определялись незави-

симо друг от друга по результатам опытов.

Для того чтобы получить уравнение регрессии в

73

обычной форме

y=bo+b1X1+b2X2+...+bnXn+b12X1X2+...

+b(n-1)nXn1Xn+ +b11X12+b22X22+...+bnnXn2											(4.4)
находят величину
				b11	N			bnn	N
b		b*			X2		...		X2		(4.5)
	0	0		N j 1		j1		N j 1		jn

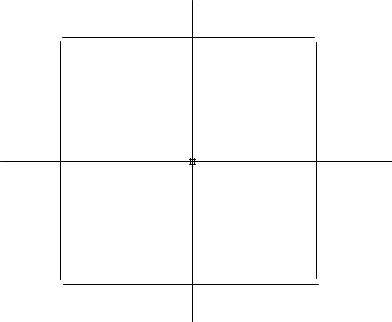
В табл.17 приведена в качестве примера матрица ортогонального ЦКП для двух факторов, а на рис.7

изображена схема этих опытов.

Коэффициенты регрессии при ортогональном ЦКП

рассчитываются по следующим формулам:

			1	N
	b*			y			(4.6)
0			N j 1			j
	N
	Xjiyj
bi	j 1				(где i 0)		(4.7)
	N
	(Xji )2

j 1

www.mitht.ru/e-library

74

X2

	*	+1
o		o

*	0	*
-1		+1	X1

o	*	o
		-1

Рис.7. Схема опытов ортогонального ЦКП для двух

факторов: - полный факторный эксперимент; * - опы-

ты в звездных точках;		- опыт в центре плана.
	N
	X*jiyj
bii	j 1	(4.9)
	N

(X*ji )2 i 1

Для расчета оценок дисперсий в определении ко-

эффициентов регрессии используют следующие вы-

75

ражения:

s2

s2*

y

(4.10a)

N

b0

ns2

N

s2

s2*

bii

X2

(4.10б)

b0

b0

N

j 1

ji

Таблица 17

Ортогональное ЦКП для двух факторов

Системы

Номер

X1

X2

X1X2

X1*

X2*

опытов

опыта

Полный

1

-1

-1

+1

+0.33

+0.33

факторный

2

+1

-1

-1

+0.33

+0.33

эксперимент

3

-1

+1

-1

+0.33

+0.33

4

+1

+1

+1

+0.33

+0.33

Опыты в

5

+1

0

0

+0.33

-0.67

звездных

6

-1

0

0

+0.33

-0.67

точках

7

0

+1

0

-0.67

+0.33

8

0

-1

0

-0.67

+0.33

Опыт в цен-

тре плана

9

0

0

0

-0.67

-0.67

www.mitht.ru/e-library

76

			s2
	s2		y			(где i 0)		(4.10в)
			N
	bi
			(Xji )2
			j 1
			s2
s2			y			(где i k)		(4.11)
		N
bik
		(XjiXjk )2
		j 1
						s2
			s2			y		(4.12)
						N
			bii
					(X*ji )2
					j 1
Коэффициент				bi	cчитается значимым,			если

bi >sbi t. Аналогично проверяется значимость ос-

тальных коэффициентов регрессии. Проверка адек-

ватности уравнения регрессии осуществляется с по-

мощью критерия Фишера.

Вычислить коэффициенты регрессии можно при помощи ППП Mathcad 8 PRO [5]. Для этого вводится матрица значений факторов X и вектор значений

функции отклика в виде Y. Далее используется функ-

ция b=regress(X,Y,n), где n – степень полинома, в

данном случае n=2. В результате мы получаем вектор

77

коэффициентов b. Следует иметь ввиду, что распо-

ложение коэффициентов в столбце вектора следую-

щее (снизу вверх): b11, b1, b0, b2, b22, b12.

Вычисление коэффициентов регрессии с исполь-

зованием современных ППП облегчает использова-

ние планов с другими критериями оптимальности, в

частности D-оптимальных планов. D-оптимальные планы характеризуются максимальной точностью предсказания. Среди композиционных планов второго порядка D-оптимальными являются планы со звезд-

ным плечом, равным единице. Можно также исполь-

зовать планы со звездным плечом, близким к едини-

це. В работе [8] показано, что наиболее точное пред-

сказание имеет место при длине звездного плеча в пределах 0.8-1.2.

После получения уравнения регрессии необходи-

мо исследовать форму поверхности отклика для пра-

вильного выбора оптимального режима технологиче-

ского процесса.

Построить поверхность отклика можно при помо-

щи ППП «Mathcad 8 PRO» [5,6]. Для этого предвари-

тельно вычисляют значение функции на прямоуголь

www.mitht.ru/e-library

78

ной сетке, то есть строят таблицу значений функции.

С этой целью вводят с клавиатуры имя функции двух

переменных f(x,y), знак равенства и выражение для

ее вычисления. Далее присваивают переменной N

значение, равное количеству узлов квадратной сетки

в плоскости переменных x, y. Определяют диапазон изменения целых индексов i и j узлов сетки xi, yj соот-

ветственно. Для этого вводят i:=0..N и j:=0..N. Далее определяют значения xi и yj в некотором диапазоне с определенным шагом посредством выражения, в со-

став которого входят индексы i и j. Табличные значе-

ния zij определяют как значение функции в узлах сет-

ки, zij=f(xi,yj). Далее в позиции Insert главного меню из открываемого при помощи команды Graph перечня типов трехмерной графики выбирают Surface Plot –

создать шаблон для построения трехмерного графи-

ка, вводят в помеченной позиции имя z и щелкают по рабочему документу вне поля графиков.

79

5. Планирование эксперимента при

изучении диаграмм состав-свойство

5.1. Метод симплексных решеток

При изучении свойств смеси, зависящих только от соотношений компонентов, факторное пространство представляет собой правильный (q-1)-мерный сим-

плекс [9]. Для систем выполняется соотношение

q
xi	1,	(5.1)
i 1

где xi 0 - концентрация компонента; q - количество

компонентов.

Для двухкомпонентных систем симплекс - прямая:

содержание компонентов определяется соотношени-

ем отрезков. При q=3 правильный симплекс - равно-

сторонний треугольник. Каждая точка треугольника отвечает одному определенному составу тройной системы и, наоборот, каждый состав представляется одной определенной точкой. Состав может быть вы-

ражен в мольных, весовых или объемных долях или процентах. Вершины треугольника соответствуют чистым веществам, стороны - двойным системам.

www.mitht.ru/e-library