Таблица производных

Таблица неопределенных интегралов

Методы интегрирования оду

Метод Эйлера

Усовершенствованный метод Эйлера

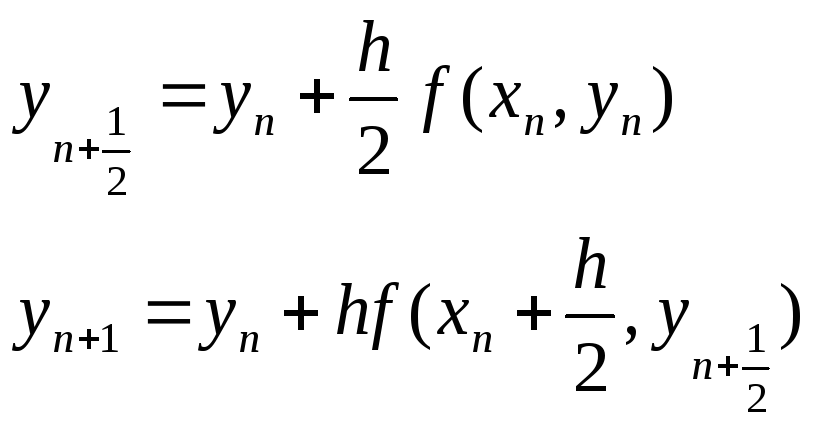
Метод предиктор – корректор

Метод Рунге-Кутта

Правило Рунге оценки погрешности. Экстраполяция Ричардсона.

Приведенная формула (4.25) для оценки погрешности квадратурных формул использует значения производных подинтегральной функции, что требует дополнительного анализа и вычислений. В связи с этим получило распространение практическоеправило Рунге оценки погрешности.

Идея состоит в том, чтобы организовав вычисления значений интеграла по нескольким семействам (множествам) узлов, затем сравнить результаты вычислений и получить оценку погрешности. Наиболее удобное правило связано с вычислением интеграла дважды: L_N[f],L_2N[f].

Правило Рунге оценки погрешности R_2N[f]:

R2N[f] ≈ (L2N[f] - LN[f] ) / ( 2^p -1 )

(4.32)

где p- порядок погрешности квадратурной формулы.

Определение 4.7Оценка погрешности, которая находится до решения задачи, называетсяаприорной.

Такую оценку дает теорема о погрешности.

Определение 4.8Оценка погрешности, которая находится после решения задачи, называетсяапостериорной.

Эту оценку дает правило Рунге.

После подсчета величин L_N[f] иL_2N[f] кроме оценки погрешности по правилу Рунге можно также дополнительно уточнить приближенное значение интеграла. Величина

L^*2N[f] = (2^pL2N[f] - LN[f] ) / ( 2^p -1 )

(4.33)

называется уточненным (или экстраполированным) по Ричардсонузначением искомого интеграла.

Погрешность L_N[f] -L^*_2N[f] имеет более высокий порядок относительноh, чемL[f]-L_N[f] (и, соответственно,L[f]-L_2N[f]). Именно, еслиL[f]-L_N[f]=ch^p+O(h^p+l), гдеl > 0 и константаc≠ 0 не зависит отh, тоL_N[f] -L^*_2N[f]=O(h^p+l). Более подробно эти вопросы разобраны в работе[6].

Для практического вычисления интеграла L[f] с заданной точностью ε выбирается некоторое начальное числоNразбиений отрезка [a,b] и вычисляются величиныL_N[f] иL_2N[f]. Если |R_2N[f]| ≤ ε, то с точностью ε полагаютL[f]≈L_2N[f] (либо более точноL[f]≈L^*_2N[f]). В противном случае вычисляют значениеL_4N[f] и сравнивают |R_4N[f]| и ε, и т.д.

R_2N[f] ≈ (L_2N[f] - L_N[f] ) / ( 2^p -1 )

А. Варианты заданий (решить методами Эйлера и Рунге-Кутта и сравнить точность с использованием правила Рунге

;

;

;

;

;

;

;

;

;

;

;

;

;

;

;

;

Б. Варианты заданий

6) y''- y = e^x, y(0) = 0, y'(0) = 0.5 на [0,1]. 7) y''-2 y' = x² -1, y(1) = -1/6, y'(1) = -3/4 на [1,2]. 8) y''- 2y' = 3e^x, y(0.3) = 1.415, y'(0.3) = 5.83 на [0.3, 0.6]. 9) y''+ y' = 3x², y(1) = -1, y'(1) = 2 на [1,2].

;

;

Ораторная работа 8

ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ. КРАЕВАЯ ЗАДАЧА

http://crecs.ru/ru/numlabs2/ODEBVP.html

1. Введение

Эта работа знакомит с различными методами решения линейных и нелинейных краевых задач. Отличие краевой задачи от задачи Коши (задачи с начальными условиями) состоит в том, что решение дифференциального уравнения должно удовлетворять граничным условиям, связывающим значения искомой функции более чем в одной точке.

Простейшим представителем краевой задачи является двухточечная граничная задача, для которой граничные условия задаются в двух точках, как правило, на концах интервала, на котором ищется решение. Двухточечные граничные задачи встречаются во всех областях науки и техники. На примерах таких задач и будет рассмотрено применение методов, обсуждаемых в настоящей работе. В случае задания краевых условий в более общем виде использование этих методов не представит принципиальных затруднений.