
- •Методы интегрирования оду
- •Ораторная работа 8
- •1. Введение
- •2. Теоретическая справка
- •2.1. Пример краевой задачи
- •2.2. Линейная краевая задача
- •2.3. Метод численного построения общего решения
- •2.4. Конечно-разностный метод (метод прогонки)
- •2.5. Нелинейная краевая задача
- •2.6. Метод стрельбы
- •2.7. Вычислительная неустойчивость задачи Коши
- •2.8. Метод линеаризации (метод Ньютона)
- •2.9. Библиографическая справка
- •3. Задание
- •4. Контрольные вопросы
2.6. Метод стрельбы
М етод
стрельбы для решения краевой задачи
(8.3) базируется на том, что имеются удобные
способы численного решения задачи Коши,
т. е.
задачи следующего вида
етод
стрельбы для решения краевой задачи
(8.3) базируется на том, что имеются удобные
способы численного решения задачи Коши,
т. е.
задачи следующего вида
![]()
![]()
![]() (8.4)
(8.4)
![]()
где
![]() —
ордината точки
—
ордината точки
![]() из
которой выходит интегральная кривая;— угол наклона
интегральной кривой к осиxпри
выходе из точки
из
которой выходит интегральная кривая;— угол наклона
интегральной кривой к осиxпри
выходе из точки
![]() (рис. 8).
При фиксированном
(рис. 8).
При фиксированном
![]() решение
задачи (8.4) имеет вид
решение
задачи (8.4) имеет вид
![]() При
При
![]() решение
решение
![]() зависит
только от:
зависит
только от:
![]()
Используя указанное замечание о решении
задачи Коши (8.4), можно задачу (8.3)
переформулировать следующим образом:
найти такой угол
![]() при
котором интегральная кривая, выходящая
из точки
при
котором интегральная кривая, выходящая
из точки
![]() под
угломк оси абсцисс,
попадет в точку
под
угломк оси абсцисс,
попадет в точку
![]()
![]() (8.5)
(8.5)
Р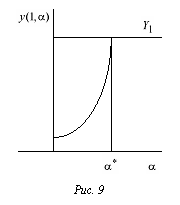 ешение
задачи (8.4) при этом
ешение
задачи (8.4) при этом
![]() совпадает
с искомым решением задачи (8.3). Таким
образом, дело сводится к решению уравнения
(8.5) (рис. 9). Уравнение (8.5) — это уравнение
вида
совпадает
с искомым решением задачи (8.3). Таким
образом, дело сводится к решению уравнения
(8.5) (рис. 9). Уравнение (8.5) — это уравнение
вида
![]()
где
![]()
Оно отличается от
привычных уравнений лишь тем, что функция
![]() задана
не аналитическим выражением, а с помощью
алгоритма численного решения задачи
(8.4).
задана
не аналитическим выражением, а с помощью
алгоритма численного решения задачи
(8.4).
Для решения уравнения (8.5) можно использовать любой метод, пригодный для уточнения корней нелинейного уравнения, например, метод деления отрезка пополам, метод Ньютона (касательных) и др. Метод Ньютона здесь предпочтительнее (если имеется достаточно хорошее начальное приближение) из-за высокой стоимости вычисления одного значения функции F() (нужно решить задачу Коши (8.4) с данным ).
Метод стрельбы, сводящий решение краевой
задачи (8.3) к вычислению решений задачи
Коши (8.4), хорошо работает в том случае,
если решение
![]() «не
слишком сильно» зависит от.
В противном случае он становится
вычислительно неустойчивым, даже если
решение задачи (8.3) зависит от входных
данных «умеренно».
«не
слишком сильно» зависит от.
В противном случае он становится
вычислительно неустойчивым, даже если
решение задачи (8.3) зависит от входных
данных «умеренно».
При решении уравнений
![]() методом
деления отрезка пополам, мы задаем
методом
деления отрезка пополам, мы задаем
![]() и
и
![]() так,
чтобы разности
так,
чтобы разности
![]() и
и
![]() имели
разные знаки. Затем полагаем
имели
разные знаки. Затем полагаем
![]()
Вычисляем
![]() Затем
вычисляем
Затем
вычисляем
![]() по
одной из формул:
по
одной из формул:
![]() или
или
![]()
в зависимости от того, имеют ли разности
![]() и
и
![]() соответственно
разные или одинаковые знаки. Затем
вычисляем
соответственно
разные или одинаковые знаки. Затем
вычисляем
![]() Процесс
продолжаем до тех пор, пока не будет
достигнута требуемая точность
Процесс
продолжаем до тех пор, пока не будет
достигнута требуемая точность
![]()
В случае использования для решения
уравнения
![]() метода
Ньютона задаем
метода
Ньютона задаем
![]() а
затем последующие
а
затем последующие
![]() вычисляем
по рекуррентной формуле
вычисляем
по рекуррентной формуле
![]() n = 0,
1, …
n = 0,
1, …
Производная
![]() может
быть вычислена по одной из формул
численного дифференцирования, например,
первого порядка аппроксимации:
может
быть вычислена по одной из формул
численного дифференцирования, например,
первого порядка аппроксимации:
![]()
2.7. Вычислительная неустойчивость задачи Коши
Поясним причину возникновения вычислительной неустойчивости на примере следующей линейной краевой задачи:
![]()
![]()
![]()
![]() (8.6)
(8.6)
при постоянном
![]() Выпишем
решение этой задачи:
Выпишем
решение этой задачи:
![]()
Коэффициенты при
![]() и
и
![]() с
ростомростаются ограниченными на
отрезке
с
ростомростаются ограниченными на
отрезке
![]() функциями;
при всех
функциями;
при всех
![]() они
не превосходят единицу. Поэтому небольшие
ошибки при задании
они
не превосходят единицу. Поэтому небольшие
ошибки при задании
![]() и
и
![]() ведут
к столь же небольшим погрешностям в
решении, т. е. краевая задача является
«хорошей».
ведут
к столь же небольшим погрешностям в
решении, т. е. краевая задача является
«хорошей».
Рассмотрим теперь задачу Коши:
![]()
![]()
![]()
![]() (8.7)
(8.7)
Ее решение имеет вид:
![]()
Если при задании
![]() допущена
погрешность, то
значение решения при
допущена
погрешность, то
значение решения при
![]() получит
приращение
получит
приращение
![]() (8.8)
(8.8)
При больших рвычитаемое в равенстве
(8.8) пренебрежимо мало, но коэффициент
в первом слагаемом
![]() становится
большим. Поэтому метод стрельбы при
решении задачи (8.6), будучи формально
приемлемой процедурой, при больших р
становится практически непригодным.
Подробнее о возникновении неустойчивостей
см. [1, 2].
становится
большим. Поэтому метод стрельбы при
решении задачи (8.6), будучи формально
приемлемой процедурой, при больших р
становится практически непригодным.
Подробнее о возникновении неустойчивостей
см. [1, 2].
