67) Классическое вероятностное пространство

Вероятностное пространство — это тройка , где

• —это произвольное множество, элементы которого называются элементарными событиями, исходами или точками;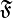

• —сигма-алгебра подмножеств 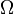, называемых (случайными) событиями;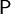

• —вероятностная мера или вероятность, т.е. сигма-аддитивная конечная мера, такая что

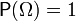
Классический способ задания вероятностей — такой способ задания вероятностей, когда количество элементарных исходов конечно и все они имеют одинаковую вероятность. Тогда вероятность любого события определяется как отношение его мощности (т.е. количества элементарных исходов, благоприятствующих данному событию) к общему числу элементарных исходов:

.

68) Теоремы сложения, умножения вероятностей. Несовместные, независимые события

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

Следствие 1: Если события  образуют полную группу несовместных событий, то сумма их вероятностей равна единице.

Определение. Несовместными называются два противоположных события, образующие полную группу.

Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.

Следствие 2: Сумма вероятностей противоположных событий равна единице.

Определение. Событие А называется независимым от события В, вероятность события А не зависит от того, произошло событие В или нет. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Теорема Умножения вероятностей: Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило.

69) Формулы полной вероятности и Байеса. Примеры

Пусть некоторое событие А может произойти  вместе с одним из несовместных событий , составляющих полную группу событий. Пусть известны вероятности этих событий  и условные вероятности наступления события А при наступлении события H_i .

Теорема. Вероятность события А, которое может произойти вместе с одним из событий , равна сумме парных произведений вероятностей каждого из этих событий на соответствующие им условные вероятности наступления события А.

Ф-ла Байеса: Пусть имеется полная группа несовместных гипотез  с известными вероятностями их наступления . Пусть в результате опыта наступило событие А, условные вероятности которого по каждой из гипотез известны, т.е. известны вероятности.

Требуется определить какие вероятности имеют гипотезы относительно события А, т.е. условные вероятности.

Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события.

70)Аксиоматическое построение теории вероятностей. Следствия из аксиом

Аксиома 1: Каждому случайному событию А поставлено в соответствие неотрицательное число Р(А), называемое его вероятностью

Аксиома 2:

Аксиома 3: Если события ААА попарно несовместимы, то

Из сформулированных аксиом можно вывести несколько важных элементарных следствий:

Из 1-й:

Из 3-й:

Таким образом:

1) Вероятность невозможного события равна нулю

2) Для любого события А

3) Каково бы ни было случайное событие А

4) Если событие А влечёт за собой событие В, то

5) Пусть А и В — два произвольных события. Т. к.  в суммах А + В = А + (В – АВ) и В = АВ + (В – АВ) слагаемые являются несовместимыми событиями, то в соответствии с аксиомой 3:

Р(А + В) = Р(А) + Р(В – АВ); Р(В) = Р(АВ) + Р(В – АВ)

Отсюда вытекает теорема сложения для произвольных событий А и В:

Р(А + В) = Р(А) + Р(В) – Р(АВ)

В силу неотрицительности Р(АВ) отсюда заключаем, что

Р(А + В) 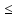Р(А) + Р(В)

71. Случайная величина называется Дискретной , если множество ( x1 ,x2 …….. Xm……..) её возможных значений конечно или счётно ( т.е. если все её значения можно перечислить).При решении задач на составление ряда распределения дискретной СВ нужно отвечать на следующие вопросы:Каковы возможные значения этой СВ?В чём заключается событие ( пси = Х₀?Как определить вероятность таких событий?Дискретная СВ (пси) имеет Распределение Пуасона с параметром a, если она принимает значения 0, 1, 2……., m ……. . Закон распределения Пуасона является хорошим приближением для биномиального распределения при больших значениях n и p ( или 1 – p).СВ (пси) имеет Бинамиальное распределение с параметрами n и p , если она принимает значения 0 , 1 , ……. n с вероятностями P( пси = m)= C_n^m p^mq^n-m, m = 0 1 2 …… , n, где 0<p<1 , q = 1 –p .

72. СВ называется Непрерывной,если её функция распределения непрерывна на всей числовой оси . Непрерывная СВ принимает все значения из некоторого интервала или системы интервалов на числовой оси.1)Непрерывная СВ (пси) имеет Равномерное распределение на отрезке (А:B), если её плотность распределения постоянна на этом отрезке, а вне его равна нулю:

P(х) = 1/b-a при x € [a;b]

P(х) = 0 при Х не принадлежит [а,б]

2)Непрерывная СВ( пси) имеет Показательное (экспоненциальное) распределение с параметром Лямда > 0 , если её плотность распределения имеет вид: P(х) = лямда e ^{–лямда х} при Х≥0

P(х) = 0 при Х < 0.

73. Функции распределения случайной величины и её свойства. Определение случайной величины.

Функция распределения представляет собой универсальный способ задания СВ в том смысле ,что она существует для любой СВ. Ряд распределения существует только для дискретной СВ, а плотность распределения ----- только для непрерывной. Для непрерывной СВ функция распределения F(х) = P((пси)<х) непрерывна в любой точке числовой прямой. Более того, P((пси)=х₀)=0, т.е вероятность того , что непрерывная СВ примет заранее указанное значение, равна нулю.( Заметим , однако, что это событие не обязательно невозможно.) Отсюда следует, что для непрерывной СВ P (α ≤ (пси) ≤ β) = P(α < (пси) ≤ β) = P(α< (пси) <β) = P(α ≤ (пси)) <β = F(β) – F(α).

74. Свойство плотности распределения случайной величины. Примеры. Ряд распределения. Функцию p(x) будем называть Плотностью распределения СВ (пси), если вероятность того , что (пси) принимает значения из промежутка (-∞; х) равна интегралу от этой функции в пределах от -∞ до х , т.е F(x) = P( (пси) < x) = 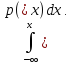Следовательно если функцияp(x) непрерывна в точке х, то функция распределения F(x) дифференцируема в этой точке, причём p(x) = F(x). Свойства плотности распределения .1. p(x) ≥ 0 при всех Х , т.к F(x) ----- неубывающая функция. 2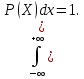Вероятность попадания непрерывной СВ (пси) в интервал , отрезок или полуинтервал с одними и теми же концами одинаковы и равны определённому интегралу от плотности вероятности на этом промежутке :P (α ≤ (пси) ≤ β) = P(α < (пси) ≤ β) = P(α< (пси) <β) =

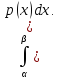
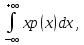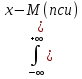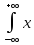75. Математическое ожидание М(пси) и дисперсия D(пси) непрерывной СВ (пси) определяется по формулам M(пси) = D(пси) =²p(x)dx. На практике вычесления дисперсии, как правило , удобно использовать формулу M(пси²) = ²p(x) dx.

Свойства: 1. Математическое ожидание постоянной С равно этой постоянной.     2. Постоянный множитель можно выносить за знак математического ожидания, т.е. 3. Математическое ожидание суммы нескольких случайных величин равно сумме математических величин: 4. Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий этих величин **:

76. Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.1°. Дисперсия постоянной равна нулю. 2°. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

3. Если и-независимые случайные величины , то дисперсия суммы этих величин равна сумме их дисперсий:

4. Дисперсия любой случайной величины неотрицательна: Среднеквадратическим отклонением  случайной величины Х называется квадратный корень из дисперсии.

77. Числовые характеристики СВ:

1. Дисперсия; 2. Мат. ожидание; 3. Начальный; 4. Центральный момент.

Начальным моментом k-го порядка случайной величины x называется математическое ожидание k-й степени случайной величины x , т.е. a _k = Mx ^k.

Центральным моментом k-го порядка случайной величины x называется величина m _k, определяемая формулой m _k = M(x - Mx )^k.

Заметим, что математическое ожидание случайной величины - начальный момент первого порядка, a ₁ = Mx , а дисперсия - центральный момент второго порядка,

a ₂ = Mx ² = M(x - Mx )² = Dx .

78. Нормальное распределение (распределение Гаусса) — распределение вероятностей, которое задается функцией плотности распределения:

Правило трех сигм: Вероятность того, что случайная величина отклонится от своего математического ожидания на большую величину, чем утроенное среднее квадратичное отклонение, практически равна нулю. практически все значения нормально распределённой случайной величины лежат в интервале .

79.Схема Бернулли.Под схемой Бернулли понимают конечную серию повторных независимых испытаний с двумя исходами. Вероятность появления (удачи) одного исхода при одном испытании обозначают , а непоявления (неудачи) его . Я. Бернулли установил, что вероятность ровно успехов в серии из  повторных независимых испытаний вычисляется по следующей формуле: То значение , при котором число является максимальным из множества {}, называется наивероятнейшим, и оно удовлетворяет условию

np-q ≤ m₀≤ np+p, (m₀ € Z)

Формулу Бернулли можно обобщить на случай, когда при каждом испытании происходит одно и только одно из k событий с вероятностью p_i(1,2,…k). Вероятность появления m₁ раз первого события и m₂ - второго и m_k –k-го находится по формуле

При достаточно большой серии испытаний формула Бернулли становится трудно применимой, и в этих случаях используют приближенные формулы. Одну из них можно получить из предельной теоремы Пуассона: