m1var16

Вариант № 16

1. Найти область определения функции : y = 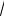sin x + 16 − x2 .

Область определения данной функции определяется двумя неравенствами:

16 − x2 ≥ 0

и

sin x ≥ 0 .

Из

второго

неравенства

следует,

что

должно

выполняться

неравенство 2kπ ≤ x ≤ (2k +1)π , где

k

– любое

целое

число. Из

первого

неравенства

находим, что

16 − x2

≥ 0, если − 4 ≤ x ≤ 4 . При k = −1 получим x [−4, − π ]. При k = 0

получим x [0, π ]. При других значениях k

неравенства не имеют общих рещений.

Ответ: x [−4, − π ] [0,π ].

2. Построить график функции: y = x +1.

x −1

Данная функция определена на всей числовой оси,

кроме точек

x = 1

и

x = −1. Преобразуем функцию:

8

y = x +1

если

x ≥ 0

и

y =

− x +1

если

x < 0. Или

x −1

− x −1

4

y = x −1+ 2 = 1+

2

. Функция чётная, прямая

y = 1

4

2

0

2

4

x −1

x −

1

является

горизонтальной

асимптотой.

Достаточно

4

построить

график

(по

точкам)

для

x ≥ 0,

затем

отобразить полученную часть графика зеркально

8

относительно оси ОУ.

Ответ: График представлен на рисунке.

3. Построить график функции: y = arctg(4x −1).

Область определения функции – вся числовая ось: x (−∞, ∞) . Преобразуем функцию:

y = arctg(4x −1) = arctg[4(x −1/ 4)]. Строим сначала

arctg x . Затем «сжимаем» график в

четыре раза

по

оси

ОХ

и

сдвигаем

его

по оси

ОХ

на

четверть

единицы

вправо.

2

2

2

1

1

1

3

1.5

0

1.5

3

3

1.5

0

1.5

3

2

1

0

1

2

1

1

1

2

2

2

Получим график данной функции. Ответ: Последовательность построения представлена на рисунках.

x = cost

4. Построить график функции: y =

.

4

y = π sint

Исключим параметр t: y = π sint = ±π

1− cos2

t . Или

2

y = ±π

1− x2 . Преобразуя, получим уравнение эллипса с

центром

в начале координат, с

малой полуосью

1 и с

2

1

0

1

2

большой полуосью π : x2 + y2 /π 2

= 1.

2

Ответ: График представлен на рисунке.

5. Построить график функции: ρ = 1− cosϕ .

4

Поскольку ρ ≥ 0, то функция существует для тех

значений φ, для которых cosϕ ≤ 1. Это наблюдается при

90

всех значениях φ. Функция возрастает от 0 до 2 (при

ϕ = π ),

затем убывает

от

2 до

0.

Вертикальная

ось

пересекается графиком

в

точках

(π/2, 1)

и (3π/2,

1).

180

0

Можно

перейти

к декартовым

координатам.

Тогда

0

1

2

получим

уравнение

x2

+ y2 =

x2

+ y2 ) − x .

Ответ:

график представлен на рисунке.

270

6. Вычислить предел: lim

(n + 6)3 − (n

+1)3

.

+ (n + 4)2

n→∞ (2n + 3)2

Возведём все скобки в степени и приведём подобные:

(n

+

6)3 − (n +1)3

=

∞

= lim

n3 +18n2

+108n + 216 − n3

− 3n2 − 3n −1

=

lim

+ 3)2 + (n +

4n2 +12n + 9 + n2 +

8n +16

n→∞ (2n

4)2

∞

n→∞

15n2 +105n + 215

3 + 21n

−1 + 43n−2

(n + 6)3

− (n +1)3

= lim

= lim

=

3. Ответ: lim

= 3.

−1 +

5n−2

+ (n +

4)2

n→∞ 5n2 + 20n + 25

n→∞ 1+ 4n

n→∞ (2n + 3)2

7. Вычислить предел: lim

x3

− x2 − x +1

(неопределённость вида (0/0)).

x3 − 3x + 2

x→1

Разлагаем числитель и знаменатель на простые множители: lim

x3 − x2

− x +1

=

x3 − 3x +

x→1

2

= lim

(x

−1)2 (x +1)

= lim

x +

1

=

2

. Ответ: lim

x3 − x2 − x +1

=

2

.

x3 − 3x + 2

x→1 (x

−1)2 (x + 2) x→1 x +

2 3

x→1

3

3

x − 6 + 2

8. Вычислить предел: lim

(неопределённость вида (0/0)).

x + 2

x→−2

Вычислим

предел,

используя

замену

переменной:

x − 6 = t3 , если

x → −2,

lim

3 x − 6 + 2

=

= lim

t + 2

= lim

t + 2

=

+ 2

t → −2

+ 2)(t2 − 2t + 4)

x→−2

x

то

t→−2 t3 + 8

t→−2 (t

= lim

1

=

1

3

x −

6 + 2

=

1

. Ответ: lim

.

x + 2

t→−2 t2

− 2t + 4 12

x→−2

12

9. Вычислить предел: lim

cos3x −1

(неопределённость вида (0/0)).

x→0

xtg 2x

Воспользуемся

формулой

1− cos x = 2sin2

x

и

первым

замечательным

пределом:

2

3x

x

sin x

cos3x

−1

2sin2 (3x / 2)cos2x

9

sin

sin

2x

lim

= 1:

lim

= −lim

= −

lim

2

2

=

x→0

x

x→0

xtg 2x

x→0

xsin 2x

4 x→0

3x / 2

3x / 2 sin 2x

9

sin(3x / 2)

2

sin 2x

−1

9

cos3x −1

9

−

lim

(lim

)

= −

Ответ:

lim

= −

.

4

x→0

3x / 2

x→0

2x

4

x→0

xtg 2x

4

2n2

+ 7n −1

n

10. Вычислить предел: lim

(неопределённость вида (1∞)).

2

2n

+ 3n −1

n→∞

Приведём

предел

ко

второму

замечательному

пределу:

+

1 z

= e:

lim 1

z→∞

z

2n

2

n

2n

2

+ 3n −1

+

4n

n

4n

n

2

+ 7n −1

2

=

lim

+ 3n

= lim

2n

2

+ 3n −1

= lim 1+

2n

n→∞ 2n

−1

n→∞

n→∞

+ 3n −1

4n2

lim

2n2+3n−1

4n2

2n2

+3n−1 n→∞ 2n2+3n−1

4n

4n

2n2 +3n−1

=

+

4n

4n

= e

2

,

так

как

= lim 1+

lim 1

n→∞

2n

2

+ 3n −1

2n

2

+ 3n −1

n→∞

lim

4n2

2n2

+ 7n −1 n

= e2 .

2

= 2 . Ответ: lim

2

n→∞ 2n

+ 3n −1

2n

n→∞

+ 3n −1

11. Вычислить предел: lim

eπ

− ex

(неопределённость вида (0/0)).

− sin3x

x→π sin 5x

Сделаем замену переменной,

затем

воспользуемся

эквивалентными

величинами:

x − π = t, x = t + π , если x → π , то t → 0. Тогда lim

eπ

− ex

=

x→π sin5x − sin3x

= lim

eπ − et+π

= lim

eπ (et −1)

= et

−1 ~ t,

eπ t

=

e

π

sin(5t +

5π ) − sin(3t +

sin at ~ at = lim

− 3t

|

t→0

3π ) t→0

sin5t − sin3t

t→0 5t

2

Ответ: lim

eπ

− ex

=

eπ

.

x→π sin 5x − sin3x

2

1

12. Исследовать функцию на непрерывность и построить эскиз графика: y = 2x(x−1) .

Область определения: x (−∞, 0) (0,1) (1, ∞). В области определения функция

является непрерывной (как элементарная функция). Исследуем поведение функции в

граничных

точках

области

определения:

1

1

1

1

lim 2x(x−1) = 2∞ = ∞,

lim 2x(x−1)

= 2−∞

= 0, lim 2x(x−1)

= 2−∞ = 0, lim 2x(x−1)

= 2∞ = ∞ . Таким

x→0−0

x→0+0

x→1−0

x→1+0

образом, в точках x=0 и x=1 функция имеет разрывы второго рода. Для построения эскиза

1

графика

функции

рассмотрим

поведение

функции

в

бесконечности:

lim 2x(x−1)

=

x→−∞

1

= lim 2x(x−1)

= 20

= 1.

x→+∞

Ответ: В точках x=0

8

1

и x=1 функция имеет

разрывы

второго

рода,

в

4

0.75

остальных

точках

она

0.5

непрерывна.

Эскиз

2

1

0

1

2

графика

представлен

на

4

0.25

рисунках.

На

втором

рисунке

показано

8

1

0.5

0

0.5

1

поведение

функции

в

интервале (0, 1) в более крупном масштабе.

13.

Исследовать

функцию

на

непрерывность

и

построить

эскиз

графика:

x2

+1,

x ≤ 1,

y =

> 1.

.

x −1,

x

Область определения функции: x (−∞,∞) . Ось ОХ разбивается на два интервала,
на каждом из которых функция f(x) совпадает с одной из указанных непрерывных
функций. Поэтому точкой разрыва может быть только
точка,	разделяющая	интервалы.		Вычислим		2
односторонние пределы:
lim f (x) = lim (x2 +1) = 2,		lim	f (x) = lim (x −1) = 0,			1.5
x→1−0	x→1−0	x→1+0	x→1+0
. Таким образом, в точке x=1 функция терпит разрыв						1
первого	рода. Величина скачка		функции в	точке x=1
равна -2.						0.5
Ответ: В точке x=1 функция имеет разрыв первого рода,
в остальных точках она непрерывна. Эскиз графика					1	0	1	2
представлен на рисунке.

14. Исходя из определения производной, найти f ′(0):

f (x) = x2 cos2 (11/ x), x ≠ 0,

f (0) = 0 .

По определению

f ′(x0) =lim

f (x0 + x) − f (x0 )

. Заменим x на x-x0:

x→0

x

f ′(x

)

= lim

f (x) − f (x0 )

. Но x

= 0, f (x

) = 0,

поэтому f ′(0) = lim

f (x)

. В данном

0

x→x0

x

− x0

0

0

x→0

x

случае

f ′(0) = lim

x2 cos2 (11/ x)

= lim[x cos2 (11/ x)] = 0, так как

cos(11/ x)

≤ 1 всегда.

x→0

x

x→0

Ответ: f ′(0) = 0 .

15. Найти производную показательно-степенной функции: y = xsin x3

. Прологарифмируем

функцию: ln y = sin x3 ln x . Берём

производную,

как производную неявной функции:

y′

= 3x2 cos x3 ln x +

sin x3

. Подставляем сюда y: y′ = (3x2 cos x3 ln x +

sin x3

) xsin x3 .

y

x

x

Ответ:

y′ = (3x2 cos x3 ln x +

sin x3

) xsin x3 .

x

16. Составить уравнения касательной и нормали к кривой в данной точке, вычислить y′′ :
				xx
x = tsin t + cost	t =	π
		.
y = sint − t cost		3
Уравнения	касательной		и нормали к кривой	y = f (x) имеют вид
y = y0 + y′x (x0 ) (x − x0 ) и y = y0			− (1/ y′x (x0 )) (x − x0 ) , где x0 и	y0 - координаты точки

касания. Вычислим сначала эти координаты:

x

= x(π /3) = 1 +

π

, y

0

= y

(π /3) =

3 − π .

Найдём

0

2

2

3

2

6

5

производные y′

и y′′ :

y′ =

yt′

=

x

xx

x

x′

2.5

t

= cost − cost + tsin t

= tg t .Тогда

y′

(π /3) =

3 .

Далее,

5

2.5

0

2.5

5

sint + t cost − sin t

x

y ′ = (y′x )′t

= −

(tg t)′

=

2.5

x

xt′

(tsint + cost)′

5

=

1

=

1

,

следовательно,

cos2 t (sint + t cost − sin t))

t cos3

t

y ′(π /3) =	24												касательной y =						3		− π +		(x −			1	−	π
		. Таким			образом,				уравнение													3									) ,
x	π												2 6											2				2	3
урав-
					− π −							π
нение нормали y =			3			1			(x −	1	−
															). Или 3 3x − 3y − 2π = 0 и x +									3y − 2 = 0 .
		2			6	3			2			2	3

Ответ:

π

π

1

3

(x

, y

) =

+

,

−

, y′

(x

) = 3,

0

0

2

2

6

x

0

2

3

24

3x − 3y − 2π = 0

касательная

yx′(x0 )

=

3

,

.

π

+

3y − 2 = 0

нормаль

x

17.

Функция y(x), заданная неявно уравнением x2 + xsin y − ey = 3, принимает в точке

x

0

= 2 значение y

0

= 0. Найти

y′ , y

′′

, y′

(x

0

), y′′

(x

0

) .

x

xx

x

xx

Дифференцируем

уравнение

по

x,

предполагая,

что

y=

y(x):

2x + sin y + xy′cos y − ey y′ = 0 . Из этого равенства находим: y′ = −

2x + sin y

. Находим

xcos y − ey

вторую производную:

y ′ = −

(2 + y′cos y)(xcos y − ey ) − (cos y − xy′sin y − ey y′)(2x + sin y)

.

(xcos y − ey )2

Вычислим производные в точке: x

= 2

y′(2) = −4,

y′′(2) = 22 . Ответ: y′ = −

2x + sin y

,

0

xcos y − ey

y ′ = −

(2 + y′cos y)(xcos y − ey ) − (cos y − xy′sin y − ey y′)(2x + sin y)

,

y′(2) = −4,

y′′(2) = 22 .

(xcos y − ey )2

18. Вычислить приближённое значение функции в заданной точке с помощью

дифференциала:	y = x	7 , x = 2,002 .
По определению		дифференциала y(x0 + x) = y(x0 ) + dy(x0 ) + o( x) или, в других
обозначениях,	y(x) = y(x0 ) + dy(x0 ) + o((x − x0 )), x = dx = x − x0 . Отсюда получаем

формулу для приближённых вычислений:

y(x) ≈ y(x0 ) + y′(x0 )(x − x0 ). В данном случае

x

0

= 2,

y(x

0

) = y(2) = 128,

y′ = 7x6 , y′(x

0

)

= y′(2)

= 448,

x = 0,002 .

Тогда

y(2,002) ≈ 128 + 448 0,002 = 128,896. Ответ: y ≈ 128,896

19. Вычислить предел с помощью правила Лопиталя:

lim

(2x +1)ln−1(1−e−2x−1) .

x→−1/ 2+0

Это неопределённость вида (00). Преобразуем предел:

(2x +1)ln−1(1−e−2x−1)

=

lim

[ln−1(1−e−2x−1) ln(2 x+1)]

lim

lim

eln−1(1−e−2x−1) ln(2 x+1) = ex→−1/ 2+0

.

Найдём

x→−1/ 2+0

x→−1/ 2+0

ln(2 x

+1)

=

∞

=

(ln(2 x +1))′

=

предел в показателе степени:

lim

lim

x→−1/2+0 ln(1

− e

−2x−1)

∞

x→−1/2+0 (ln(1− e−2x−1))′

=

lim

2(1− e−2x−1 )

=

lim

2e−2x−1

=

lim

1

= 1.

x→−1/ 2+0 2(2 x +1)e−2x−1

x→−1/ 2+0 2e−2x−1 + 2(2x +1)e

−2x−1

x→−1/ 2+0 2(x +

1)

Следовательно,

lim

(2x +1)ln−1(1−e−2x−1)

= e1 = e . Ответ:

lim (2x +1)ln−1(1−e−2x−1)

= e .

x→−1/ 2+0

x→−1/ 2+0

20. Вычислить предел с помощью правила Лопиталя: lim(

1

−

π

).

x→π

sin x

π − x

1

π

π

− x − π sin x

0

Это неопределённость вида (∞−∞): lim(

−

) = lim

=

=

π

x→π sin x

− x

x→π

(π − x)sin x

0

= lim

−1− π cos x

= ∞ . Ответ: lim(

1

−

π

) = ∞ .

− sin x + (π − x)cos x

x→π

x→π

sin x

π − x

21. Многочлен

по

степеням

x

представить в

виде

многочлена

по степеням

(x − x0 ) :

f (x) = x4 − 3x3 , x

0

= 2 .

Запишем

формулу

Тейлора

для

многочлена

четвёртой

степени:

f (x) = f (x

) + f ′(x

)(x − x

) +

f ′(x0 )

(x − x

)2 +

f

′(x0 )

(x − x

)3

+

f (4) (x0 )

(x − x

)4 .

0

0

0

0

0

0

2!

3!

4!

Найдём

все

производные:

f ′(x) = 4x3 − 9x2 , f ′(x) = 12x2

−18x, f ′(x) = 24x −18 ,

f (4) (x) = 24 . Тогда

f (2) = −8,

f ′(2) = −4, f ′(2) = 12,

f ′(2) = 30,

f (4) (2) = 24 . Подставив

это в формулу, получим: f (x) = −8 − 4(x − 2) + 6(x − 2)2 + 5(x − 2)3 + (x − 2)4 .

Ответ: f (x) = −8 − 4(x − 2) + 6(x − 2)2 + 5(x − 2)3

+ (x − 2)4 .

22. Найти многочлен, приближающий заданную функцию f (x) в окрестности точки x0 с

точностью до o((x − x

0

)3 ) :

f (x) = sin ln x, x

0

= eπ / 6 .

Применяем формулу Тейлора:

f (x) = f (x

) + f ′(x

)(x − x

) +

f ′′(x0 )

(x − x

)2

+

f ′′′(x0 )

(x − x

)3

+ o((x − x

)3 ) .

0

0

0

0

0

0

2!

3!

Вычисляем последовательно: f (eπ / 6 ) = 1/ 2,

f ′(x) = x−1 cosln x,

f ′(eπ / 6 ) = e−π / 6

/ 2,

3

f ′(x) = −x−2 cosln x − x−2 sin ln x = −x−2 (sin ln x + cosln x),

f ′(eπ / 6 ) = −e−π / 3 (

3 +1) / 2,

f ′(x) = 2x−3 (sin ln x + cosln x) + x−3 (sin ln x − cosln x), f

′(eπ / 6 ) = e−π / 2 (3 +

3) / 2.

Ответ:

			e−π / 6			(x − eπ / 6 ) −	e−π / 3 (		+1)	(x − eπ / 6 )2+	e−π / 2 (3+
f (x) =	1	+		3				3				3)		(x − eπ / 6 )3+ o((x − eeπ / 6 )3 )
2		2		4				12

23. Исследовать поведение функции в окрестности точки с помощью формулы Тейлора:

f (x) = ln(x + 3) − sin(x + 2) + x2 / 2 + 2x, x

0

= −2 .

Найдём значения функции и её первых трёх производных в заданной точке:

f (−2) = −2, f ′(x) =

1

− cos(x + 2) + x + 2,

f ′(−2) = 0,

f ′(x) = −

1

+ sin(x + 2) +1,

x

+ 3

(x +

3)2

f ′(−2) = 0, f ′(x) =

2

+ cos(x + 2),

f

′(−2) = 3.

По

формуле

Тейлора

(x + 3)3

f (x) = −2 + (x + 2)3 / 2

+ o((x + 2)3 ). Ответ: В окрестности точки

(-2,

-2) функция ведёт

себя как степенная функция третьей степени. Точка (-2, -2) является точкой перегиба: слева - интервал выпуклости, справа - интервал вогнутости.

1

− cos(

3

24. Вычислить предел с помощью формулы Тейлора: lim

2x) / x

.

x→0

1+ x2

По формуле Тейлора

1

= 1− x2 + x4 + o(x3 ) . Далее,

1+ x2

x4

1

cos( 2x) = 1− x

2

+

+ o(x

4

3

=

). Подставим это в предел: lim

− cos( 2x) / x

+ x2

6

x→0

1

1

x4

x4

o(x3 )

= lim

(1− x2

+ x4

−1+ x2

−

+ o(x3 )) = lim(

−

)

= 0 .

3

6

3

x

3

x→0 x

x→0 6x

1

− cos(

/ x

3

= 0 .

Ответ: lim

+ x2

2x)

x→0

1

25. Найти асимптоты и построить эскиз графика

функции: y = ln x − 5 + 2 .

6

x

Область

определения

функции:

4

x − 5 > 0 x > 5, x < 0 x (−∞, 0) (5, ∞).

x

2

Функция непрерывна в каждой точке области

определения. Найдём односторонние пределы в

граничных

точках

области

определения:

10

5

0

5

10

15

x − 5

= ∞,

x

− 5

+

lim ln

+ 2

lim ln

2 = ∞ .

2

x→−0−0

x

x→5+0

x

Отсюда

следует,

что

прямые

x = 0

и

x = 5

являются

вертикальными

асимптотами.

Исследуем

функцию

при

x → ±∞ :

x −

5

x − 5

,

так

как

x − 5

= ln1

= 0

. Следовательно,

lim ln

+ 2 = lim ln

+ 2 = 2

limln

x→−∞

x

x→∞

x

x→∞

x

прямая

y = 1

является горизонтальной асимптотой. Очевидно, что других асимптот нет.

Ответ: Эскиз графика представлен на рисунке.

26. Провести полное исследование поведения функции и построить её график:

1

y = −xe2x2 .

1. Область определения: x (−∞, 0) (0, ∞). 2. Функция нечётна, периодичность отсутствует. 3. Функция имеет разрыв в точке x = 0. Исследуем поведение функции в окрестности точки разрыва:

1

1

t

2

1

t

2

1

2x2

1/ x = t,

e

e

2

te

2

lim − xe2x2

= − lim

=

= − lim

= − lim

= ∞ .

x→0−0

x→0−0 1/ x

x → 0 − 0 t → −∞

t→−∞

t

t→−∞ 1

1

Аналогично,

lim − xe2x2

= −∞ . Таким образом, прямая x = 0 является вертикальной

x→0+0

асимптотой.

1

1

= ∞,

4. lim − xe2x2

lim

− xe2x

2 = −∞ . Ищем наклонные асимптоты в виде y = kx + b :

x→−∞

x→+∞

f (x)

1

1

1

k = lim

= lim − xe

2x

2

/ x

= − lim e2x2

= −1,

b = lim[ f (x) − kx] = − lim[x(e2x2 −1)] =

x

x→±∞

x→±∞

x→±∞

x→±∞

x→±∞

1

1

1

1

=

e2x2 −1 ≈

при

→ 0

= − lim[x

] = 0. Следовательно, прямая

y = −x

2x2

2x2

2x2

x→±∞

является наклонной асимптотой.

1

1

1

1

− x2

1

5. Первая производная y′ = [−xe2x2 ]′ = −e2x2

+ x−2 e

2x2

=

e2x2 . Производная

x2

обращается в нуль в точках x = −1 и x = 1. При x < −1 производная	отрицательна, при
−1 < x < 0 производная положительна. Следовательно, точка x = −1	является точкой

минимума, причём f (−1) = e . При 0 < x < 1 производная положительна, при x > 1

производная отрицательна. Следовательно, точка x = 1 является точкой максимума,

причём

f (1) = −

e .

6. Вторая производная:

1

− x2

12

′

− 2x3 − 2x(1− x2 )

1

2

−

6

y ′ =

x2

e2x

=

x4

e2x

3

− 1− x2

1

1

e2x2

x−3

= −

1+ x2 e2x2 . Вторая

x2

x5

6

3

0

3

6

производная в нуль не обращается. В точке x = 0

вторая производная не существует. Имеем два

3

интервала: интервал

(−∞, 0) и интервал (0, ∞).

Производная y′′ > 0 при x (−∞, 0) и y′′ < 0 при

6

x (0, ∞) . Следовательно, в интервале (−∞, 0)

график функции вогнутый, а в интервале (0, ∞) - выпуклый. Точек перегиба нет. 7.

График функции не пересекает осей координат. Ответ: График функции представлен на

рисунке, минимум функции - в точке (−1,

e) , максимум функции – в точке (1, −

e) .