§ 7.4 Собственные векторы и собственные значения линейного оператора

Пусть - линейный оператор, действующий в линейном пространстве над полем , имеет в некотором базисе этого пространства матрицу .

Вектор , удовлетворяющий соотношению

, (7.4.1)

называется собственным вектором, а соответствующее число - собственным значением линейного оператора .

В комплексном линейном пространстве всякий линейный оператор имеет хотя бы один собственный вектор.

В матричной форме равенство (7.4.1) принимает вид . Отсюда получается следующая матричная запись

(7.4.2)

системы линейных алгебраических уравнений относительно столбца координат собственного вектора , соответствующего собственному значению , которая подробно записывается в виде

Если известно собственное значение , то все собственные векторы , соответствующие этому собственному значению, находятся как ненулевые решения системы (7.4.2).

Условием существования ненулевого решения однородной системы линейных уравнений (7.4.2) является равенство нулю ее определителя

(7.4.3)

Многочлен, стоящий в левой части уравнения (7.4.3), называется характеристическим многочленом матрицы и оператора , а само уравнение (7.4.3) - характеристическим или вековым уравнением матрицы (оператора ).

Собственные значения оператора , и только они, являются корнями характеристического многочлена (принадлежащими данному полю ) матрицы оператора . Учитывая, что подобные матрицы и определяют один и тот же линейный оператор , действующий в линейном пространстве , и что они имеют один и тот же характеристический многочлен, будем отождествлять характеристический многочлен подобных матриц с характеристическим многочленом линейного оператора, определяемого этими матрицами, а его корни - с собственными значениями этого оператора.

Множество всех собственных значений линейного оператора (каждое собственное значение берется столько раз, какова его алгебраическая кратность, т.е. кратность как корня характеристического многочлена) называется спектром линейного оператора.

Собственные векторы линейного оператора , относящиеся к одному и тому же собственному значению , вместе с нулевым вектором образуют подпространство, которое называется собственным подпространством оператора, соответствующим собственному значению .

Собственные векторы линейного оператора , относящиеся к различным собственным значениям, линейно независимы.

Для отыскания всех собственных значений оператора с матрицей нужно найти все корни характеристического многочлена матрицы и из них выбрать лишь те, которые принадлежат данному полю , а для отыскания всех собственных векторов оператора с матрицей нужно найти все ненулевые решения системы (7.4.2) при каждом собственном значении .

В силу того, что на практике обычно отождествляют оператор с его матрицей, введенные в этом параграфе понятия собственного вектора, собственного значения, спектра, собственного подпространства для линейных операторов из определены также и для квадратных матриц.

Пример 1. Докажите, что если матрицы и подобны, то всякое собственное значение является собственным значением и для , и обратно. Найдите связь между собственными векторами матриц и .

Доказательство. Поскольку квадратные матрицы и подобны, существует невырожденная матрица , такая, что . Отсюда следует, что

т.е. спектры матриц и совпадают. Подчеркнем, что матрицы с одинаковыми собственными значениями не обязательно являются подобными. Действительно, матрица не подобна матрице , но обе эти матрицы имеют собственное значение 0 с алгебраической кратностью 2.

Пусть - собственный вектор матрицы , а - соответствующее собственное значение. Тогда

.

Домножая левую и правую части последнего равенства на , получаем:

или ,

где - собственный вектор матрицы , отвечающий тому же собственному значению .

Пример 2. Для оператора с матрицей , действующего в действительном пространстве, найдите собственные значения и собственные векторы.

Решение. Характеристический многочлен

матрицы имеет корни , , . Поскольку рассматриваемый оператор действует в действительном линейном пространстве, то его собственным значением будет лишь .

Для нахождения координат собственного вектора , отвечающего этому собственному значению, решим однородную систему линейных уравнений с матрицей :

.

Общим решением этой системы является . При , пробегающим все действительные значения, оно даёт общий вид собственных векторов оператора с матрицей , отвечающих собственному значению . Других действительных векторов оператор с матрицей не имеет, т.к. у него нет других собственных значений.

Рассмотренный в данном примере линейный оператор имеет единственное собственное подпространство, базис которого составляет вектор

7.4.1. Пусть - собственный вектор матрицы , отвечающий собственному значению . Покажите, что любой вектор вида , где , также представляет собой собственный вектор.

7.4.2. Докажите, что собственные значения диагональной матрицы совпадают с её диагональными элементами.

7.4.3. Найдите характеристический многочлен и собственные значения верхней треугольной матрицы .

7.4.4. Докажите, что характеристический многочлен транспонированной матрицы совпадает с характеристическим многочленом матрицы .

7.4.5. Докажите, что характеристический многочлен квазитреугольной (квазидиагональной) матрицы равен произведению характеристических многочленов диагональных клеток.

7.4.6. Покажите, что характеристический многочлен матрицы имеет вид ,

где есть след матрицы , - сумма главных миноров второго порядка и т. д.; наконец есть определитель матрицы (напоминаем, что называется главным, если он расположен в столбцах и строках одинаковыми номерами).

7.4.7. Докажите, что характеристический многочлен матрицы

равен .

7.4.8. Пользуясь задачей 7.4.7, покажите, что всякий многочлен степени со старшим коэффициентом может быть характеристическим многочленом некоторой квадратной матрицы порядка .

7.4.9. Докажите, что для невырожденности оператора необходимо и достаточно, чтобы он не имел собственного значения нуль.

7.4.10. Докажите, что:

собственные векторы линейного оператора , относящиеся к собственному значению нуль, и только они, лежат в ядре этого оператора;

собственные векторы, относящиеся к ненулевым собственным значениям, лежат в образе оператора.

7.4.11. Покажите, что при умножении оператора на ненулевое число собственные векторы не меняются, а собственные значения умножаются на это число.

7.4.12. Докажите, что оператор при любом числе имеет те же собственные векторы, что и оператор . Найдите связь между собственными значениями этих операторов.

7.4.13. Докажите, что если - собственный вектор оператора , относящийся к собственному значению , то будет собственным вектором и для оператора:

;

при любом натуральном ;

, где - любой многочлен.

Найдите соответствующие собственные значения этих операторов.

7.4.14. Докажите, что если оператор невырожден, то и имеют одни и те же собственные векторы. Найдите связь между собственными значениями этих операторов.

7.4.15. Найдите собственные значения и собственные векторы оператора дифференцирования в пространстве многочленов .

7.4.16. Пусть - собственные векторы линейного преобразования, отвечающие различным собственным значениям, а числа отличны от нуля. Докажите, что вектор не является собственным.

7.4.17. Квадратная матрица с неотрицательными элементами называется стохастической, если в каждой строке этой матрицы сумма элементов равна 1. Докажите, что стохастическая матрица имеет собственное значение единица. Найдите соответствующий собственный вектор.

7.4.18. Покажите, что оператор , действующий в - мерном пространстве , не может иметь более различных собственных значений. Если различных значений ровно , то существует базис пространства , состоящий из собственных векторов оператора .

7.4.19. Пространство является прямой суммой подпространств и . Найдите собственные значения и собственные подпространства:

оператора проектирования на параллельно ;

оператора отражения в параллельно .

7.4.20. Размерность собственного подпространства оператора , соответствующего собственному значению , называется геометрической кратностью собственного значения . Покажите, что геометрическая кратность равна дефекту оператора .

7.4.21. Какой вид имеет матрица линейного преобразования, если первые базисных векторов являются его собственными векторами?

7.4.22. Докажите, что для произвольного оператора геометрическая кратность любого собственного значения не превосходит его алгебраической кратности.

7.4.23. Докажите, что сумма собственных подпространств оператора является прямой суммой.

7.4.24. Докажите, что матрица линейного преобразования в некотором базисе тогда и только тогда диагональна, когда все векторы базиса собственные.

7.4.25. Найдите собственные значения и собственные векторы линейных операторов, заданных в некотором базисе линейного пространства: 1) над полем действительных чисел ; 2) над полем комплексных чисел матрицами :

; ; ; ;

; ; ; ; ; ;

; .
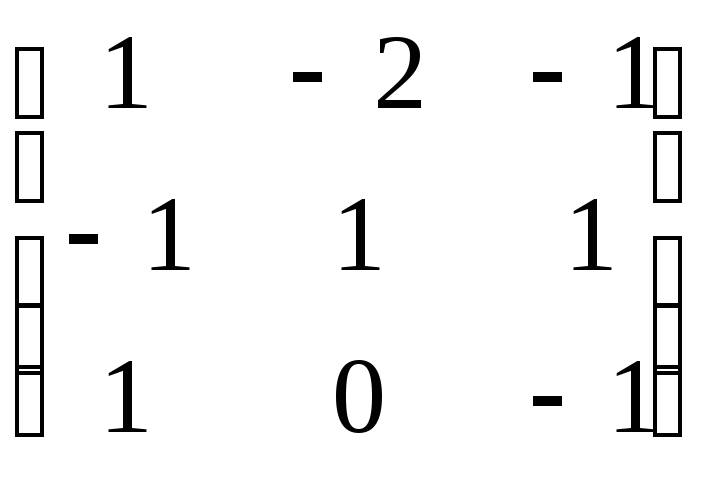
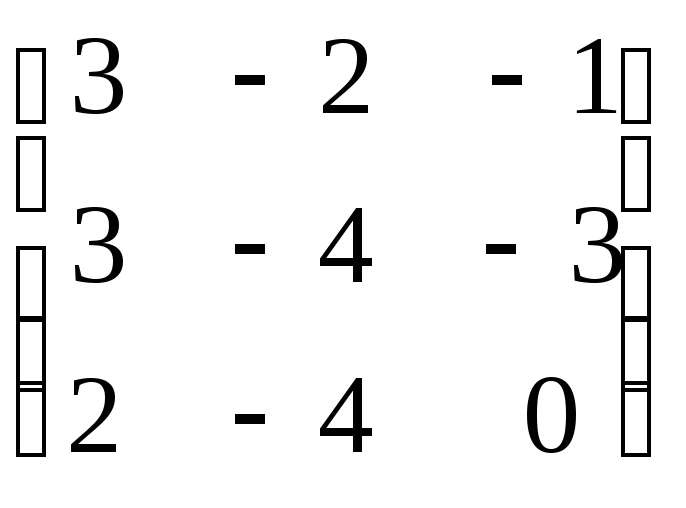