
- •Мера Лебега. Интеграл Лебега. Пространства суммируемых по Лебегу функций.
- •1.2. Мера Лебега ограниченных множеств на числовой прямой.
- •1.3. Свойства измеримых по Лебегу множеств.
- •1.4. Примеры измеримых и не измеримых подмножеств.
- •Упражнения к главе 1.
- •Глава 2. Интеграл Лебега.
- •2.1. Измеримые функции.
- •2.2. Последовательности измеримых функций.
- •Упражнение к главе 2.
- •Глава 3. Интеграл Лебега.
- •3.1. Интеграл Лебега от ограниченной функции.
- •3.2. Основные свойства интеграла Лебега.
- •3.3. Интеграл Лебега от неотрицательной измеримой функции.
- •3.4. Интеграл Лебега от произвольной измеримой функции.
- •Упражнения к главе 3.
- •Глава 4. Пространства суммируемых функций.
- •4.1. Пространство суммируемых функций.
- •4.2. Пространство функций суммируемых с квадратом.
- •4.3. Пространство функций, суммируемых со степенью p.
- •Упражнения к главе 3.
Глава 2. Интеграл Лебега.
2.1. Измеримые функции.
Символом
![]() будем обозначать расширенное множество
действительных чисел, т.е. множество
будем обозначать расширенное множество
действительных чисел, т.е. множество![]() с присоединенными несобственными
числами
с присоединенными несобственными
числами![]() и
и![]() .
.
На множестве
![]() справедливы обычные правила арифметических
действий, кроме следующих:
справедливы обычные правила арифметических
действий, кроме следующих:
Сумма двух несобственных чисел
![]() и
и![]() есть неопределенное число, также
неопределенными являются результаты
следующих операций
есть неопределенное число, также
неопределенными являются результаты
следующих операций![]() ,
,![]() .
.
Пусть
![]() - некоторое подмножество. Будем
рассматривать функции
- некоторое подмножество. Будем
рассматривать функции![]() ,
определенные на множестве
,
определенные на множестве![]() и принимающие значения в
и принимающие значения в![]() ,
т.е. функции могут принимать бесконечные
значения.
,
т.е. функции могут принимать бесконечные
значения.
Для произвольного
![]() введем множество
введем множество
![]() ,
,
называемое Лебеговым множествомфункции![]() .
.
Определение 2.1.1.Функция![]() называетсяизмеримой по Лебегу,
если
называетсяизмеримой по Лебегу,
если
множество
 измеримо;
измеримо;для любого
 множества
множества измеримы.
измеримы.
Справедлива
Теорема 2.1.1.Следующие утверждения эквивалентны
функция
 измерима;
измерима;для любого
 множество
множество измеримо;
измеримо;для любого
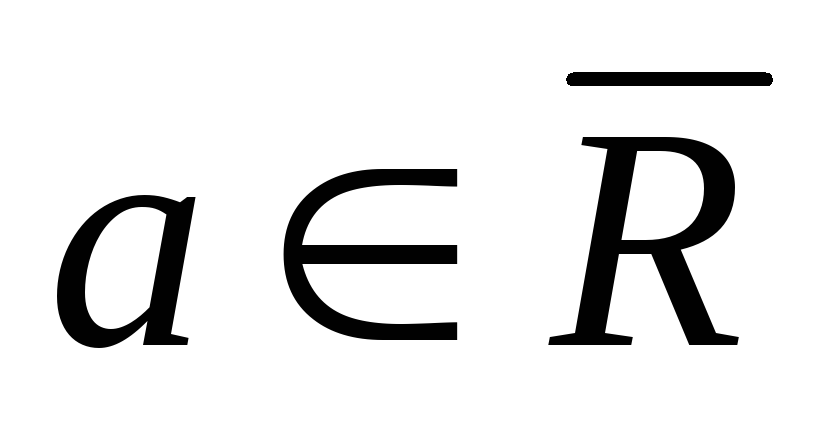 множество
множество измеримо;
измеримо;для любого
 множество
множество измеримо.
измеримо.
Доказательство.Теорема будет
полностью доказана, если будет показана
последовательность импликаций![]()
Покажем, что из первого утверждения
следует второе. Для произвольного
![]() справедливо представление
справедливо представление![]() .
В силу измеримости функции
.
В силу измеримости функции![]() ,
каждое множество
,
каждое множество![]() измеримо, а пересечение счетного числа
измеримых множеств есть измеримое
множество. Импликация
измеримо, а пересечение счетного числа
измеримых множеств есть измеримое
множество. Импликация![]() доказана.
доказана.
Докажем
![]() .
Для произвольного
.
Для произвольного![]() ,
справедливо представление
,
справедливо представление .
Отсюда следует вывод, что множество
.
Отсюда следует вывод, что множество![]() измеримо как разность двух измеримых
множеств.
измеримо как разность двух измеримых
множеств.
Импликация
![]() доказывается
аналогично утверждению
доказывается
аналогично утверждению![]() ,
используя представление
,
используя представление![]() .
Каждый элемент пересечения является
измеримым множеством, а так как элементов
пересечения счетное число, то их
пересечение есть измеримое множество.
.
Каждый элемент пересечения является
измеримым множеством, а так как элементов
пересечения счетное число, то их
пересечение есть измеримое множество.
Доказательство
![]() аналогично доказательству
аналогично доказательству![]() .
.
Теорема доказана.
Теорема 2.1.1 утверждает, что в определении
измеримой функции можно взять любое из
множеств
![]() ,
,![]() ,
,![]() ,
,![]() .
Поэтому все перечисленные множества
называютсяЛебеговыми множествамифункции
.
Поэтому все перечисленные множества
называютсяЛебеговыми множествамифункции![]() .
.
Можно показать, что для измеримой функции
![]() множества вида
множества вида![]() ,
,![]() ,
,![]() ,…измеримы
для любых
,…измеримы
для любых![]() .
При этом, из измеримости множеств
.
При этом, из измеримости множеств![]() при всех
при всех![]() не следует измеримость функции
не следует измеримость функции![]() .
.
Докажем справедливость некоторых свойств измеримых функций.
Теорема 2.1.2.Всякая функция, определенная на множестве нулевой меры, измерима.
Доказательство. Как известно, любое подмножество множества нулевой меры измеримо. Следовательно, Лебеговы множества функции имеют нулевую меру и потому измеримы.
Теорема доказана.
Теорема 2.1.3.Пусть![]() - измеримое подмножество и
- измеримое подмножество и![]() ,
,![]() ,
тогда функция
,
тогда функция![]() измерима.
измерима.
Теорема 2.1.4.Пусть![]() измерима и
измерима и![]() - измеримое подмножество. Тогда сужение
- измеримое подмножество. Тогда сужение![]() является измеримой функцией.
является измеримой функцией.
Доказательство.Справедливо равенство![]() .
Поэтому всякое Лебегово множество
функции
.
Поэтому всякое Лебегово множество
функции![]() измеримо как пересечение двух измеримых
множеств. Таким образом,
измеримо как пересечение двух измеримых
множеств. Таким образом,![]() измерима.
измерима.
Теорема доказана.
Теорема 2.1.5.Пусть функция![]() задана на объединении не более чем
счетного числа измеримых множеств и
имеет измеримое сужение на каждое из
этих множеств. Тогда
задана на объединении не более чем
счетного числа измеримых множеств и
имеет измеримое сужение на каждое из
этих множеств. Тогда![]() является измеримой на объединении
множеств.
является измеримой на объединении
множеств.
Определение 2.1.2. Две функции![]() и
и![]() заданные на одном и том же множестве
называютсяэквивалентными, если
мера множества, на котором
заданные на одном и том же множестве
называютсяэквивалентными, если
мера множества, на котором![]() и
и![]() не равны, равна нулю, т.е.
не равны, равна нулю, т.е.
![]() .
.
При этом говорят, что функции
![]() и
и![]() равны почти всюду.
равны почти всюду.
Теорема 2.1.6.Если![]() измерима и функция
измерима и функция![]() эквивалентна
эквивалентна![]() ,
то функция
,
то функция![]() измерима.
измерима.
Доказательство.Множество![]() представим в виде
представим в виде и обозначим
и обозначим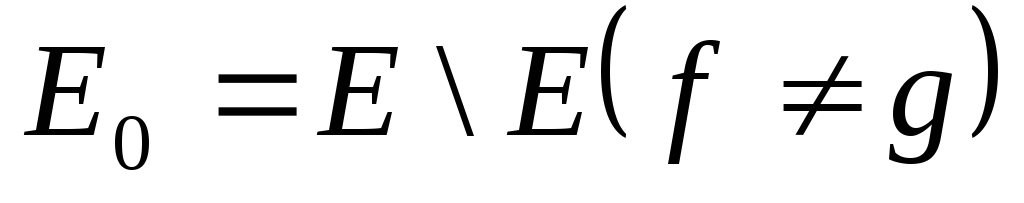 .
Сужение
.
Сужение![]() является измеримой функцией. Сужение
функции
является измеримой функцией. Сужение
функции![]() совпадает с сужением
совпадает с сужением![]() ,
и потому измеримо. Так как
,
и потому измеримо. Так как![]() ,
то
,
то![]() измеримая функция. В итоге функция
измеримая функция. В итоге функция![]() определена на объединении двух измеримых
множеств и измерима на каждом из них.
Применение теоремы 2.1.5 завершает
доказательство.
определена на объединении двух измеримых
множеств и измерима на каждом из них.
Применение теоремы 2.1.5 завершает
доказательство.
Теорема доказана.
Теорема 2.1.7. Функция непрерывная
на отрезке![]() измерима.
измерима.
Доказательство.Множество![]() измеримо. Для непрерывной функции
прообразом любого замкнутого множества
является замкнутое множество. Поэтому
Лебеговы множества
измеримо. Для непрерывной функции
прообразом любого замкнутого множества
является замкнутое множество. Поэтому
Лебеговы множества![]() измеримы для любого
измеримы для любого![]() .
.
Теорема доказана.
Следствие 2.1.1.Всякая кусочно-непрерывная на отрезке функция измерима.
Следующая теорема утверждает, что
множество всех измеримых функций,
определенных на измеримом множестве
![]() ,
замкнуто относительно операций сложения
и умножения на скалярный множитель.
,
замкнуто относительно операций сложения
и умножения на скалярный множитель.
Теорема 2.1.8.Пусть функции![]() и
и![]() измеримы и
измеримы и![]() - произвольный скаляр, тогда
- произвольный скаляр, тогда![]() и
и![]() измеримы на множестве
измеримы на множестве![]() .
.
Доказательство.Если![]() ,
то
,
то Иными словами, Лебеговы множества
Иными словами, Лебеговы множества![]() измеримы при любом
измеримы при любом![]() .
.
Для ненулевого
![]() ,
имеем
,
имеем
В силу измеримости функции
![]() оба множества измеримы. Таким образом,
любая функция вида
оба множества измеримы. Таким образом,
любая функция вида![]() измерима вместе с функцией
измерима вместе с функцией![]() .
.
Для доказательства второго утверждения покажем справедливость равенства
![]() ,
,
где
![]() - множество рациональных чисел.
- множество рациональных чисел.
Пусть
![]() ,
тогда
,
тогда![]() .
В силу всюду плотности множества
рациональных чисел на прямой, найдется
такое рациональное число
.
В силу всюду плотности множества
рациональных чисел на прямой, найдется
такое рациональное число![]() ,
что
,
что![]() .
Тогда
.
Тогда![]() и
и![]() .
Иными словами,
.
Иными словами,![]() и
и![]() .
Тогда
.
Тогда![]() .
Включение
.
Включение![]() показано.
показано.
Пусть
![]() ,
тогда найдется такое рациональное число
,
тогда найдется такое рациональное число![]() ,
что
,
что![]() .
Отсюда
.
Отсюда![]() и
и![]() .
Следовательно
.
Следовательно![]() и
и![]() ,
тогда
,
тогда![]() .
Иными словами,
.
Иными словами,![]() .
Обратное включение показано.
.
Обратное включение показано.
Применение теоремы 2.1.5 завершает доказательство.
Теорема доказана.
Теорема 2.1.9.Если функция![]() измерима, то измеримы функции
измерима, то измеримы функции![]() ,
,![]() и
и![]() ,
если функция
,
если функция![]() не обращается в нуль на множестве
не обращается в нуль на множестве![]() .
.
