М-Чм-зао-09

Контрольная работа №2

Тема. Итерационные методы решения систем линейных алгебраических уравнений

За д а н и е

1.Решить СЛАУ методами Якоби и Гаусса-Зейделя с заданной

точностью: ε=0,01. Проанализировать результаты решения (в зависимости от других значений ε.)

2. Сравнить результаты решения, полученные двумя методами, сделать соответствующие выводы.

Для расчета использовать СЛАУ AX=B, заданную в соответствием с вариантом из приложения 2.

Указания к выполнению второй работы Порядок выполнения работы

1.Решить заданную СЛАУ с использованием надстройки Поиск

решения.

2.Методом Якоби решить исходную СЛАУ. Сделать вывод о сходимости или расходимости итерационного процесса. Проиллюстрировать

это на графиках изменения каждой компоненты решения в зависимости от номера итерации (по аналогии с рис.2.3). Провести анализ условий сходимости итерационного процесса.

3.Преобразовать исходную систему к виду, пригодному для построения итерационного процесса, т.е. к системе с «преобладанием диагональных элементов» матрицы системы.

4.Вычислить вручную три итерации обоими методами, взяв в качестве начального приближения нулевой вектор. Выяснить вопрос о

продолжении или прекращении счета для ε=0,1

5.	_ _	_
	Привести полученную систему к нормальному виду X = β+ α X .
6.	Решить систему методами Якоби и Гаусса-Зейделя, используя
приложение Excel (на разных листах книги).
7.	Проследить сходимость итерационного процесса, построив графики

изменения каждой компоненты решения в зависимости от номера итерации (см.

рис.2.3).

2.1.Теоретические сведения 2.1.1. Метод Якоби (метод простых итераций)

Задана система линейных алгебраических уравнений

a11x1 + a12 x2 +.........	+a1n x n = b1
a21x1 + a22 x2 +.........	+a2n x n = b2 .	(2.1)
..........................................
an1x1 + an2 x2 +.........	+ann x n = bn

Или в матричной форме

11

_ _	(2.2)
A ´ X = B

Предполагаем, что диагональные элементы матрицы А отличны от нуля. Преобразуем систему (2.1-2.2) к эквивалентной ей, выражая неизвестное

xi из i-ого уравнения:

	x1 = (b1 − a12 x2 − .........	− a1n xn ) / a11
	x2 = (b2 - a21x1 -.........	- a2n xn ) / a22	(2.3)
	...................................................
	xn = (bn - an1x1 - .........	- an,n−1xn−1) / ann

Система (2.3) называется системой, приведенной к нормальному виду.

Вводя обозначения:

αij = -aij / aii ,

βi = bi

/ aii ,

i = 1,2,...n, j = 1,2,..n,

i ¹ j,

систему (2.3) можно записать в матричной форме:

_

_

_

(2.4)

гд

X = β+ α X

é 0 α

L α

_

β

éx

1n

ù

é

ù

ù

ê

12

ú

ê

1

ú

ê 1

ú

α =

êα21

0 L α2n ú

−

ê

β2 ú −

êx2

ú

(2.5)

ê

.

. .

ú,

β =

ê

ú, X =

ê

ú

ê .

ú

êKú

êLú

ëαn1

αn2

L 0

û

ë

βn û

ëxn û

Систему (2.4) решаем методом последовательных приближений (итераций). За нулевое приближение (нулевую итерацию) принимаем столбец

_	_	x1(0) = β1,		x2(0) = β2,.., xn(0) = βn
свободных членов X (0)	= β т.е.
Используя выражение (2.4), строим последовательность приближений
(итераций):		_
			_
	X (0)		= β
	_	(1)	_	_
	X		= β +α X (0)
	LLLLLL			(2.6)
		_	_	_
			_
	X (k ) = β +α X (k −1)

KKKKKK

Таким образом, получили последовательность приближений:

X (0) , X (1) ,...., X (k ) ,....

Если эта последовательность имеет предел	_	_	(k)
	X = lim X		, то он является
		k →∞

точным решением системы (2.1). На практике итерационный процесс продолжается до тех пор, пока два соседних приближения не станут достаточно близкими.

Критерий близости двух приближений может быть определен следующим образом:

M (k ) = max		xi( k ) - xi( k +1)		£ ε	(2.7)
i

12

Если условие (2.7) выполнено, то итерационный процесс прекращается и за приближенное решение системы (2.1) с заданной точностью ε принимается k-ое приближение, т.е.

_ _ (k )

X ≈ X .

2.1.2. Метод Гаусса-Зейделя

Метод Гаусса-Зейделя представляет собой модификацию метода Якоби. Основная идея метода заключается в том, что при вычислении (k+1)-ой итерации неизвестное xi(k +1) вычисляется с учетом уже найденных значений

x1(k +1) , x2(k +1) ,Kxi(−k1+1) .

Проиллюстрируем метод для n=3. Пусть система линейных алгебраических уравнений уже приведена к нормальному виду:

x1 = β1 + α12 x2 + α13x3							(2.8)
x2	= β2 + α21x1 + α 23x3
x3	= β3 + α 31x1 + α32 x2
						_	{x1(0) x2(0) x3(0)} и
Выбираем произвольное		начальное				приближение X (0)
подставляем в первое уравнение системы (2.8)
x (1) = β + α x (0)				+ α x		(0)
1	1	12	2	13	3

Полученное первое приближение x1(1) подставляем во второе уравнение системы (2.8)

x2(1) = β2 + α21x1(1) + α23 x3(0)

Используя x1(1) , x2(1) , находим x3(1) из третьего уравнения

x3(1) = β3 + α31x1(1) + α32 x2(1)

Этим заканчивается построение первой итерации

	(1) {x(1)	x(1)	x(1)	}	(2.9)
X
	1	2	3

Используя значения первого приближения X (1) можно таким же способом построить следующие итерации. Итерацию с номером (k+1) можно

представить следующим образом

x (k +1)	= β + α		12	x (k ) + α		13	x (k )
1	1			2			3
x2(k +1)	= β2	+ α21x1(k +1)			+ α23x3(k )			(2.10)
x3(k +1)	= β3	+ α31x1(k +1)			+ α32x2(k +1)

Итерационный			процесс продолжается до тех пор,	пока два соседних
приближения	_ (k )	_	(k +1)	Критерий близости
	X	, X	не станут достаточно близкими.

может быть задан так же, как и в методе Якоби:

13

2.1.3. Условия сходимости итерационного процесса.

Прежде чем применять итерационные методы для решения какой-либо системы, необходимо убедиться, что решение может быть получено, т.е. итерационный процесс сходится к точному решению.

Доказывается теорема, что, если хотя бы одна из норм матрицы нормальной системы (2.3-2.4) меньше единицы, то итерационный процесс сходится к единственному решению. Т.е. изложенные выше итерационные методы можно использовать для систем, удовлетворяющих одному из следующих условий:

α

n

αij

1

= max å

<1

i

j=1

α

n

αij

(2.11)

2

= max å

<1

j

i=1

α

3

=

å

αij

2 <1

i, j

Или, для системы (2.1-2.2) итерационный процесс сходится, если

элементы матрицы А удовлетворяют условию

aii

>> å

aij

,(i = 1,2,...,n)

(2.12)

i¹ j

т.е. модули диагональных элементов каждой строки больше суммы модулей всех остальных элементов. Это условие еще называют условием преобладания диагональных элементов.

2.2.Решение СЛАУ с использованием приложения Microsoft Excel

2.2.1Метод Якоби (метод простых итераций)

Пример 2.1. Найти решение системы линейных алгебраических уравнений методом Якоби.

8x1 + x2 - 4x3	= 6 ü
2x1 - 6x2 + x3		ï	(2.13)
	= -9ý
-x1 + x2 + 4x3 = 5		ï
		þ

Прежде всего, убеждаемся, что изложенные выше итерационные методы можно использовать для заданной системы, т.к. выполняется условие

«преобладания диагональных коэффициентов» (2.12), что обеспечивает сходимость этих методов.

Приведем эту систему к нормальному виду:

x1	= 0,75- 0,125x2 + 0,5x3		ü
x2	= 1,5+ 0,333x1	+ 0,167x3	ýï,	(2.14)
x3	= 1,25+ 0,25x1	- 0,25x2	ï
			þ

или в матричной форме

X = β +α X ,

где

14

é	0	- 0,125	0,5	ù		é0,75ù
α = ê0,333		0	0,167ú		× ,		= ê	1,5	ú	×
						β
ê				ú		ê			ú
ê	0,25	- 0,25	0	ú		ê			ú
ë				û		ë1,25			û

Не составит труда проверка сходимости итерационного процесса по формулам (2.11-2.12).

Последовательность действий:

1. Возьмем чистый лист Excel, назовем его Якоби. Заготовим таблицу, как показано на рис.2.1.

Рис.2.1.

2. Исходные данные, матрицы α и β , введем в ячейки В6:Е8. Значение

ε - в ячейку Н5. Номер итерации n сформируем в столбце А с помощью автозаполнения. В качестве нулевого приближения выберем нулевой вектор и введем его в ячейки В11:D11.

3. В ячейках В12:D12 запишем формулы для вычисления первого приближения, используя выражение (2.4). Эти формулы имеют вид:

B12=$E$6 + B11*$B$6 + C11*$C$6 + D11*$D$6,

C12=$E$7 + B11*$B$7 + C11*$C$7 + D11*$D$7,

D12=$E$8 + B11*$B$8 + C11*$C$8 + D11*$D$8.

Эти формулы можно записать иначе, используя функцию Excel СУММПРОИЗВ (см. пример 1.2)

4.В ячейку Е12 введем формулу: E12=ABS(B11-B12) и скопируем ее вправо, в ячейки F12:G12.

5.В ячейку Н12 введем формулу для вычисления M(k). Для этого используем выражение (2.7), т.е. Н10= (E12:G12). Функция МАКС находится в

категории статистические.

6.Выделим ячейки В12:Н12 и скопируем их вниз до конца таблицы. Таким образом, получим k приближений решения СЛАУ.

15

7. Определим количество итераций, необходимое для достижения заданной точности ε и приближенное решение системы. Для этого оценим степень близости двух соседних итерации по формуле (2.7). В ячейках столбца Н установим Условный формат. Для этого выделим ячейки Н12:Н20 и

выполним команду меню Формат\Условное форматирование и в открывшимся окне сделаем установки, как показано на рис.2.2. Щелкнув по кнопке Формат, установим цвет заливки.

Рис.2.2.

8. Результат такого форматирования виден на рис.2.1. Ячейки столбца Н, значения которых удовлетворяют условию (2.7) тонированы.

Анализируя результаты, принимаем за приближенное решение исходной системы с заданной точностью ε=0,1 четвертую итерацию, т.е.

_

X ≈ (1,022; 2,022; 0,991)

9. Исследуем характер итерационного процесса. Для этого выделим блок ячеек А10:D20 и построим графики, отражающие сходимость итерационного процесса, используя Мастер диаграмм. Приведенные графики подтверждают сделанный ранее вывод о сходимости итерационного процесса.

		Характер итерационного процесса
	3,0000
итерации	2,0000				x1
					x2
Значение
	1,0000				x3
	0,0000
	0	2	4	6	8
			Номер итерации

Рис.2.3.

Изменяя значение ε в ячейке Н5, получим новое приближенное решение исходной системы с новой точностью.

2.2.2. Метод Гаусса-Зейделя.

Пример2.2. Найти решение системы линейных алгебраических уравнений (2.13) методом Гаусса-Зейделя.

Последовательность действий:

1. Заготовим таблицу на новом листе Excel как показано на рис.2.4.

16

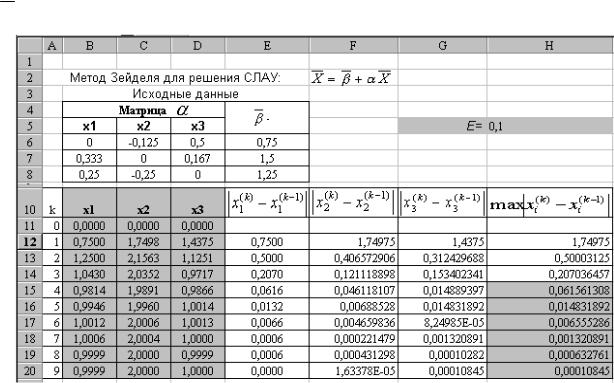
2. В качестве нулевого приближения выберем нулевой вектор X (0) = (0, 0, 0) и введем его в ячейки В11:D11.

Рис.2.4.

3.В ячейках В12:D12 запишем формулы для вычисления первого приближения, используя (2.9). Эти формулы имеют вид:

B12=$E$6 + B11*$B$6 + C11*$C$6 + D11*$D$6, C12==$E$7 + B12*$B$7 + C11*$C$7 + D11*$D$7, D12==$E$8 + B12*$B$8 + C12*$C$8 + D11*$D$8.

4.В столбце Н сформируем вычисление M(k) , используя выражение (2.10), так, как это проделали в предыдущем примере

5.Установим «условный формат» в ячейках Н12-H20, это наглядно покажет количество итераций, необходимое для достижения заданной степени

точности ε и приближенное решение системы.

_

Анализируя результаты, принимаем X ≈ {0,981; 1,989; 0,978} за приближенное решение исходной системы с заданной точностью ε=0,1.

17

Контрольная работа №3

Тема. Численные методы решения линейных дифференциальных уравнений с краевыми условиями. Метод конечных разностей

З а д а н и е

Решить краевую задачу методом конечных разностей для двух разностных сеток с шагом h и с шагом h/2, проанализировать полученные результаты. Исходные данные приведены в приложении 3.

Указания к выполнению третьей работы. Порядок выполнения работы

1.Записать конечно разностную систему линейных алгебраических уравнений (СЛАУ) с шагом h на отрезке [a,b] вручную.

2.Сформировать конечно разностную СЛАУ для шага h на отрезке [a,b]

сиспользованием Excel (расчетная схема приведена на рис.3.3).

3.Полученную систему уравнений решить любым известным вам

методом.

4.Уменьшить шаг сетки в 2 раза и еще раз решить задачу. Результаты представить в графическом виде.

5.Сравнить полученные результаты. Сделать вывод о необходимости поиска следующего приближения или о прекращении счета.

3.1.Теоретические сведения

Метод конечных разностей является универсальным численным методом решения краевой задачи. Достоинство этого метода в том, что он

позволяет свести решение краевой задачи к решению системы линейных алгебраических уравнений.

Линейная краевая задача для дифференциального уравнения 2-го порядка ставится следующим образом: найти функцию y=y(x), которая внутри отрезка [a, b] удовлетворяет дифференциальному уравнению

y'' + p(x)y' + q(x)y = f (x) ,

(3.1)

а на концах отрезка - линейным краевым условиям:

	α y(a) + α y' (a) = A		(3.2)
	0	1

β0 y(b) + β1 y' (b) = B

где p(x), q(x), f(x)- непрерывные на [a,b] функции; α 0 ,α 1 , A, β 0 , β 1 , B - заданные числа, не равные нулю одновременно.

3.1.1.Последовательность действий.

1.Область изменения аргумента x [a, b] заменяем разностной сеткой (дискретной сеточной областью)

Ωn { x0=a, xi = xi-1 +h , i = 1, 2, ….n, h = (b-a)/n},	(3.3)
18

Точки разбиения xi называются узлами, h - шагом сетки. Введем обозначения

pi = p(xi ),		qi = q(xi ),			fi = f (xi )
y	= y(x ),	y'	= y' (x ),	y'' = y'' (x ), i = 0,1,...,n
i	i	i	i	i	i

2. Производные y', y" в узлах сетки заменяем конечно-разностными отношениями через значения искомой функции y=y(x) в узлах сетки Ωn

y' =

yi +1 − yi −1

,

y'' =

yi −1

− 2yi

+ yi+1

.

(3.4)

h2

i

2h

i

Для граничных

точек

x0

= a,

x n

= b,

чтобы

не

выходить за пределы

отрезка [a,b], полагаем:

y1 − y0

yn − yn−1

y0' =

,

yn'

=

.

(3.5)

h

h

3. Подставим конечно-разностные выражения (3.4), (3.5) в дифференциальное уравнение (3.1) и краевые условия (3.2). Получим конечно разностную систему из (n+1) линейных алгебраических уравнений с

неизвестными y0 , y1,..., yn :

α

0

y +α

y1 - y0

= A

0

1

h

yi −1 - 2yi + yi +1

+ p

i

yi+1 - yi −1

+ q

i

y

= f

, i = 1,2,..,n -1

h2

2h

i

i

β0 yn + β1 yn -hyn−1 = B

После соответствующих преобразований система (3.6) имеет вид

b0 y0 + c0 y1 = A

i = 1,2,..,n -1,

ai yi−1 + bi yi + ci yi+1

= fi ,

где

an yn−1 + bn yn = B

1

pi

2

1

pi

a

=

-

,

b = q -

, c =

+

,

i = 1,2,..,n -1

h2

h2

h2

i

2h

i i

i

2h

b = α0 h −α1 ,

c = α1

,

a

n

= -

β1

,

b =

β0h + β1

.

0

h

0

h

h

n

h

В матричной форме система (3.7) имеет вид

A ×

=

_

,

Y

D

где

éb0

c0

ù

é

A

ù

êa

b

c

ú

ê

f

1

ú

ê

1

1

1

ú

ê

ú

ê

a2

b2

c2

ú

,

_

ê

f2

ú

,

A = ê

ú

D = ê

ú

êK K

K

K

K

ú

ê

K

ú

ê

a

n −1

b

n

−1

c

n

−1

ú

ê f

n

−1

ú

ê

ú

ê

ú

ê

a

n

b

n

ú

ê

B

ú

ë

û

ë

û

_

Y

é y0 ù êê y1 úú

= êê y2 úú. , ê K ú êê yn −1 úú êë yn úû

(3.6)

(3.7)

(3.8)

(3.9)

(3.10)

Решая систему (3.7), получим приближенное решение краевой задачи (3.1-3.2) на разностной сетке Ωn представляющее собой сеточную функцию вида Y(y0 , y1 , …,yn-1, yn)

19

3.1.2. Сходимость разностных методов

На практике оценка погрешности решения, полученного разностными методами, затруднительна. Поэтому при решении инженерных задач для правильного выбора шага h используют метод половинного шага. Находят численное решение задачи на сетке Ωn с шагом h и на сетке Ω2n с шагом h/2. Если значения полученных решений (двух сеточных функций) в одинаковых узлах отличаются друг от друга не более чем на 5%, то полученную сеточную функцию на сетке Ω2n принимают за приближенное решение задачи. В противном случае шаг еще раз уменьшают в два раза и повторяют решение.

Такая вычислительная схема хорошо реализуется на ЭВМ

3.2. Решение краевой задачи с использованием электронных таблиц Microsoft Excel.

Пример 3.1. Методом конечных разностей найти решение краевой задачи на отрезке x [1, 2] с шагом h=0,2 и с шагом h=0,1. Сравнить

полученные результаты и сделать вывод о необходимости поиска следующего приближения или о прекращении счета.

x2 y'' − 4 x y' + 6 y = x	(3.17)
y(1)=1, y’ (2)=0,5.	(3.18)

3.2.1. Построение первой итерации Последовательность действий

1.Подготовим таблицу, как это показано на рис.3.1. Введем значения

исходных данных: a, b, α 0 ,α 1 , A, β 0 , β 1 , B, n. Первоначальное количество разбивок возьмем n=5.

2.Вычислим шаг разностной сетки h=(b-a)/n в ячейке В5.

3.Номер узла i введем с помощью автозаполнения в столбец А

таблицы.

4.Значения узлов разностной сетки определим по формуле xi =a+h*i, i=0,1, ,n. Для этого в ячейку В8 введем формулу: =$B$3+$B$5*A8 и скопируем

еевниз до конца таблицы (до х=2).

5. В столбцах C, D таблицы вычислим значения функций

	p(x) =	− 4	,	q(x) =	6	,	в узлах сетки xi, i=1,2,.n-1 (для i=1,2,3,4).
		x			x2

После этого приступим к формированию разностной СЛАУ (3.7).

6.В столбцах Е, F, G таблицы вычислим значения коэффициентов аi вi , сi по формулам (3.8-3.9), как это показано на рис.3.1.

7.В столбце Н таблицы сформируем вектор правой части СЛАУ,

вектор D , используя выражение (3.10)

20