М-Чм-зао-09

Пермский государственный технический университет Строительный факультет

Кафедра строительной механики и вычислительной техники

Методические указания для самостоятельной работы и контрольные задания по дисциплине

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ

для студентов заочников специальностей ПГС-290300, ВВ-290800

ПСК-290600, ТВ-290700

Пермь 2009

План УМД 2009\2010 уч.г.

Методические указания для самостоятельной работы и контрольные задания по дисциплине

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ

Составитель: Кашеварова Г.Г., к.т.н., доцент, Пермякова Т.Б., к.т.н., доцент.

Приведены методические указания по самостоятельному изучению дисциплины "Численные методы решения задач", задания и методические указания по выполнению контрольных работ. Предназначены для студентов заочного факультета.

Рецензент: С.Г.Кузнецова к.т.н., доцент

Издание стереотипное.

Утверждено на заседании кафедры СМиВТ от 8 октября 2009 г.

2

Введение

Студенты, обучающиеся на строительном факультете специальности ПГС-290300, ВВ-290800 ПСК-290600, ТВ-290700 заочного отделения изучают дисциплину "Численные методы решения задач ".

Распределение объемов занятий и видов учебной работы дано в табл.1.

Таблица 1.

Семе		Занятия, ч.			Контроль
стр	Лекции	Практиче	Самостоятель
		ские		ная работа
5	6	6		118	Зачет

Основной формой изучения дисциплины является самостоятельная работа студента над рекомендованной литературой. Целесообразно прорабатывать материал, пользуясь приведенным ниже списком вопросов и краткими пояснениями к ним.

Список литературы Основная

1.Кашеварова Г.Г., Пермякова Т.Б. Численные методы решения задач строительства на ЭВМ. Пермь. 2003.-351с.

2.Турчак Л.И. Основы численных методов. М.: Наука 1987.-342с.

3.Волков Е.А. Численные методы. -М. Наука. 1987. –248 с.

Литература дополнительная

4.А.А.Самарский, А.В.Гулин. исленные методы. М. Наука. 1989. -430с.

5.Б.П.Демидович, И.А.Марон. Численные методы анализа. М. "Наука". 1967.-368с.

6.С.И. Зуховицкий. Линейное и выпуклое программирование. . М. "Наука". 1964.-348с.

7.Попов А. Excel. Практическое руководство. М.: ДЕСС КОМ. 2000. -354

с.????????

Краткие методические указания по самостоятельному изучению курса

Методические указания содержат формулировку вопроса, номер

соответствующего раздела в рекомендованной литературе и сжатый комментарий.

1.Численные методы решения задач линейной алгебры [1, глава 1].

ØПрямые (точные) методы решения систем линейных алгебраических уравнений. Метод Гаусса.

ØВычисление определителя и обратной матрицы методом Гаусса.

ØОбусловленность матриц. Плохо обусловленные системы линейных алгебраических уравнений.

ØИтерационные методы решения систем линейных алгебраических уравнений. Метод Якоби и Гаусса-Зейделя. Условия сходимости итерационного процесса.

ØСпециальные типы матриц, возникающие в практических задачах.

3

2.Численные методы решения обыкновенных дифференциальных уравнений [1, глава 6, п.п.6.1, 6.4, .6.6].

ØЗадачи Коши и краевые задачи в расчетах строительных конструкций. Необходимость решения их численными методами.

ØРазностная схема решения краевой задачи для линейного дифференциального уравнения 2-го порядка.

3.Численные методы оптимизации [1, глава 8, п.п.8.1, 8.3,8.5].

ØМатематические задачи оптимизации в строительстве.

ØЗадача линейного программирования. Геометрическая интерпретация задачи линейного программирования. Симплекс-метод решения задач линейного программирования.

Задания на контрольные работы и методические указания к их выполнению

Контрольную работу каждый студент выполняет в соответствии с индивидуальным вариантом. Номер варианта определяет преподаватель. Варианты заданий приведены в приложениях.

Работа выполняется с использованием электронных таблиц Microsoft Excel. Рабочие лист Excel должны содержать все расчеты, необходимые для решения поставленной задачи и соответствующие выводы. Выводы можно сделать вручную непосредственно на распечатке рабочего листа. Распечатка должна содержать: фамилию, имя, код группы, краткую постановку задачи, номер варианта.

Контрольные работы должны быть представлены на бумажном (распечатка) и электронном (дискета) носителях.

Работы, выполненные полностью или частично, не по заданному варианту не рецензируются.

Защита контрольных работ происходит по расписанию в дисплейном классе с обязательной демонстрацией проведенных расчетов в Excel. Для успешной защиты необходимо:

Øуметь объяснить ход выполнения расчетов, правильность использования расчетных формул и графических построений, понимать смысл входящих в них величин;

Øуметь объяснить полученные результаты;

Øзнать идеи используемых численных методов в пределах программы курса.

4

Контрольная работа №1

Тема. Численные методы решения задач линейной алгебры,

метод Гаусса

За д а н и е

1.Решить систему линейных алгебраических уравнений (СЛАУ) AX =B,

вычислить определитель и обратную матрицу для матрицы А методом исключения Гаусса.

2.Сделать выводы о корректности задачи (существование, единственность, устойчивость решения относительно исходных данных).

Указания к выполнению первой работы Порядок выполнения работы

1.Для расчета использовать матрицу А, заданную в соответствии с вариантом из приложения 1. Вектор свободных членов B задать произвольно.

2.Решить полученную вами СЛАУ AX =B методом Гаусса:

Øпрямой ход: привести СЛАУ к эквивалентной системе с

треугольной матрицей системы, т.е. A X = B

Øобратный ход: последовательно вычислить неизвестные х1,х2,…,хn

3.Проверить полученное решение СЛАУ, используя надстройку Excel

поиск решения применительно к исходной системе AX = B .

4.Вычислить вручную методом Гаусса определитель матрицы А, матрицу А-1, обратную матрице A,. Проверить сделанные расчеты на ЭВМ, используя матричные функции Excel.

5.Вычислить нормы матриц А и А-1 (вручную).

6.Исследовать обусловленность матрицы, вычислив меру

обусловленности ν(А). Сделать заключение об обусловленности матрицы A и заданной системы.

7.Задать небольшое возмущение исходных данных (~0.1) и снова решить систему, используя надстройку поиск решения. Проанализировать, как изменились результаты, оценив относительную погрешность решения (%).

8.Проанализировав полученные данные, сделать заключение о корректности исходной задачи.

1.1. Теоретические сведения

1.Система линейных алгебраических уравнений в общем случае имеет

вид:

a11x1 + a12 x2 +.........	+a1n x n = b1
a21x1 + a22 x2 +.........	+a2n x n = b2	,	(1.1)
..........................................
an1x1 + an2 x2 +.........	+ann x n = bn
	5

В некоторых случаях эту систему удобнее записывать в матричной

форме:

_ _	(1.2)
A ´ X = B ,
_	_

где А - матрица системы, X - вектор решения, B - вектор свободных членов.

éa

a

K a

1n

ù

éx

ù

éb

ù

ê

11

12

ú

ê 1

ú

ê 1

ú

A =

êa21

a22

K a2n ú

_

êx2 ú

_

êb2 ú

êK K K K ú

; X =

êKú

; B =

.

êKú

ê

an2

ú

ê

ú

ê

ú

ëan1

K ann û

ëxn

û

ëbn

û

2.Система (1.1−1.2) имеет единственное решение, если матрица А является невырожденной (detA¹0).

3.Матрицы А и В являются исходными данными и во многих случаях задаются приближенно. Встает вопрос, как погрешности исходных данных влияют на точность решения.

Говорят, задача плохо обусловлена, если она чувствительна к малым изменениям входящих в нее исходных данных. В противном случае – хорошо обусловлена.

Обусловленность является качественной характеристикой, хотя мы будем стараться оценить ее и количественно, используя величину меры

обусловленности

ν ( A) =				A				*	A−1	.	(1.3)

4.Матрица А-1 называется обратной по отношению к данной матрице А

инаходится из условия

А А-1= А-1 А =Е.

(1.4)

Процесс нахождения обратной матрицы называется обращением матрицы. Доказывается теорема, что если определитель матрицы А отличен от нуля ( det A ¹ 0), то она имеет обратную матрицу А-1.

5. Величина А называется нормой матрицы A = [aij ]и определяется по одной из 3-х формул:

	A				1	= max å|aij				|;
							i	j
	A				1	= max å|aij				|;	(1.5)
							j	i
	A				3	=	å|aij		|2 .
							i , j
6.Система (1.1-1.2) является хорошо обусловленной, а ее решение –
устойчивым, если мера обусловленности ν ( A)											близка единице.

7. Задача решения СЛАУ является корректной, если решение существует и единственно (detA¹0) и устойчиво относительно исходных данных (А и В), т.е. малым изменениям исходных данных соответствуют малые изменения решения задачи.

6

8. Метод Гаусса (метод последовательного исключения). Суть метода

заключается в последовательном исключении неизвестных из системы уравнений. Процесс состоит из двух этапов: прямого и обратного ходов. В результате прямого хода система приводится к треугольному виду, а при выполнении обратного хода вычисляются все неизвестные.

Продемонстрируем метод Гаусса на примере системы из трех уравнений. Обозначим каждое уравнение буквами A(i) , B(i), C(i) (здесь (i) соответствует номеру шага).

a	x + a		x	+ a	x	= b ;	A(0)
11	1	12	2	13	3	1		(1.6)
a21x1		+ a22 x2 + a23x3				= b2 ;	B(0)
a	x	+ a	x	+ a	x	= b ;	C(0)
31	1	32	2	33	3	3

Прямой ход.

Шаг 1. Допустим, a11 отличен от нуля (ведущий элемент). Разделим 1-ое уравнение на a11 . Умножим последовательно коэффициенты полученного уравнения на (- a21 ) и (- a31 ) и суммируем с соответствующими элементами - 2- ой и 3-ей строк. Выполняемые действия показаны справа от системы уравнений. В результате выполнени этого шага из всех уравнений, кроме 1-го исключено неизвестное х1.

x + a(1) x			+ a(1) x		= b(1)	;		A(1)	= A(0) / a
1	12	2	13	3	1				11
	a(1) x + a(1) x			3	= b(1)	;		B(1)	= B(0) + A(1) * (−a	21	)
	22	2	23		2
	a(1) x + a(1) x			3	= b(1)	;		C(1)	= C(0) + A(1) (−a		)
	32	2	33		3					31

Шаг 2. Первое уравнение остается неизменным. Исключим неизвестное х2 из 2-го и 3-го уравнений. Выполняемые действия показаны справа от системы уравнений.

x + a(1) x			+ a(1) x		= b(1) ;		A(2) = A(1)
1	12	2	13	3	1
		x2	+ a23(2) x3		= b2(2) ;		B(2)	= B(1) / a22(1)	(1.7)
			a(2) x		= b(2)	;	C(2)	= C(1) + B(2) (−a	(1) )
			33	3	3			32

Выполнив 2 шага для системы 3-го порядка, получили систему (1.7), эквивалентную заданной. Матрица этой системы является треугольной и неизвестные системы вычисляются достаточно легко.

Обратный ход. Из последней строки полученной системы (1.7) находим

b(2)

значение 3-ей компоненты вектора-решения x3 = a3(2) . Подставляя его во вторую

33

строку системы, получим вторую компоненту вектора-решения x2 = b2(2) − a23(2) x3 . Имея x2 , x3 , аналогичным образом найдем x1 из первого уравнения системы (1.7)

x1 = b1(1) − a12(1) x2 − a13(1) x3 .

7

1.2. Решение задач линейной алгебры с использованием приложения

Microsoft Excel

1.2.1. Матричные функции Excel

Для решения задач линейной алгебры используются матричные функции Excel из категории математические:

МУМНОЖ(<матрица1>;<матрица2>) – возвращает произведение

матриц.

МОБР(<матрица>) – возвращает матрицу, обратную к данной. МОПРЕД(<матрица>) – вычисляет определитель исходной

квадратной матрицы.

Порядок обращения к матричным функциям:

Øвыделить блок, где будет размещен результат матричной операции;

Øв мастере функций выбрать нужную категорию и нужную функцию;

Øубрать окно соответствующей функции (с помощью кнопки ) или отбуксировать его в сторону от исходных данных;

Øвыделить исходную матрицу (бегущая пунктирная линия);

Øодновременно нажать клавиши Shift+Ctrl+Enter.

1.2.2. Реализация метода Гаусса средствами приложения Excel

Пример 1.1. Найти решение системы линейных алгебраических

уравнений

2x1	+ 4x2 + 3x3 = 4 ü
3x1	+ x2 - 2x3 = -2 ýï ,	(1.8)
4x1	ï
	+ 11x2 + 7x3 = 7þ

используя алгоритм метода Гаусса.

Последовательность действий:

Возьмем чистый лист Excel, назовем его Гаусс. Введем расширенную матрицу системы, как показано на рис.1.1 в ячейки А3:D5.

Первый этап, приведение матрицы системы к треугольной.

1.Поделим элементы первой строки на а11 .Для этого в ячейку А7 введем формулу А7=А3/A$3$ (*смотри сноску) и скопируем ее вправо до конца строки.

2.Умножим элементы первой строки на (-а21 ) и прибавим ко 2-ой строке. Для этого введем формулу А8=А7(-А$4$)+А4 и скопируем ее вправо до конца строки.

3.Умножим элементы первой строки на (-а31 ) и прибавим к 3-ей строке. Для этого введем формулу А9=А7(-А$5$)+А5 и скопируем ее вправо до

конца строки. Таким образом исключили неизвестное х1 из 2-го и 3-го уравнений системы (смотри 1-ый шаг рис.1.1).

*- данная запись означает, что в ячейку А7 вводится формула, начинающаяся со знака «=» (равно).

8

4. Осталось исключить неизвестное х2 из 3-го уравнения системы. Для этого реализуем описанный выше алгоритм для 2-ой и3-ей строк (смотри

2-ой шаг рис.1.1).

Рис.1.1.

На этом первый этап метода Гаусса, закончен, матрица системы приведена к треугольной.

Второй этап. Здесь последовательно найдем неизвестные, начиная с последней строки. Для этого в ячейки G12:G14 запишем формулы:

G4=D13/C13

(для вычисления x3);

G3=D12-C12*G4

(для вычисления x2);

G2=D11-C11*G4-B11*G3

(для вычисления x1).

1.2.3. Решение СЛАУ с помощью надстройки

Поиск решения

Пример 1.2: Найти решение СЛАУ из примера 1.1, используя надстройку

Поиск решения.

использует итерационные

При решении СЛАУ AX

=B приложение Excel

(приближенные) методы. Строится последовательность приближений

(i ) ,

X

i=0,1,…n. Назовем вектором невязок следующий вектор:

R ( i ) = A

( i ) −

X

B

(1.9)

(i) ,

Задача Excel заключается в том,

чтобы найти такое приближение

X

при котором вектор невязок был бы нулевым, т.е. добиться совпадения значений правых и левых частей системы AX=B.

9

Последовательность действий

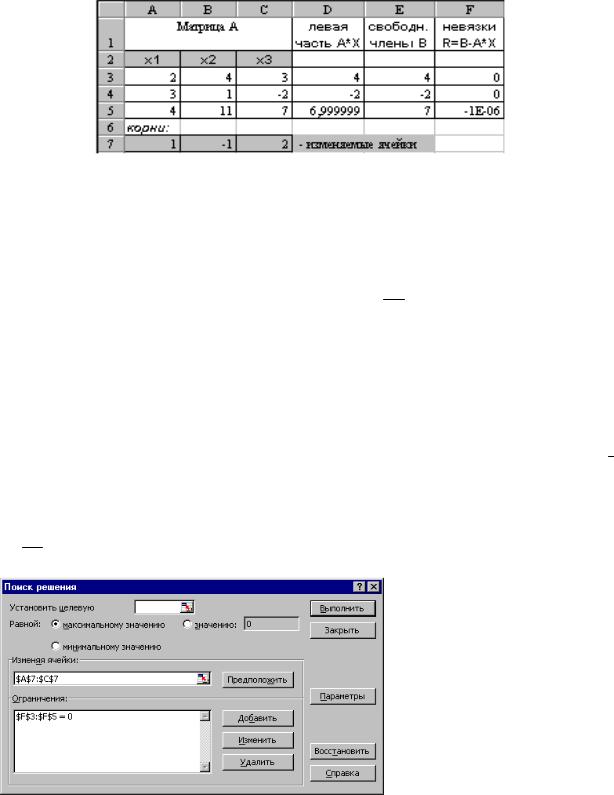
1. Возьмем новый лист (а можно и на том же). Заготовим таблицу, как показано на рис.1.2.

Рис.1.2.

2. Заготовим ячейки А7:С7, где будет сформировано решение системы (х1, х2, х3). Первоначально они остаются пустыми, т.е. равными нулю. Однако для контроля правильности вводимых далее формул, удобно ввести в эти ячейки какие-либо значения, например единицы. Эти значения можно рассматривать

как нулевое приближение решения системы, X ( 0 ) (1, 1 , 1) .

3.Введем коэффициенты системы (матрицу А) в ячейки А3:С5.

4.В столбец D введем выражения для вычисления левых частей исходной системы. Для этого в ячейке D3 введем и скопируем вниз до конца таблицы формулу: D3=СУММПРОИЗВ (A3:C3;$A$7:$C$7).

Используемая функция СУММПРОИЗВ принадлежит категории

Математические.

5.В столбец Е запишем значения правых частей системы (матрицу B).

6.В столбец F введем невязки в соответствии с формулой (1.9), т.е. введем формулу F3=D3-E3 и скопируем ее вниз до конца таблицы.

7. Будет не лишним проверить правильность вычислений для случая

X ( 0 ) (1, 1 , 1) .

8. Зададим команду меню Сервис\Поиск решения. В окне Поиск решения (рис.1.3) в поле

Изменяя ячейки укажем блок $А$7:$С$7, а в поле

Ограничения – $F$3:$F$5=0.

Для этого надо щелкнуть на кнопке Добавить и ввести эти ограничения.

9. Щелкнем на кнопке

Выполнить.

Рис. 1.3.

Полученное решение системы (1.8) х1=1; х2=-1 х3=2 записано в ячейках А7:С7, рис.1.2.

10