Блок 1.

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы.

Действия:

1) Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.

α × (А + В) = αА + αВ; α × (βА) = (αβ) × А;

2) Суммой матриц А и В, называется матрица С, элементы которой равны сумме соответствующих элементов. А + В = В + А; А + (В + С) = (А + В) + С; А + 0 = А; А - А = 0; 1 × А = А;

3) Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

Определитель I-го порядка – число ∆n , заданное с помощью таблицы [a₁₁; a₁₂; a_1n; a₂₁; a₂₂; a_2n] и вычисленное с помощью всех элементов таблицы.

aij  i – номер строки, j – номер столбца

1<j<n 1<j<m

Вычисление

1) n=1 , то

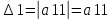
2) n=2 , то

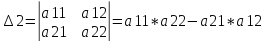
3) n=3 , то

Свойства определителей.

1) Если строки определителя взаимно заменить соответствующими столбцами, то определитель не изменится.

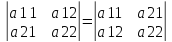
2) Если поменять местами любые 2 строки, то определитель поменяет знак.

3) Общий множитель любой строки можно вынести за знак определителя.

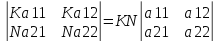
4) Если в определителе есть одна нулевая строка или столбец, то определитель равен нулю.

5) Если в определителе любые две строки равны, то определитель равен нулю.

6) Если в определителе 2 строки пропорциональны, то определитель равен нулю.

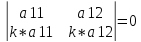
7) Если к элементам одной строки прибавить элементы другой строки, умноженные на некоторое число, отличное от неё, то определитель не изменится.

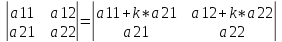
Системы линейных алгебраических уравнений.

1) Система двух линейных уравнений с двумя неизвестными.

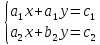
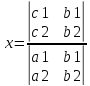
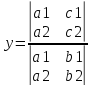
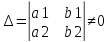
2) Система двух линейных уравнений с тремя неизвестными.

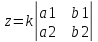k- произвольное число

3) Система трёх линейных уравнений с тремя неизвестными.

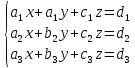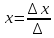
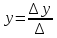
Единственное решение: 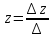(теорема Крамера),

где

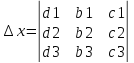
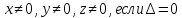
Блок 7.

Возрастание и убывание функций.

Если функция f(x), имеющая производную на отрезке [a;b], возрастает на этом отрезке, то её производная на отрезке [a;b] не отрицательна, т.е. .

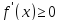Если функция f(x) непрерывна на отрезке [a;b] и дифференцируема в промежутке (a;b) , причём f’(x)>0 для a<x<b , то эта функция возрастает на отрезке [a;b].

Если f(x) убывает на отрезке [a;b], то f'(x)=<0 на этом отрезке. Если f'(x)<0 в промежутке (a;b), то f(x) убывает на отрезке [a;b].

Максимум и минимум функции.

max: функция f(x) в точке x1 имеет max, если значение f(x) в точке x больше, чем её значения во всех точках некоторого интервала, содержащего точку x1.

min: функция f(x) имеет min при x>x2, если 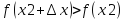при любых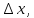достаточно малых по абсолютной величине.

Необходимое и достаточное условия экстремума.

Необходимое: если дифференцируемая функция y=f(x) имеет в точке x=x1 max или min , то её производная обращается в нуль в этой точке, т.е. .

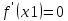Достаточное: пусть функция f(x) непрерывная в некотором интервале, содержащем критическую точку x1 , и дифференцируема во всех точках этого интервала. Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то при x=x1, функция имеет max. Если же при переходе через точку x1 слева направо производная меняет знак с минуса на плюс, то функция имеет в этой точке min.