1) Табличный способ

x	x1	x2	x3	xn
y	y1	y2	y3	yn

2) Графический способ.

3) Аналитический способ.

y=f(x) =>

Предел функции.

Число b называется пределом функции f(x) при x, стремящимся к a, если всегда из того, что x стремится к a, не принимая значения a, следует, что f(x) стремится к b.

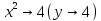
Замечания о пределах.

Существуют пределы слева и справа от точки.

b1 – левый предел ; b2 – правый предел.

!!!!!!!!!ГРАФИК!

Функция имеет предел тогда, когда левое предельное значение равно правому предельному значению.

Бесконечно малые и бесконечно большие функции.

Определение: для любого M существует

–бесконечно малая функция

- бесконечно большая функция

Основные правила вычисления пределов

1) Предел

2) Предел от суммы 2х функций равен сумме их пределов

3)Предел произведения – аналогично П.2

4) Предел частного – аналогично П.2

Первый и второй замечательные пределы

Натуральные логарифмы.

при

Непрерывность функций.

Функция непрерывна в

Условия непрерывности

1) 2)3)

4)

Если выполняется 2 условие, но не выполняетя 3, то это разрыв 1го рода.

Если f из пределов равен бесконечности, то это разрыв 2го рода.

Блок 6.

Производная функции.

- приращение. x – произвольная точка.

Производная y=f(x) в точке x называется предел отношения приращения функции к прирощению аргумента, при стремлении последнего к нулю.

Физический смысл производной.

Производная функции – это скорость изменения функции.

Дифференциал и его практическое применение.

(I – дифференциал функции)

Производные высших порядков.

Уравнение касательной в точке M на кривой

Уравнение нормали

Некоторые теоремы о дифференцируемых функциях.

Теорема Роля о корнях производной. Если функция f(x) непрерывна на отрезке [a;b], дифференцируема во всех внутренних точках этого отрезка и на концах x=a и x=b обращается в нуль [f(a)=f(t)=a], то существует внутри отрезка [a;b] по крайней мере одна точка x=c, a<c<b , в которой производная f'(x) обращается в нуль, т.е. f’(c)=0.

Теорема Лагранжа о конечных приращениях.

Если функция f(x) непрерывна на отрезке [a;b] и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка [a;b] найдётся по крайней мере одна точка c. a<c<b, что f(b)-f(f)=f’(c)(b-a).

Теорема Коши об отношении приращения двух функций.

Если f(x) и - дву функции, непрерывные на отрезке [a;b] и дифференцируемые внутри него, причём нигде внутри отрезка не обращается в нуль, то внутри отрезка [a;b] найдётся такая точка c , a<c<b , что

Раcкрытие неопределённостей вида 0/0 по правилу Лопиталя.

Пусть функции f(x) и на некотором отрезке [a;b] удовлетворяет условию теоремы Коши и обращается в нуль в точке x=a, т.е. 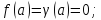тогда, если существует предел отношения

причём

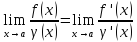
Раcкрытие неопределённостей вида по правилу Лопиталя.

Пусть функции f(x) и непрерывны и дифференцируемы при всехв окрестности точкиa, причём производная не обращается в нуль; пусть, далее,

Тогда существует предел и

Формула Тейлора.

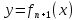
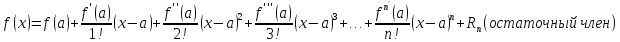
или

Примеры разложения функций по формуле Маклорена.