
shpory_traktora
.doc
|
2,4)
Рассмотрим процесс включения цепи
RC под синусоидальное напряжение Напряжение uCу в установившемся режиме
где
Если
конденсатор не был заряжен, то
Напряжение на конденсаторе будет равно
Ток в переходном режиме
Если конденсатор был предварительно заряжен, то
|
Из (9.27) и (9.28) видно, что переходный процесс зависит от величины Ψ.
Если
Если
включение происходит при Ψ = j, то
свободное напряжение Максимальное
значение напряжение |
3,1)
Апериодическим разрядом конденсатора,
заряженного до напряжения поля конденсатора, но и энергия, которая запаслась в магнитном поле катушки. 3,2) предельный случай апериодического разряда конденсатора имеет место, если сопротивление контура г равно критическому гкр, т. е. корни характеристического уравнения (13-34) вещественные и равные: Pi = ft = P = -r/2L. (13-42) Общее решение однородного дифференциального уравнения (13-33) дается в этом случае формулой uCcB = uc = (A1 + A2t)ePt. (13-43) На основании (13-32) для свободного тока tCB получим: iCB = i = С (А2 + рАг+ рА4) (13-44) -При начальных условиях ис (0) = U0 и i (0) = 0 находим постоянные интегрирования Ах = А2 — — pU0. Подставляя значения Лх и А2 в соотношения (13-43) и (13-44), получаем ток и напряжение на емкости: uc = U0(\-pt)e*\ (13-45) i = — CpZUoteP* = teP*. (13-46) Определим также напряжение на индуктивности: uL = L%=-U0(\+pt)ePt. (13-47) Кривые изменения i, ис и uL по форме не отличаются от приведенных на рис. 13-18ГОТ1 б. =
|
|
3,3) Периодический (колебательный) разряд конденсатора на цепь с резистором и катушкой
При
соотношении параметров контура из
конденсатора, катушки и резистора p1,2 = -α ± jω,
где
α = R / (2L) – коэффициент
затухания свободной составляющей;
Поскольку
Свободная составляющая переходного напряжения при комплексно-сопряженных корнях (см. п.п. 5.2.1)
uCсв Для свободной составляющей тока имеем iсв = C A e-αt (-α sin(ω0t + ψ) + ω0 cos(ω0t + ψ)). С учетом начальных условий при t = 0, uC = U0 , i = 0 из последних двух уравнений находим константы интегрирования: U0 = A sin ψ; 0 = C A (-α sin ψ + ω0 cos ψ). и далее
Запишем переходные напряжения и ток: uC = UCm e-αt sin(ω0t + ψ); i = -Im e-αt sin(ω0t + π); uL= ULm e-αt sin(ω0t - ψ),
|
зависимости переходных напряжения и тока uC, i показаны на рис. 5.15. Они представляют собой затухающие синусоиды. Скорость затухания колебаний оценивают декрементом колебаний. Декремент колебания - это постоянная, зависящая от параметров R, L, С и равная отношению амплитуд переходных параметров, отстающих друг от друга на период колебания Т0, например:
|
3,4) Включение RLC-цепи на постоянное напряжение
Рассмотрим
процесс при нулевых начальных условиях,
т.е. Уравнение цепи запишется в виде
Его решение
Ток установившегося режима равен нулю, поэтому
Начальные условия: i(0) = 0 = A1 + A2.
Учитывая,
что
|
|
4,2) Этапы расчета переходного процесса в цепи классическим методом:
|
Применительно к электрическим цепям в качестве частного решения неоднородного дифференциального уравнения выбирают установившийся режим в рассматриваемой цепи (если он существует), т. е. постоянные токи и напряжения, если в цепи действуют источники постоянных ЭДС и токов, или синусоидальные напряжения и токи при действии источников синусоидальных ЭДС и токов. Токи и напряжения установившегося режима называютустановившимися. Общее решение однородного дифференциального уравнения описывает процесс в цепи без источников ЭДС и тока, который поэтому называютсвободным процессом. Токи и напряжения свободного процесса называют свободными, а их выражения должны содержать постоянные интегрирования, число которых равно порядку однородного уравнения. РАЗДЕЛ №3 1,1) Cущность операторного метода Сущность операторного метода: функции действительной переменной времени f(t) ставится в соответствие по определенному правилу функция комплексной переменной F(S) такая, что дифференциальные уравнения функции действительной переменной превращаются в алгебраические уравнения функции комплексной переменнойf(t) ÷>F(S). Функцией действительной переменной в этом случае называется оригинал, а функция комплексной переменной - изображением.
|
1,2) Преобразование Лапласа представляет собой математический метод решения линейных дифференциальных уравнений. Преобразование Лапласа позволяет свести дифференциальное уравнение к алгебраическому уравнению. Как известно, линейные цепи, и фильтры в первую очередь описываются дифференциальными уравнениями, поэтому преобразование Лапласа позволяет легко проектировать частотно-избирательные фильтры. Применение преобразования Лапласа можно свести к следующему алгоритму:
Преобразование Лапласа непрерывной функции времени f(t), которая определена только для положительного времени (t > 0) математически выражается как:
где s(t) — комплексное число s = σ + jω
|
||||
|
1,3)
Линейность преобразования Лапласа. Так
как формула прямого преобразования
линейна относительно подынтегрального
сомножителя f(t),
то преобразование линейно —
изображение суммы оригиналов
a) Непосредственное применение интеграла прямого преобразования дает
Полученный
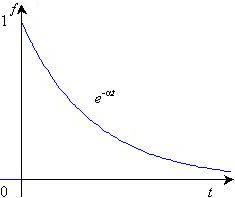
результат приводит к изображению единичной
функции f(t) = 1(t)
(рис. 19.2, б).
Найдем его, принимая в формулах для
экспоненты = 0.
Таким образом, 1(t)
имеет изображение 1/s.
По основной формуле преобразования
изображение –функции
|
1,5) Формула разложения.
Переход
от изображения
которую называют формулой разложения.
Левая
часть формулы является функцией 2,1) Закон Ома для k-й ветви
Следует отметить, что структура записи операторного сопротивления ветви и комплексное сопротивление той же ветви тождественны. Одно из другого можно получить заменой p на jω, т.е. Zk(p) ® Zk(jω). 2,2) Законы Кирхгофа в операторной форме Первый закон Кирхгофа: алгебраическая сумма изображений токов, сходящихся в узле, равна нулю
Второй закон Кирхгофа:алгебраическая сумма изображений ЭДС, действующих в контуре, равна алгебраической сумме изображений напряжений на пассивных элементах этого контура
2,3)
|
РАЗДЕЛ 4 1,1) 1,2) При разложении в ряд Фурье функция представляется следующим образом:
Здесь
В
выражении (1)
|
||||
|
1,3) Действующие значения несинусоидального тока и несинусоидального напряжения.
По
определению (см. § 3.2), квадрат
действующего значения тока
Если
то
Но Поэтому
или
Так
как амплитуда гармоники тока Следовательно, действующее значение несинусоидального тока равно корню квадратному из суммы квадратов постоянной составляющей тока и действующих значений отдельных гармоник. От углов сдвига фаз действующее значение тока не зависит. Аналогично, действующее значение несинусоидального напряжения U равно корню квадратному из суммы квадратов постоянной составляющей и действующих значений отдельных гармоник:
|
1,4) Коэффициент формы определяется как отношение действующего значения тока или напряжения к его среднему по модулю значению, т.е.
Для синусоиды Кф= 1,11.
1,5)
Коэффициенты,
характеризующие форму несинусоидальных
периодических кривых
При
оценке несинусоидальных периодических
кривых в электроэнергетике, где
кривые преимущественно симметричны
относительно оси абсцисс, пользуются
коэффициентом формы кривой
|
|
|
2,1) Мощность периодических несинусоидальных токов Активная мощность периодического тока произвольной формы определяется как средняя мощность за период
Если мгновенные значения напряжения и тока выразить в виде тригонометрических рядов, то получим:
Так
как среднее за период значение
произведения мгновенных значений
синусоид различной частоты равно
нулю (см. § 12-3) и тригонометрические
ряды абсолютно сходятся при любых
частотах
или после интегрирования
где
Из
этого выражения следует очень важный
вывод, что средняя мощность
несинусоидального тот равна сумме
средних мощностей отдельных гармоник
(постоянная составляющая рассматривается
как нулевая гармоника с
Полученная таким образом мощность представляет собой активную мощность или энергию, необратимо преобразуемую в единицу времени в данном участке цепи в тепловую, механическую или какую-либо иную форму энергии.
|
2,2)
расчет
цепей с несинусоидальными периодическими
ЭДС, напряжениями и токами
Если
в линейной цепи действует один или
несколько источников несинусоидальных
периодических ЭДС и токов, то расчет
такой цепи распадается на три этапа:
1.
Разложение ЭДС и токов источников
на постоянную и синусоидальные
составляющие (получение дискретного
спектра).
2.
Применение принципа наложения и
расчет токов и напряжений в цепи для
каждой из составляющих в отдельности.
3.
Совместное рассмотрение решений,
полученных для каждой из
составляющих.
Суммирование
составляющих в общем виде часто
бывает затруднительно и далеко не
всегда необходимо, так как уже на
основании дискретного спектра можно
судить о форме кривой и об основных
величинах, ее характеризующих.
Рассмотрим
второй этап, представляющий собой
основную часть расчета.
Если,
например, несинусоидальная ЭДС
представлена в виде суммы постоянной
и синусоидальных составляющих, то
источник несинусоидальной ЭДС можно
рассматривать как последовательное
соединение источника постоянной ЭДС
и источников синусоидальных ЭДС с
различными частотами.
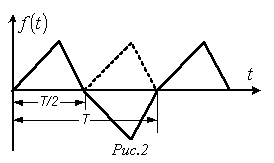
Так,
если ЭДС (рис. 12.13, а)
|
РАЗДЕЛ№ 51,1) Элементы, у которых ВАХ линейна, т. е. i= ku (k= const), называются линейными (рис. 1, а). Отношение R= u/i при этом называется сопротивлениемлинейного элемента. Определение. Зависимость тока через некоторый элемент (резистор, диод, лампочку) от напряжения на нем i(u) называется вольт-амперной характеристикой (ВАХ) этого элемента.
1,2)
Статическое сопротивление
Если
ВАХ HP имеет падающий участок, т. е.
такой участок, на котором увеличению
напряжения на
|

 ;
;  ;
; .
. .
(9.29)
.
(9.29) .(9.48)Закон
изменения тока в этом и предыдущем
случае один и тот же, только токи
отличаются знаками. Напряжение на
конденсаторе также изменяется по
подобному закону, только в этом случае
он заряжается (рис. 9.16 и 9.17).
.(9.48)Закон
изменения тока в этом и предыдущем
случае один и тот же, только токи
отличаются знаками. Напряжение на
конденсаторе также изменяется по
подобному закону, только в этом случае
он заряжается (рис. 9.16 и 9.17). (1)
(1) б)
б)
 .(На
верхнем пределе экспонента исчезает,
так как Re(s) = > 0).
Это — единственная из множества
формул преобразования Лапласа функций,
которую полезно запомнить.
.(На
верхнем пределе экспонента исчезает,
так как Re(s) = > 0).
Это — единственная из множества
формул преобразования Лапласа функций,
которую полезно запомнить.  по
определению. Отсюда следует, в
частности, что нижний предел в интеграле
Лапласа следует принимать равным
(– 0), что существенно лишь для
функций, неограниченных в начальный
момент времени — содержащих
слагаемое (t).
Обозначим соответствие оригинала и
изображения в символической
форме f(t) F(s).
Имеем
по
определению. Отсюда следует, в
частности, что нижний предел в интеграле
Лапласа следует принимать равным
(– 0), что существенно лишь для
функций, неограниченных в начальный
момент времени — содержащих
слагаемое (t).
Обозначим соответствие оригинала и
изображения в символической
форме f(t) F(s).
Имеем 
 .
(10.20)
.
(10.20) .
. .
. .
. -
постоянная составляющая или нулевая
гармоника;
-
постоянная составляющая или нулевая
гармоника; 

 ;
; .
.
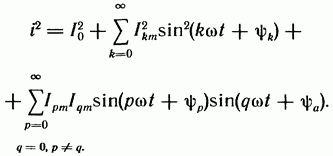

 При
отсутствии постоягной составляющей
При
отсутствии постоягной составляющей (12-42)
(12-42)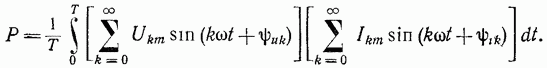


 (12-44)
(12-44)