FLOID

11

ЛАБОРАТОРНАЯ РАБОТА

ОПРЕЛЕЛЕНИЕ КРАТЧАЙШИХ ПУТЕЙ ПО МАТРИЧНОМУ МЕТОДУ И МЕТОДУ ФЛОЙДА

Цель работы – ознакомление с методами определения кратчайших путей в интегрированных вычислительных сетях.

Распределение каналов и потоков информации на линии связи производится с учетом длины пути. Для оценки длины пути используются различные критерии:

-число транзитных участков между взаимодействующими узлами коммутации (УК);

-протяженность пути;

-качество тракта передачи;

-надежность передачи и т. д.

Кратчайшим путем передачи информации называется путь, для которого критерий длины пути имеет наименьшее значение по сравнению с его значением для других возможных путей.

В теории потоков все методы выбора кратчайших путей основаны на утверждении о том, что если кратчайший путь _ij от произвольного УК _i к УК _j проходит через промежуточные УК_i1,…,УК _ik (рис. 1), то кратчайшие пути μ _i1,j,…,μ _ik,j от УК _i1,…, УК _ik к УК _j соответственно являются частями кратчайшего пути μ _i,j от УК _i к УК _j .

l _ik,j

l _i1,j

l _i,j

Рис. 1

Если длина пути m _i1,j равна L _i1,j ,то

L _i,j = L _i,i1 + L _i1,j .

Так как μ _i,j является кратчайшим, то

L_ε,j = min ( l _ε,ν + L _ν,j), (1)

^ν=i1,iN

где N -число узлов сети.

Для нахождения кратчайшего пути от узла ε к узлу j необходимо просмотреть все возможные пути и выбрать тот, у которого длина наименьшая.

Имеется ряд методов определения длины кратчайшего пути. Их можно разделить на две группы:

-методы нумерации узлов;

-матричные методы.

Матричный метод определения кратчайших путей позволяет найти длины кратчайших путей между всеми узлами сети одновременно и основывается на применении операций над матрицами расстояний.

Структуру сети связи с указанием длин ветвей можно описать в виде матрицы расстояний (длин) непосредственных связей

L = || l ¹ _i,j ||,hh

Элемент l¹_i,j определяет длину ветви β _i,j .

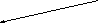
Пример. Пусть сеть связи имеет вид представленный на рис. 2.

30 15

20 15 15

20

20 20

15

25 10 25

40

Рис. 2

Цифры на ребрах и дугах соответствуют длинам ветвей. Тогда матрица расстояний будет

A B C D E F

A || 0 30 ∞ 20 ∞ ∞ ||

B || ∞ 0 15 15 ∞ ∞ ||

L¹ = C || ∞ 15 0 20 25 ∞ || (2)

D || 20 15 20 0 ∞ 25 ||

E || ∞ ∞ 25 10 0 40 ||

F || 15 ∞ ∞ 25 40 0 ||

Элементы главной диагонали равны 0, так как принимается, что расстояние внутри узла равно нулю. Если между парой узлов отсутствует ребро, то соответствующий элемент матрицы равен бесконечности (∞). Если между узлами i и j имеется дуга β¹_i,j , то элемент l¹_j,i также принимается равным бесконечности, например, l¹_A,F = ∞, тогда же l¹ _F,A =15. .

При анализе сетей передачи данных длину ветви удобно трактовать как задержку, которую вносит ветвь при передаче информации.

Матрица расстояний непосредственных связей неориентированной сети всегда симметрична относительно своей главной диагонали. Для ориентированной сети (как в примере) она может быть нессиметричной.

Возведем матрицу L¹ в квадрат L² = L¹*L¹ . Тогда

_N

l² _i,j = ∑ l¹_i,k * l¹_k,j = l¹_i,1*l¹_1,j + l¹_i,2*l¹_2,j +…+l¹_i,N*l¹_{N,j (3)}

^k=1

Можно интерпретировать умножение как последовательное соединение ветвей, а сложение как параллельное соединение ветвей.

Произведение l¹ _i,k*l¹ _k,j соответствует двухтранзитному пути (то есть пути проходящему через две транзитных ветви сети) от узла i_k к узлу j через узел k (рис. 3а), а сумма, например, трех произведений

l¹_i,i* l¹_i,j + l¹_i,j*l¹_{j, j} + l¹_i,k*l¹ _k,j

трем двухтранзитным путям (рис. 3б).

a

l¹_i,j l¹_k,j

б

l¹_i,i

l¹_i,j

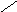
l¹_i,_j l¹ _j,j

l¹ _i,k l¹_k,j

Рис. 3

Произведения l¹_i,i*l¹_i,j и l¹_i,j *l¹_j,j фактически соответствуют однотранзитным путям, так как длина пути (задержка) внутри УК (то есть l¹_i,i и l¹_j,j ) не принимаются во внимание.

Для подсчета длины каждого из таких n транзитных путей необходимо операцию умножения заменить операцией сложения, то есть вместо l¹_i,k*l¹_k,j будем иметь l¹_i,k + l¹ _k,j .

При наличии нескольких параллельных одно- двухтранзитных путей (рис. 3б) для определения длины кратчайшего пути между узлами следует операцию сложения заменить операцией выбора из всех длин минимальной длины одно- двухтранзитного пути, то есть вместо (4) будем иметь

l²_i,j = min (l¹_i,k + l¹_k,j) = min |(l¹_i,j + l¹_1,j);(l¹_i,2 +l¹_2,j);…(l¹_i,N + l¹_N,j)|

^k=1,…,N

Таким образом элемент l² _i,j матрицы L² равен длине кратчайшего пути от УК_i к УК_j среди всех одно- двухтранзитных путей.

При возведении матрицы L¹ в r -ю степень при использовании этих операций получим матрицу

L^r = L^r-1*L¹ ,

элемент которой

l^r _i,j = min (l^r-1_i,k + l¹_k,j) = min |(l^r-1_i,1 + l¹_1,j);(l^r-1_i,2 + l¹_2,j);…(l^r-1_i,N + l¹_N,j)|

^{k = 1,…,N}

будет равен длине кратчайшего пути от УК_i к УК_j среди всех одно- двух- и т. д. r -транзитных путей.

При наличии на сети N узлов коммутации число транзитных ветвей в пути без петель не может быть больше N-1 . Следовательно, может потребоваться вычисление матрицы L^r, у которой r ≤ N-1.

Для конкретной сети может оказаться, что при r < N-1

L^r = L^r-1 . (4)

Так как при равенстве (4) всегда выполняется равенство L^r+1 = L^r, вычисление матрицы более высокой степени прекращается, если в процессе вычисления матриц встретится равенство (4).

Матрица L^r-1 при выполнении условия (4) называется дистанционной матрицей и обозначается

D = L^r-1 = L^r = || d _i,j || . (5)

Таким образом, элементы дистанционной матрицы равны длинам кратчайших путей между соответствующими узлами сети связи. Матрица часто называется матрицей расстояний (длин, задержек).

Для рассматриваемого примера вычислим l²_A,B

L²_A,B = min |(l ¹_A,A + l¹_A,B); (l¹_A,B + l¹_{B B}); (l¹_A,C + l¹_C,B ); (l¹_A,D + l¹_D,B);

(l¹_A,E + l¹_E,B);( l¹_A,F + l¹ _F,B)| =

= min |(0 + 30); (30 + 0); (∞ + 15); (20 + 15); (∞ + ∞);(∞ + ∞)|=

= min | 30; 30; ∞; 35,∞,∞ |=30 .

Аналогично вычислим остальные элементы матрицы L² , получим

A B C D E F

A || 0 30 40 20 ∞ 45 ||

B || 35 0 15 15 40 40 ||

L² = C || 40 15 0 20 25 45 ||

D || 20 15 20 0 45 25 ||

E || 30 25 20 10 0 35 ||

F || 15 40 45 25 40 0 ||

Затем

A B C D E F

A || 0 30 40 20 65 45 ||

B || 35 0 15 15 40 40 ||

L ³ = C || 40 15 0 20 25 45 ||

D || 20 15 20 0 45 25 ||

E || 30 25 20 10 0 35 ||

F || 15 40 45 25 40 0 ||

А затем

A B C D E F

A || 0 30 40 20 65 45 ||

B || 35 0 15 15 40 40 ||

L⁴ = C || 40 15 0 20 25 45 ||

D || 20 15 20 0 45 25 ||

E || 30 25 20 10 0 35 ||

F || 15 40 45 25 40 0 ||

Здесь L⁴ = L³, следовательно D = L³ .

Рассмотренные методы позволяют определить длину кратчайшего пути, но не указывают те ветви, которые входят в этот путь.

Определение самого кратчайшего пути связано с некоторой дополнительной процедурой.

Если для определения длины кратчайшего пути применяется способ нумерации узлов, то при выполнении дополнительной процедуры учитывается свойство веса УК_i . Это свойство заключается в том, что существует УК_{j ,} для которого выполняется равенство

W_i =l_i,j+W_j (6)

Отсюда следует, что

W_i – W_j = L_i,j (7)

Поэтому если выполняется условие (7), то кратчайший путь от УК_i проходит по ветви β_i,j . Переходя к УК_j , находим следующую ветвь, для которой выполняется последнее условие и которая также входит в этот кратчайший путь. Так, шаг за шагом можно определить все ветви, образующие кратчайший путь.

Исключив затем кратчайший путь из рассмотрения подобным образом определяются и другие пути от исходящего УК_i к входящему УК_j. Данный метод выбора кратчайших путей от одного узла до всех остальных узлов называется методом Флойда.

При матричном методе определения кратчайшего пути дополнительно к дистанционной матрице на основе матрицы длин непосредственных связей составляется так называемая матрица длин непосредственных связей Г, элементы главной диагонали которой в отличие от элементов l_i,j =0 имеют значения l_i,j =∞,где значком ∞ обозначена бесконечность. Таким образом, матрица Г легко может быть получена по матрице L¹ .

Пример

Для рассматриваемого случая

A B C D E F

A || ∞ 30 ∞ 20 ∞ ∞ ||

B || ∞ ∞ 15 15 ∞ ∞ ||

Г= C || ∞ 15 ∞ 20 25 ∞||

D || 20 15 20 ∞ ∞ 25||

E || ∞ ∞ 20 10 ∞ 40||

F || 15 ∞ ∞ 25 40 ∞ ||

Замена элемента l¹_i,i на l¹ _i,i = ∞ в матрице Г означает, что длина пути в УК_i принимается бесконечно большой. Это дает возможность не рассматривать все пути проходящие через исходный узел , то есть позволяет исключить путь (β_i,i , β _i,j), изображенный на рис. 3б. Полученная таким способом модернизированная матрица длин Г= ||γ _i.j || умножается на дистанционную матрицу D с использованием тех же операций, что и ранее. При умножении матрицы Г на матрицу D образуется матрица Δ = ГD, элементы которой используются для получения дисперсионных матриц (то есть матриц величин второго и т. д. кратчайших путей). Каждый элемент матрицы Δ= || δ _i,j || имеет вид

δ _i,j = min |(γ_i,1 + d_1,j);(γ_i,2 + d _2,j);…(γ _i,i + d _i,j);…(γ _i,N + d _N,j)| (8)

^k

В выражении (8) min означает, что минимум может браться для кратчайшего пути (к=1), второго по длине пути (к=2) и т. д. Каждый из членов (γ _i,e + d _e,j) = ∞ в выражении (8) определяет длину пути от узла i к узлу j ,если первым транзитным узлом после узла i на пути к узлу j будет узел ε, ε  (1,…,N). Если узел ε не является соседним узлом i, то

(γ _i,ε + d _ε,j) = ∞.

Так как γ _i,i = ∞, член (γ _i,i + d _i,j) будет всегда ∞. При этом элемент ( _i,j +d _j,j ) не обязательно равен ∞. Таким образом, число членов выражения (8), не равных бесконечности, равно числу n соседних УК, то есть числу исходящих из УК направлений (ветвей).

Член выражения (8), имеющий минимальное значение и определяющий длину кратчайшего пути от узла i к узлу j через узел ε

δ¹_i,j = min |( γ _i,1 + d _1,j);…( γ _i,N + d _N,j)|

¹

заносится в качестве элемента ¹_i,j в дисперсионную матрицу первого выбора Δ¹ = || δ ¹ _i,j ||. Второй по значению член выражения (8), определяющий длину второго по протяженности пути после кратчайшего от узла i к узлу j

δ ²_i,j = min |(γ _i,1 + d _1,j );…(γ _i,N + d _N,j)|

²

заносится в качестве элемента δ²_i,j в дисперсионную матрицу второго выбора Δ² = ||δ ²_i,j || ..

При наличии n соседних узлов можно получить n дисперсионных матриц ∆¹ ,…, ∆ⁿ .

Рассмотрим пример расчета элементов матриц  (  ¹, ²,…).

Пусть сеть связи имеет вид, представленный на рис. 2.

Тогда матрицы L ¹ и Г будут

A B C D E F A B C D E F

A|| 0 30  20   || A||  30  20   ||

B||  0 15 20   || B ||   15 20   ||

L¹= C ||  15 0 20 25  || Г= C ||  15  20 25  ||

D||20 15 20 0 ∞ 40 || D || 20 15 20   40 ||

E||   20 15 0 40 || E ||   20 15  40||

F|| 15   25 40 0 || F || 15   25 40  ||

Тогда, например, элемент δ_1,2¹ ,определяющий минимальный по протяженности путь от вершины A к вершине B матрицы Δ¹ согласно (8) будет

δ_1,2 ¹ = min [(γ_1,1 + d_1,2);(γ_1,2 + d_2,2);(γ_1,3 + d_3,2); (_1,4 + d_4,2); (γ_1,5 + d_5,2);

¹ (γ_1,6 + d _6,2)] =

= min [(∞ +30); (30 + 0); (∞ + 15); (20 +15); (∞ +25); (∞ +40) = 30

¹

Так как минимальное значение в выражении находится на втором месте, что соответствует вершине B, то в минимальном пути от вершины A к вершине B нет промежуточных вершин.

Элемент δ_1,2² матрицы Δ ² , соответствующий второму по протяженности пути от вершины A к вершине B, будет

δ _1,2 ² = min […. ] = 35.

²

Так как второе по минимуму выражение находится на четвертом месте, что соответствует вершине D, то второй по протяженности путь от вершины A к вершине B проходит через вершину D.

Выбрав кратчайшие пути от какого либо узла ко всем остальным, можно построить так называемое дерево кратчайших путей, в котором из всего множества путей от узла указаны только кратчайшие от него пути ко всем остальным узлам.

Например, для графа рис. 2, которому сопоставлена матрица L ¹ непосредственных связей, дерево кратчайших путей изображено на рис. 4.

Дерево кратчайших путей является поддеревом дерева путей (рис.5).

B

C

E

A

D

D

F

Рис. 4.Дерево кратчайших путей от вершины А

ко всем остальным вершинам

Замечание. Дерево кратчайших путей и дерево путей от узла ко всем остальным узлам для неориентированных графов (сетей) совпадает с деревом кратчайших путей и деревом путей соответственно от всех узлов к рассматриваемому узлу i. Для ориентированных графов (сетей связи) такого совпадения может и не быть.

F

E

D

F

E

F

F

D

D

C

E

D

F

B

F

F

C

F

E

F

D

F