27. Распределения Релея и Райса

Пусть

x и y

- независимые гауссовские случайные величины,

x

! mx ,

! my ,

!

! 2 . Требуется найти функцию распределения

(x # mx )2

( y # my )2

и

y

функцию плотности вероятностей величины % ! x2

y2 .

По определению

w% (& ) !

dF% (& )

,

d&

где F% (& )

- функция распределения, а

w% (& )

- функция

плотности

вероятностей случайной величины % .

Функция распределения определяется

как F% (& ) ! Pr[% & ] . С учетом определения случайной величины % имеем

F% (& ) ! Pr[x2 y2 & 2 ] !

(( wx ( )wy ())d d) ,

(27.1)

2 ) 2 & 2

где wx ( ) ,

wy ())

- функции плотности

вероятностей величин

x

и

y ,

определенные как

w ( ) !	1	0	#	(	m			)2 −	,
		exp.		#		2	x	+
x	21	.		2				+
		/						,
wy ()) !	1	0	#	() # my )2 −
		exp.				2		+ .
	21	.		2				+
		/						,

После подстановки этих выражений в (27.1) имеем

	1		0		( # m	x	)2 () # m		y	)2 −
F% (& ) ! ((			.	#							+
	21	2	exp.				2	2			+d d) .
2 ) 2 & 2			/							,

Рассмотрим показатель экспоненты в (27.2)

( # mx )2 () # my )2 ! 2 ) 2 mx2 m2y # 2mx # 2my)

(27.2)

(27.3)

Заменим в (27.3) прямоугольные координаты ( ,)) на полярные (3,2 ) ,																															имея в
виду что ! 3 cos2 , ) ! 3 sin2 , тогда
( # mx )2 () # my )2 ! 3 2												mx2 my2 # 2mx 3 cos2 # 2my 3 sin2 .																			(27.4)
Обозначим m2 ! mx2			my2 и используем соотношение
	Acos x B sin x !														A2					B2		cos(x # arctan(B / A)) ,
тогда (27.4) принимает вид
	( # mx )2							() # my )2										! 3 2 m2					# 23m cos(2 # 4) ,								(27.5)
где 4 ! arctan(my / mx ) .								После							подстановки										(27.5)			в	(27.2) и		замены
d d) ! 3d3d2 , 5 2 ) 2								& 2 6! 53 &, 0 2 216, имеем
				& 21				3						0				3 2 m2 # 23mcos(2 #4)											−
	F (&) !			( (						exp.					#														+d3d2	,
									2															2
	%							21						.									2						+
				0 0										/															,
или
		&	3					0		3	2			m					2	−0	1	21		0	3m				−	−
																				.										+
%	(&) !	(			2			.							2							( .				2	cos(2		+		(27.6)
																				+.										+
F							exp.#					2								+	21	exp		/				#4) d2		d3 .
		0						/												,/		0							,	,
Интеграл вида
								I0 (x) !						1			21 exp7x cos(2 #4)8d2 ,											4 - любое ,
												21
																	(0

называется функцией Бесселя первого рода нулевого порядка. Заметим, что

I0 (0) ! 1. Использование этого соотношения в (27.6) дает выражение для

функции распределения
&	3		0		3	2	m		2 −		0	3m −
F% (&) ! (			.						+
			exp.	#						+I0 .				+d3
		2				2		2					2
0			/						,		/			,

и функции плотности вероятностей

	&		0		&	2	m		2 −	0	&m −
w% (& ) !			.	#					+					& 9 0 .
		2						2		.		2	+,		(27.7)
			exp.			2			+I0
			/						,	/			,

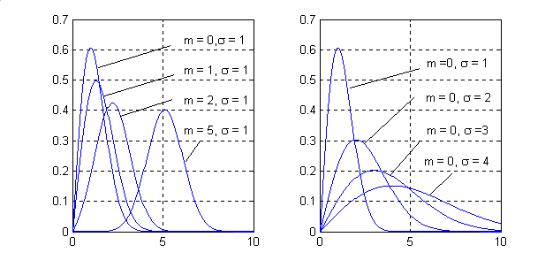
Плотность вероятностей (27.7) называется плотностью вероятностей Райса

(Rice). Она зависит от двух параметров m и . Если m ! 0 , то имеем частный

случай распределения Райса известный как распределения Релея (Rayleigh)

			&			0		& 2		−
w	%	(& ) !				exp.	#			+,	& 9 0 .
					2				2
						.		2		+
						/				,

Графики функции (27.7) для различных значений параметров m и показаны на рис.27.1

Рис.27.1 Плотности вероятностей Райса для различных значений параметров m и

28. Канал с замираниями. Модель с рассеивателями

Рассмотрим передачу ЧМ сигналов, si (t) 2E / T cos 2!fi t , 0 # t # T , i 0,1,2,..., q 1. Частоты сигналов fi выбраны так, чтобы сигналы были

ортогональны в усиленном смысле. Пусть был передан i -ый сигнал, на выходе канала с замираниями сигнал описывается как

r(t) 2E / T cos(2!fi t & ) % n(t) ,	(28.1)
где - случайный коэффициент передачи канала, ( 0 , &	- случайный

фазовый сдвиг, 0 ) & # 2! , n(t) - белый гауссовский шум. Модель канала с

замираниями относится к классу каналов со случайными параметрами,

которыми в данном случае являются величины и & . Величины и &

статистически независимы друг от друга и от шума. Случайный фазовый сдвиг распределен равномерно в интервале [0,2! ] , а коэффициент передачи канала распределен по закону Релея или Райса. Рассмотрим простую, но реалистичную модель, которая приводит к описанию (28.1).

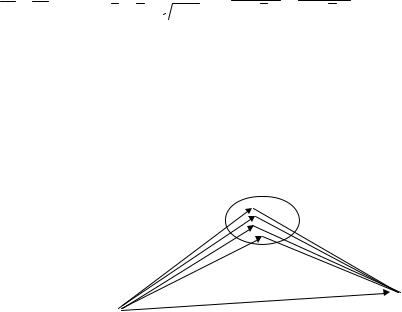
Пусть сигнал распространяется через передающую среду, которая может быть описана как множество рассеивателей (отражателей) (см. рис.28.1)

“Облако” рассеивателей

Передатчик

Приемник

Рис.28.1 Модель канала с рассеивателями

Тогда в отсутствие шума сигнал на выходе канала с рассеивателями может быть описан как

r(t) ck si (t + k ) ,	(28.2)
k

где ck коэффициент отражения k -го рассеивателя, + k задержка, вносимая k м рассеивателем. Подставляя в (28.2) выражение для сигнала, получаем, что

	r(t) ck		2E / T cos 2!fi (t + k ) ck 2E / T cos(2!fit ,ik ) ,					(28.3)
	k			k
где	,ik 2!fi+ k -		фазовый сдвиг, возникающий из-за задержки,				связанной с
распространением сигнала до и от k -го рассеивателя. Из (28.3) следует, что
	2		/	2	ck	/
	r(t) 0	ck cos,ik −		2E / T cos 2!fit % 0		sin,ik − 2E /T sin 2!fit
	1	k	.	1	k	.
			x	2E / T cos 2!fi t % y	2E / T sin 2!fi t ,			(28.4)
где использовано обозначение
				x ck cos,ik				(28.5)
				k
				y ck sin ,ik .				(28.6)
				k
Равенство (28.4) можно тогда переписать в виде
			r(t) 2E / T cos(2!fi t & ) ,					(28.7)
где	x2 % y2 ,		& arctan( y / x) . Случайные величины x и y				называются

квадратурными компонентами коэффициента передачи. Заметим, что амплитуда и энергия принятого сигнала даже в отсутствие шума случайны, в этом собственно и состоит смысл явления, называемого замираниями сигнала

(fading). Поэтому можно говорить о средней энергии принятого сигнала и

среднем отношении сигнал/шум. Средняя энергия принятого сигнала определяется как

E T5r 2 (t)dt T5r 2 (t)dt T5 2 3 2E / T cos(2!fi t & )42 dt

0 0 0

2	T53 2E / T cos(2!fit & )42 dt 2	E (		%		)E .
			x2		y2		(28.8)
	0

Правая часть равенства (28.7) при прибавлении всегда присутствующего шума совпадает с правой частью (28.1). Таким образом, модель с рассеивателями приводит к описанию (28.1). Для завершения рассмотрения модели с рассеивателями осталось дать статистическое описание случайных параметров канала и показать, что при некоторых разумных предположениях это распределение будет задаваться распределениями Релея и Райса.

Предположим, что а) рассеивателей много, б) они статистически независимы, и в) вклад каждого рассеивателя в суммы (28.5), (28.6) невелик.

При этих предположениях, можно считать распределения величин x и y

примерно гауссовскими независмо от того как были распределены образующие их слагаемые. Это следует из центральной предельной теоремы теории вероятностей. Поскольку x и y - гауссовские случайные величины, то для завершения их описания надо определить параметры их совместного распределения. Для гауссовских величин необходимо и достаточно определить только первые и вторые моменты. Для математических ожиданий имеем

x ck cos,ik ck cos,ik 0 ,

k

k

y ck sin ,ik ck sin ,ik 0 ,

k

k

так как

sin6

cos6

0

при равномерно

распределенном

аргументе 6 ,

0 ) 6 # 2! . Далее

il

ck cos,ik cl sin ,i l

xy

ck cos,ik cl sin ,

k

l

k

l

%

0

ck2

,

cos,ik sin ,ik

ck

cl

cos,ik

sin ,il

k

k

l7k

так как sin6 cos6 sin6 cos6 0 при равномерно распределенном аргументе 6 , 0 ) 6 # 2! . И наконец,

2

/2

2

/2

/

x

2

ck cos,ik

ck

cos,ik cl cos,il

0

ck cos,ik −

0

−0

cl cos,il −

1

k

.

1

k

.1

l

.

k

l

%

1

,

ck2

cos2 ,ik

ck2

ck

cos,ik

cl

cos,il

2

k

k

l7k

k

			2		/2		2		/2		/
y	2												ck sin ,ik cl sin ,il
		0		ck sin ,ik −		0		ck sin ,ik −0		cl sin ,il −
		1		k	.	1		k	.1	l	.			k c

%

1

,

ck2

sin 2 ,ik

ck2

ck

sin ,ik

cl

sin ,il

k

k

l7k

2

k

так как

1/ 2

при равномерно распределенном аргументе 6 ,

sin 2 6

cos2 6

0 ) 6 # 2! . Введем нормировку

k

1. При такой

ck2

нормировке средняя

принятая энергия равна энергии E , см. равенство (28.8).

Итак,

получено, что

x

и y

гауссовские случайные величины, и

0 ,

1/ 2.

x2

y2

Это значит, что они независимы и одинаково

x

y

xy

распределены с параметрами (0,1/ 2) . Отсюда следует, случайный коэффициент передачи канала x2 % y2 распределен по закону Релея.

Более общий случай, приводящий в итоге к замираниям,

распределенным по закону Райса, возникает когда x и y распределены по гауссовскому закону, независимы, имеют одинаковые дисперсии, но ненулевые математические ожидания. В этом случае можно положить, что как и прежде x2 % y2 1, но x y 8 / 2 , а (x x)2 ( y y)2 (1 8 ) / 2 , где величина 8 имеет смысл доли энергии сигнала, переданной по нерассеянной (регулярной)

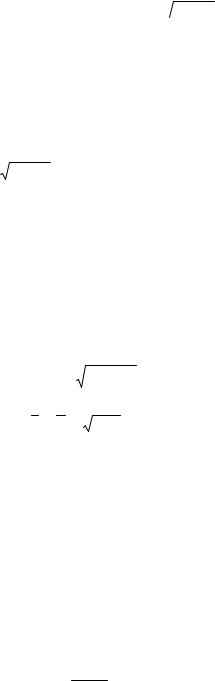
компоненте, 0 ) 8 ) 1, (см. рис.28.2)

“Облако” рассеивателей

Рассеянная компонента принятого сигнала

Передатчик	Приемник

Регулярая компонента принятого сигнала

Рис.28.2 Модель канала с рассеянной и регулярной компонентами

При 8 0 имеет место канал с релевскими замираниями (нет регулярной компоненты), а при 8 1 - канал с АБГШ и случайной фазой (нет рассеянной компоненты, то есть в канале нет замираний) .

29. Вероятность ошибки при передаче ЧМ сигналов по каналу с замираниями

Рассмотрим передачу ЧМ сигналов si (t) 2E / T cos 2!fi t , 0 # t # T , i 0,1,2,..., q 1, по каналу с замираниями. Частоты сигналов fi выбраны так,

чтобы сигналы были ортогональны в усиленном смысле. Пусть был передан i -й

сигнал; на выходе канала с замираниями сигнал описывается как

r(t) 2E / T cos(2!fi t & ) % n(t) ,	(29.1)
где - случайный коэффициент передачи канала, ( 0 , &	- случайный

фазовый сдвиг, 0 ) & # 2! , n(t) - белый гауссовский шум. Случайный фазовый

сдвиг распределен равномерно в интервале [0,2! ] , а коэффициент передачи

канала распределен по закону Райса. Случайный коэффициент передачи канала

может быть представлен

в виде

x2 % y 2 ,

где x

и y - независимые

x y

/ 2 , а

(1 ) / 2 ,

гауссовские с.в. с параметрами

(x

)2

( y

)2

x

y

где величина имеет

смысл

доли

энергии

сигнала,

переданной по не

рассеянной (регулярной) компоненте, 0 ) ) 1.

Оптимальный приемник для канала с замираниями совпадает в рассматриваемом случае с оптимальным приемником для канала с АБГШ и случайной фазой, рассмотренным ранее. Вероятность ошибки при передаче по каналу с замираниями может быть вычислена как

Pe Pe ( ) ,

где Pe ( ) - вероятность ошибки при фиксированном значении коэффициента

передачи канал , черта сверху означает усреднение по случайным параметрам канала. При фиксированном значении коэффициента передачи канала энергия

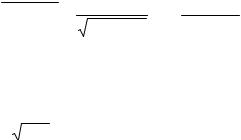
принятого сигнала равна 2 E . Поэтому условная вероятность ошибки Pe ( )

равна вероятности ошибки при передаче ЧМ сигналов по каналу со случайной

фазой при замене E на 2 E , то есть

q 1

1

1

l

2 E .

P ( )

+

C l

(1)l %1

exp/

,.

e

q 1

1% l

/

,

l 1

0

l %1 N0 −

Отсюда следует,

что

q 1

1

1

l

2 E .

P

+

C l

(1)l %1

exp/

, .

(29.1)

e

q 1

1% l

/

l %

,

l 1

0

1 N0 −

Рассмотрим среднее в выражении (29.1). Для него можно записать, что

1

l 2 E .

1

l (x2 % y 2 )E .

1

l x2 E .

1

l y 2 E .

exp/

,

exp/

,

exp/

, exp/

,.

/

,

/

l %1

N0

,

/

,

/

,

0

l %1 N0 −

0

−

0

l %1 N0 −

0

l %1 N0 −

(29.2)

поскольку x и y

независимы.

Ранее приводилась следующая лемма.

Лемма. Пусть x

- гауссовская случайная величина , распределенная с

параметрами (m,2 2 ) , 3 - постоянная, такая что 3 # 1/(22 2 ) . Тогда

exp(3x2 )

1

1

3m

2

.

2

exp/

2

, .

1

232

/

,

01 232

−

Применяя

лемму

к

вычислению

средних

в

(29.2)

со

значениями

3 lE / N0 (l %1) , m

/ 2 , 2 2

(1 ) / 2 , имеем

1

l x2 E .

1

l y 2 E .

exp/

,

exp/

,

/

,

/

l %1 N0

,

0

l %1 N0 −

0

−

		1		1		l E / N		.
				exp/			0	, .
	l			/				,
1%		(1	)E / N0	0		2(1% l % l(1 )E / N0 ) −
	1% l

Подстановка этого выражения в (29.2) и далее в (29.1) приводит к окончательному выражению

q 1

1

1

l E / N

0

.

P

+

C l

(1)l %1

exp/

, .

e

q 1

1% l % l(1

)E / N0

/

,

l 1

0

1% l % l(1 )E / N0 −

Рассмотрим некоторые частные случаи.

Пусть q 2 , тогда

1

1

E / N

0

.

P

exp/

, .

e

2 % (1

)E / N0

/

2 %

(1 )E / N0 )

,

0

−

Для двух крайних случаев 0 и 1 имеем соответственно

Pe

1

2 % E / N0

и

1

e

E

P

2 N0 .

e

2

Сравнение этих выражений показывает, что в канале с релеевскими замираниями (при 0 ) вероятность ошибки убывает с ростом отношения сигнал/шум очень медленно (обратно пропорционально). При отсутствии замираний (при 1) вероятность ошибки убывает с ростом отношения сигнал/шум гораздо быстрее (экспоненциально). Примерно такие же соотношения имеют место и для недвоичных сигналов.

Графики вероятности ошибки для различных значений параметров показаны на рис.29.1-29.4.

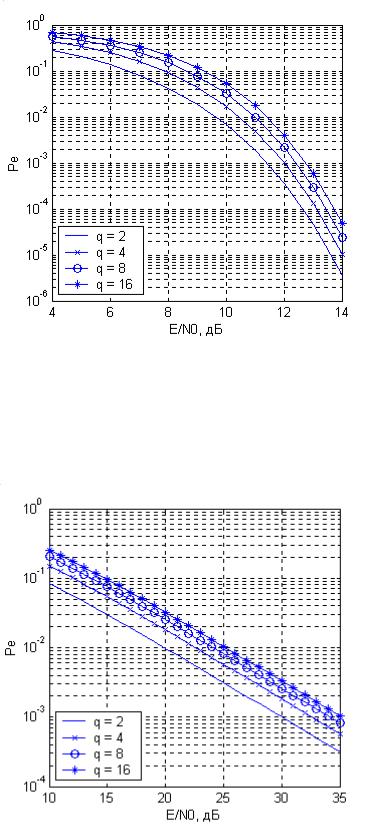
Рис. 29.1 Вероятность ошибки при передаче ЧМ сигналов по каналу с АБГШ и случайной фазой ( 1) .

Рис. 29.2 Вероятность ошибки при передаче ЧМ сигналов по каналу с релевскими замираниями ( 0) .

Рис. 29.3 Вероятность ошибки при передаче ЧМ сигналов по каналу с райсовскими замираниями ( 0.8) .

Рис. 29.4 Вероятность ошибки при передаче двоичных ЧМ сигналов

30. Передача с разнесением по каналу с замираниями. Перемежение

Рассмотрим передачу двоичных ЧМ сигналов si (t) = 2E / T cos 2πfi t , 0 < t < T , i = 0,1, по каналу с релеевскими замираниями. Частоты сигналов f0 и

f1 выбраны так, чтобы сигналы были ортогональными в усиленном смысле.

Вероятность ошибки в этом случае равна

	Pe =		1	.
		2	+ E / N0

Это выражение показывает, что в канале с релеевскими замираниями вероятность ошибки убывает с ростом отношения сигнал/шум очень медленно

(обратно пропорционально). Улучшить соотношение между величиной

отношения сигнал/шум и вероятностью ошибки можно, если применить передачу с разнесением.

Передача с разнесением состоит в том, что энергия передаваемого

сигнала делится на L частей и сигнал передается по L независимым подканалам (ветвям разнесения).

Ветви разнесения могут быть организованы:

а) во временной области; в этом случае имеет место временное разнесение;

б) в частотной области; в этом случае имеет место частотное разнесение;

в) во временной и в частотной области; в этом случае имеет место

частотно-временное разнесение.

Во всех случаях при передаче с разнесением в L раз снижается удельная

скорость передачи. Действительно,	удельная скорость	определяется	как
Vуд =V /W , V скорость передачи,	W полоса частот.	При использовании

двоичной ЧМ и передаче без разнесения V =1/ T , а W = 3 / T , то есть Vуд =1/ 3 .

При L -кратном разнесении имеем	Vуд =1/(3L) ,		так как при	временном
разнесении скорость уменьшается в L раз, а при		частотном разнесении в L раз
расширяется полоса частот.
Пусть сигнал, приходящий в	приемник	по	l -ой ветви	разнесения,
l =1,2,..., L , имеет вид
r (l ) (t) = µ(l ) 2(E / L) / T cos(2πfi t −θ (l ) ) + n(l ) (t) ,				(30.1)

i = 0,1. В этом равенстве учтено, что энергия сигнала разделена поровну между

L ветвями разнесения. Обозначим через rci(l ) скалярное произведение сигнала

принятого в l -й ветви разнесения		и	2 / T cos(2πf				t) , а через	r (l )	скалярное
						i		si
произведение сигнала принятого в			l -й ветви разнесения и					2 / T sin(2πfi t) ,
i = 0,1, l =1,2,..., L . Пусть приемник вычисляет величины
X 0 = ∑L ((rc(0l ) )2 + (rs(0l ) )2 ),
	l =1
и
X1 = ∑L ((rc(1l ) )2 + (rs(1l ) )2 )
	l =1
и формирует решение по правилу
)	0,	если X		0	> X	1 .
i	=
	1,	если X 0			< X1

Приемник, принимающий решение по такому критерию, называется приемником с аналоговым квадратичным сложением.

Вероятность ошибки вычисляется как обычно для равновероятных сигналов

Pe = (Pe (0) + Pe (1)) / 2 .

Найдем Pe (0) . Эта вероятность равна

			Pe (0) = Pr[ X1		> X 0 | 0] .				(30.2)
При передаче нулевого сигнала имеют место соотношения
	(r (l ) )2	+ (r (l ) )2 = (x(l )		E / L + n(l ) )2		+ ( y(l )	E / L + n(l ) )2 ,		(30.3)
	c0		s0		c0			s0
			(r (l ) )2 + (r (l ) )2		= (n(l ) )2 + (n(l ) )2 ,				(30.4)
			c1	s1	c1	s1
где x(l ) , y(l )	гауссовские компоненты коэффициента передачи канала								в l -й
ветви разнесения µ(l ) ,			nci(l ) , nsi(l ) -	скалярные произведения шума в l -й ветви
разнесения и	cos	и	sin i -й частоты		соответственно, i = 0,1, l =1,..., L . В
релеевском канале с независимыми ветвями разнесения x(l ) ,								y(l ) - независимые
гауссовские с.в. с нулевым средним и дисперсией 1/ 2 ,							nci(l ) ,	nsi(l ) - независимые

от них и независимые между собой гауссовские с.в. с нулевым средним и

дисперсией N0 / 2 .

Чтобы

оценить

вероятность (30.2) применим

границу

Чернова

Pr[ X1

> X 0 | 0] <

exp(λ( X1 − X 0 )),

где λ - параметр оценки Чернова,

λ > 0 . Используя определения

(30.3) и

(30.4), получим, что

Pe (0) < ∏L

exp(− λ(x(l )

E / L + nc(l0) )2 )

exp(− λ( y(l ) E / L + ns(l0) )2 )×

l =1

×∏L

exp(λ(nc(1l ) )2 )exp(λ(ns(1l ) )2 )

(30.5)

l =1

При записи этого выражения учтена независимость ветвей разнесения и независимость шума от случайного коэффициента передачи канала.

Ранее приводилась следующая лемма.

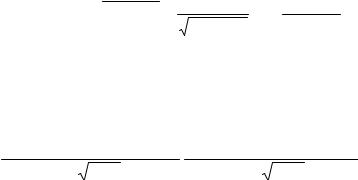
Лемма. Пусть x - гауссовская случайная величина, распределенная с

параметрами (m,σ 2 ) , α - постоянная, такая что α <1/(2σ 2 ) . Тогда

			1			αm	2
exp(αx	2	) =						2
			1 − 2ασ 2	exp	1	− 2ασ			.

Применяя лемму к вычислению средних в (30.5) со значениями α = −λ ,

	m = 0 , σ 2 = (E / L + N0 ) / 2 , имеем
	exp(− λ(x(l ) E / L + nc(l0) )2 )		exp(− λ( y(l ) E / L + ns(l0) )2 )=											1	,
												1		+ λ(E / L + N0 )
	далее, применяя эту же лемму со значениями α = λ , m = 0 , σ 2													= N0 / 2 , имеем
									1	.
		exp(λ(nc(l0) )2 )			exp(λ(ns(l0) )2 )=
							1
									− λN0

Здесь возникает дополнительное ограничение на параметр границы Чернова:

λ <1/ N0 .

Подстановка этих выражений в (30.5) дает оценку

			1			1	L
								,	(30.6)
Pe (0) <			+ λ(E / L + N0 ) 1
	1					− λN0

где 0 < λ <1/ N0 . Отыскание значения параметра λ , оптимизирующего оценку

(30.6), сводится к максимизации знаменателя, то есть к решению уравнения

	d	(1 + λ(E / L + N0 ))(1 −λN0 ) = 0 ,
	dλ
или
(E / L + N0 )(1 − λN0 ) − (1 + λ(E / L + N0 ))N0 = 0
откуда находим
		λ =	1		E / L		.
			2 (E / L + N
						0 )N0

Подставляя это значение в (30.6) имеем наиболее точную границу Чернова

L

1

1

P (0)

<

.

(30.7)

e

1

+

E

1 −

E / L

2N0 L

2(E / L +

N0 )

Упростив (30.7) и приняв во внимание, что в данном случае условная вероятность ошибки совпадает с безусловной, имеем окончательное выражение

				E				L
					+
		4					1
P	<			LN0				.	(30.8)
							2
e				E
					+ 2
			LN0

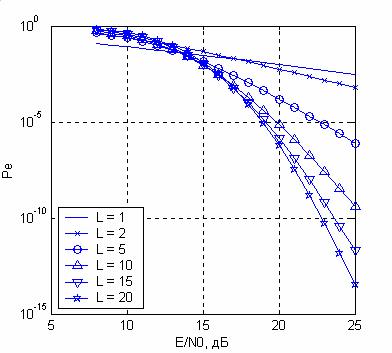
Графики верхней границы вероятности ошибки, вычисленной по формуле

(30.8), показаны на рис.30.1. Для L =1 приведено точное значение вероятности ошибки Можно показать, что для каждого значения отношения сигнал/шум существует

Рис.30.1 Вероятность ошибки при двоичной передаче с разнесением в канале с релеевскими замираниями

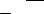
оптимальное число ветвей разнесения. Оно может быть найдено численно и

оказывается равным L ≈ (E / N0 ) / 3 . Если подставить это значение в (30.8), то

получится выражение для оценки вероятности ошибки, оптимизированной по числу ветвей разнесения. Оно имеет вид

−0.149	E
P < e	N0 .
e

Отсюда следует, что в канале с релеевскими замираниями при передаче с

оптимальным разнесением вероятность ошибки убывает с ростом отношения сигнал/шум экспоненциально. Напомним, что в канале без замираний вероятность ошибки равна

= 1 − E

Pe 2 e 2 N0 .

Сравнение этих выражений показывает, что в канале с релеевскими

замираниями и оптимальным разнесении проигрыш в отношении сигнал/шум составляет величину около 5.25 дБ ( =10 log10 (0.5 / 0.149) ) и не возрастает

бесконечно, как при передаче без разнесения. Серьезным недостатком при передаче с оптимальным разнесением является сильное убывание скорости передачи (и/или увеличение полосы частот) с ростом отношения сигнал/шум.

Легко показать, что удельная скорость передачи меняется как

Vуд =1/(3L) = (E / N0 )−1 . Это ухудшение удельной скорости передачи в L раз

(т.е. в (E / N0 ) / 3 раз при оптимальном разнесении) зачастую препятствует

применению оптимального разнесения на практике. На рис.30.2 приведены иллюстрирующие графики.

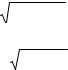
Рис.30.2 Вероятность ошибки и удельная скорость передачи при передаче по релеевскому каналу с оптимальным разнесением и при передаче по каналу без замираний.

31. Сравнительная характеристика методов передачи в радиоканалах

Рассмотрим передачу двоичных сигналов si (t) , 0 < t < T , i = 0,1, по

каналам, которые могут быть заданы следующими моделями:

-канал с АБГШ;

-канал с АБГШ и случайной фазой;

-канал с релеевскими замираниями.

Эти модели могут использоваться для описания условий передачи по различным радиоканалам. В рамках перечисленных моделей могут использоваться различные виды модуляции и приема, рассмотренные в предыдущих разделах курса.

В таблице 31.1 приводятся основные характеристики некоторых методов передачи применительно к перечисленным моделям. На рис.31.1 показаны графики зависимости вероятности ошибки от отношения сигнал/шум для этих каналов и видов модуляции. Наилучшую зависимость обеспечивает ФМ в канале с АБГШ. В каналах со случайной фазой ФМ неприменима. В канале со случайной фазой наилучшую зависимость между отношением сигнал/шум и вероятностью ошибки дает ОФМ. Следует подчеркнуть, что использование ОФМ ограничено каналами с медленно меняющейся случайной фазой. При

быстрых изменениях случайной фазы при переходе от одного сигнального интервала к другому применение ОФМ невозможно. В этом случае возможна передача с использованием ЧМ, которая, вообще говоря, проигрывает ФМ и ОФМ по эффективности использования отношения сигнал/шум и по эффективности использования спектра (удельной скорости). Условия передачи по каналу с замираниями оказываются наиболее тяжелыми. Уменьшение

вероятности ошибки при передаче по каналу с замираниями требует

значительных энергетических затрат. Используя передачу с разнесением, можно

улучшить зависимость между отношением сигнал/шум и вероятностью ошибки.

При этом существенно снижается удельная скорость передачи. Особенно

сильное снижение удельной скорости передачи имеет место при оптимальном

разнесении.

Таблица 31.1

Канал,

Вероятность

Проигрыш

Удельная

Вид модуляции,

ошибки,

Pe

в отношении

скорость

прием

сигнал/шум, дБ

передачи,

Vуд

АБГШ, ФМ,

когерентный прием

Q(

2E / N0 )

0

1/2

АБГШ, ЧМ,

З дБ по сравнению с

когерентный прием

Q(

E / N0 )

ФМ в канале с АБГШ

1/3

АБГШ + сл.фаза, ЧМ,

1

−

2 N0

≤ 1 дБ по сравнению с

1/3

Некогерентный прием

ЧМ в канале с АБГШ;

E

e

≤ 4 дБ по сравнению с

2

ФМ в канале с АБГШ

АБГШ + сл.фаза,

1

−

N

≤ 1 дБ по сравнению с

1/2

(медленно изменяю-

ФМ в канале с АБГШ

E

щаяся), ОФМ,

e

0

2

некогерентный прием

Релеевские замирания,

проигрыш →

∞

при

ЧМ,

1

E / N0 → ∞ , по

Некогерентный прием

2 + E / N0

сравнению с ЧМ в

1/3

канале без замираний

Релеевские замирания,

E

L

проигрыш →

∞

при

ЧМ, некогерентный

4

1+

E / N0 → ∞

, по

прием, L-кратное

LN0

сравнению с каналом

разнесение

1/(3L)

E

2

без замираний, но

2

+

медленнее, чем при

LN0

отсутствии разнесения

Релеевские замирания,

проигрыш около

ЧМ, некогерентный

e

5.25 дБ по сравнению с

1/(E / N0 )

прием, оптимальное

− 0.149 E / N0

ЧМ в канале без

разнесение,

замираний

( L = (E / N0 ) / 3 )

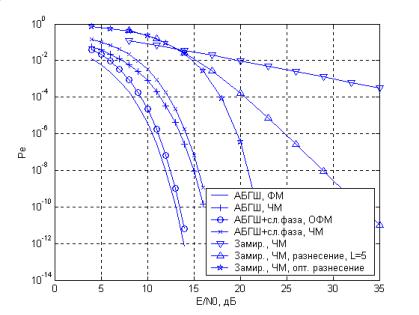
Рис.31.1 Зависимость вероятности ошибки от отношения сигнал/шум для различных каналов и видов модуляции.