2484

	4
e)	∫ 3			4 − 3xdx ;
	1
	∞			dx
f)	∫					.
				+ 5x
	0 2
5.8. a) ∫	2x2 + 3 + x4 x								dx ;
				3		x
b) ∫ arcsin					4
						2x dx ;
				1− x
c) ∫(4 − x)e2 x dx ;
d) ∫				x + 1			dx ;
			x3 + x
	0
e)	∫			1 − 6xdx ;
	−4
	∞			4dx
f)	∫1							.
		(x + 2)8

5.9. a) ∫1+ x3 − 5x3 x dx ; x

b)∫ arctg5 x dx ;

1+ x2

c)∫ xcos 54 xdx ;

d) ∫	x2 dx	;
	(x2 −1)(x + 1)
e) ∫2	4x + 1dx ;
0

∞ dx

f)∫1 (3 − 4x)2 .

5.10.a) ∫ 3x2 − 5x + 2dx ;3 2

x

b) ∫1 x2x3 dx ;

+

c)∫ xsin 54 xdx ;

d)∫ 4x2 + 3x − 3 dx ;

x3 − x

e)∫1 3 6x + 2dx ;

0

∞ dx

f) ∫ .

1 3 x

e) π∫ x sin xdx ;

0

f)

∞ arcsin x + 1

∫

1 − x

2

dx .

1

2

5.18 a) ∫ x3 − 3 x + 5 dx ;

x

b) ∫

2tgx + 3

dx ;

cos2 x

c) ∫(2x + 4)e2x dx ;

d) ∫

1

dx

;

(x2 + 2)(x −1)

e)

∫3

3 1 − 3x dx ;

0

f)

∞

3

xdx .

∫ ln

1

x

5.19 a) ∫

5x

3 − 3 x + 2

dx ;

x

b)∫ecos x sin xdx ;

c)∫(4x + 1)sin 45xdx ;

d) ∫ 2x − 5 dx ;

(x2 + 4)(x + 4)

e)	∫2		3	4 + 2x dx ;
	−6
	∞			x
f)	∫				dx .
			x	2
	1			+ 1
5.20 a) ∫				x3 − 2x		4 + 3	dx ;
					x

b)∫ 3 lnx x dx ;

c)∫arctgxdx ;

d) ∫			3x + 10
						dx ;
	(x2 + 5)(x + 2)
e) ∫1		e x			x dx ;
0		1 + e
∞		e	x
f) ∫					dx .
		3 + e		x
0

1				x
e) ∫							dx ;
		1 + x				2
0
∞				x − 3
f) ∫								dx .
		x	2	− 3x + 5
1
5.28 a) ∫				4		3	− 3x dx;
	5 +				x2
					x

b)∫ cos3 5x sin 5xdx ;

c)∫(x + 4)e− 2xdx ;

x+ 1

d)∫ (x + 2)(x2 − x) dx ;

e) ∫2

x2

3

dx ;

0

1 + x

∞

4

f) ∫

dx .

(5x −

2)

6

1

5.29 a) ∫

(2 +

x − 3x5 )

dx;

x

4

tg

4

b) ∫

x

dx ;

2

cos

x

c) ∫(3x − 2)sin 4xdx ;

d) ∫

x + 2

dx ;

(x − 3)(x

2

+

7)

e) ∫4

2x + 1dx ;

0

∞

x3

f) ∫

dx .

x

4

+ 3

1

5.30 a) ∫

5

x

6

−

2x

5

+ 1 dx ;

x

b) ∫

ln(x + 1) dx ;

x + 1

c) ∫(x + 3)e− x dx ;

d) ∫

2x − 5

dx

;

x(x2 + 8)

e) ∫5

x

dx ;

x

2

3

0

+

∞

dx

f) ∫

.

(6 −

5x)

2

1

11

Дифференциальные уравнения. Ряды

№№ 6.1-6.30. Найдите общее решение дифференциального уравнения первого порядка.

6.1. a) x(1 + y2 )dx + y(1 − x2 )dy = 0 ;

6.16. a) x 2 y′ = (1 + y 2 )(1 + x) ;

b)

′

2y

3

b) xy′ − y = − x2 + x .

y

−

x = x .

6.2. a) (1 + y2 )dx − xydy = 0 ;

6.17. a) x

2

y

′

−

y + 1

= 0

;

b) y

′

y

e x

xy

+ x

= x .

b) xy′ + y = x 2 + x .

6.3. a) y

′

1 + y2

6.18 a) e4 x y′ = 1 + y 2 ;

= 1 + x2 ;

b) xy′ + y = xex

2

.

b)

xy′ −

2 y =

2x

4

.

6.4. a) (e2 x + 5)dy + ye2 x dx = 0 ;

6.19. a) xy′ + (x 2 − 1)

1 − y 2 = 0 ;

b) xy′ − 2 y + x2 = 0 .

b) y

y

2

′

= x .

− x

6.5.a) x( y2 − 4)dx + ydy = 0 ;

b)xy′ + y = x + 1.

6.6.a) xyy′ = 1 − x2 ;

b)y′ − y tg x = sin 2x .

6.7.a) 2xdx − ydy = yx2 dy − xy2 dx ;

b)xy′ + 2 y = x3 .

6.8.a) yy′ + x = 0 ;

b)xy′ + 2 y = x4 .

6.9.a) xy′ = (1− x2 ) y ;

b)y′ − 2xy = x2 .

6.10.a) 4 − x2 y′ + xy2 + x = 0 ;

b)y′ c osx − y sin x = 1.

6.11.a) xy′ = cosx + 1y ;

b)xy′ + y = x 2 .

6.12a) x 2 y′ − (x − 3) sin 2 y = 0 ;

b)y′ + sin x y = x 2 ecos x .

− x				1
6.13. a) e		y	′			;
				= sin 3y				.
b) y	′	−	1 + x 2 = xe
				y			arctgx

6.20. a) (1 + x) y′ = x 1 − y 2 ;

b)

1

y′ +

y =

ecos x

.

sin x

x 2 sin x

6.21. a)

′

1

x + 1y

=

y − 1 ;

b)

′

y

2

arctgx

.

y

= (1 + x )e

− 1

+ x 2

6.22.a)sin y cos y y′ = 12 cos x ;

b)y′ + xy = 1 − x .

6.23.a) yy′ + ( y 2 + 1) cos 6x = 0 ;

b)xy′ − y = x 2 + x .

	6.24. a)	(1 − y) y						y
						′	= cos 2 x ;
									ectgx
	b)		′			y
		y		+ sin			2 x	= sin 2 x .

6.25.a)5− x y y′ = (1 − y)2 x ;

b)y′ + xy = 1 −1 x .

6.26.a) y′ sin y cos y = 2 1 x ;

b)xy′ + y = cos 4x .

	6.27. a) (1 + y) y				=			y 2
				′			1 + x 2 ;
		′						x
	b) xy		+ y	= 1 + x .

6.28. a) e2 x y′ = 1 + y 2 ;

y

b) sin 2 x y′ + y = x sin 2 xectgx .

12

6.14.a) xy′ = 1 + y 2 ;

b)y′ − xy = x .

6.15. .a)				′			1 − y 2
	tgx y				=		cos x ;
b)	y				y	x	=	ectgx
		′	+ sin 2					1 − x 2 .

6.29. a) (1 − y 2 ) y′ = 1 + y	;
1 − x	2

b)y′ − xy = 1 − x 2 .

6.30.a)tgy y′ = ( x + x 2 ) sin 2 y ;

b)(1 + x 2 ) y′ − y = (1 + x 2 )(1 − x)earctgx .

№№ 7.1-7.30. Для данного дифференциального уравнения второго порядка

найдите частное решение, удовлетворяющее заданным начальным условиям.

7.1.

y′′ − 6 y′ + 9 y = x2 − x + 3 ;

y(0) = 4 3 ;

y′(0) = 127 .

7.2.

y′′ − 3y′ + 2 y = 2x2 ;

y(0) = 0;

y′(0) = 0.

7.3.

y

′′

− 4 y

′

− 5y = 5x − 3 ;

y(0) = 2;

y (0) = -1.

′

7.4.

y′′ − 10 y′ + 24 y = 4x ;

y(0) = 0;

y′(0) = 3.

7.5.

y′′ + 3y′ −10 y = 10x2 + 4x − 5 ;

y(0) = 1;

y′(0) = 1.

7.6.

y

′′

− y

′

− 2 y = 4x

;

y(0) = 1;

′

2

y (0) = 1.

7.7.

y′′ + 2 y′ + y = 12x2

+ 6x − 4 ;

y(0) = 0;

y′(0) = 1.

7.8.

y

′′

+ 2 y

′

− 3y = 6x

− 3x + 2 ;

y(0) = 1;

′

2

y (0) = 1.

7.9.

y′′ − 3y′ + 2 y = x2 + x ;

y(0) = 2;

y′(0) = 1.

7.10.

y

′′

− 5y

′

+ 6 y = x

− x ;

y(0) = 1;

′

2

y (0) = 0.

7.11.

3y′′ − 2 y′ − 8y = − x2 + x ;

y(0) = 1;

y′(0) = 0.

7.12.

y′′ − 8y′ + 16 y = 3x 2

− x + 1;

y(0) = 0;

y′(0) = 1.

7.13.

y

′′

− 6 y

′

+ 13y = x

+ 2x + 3 ;

y(0) = -1;

′

2

y (0) = 2.

7.14.

y′′ + 5y′ − 6 y = 2x 2

− x − 3;

y(0) = 2;

y′(0) = 0.

7.15.

y

′′

− 2 y

′

+ 5y

= −3x

+ x + 2 ;

y(0) = 0;

′

2

y (0) = -2.

7.16.

y′′ + 4 y′ + 4 y = −2x 2

+ 3x − 1;

y(0) = -2;

y′(0) = -1.

7.17.

y

′′

+ 5y

′

+ 6 y

= − x

− 2x ;

y(0) = 1;

′

2

y (0) = 0.

7.18.

y′′ + 6 y′ + 9 y = 3x 2

− x − 2 ;

y(0) = 0;

y′(0) = 1.

7.19.

y′′ − 4 y′ + 13y = x 2

+ 4x + 1;

y(0) = 1;

y′(0) = 2.

7.20.

y′′ − 10 y′ + 25y = 2x 2

− 3x + 3;

y(0) = 2;

y′(0) = 0.

7.21.

y′′ − 6 y′ + 8y = −3x 2

+ x − 3 ;

y(0) = 0;

y′(0) = -2.

7.22.

y

′′

+ 2 y

′

+ 5y

= −2x

+ 4x + 2 ;

y(0) = -2;

′

2

y (0) = -1.

7.23.

y′′ + 6 y′ + 8y = − x 2

+ 2x + 3 ;

y(0) = 1;

y′(0) = 0.

7.24.

y

′′

+ 2 y

′

+ 2 y

= −2x

+ x + 1;

y(0) = 0;

′

2

y (0) = 1.

7.25.

y′′ − 12 y′ + 36 y = 2x 2

− x − 3 ;

y(0) = -1;

y′(0) = 2.

7.26.

y′′ + 4 y′ + 5y = x 2

+ 3x − 1;

y(0) = 2;

y′(0) = 0.

7.27.

y′′ + 3y′ + 2 y = 3x 2

− 2x + 1;

y(0) = 0;

y′(0) = -2.

7.28.

y′′ + 4 y′ + 20 y = −3x 2

+ x + 2 ;

y(0) = -2;

y′(0) = 1.

7.29.

y

′′

+ 10 y

′

+ 25y = − x

+ 3x − 2 ;

y(0) = 1;

′

2

y (0) = -1.

7.30.

y′′ + y′ − 2 y = −2x 2

+ 4x + 3 ;

y(0) = 0;

y′(0) = 2.

13

№№ 8.1-8.30. Исследуйте числовой ряд на сходимость.

∞

1

5n + 1 n

8.1. ∑

.

3

n

n=1

2n − 1

∞

1 n + 1 n

8.2. ∑

.

2

n

n

n=1

∞

1

8.3. ∑

.

n ln

2

n=2

n

∞

1

8.4. ∑

.

(n +

1) ln(n +

1)

n=1

∞

8.5. ∑

n + 1

.

n

n=1

2

n!

∞

2

n

(n

2

+ 1)

8.6. ∑

.

n!

n=1

∞

2

n .

8.7. ∑ sin

2

n=1

n

∞

3 +

4n

8.8. ∑

.

n

n=1

5

n

∞

2

3

n

8.9. ∑

n

.

n=1

(n + 2)!

∞

5

n

(n + 1)!

8.10. ∑

.

n=1

(2n)!

∞		2		+ 2
8.11. ∑			n			.
			3
n=2 n				− 4
∞		2n		+ 1
8.12. ∑								.
		3		n
n=1
∞		3n + 4						1
8.13. ∑									.
								n+1
n=1		2n + 3						2

∞1

8.14.∑n=1 (n + 2) ln2 (n + 2) .

∞2n−1

8.15.∑ n .n=1

	∞	5n		− 1
	8.16. ∑				e−n+3 .
		3		+ 3
	n=1	4n
	∞		1 .
	8.17. ∑
	n=2	n ln n
	∞			3n−1
	8.18. ∑					.
		2	n−1	(2n − 1)
	n=1

8.19. ∑∞ ( n2 + 2)n 42n .

n=2 3n + 2

∞n

8.20.∑ 2n + 1 .2n=1

	∞	2n − 1 .
	8.21. ∑
	n=1		n3n
	∞		n + 1			1
	8.22. ∑	(		)n2			.
						n
	n=1		n			5
	∞	1
	8.23. ∑					.
		3 4(n − 1)
	n=1

∞n!

8.24.∑n=1 5n (2n + 1) .

∞

2n + 1

n

1

8.25. ∑

(

)

.

2

n

n

n=1

3

− 1

n

∞

(2n + 1)!

8.26. ∑

.

n 2

n=1

3

n

∞

2n − 1

8.27. ∑

(

)2n+1 .

n=1

3n + 1

∞

n

+ 1

8.28. ∑

.

n

n=1

2

n!

∞3n nn

8.29.∑n=1 (2n + 1)n .

8.30.∑∞ 3n −n 1 .

n=1 4 2

№№ 9.1-9.30. Вычислите определенный интеграл с точностью до 0,001, разлагая подынтегральную функцию в ряд и затем интегрируя его почленно.

0,5

9.1. ∫ x e− x dx .

0

0,5sin x

9.2. ∫ dx .

0 x

0,5

9.3. ∫ x cos xdx .

0

0,5

9.4. ∫ xe− x dx .

0

0,1 e x − 1

9.5. ∫ dx .

0 x

9.6. ∫	1 − cos x					dx .
		x		2
0
9.7. ∫1	cos				xdx .
0
9.8. ∫1	e−	x 2	dx .
		3
0

9.9. ∫1 x sin xdx .

0

	1
9.11. ∫ sin x dx .
	0			x
	1			dx .
9.12. ∫
	0 1			+		x
	0,25
9.13.	∫			xe−2 x dx .
	0
9.14. ∫1			cos x					dx .
			2
	0			x
	0,5			dx
9.15. ∫										.
								4
	0 1 + x
	0,5
9.16. ∫		ln(1 + x2 )									dx .
	0					x
	1 sin x						2
9.17. ∫										dx .9.18.
				x	2
	0
0,25
∫ cos x dx .
0	x
	0,5
9.19. ∫ ln(1 + x) dx .
	0							x

	1			cos x							2
9.21. ∫													dx .
						x	2
	0
	1			sin				1		x
							2
9.22. ∫													dx .
						x
	0
	0,2						1
9.23. ∫													dx .
				1 +			3				x
	0
	0,5
9.24. ∫					ln(1 + x3 )									dx .
	0								x
	0,5										x dx .
9.25. ∫ sin
	0						x
	0,3				1 x
9.26. ∫ e 2								dx .9.27.
	0					x
0,5ln(1 +				1		x)
				2
∫									dx .
	x
0
	0,1						dx						.
9.28. ∫
	0 1 +							1					x
							2

14

0,5	0,5	− cos x dx .	9.29.	0,5
9.10. ∫ e− 2 x2 dx .	9.20. ∫1			∫ x e− x dx .
0	0	x		0
				0,25
			9.30.	∫ 4 x cos 4 xdx .
				0

Образцы решений заданий контрольной работы № 3

Пример. Найти частные производные следующих функций:

1)z = x3 + 3y2 x5 − 4x2 y4 + 3x − 4 y + 1;

2)z = e xy ;

3)z = ln(4x2 − 5y) .

1) Пусть z = x3 + 3y2 x5 − 4x2 y4 + 3x − 4 y + 1.

Считая переменную y константой, найдем

∂z = 3x2 + 3y2 5x4 − 4y4 2x + 3.

∂x

Считая константой переменную x , получим:

∂ z	= 3x5 2 y − 4x2 4 y3 − 4 .
∂ y

2) Пусть z = e xy . Тогда

∂z = exy (xy)x′ = exy y,

∂x

∂ z

= exy (xy) y′ = exy x .

∂

y

3) Пусть z = ln(4x2 − 5y) . Тогда

∂

z

=

8x

;

∂

x

4x 2

− 5y

∂

z

=

− 5

;

∂

y

4x2 −

5y

∂

2

z

∂ z

′

8(4x 2

− 5y) − 8x 8x

32x 2

+ 40 y

=

x

=

= −

∂

x 2

∂ x

(4x 2 − 5y)2

(4x 2 − 5y)2

∂ 2 z

∂ z ′

0 − 8x (−5)

40x

=

y =

=

∂ x∂

y

∂

x

(4x 2 − 5y)2

(4x 2 − 5y)2

∂

2

z

∂ z

′

0 − (−5)(−5)

25

=

y =

= −

∂

y

2

∂

y

(4x

− 5y)

(4x

− 5y)

2

2

2

2

∂ 2 z

∂ z

′

0 − (−5) 8x

40x

=

x =

=

2

2

2

2

∂ y∂

x

∂

(4x

(4x

y

− 5y)

− 5y)

Убеждаемся, что

∂ 2

z

=

∂ 2 z

∂

x∂

y

∂

y∂

x

Пример. Дана функция

z = x2 − 5x3 y2 + 4x − 8y + 3 , точка М0(2, –3) и вектор

= 3i + 4

.

Найти

z

в точке М0

и производную по направлению вектора s в

s

j

grad

этой же точке.

15

∂ z

∂ z

′

′

Имеем grad z =

i +

(x0

(x0 , y0 ) j .

∂

x

∂

y

j = f x

, y0 )i + f y

Находим

∂z = 2x − 5y2 3x2 + 4 ;

∂x

∂	z			=	∂	z	(2,−3) = 2 2 − 5(−3)2	3 22	+ 4 = −532 ;
∂	x		М0		∂	x

∂z = 0 − 5x3 2y − 8;

∂y

∂ z

= ∂ z

(2,−3) = −5 23 2(−3) − 8 = 232 .

∂ y

М0

∂ y

Следовательно

grad

z = −532i

+ 232 j .

Далее,

∂ z =

∂ z cosα + ∂ z cos β

– производная по направлению вектора s

в

∂ s

∂ x

∂ y

точке М0.

∂ z

= −532;

∂ z

= 232.

∂ x

∂ y

М0

М0

sy

Находим cosα =

s

x

; cos β =

.

Имеем:

s

s

32 + 42 = 5 . Значит,

cosα =

3

; cos β =

4 .

sx

= 3; s y

= 4;

s =

∂ z

= −532 3

+ 232 4

5

5

Поэтому

= 133,6.

∂ s

5

5

Пример. Требуется изготовить закрытый цилиндрический бак данного объема V. Стоимость квадратного метра материала, идущего на изготовление стенки бака равна 8 рублей, а на изготовление дна и крышки – 6 руб. Определить размеры бака так, чтобы затраты на покупку материала, идущего на его изготовление, были наименьшими.

Решение. Площадь полной поверхности бака равна S = Sбок.+Sосн.= 2π r h + 2π r2. Объем бака равен V=π r2h, где r и h – радиус основания и высота бака соответственно. Стоимость материала, идущего на изготовление бака будет u(r, h)=2π rh 8+2π r2 6 (руб.). Нужно найти min этой функции, при условии, что

πr2 h=V или πr2h – V=0. Составим функцию:

F(r, h) = 2π rh 8+2πr2 6+λ(π r2h – V).

Найдем ее производные по переменным r, h, λ и приравняем их к нулю.

	∂F	= 16π h + 12π 2r + λπ h 2r = 0
	∂r
	∂F
		= 16π		r + 0 + λ π r	2	= 0
	∂h
	∂F	= π r	2	h − V = 0
	∂λ

16

Из второго уравнения системы (при

r ≠ 0 )

находим

16π + λπr = 0 ,

откуда

λr = −16 , тогда из первого уравнения получим 16πh + 24πr − 32πh = 0

или 2h = 3r ,

т.

е.

h =

3r

.

Подставляем

это

значение

в

третье

уравнение

3r = V

2

2V ; r = 3

2V ед.

πr 2

; r 3 =

длины

масштаба

и

тогда

2

3π

3π

h = 3 r = 3 3

2V = 3

2 27 V =

3 9V ед. длины масштаба.

2

2

3π

3 8π

4π

Из экономического смысла задачи следует, что min функции u(r, h) существует, и будет определяться найденными значениями r и h. Очевидно также

umin = 2π

3

2V

3

9V

8 + 2π 3

4V 2

6

или

umin = 16π 3

3V 2

+ 12π 3

4V 2

(руб.)

3π

4π

9π 2

2π 2

9π 2

Пример.

Экспериментально получены

пять значений искомой функции

y = f (x) при пяти значениях аргумента, которые записаны в таблице:

xi

1

2

3

4

5

yi

0,5

1

1,5

2

3

Методом наименьших квадратов найти искомую функциональную

зависимость в виде

y = kx + b . Экспериментальные точки и полученную прямую

изобразить в системе координат XOY.

Запишем систему уравнений для нахождения коэффициентов k и b.

	n	n	n
k ∑ xi 2		+ b ∑ xi = ∑ xi yi
	i=1	i=1	i=1	.
	n	n
k ∑ xi + bn = ∑ yi
	i=1	i=1
Учитывая, что n = 5 и значения xi и yi известны, находим
5
∑ xi = 1+ 2 + 3 + 4 + 5 = 15;
i=1
5
∑ xi 2 = 12 + 22 + 32 + 42 + 52 = 55 ;
i=1
5
∑ yi = 0,5 + 1 +1,5 + 2 + 3 = 8 ;
i=1
5
∑ xi yi = 1 0,5 + 2 1 + 3 1,5 + 4 2 + 5 3 = 30
i=1
Получаем
k 55 + b 15 = 30				11 k + 3b = 6	, откуда k = 0,6 и b = −0,2 .
		5 = 8	или	15k + 5b = 8
k 15 + b

17

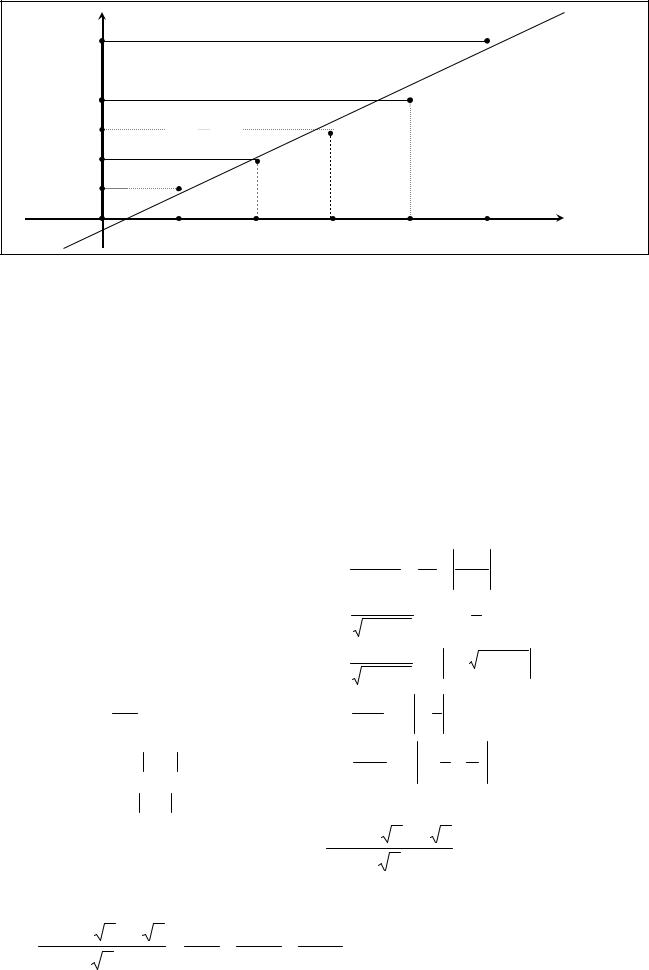
Таким образом, наилучшее приближение к искомой зависимости в линейной
форме имеет вид y = 0,6x − 0,2 (см. рис.).
y					y=0,6–0,2
3
2
1,5
1
0,5
0	1	2	3	4	5	х

Методические указания и образцы решений заданий контрольной работы № 4

Интегральное исчисление

Таблица основных формул интегрирования:

1. ∫du = u + C ;

10. ∫

du

= tg u + C ;

cos

2

u

uα +1

2. ∫u

α

du

=

+ C, гдеα ≠ −1 ;

11. ∫

du

= − ctg u + C ;

α + 1

sin

2

u

3. ∫ u −1 du = ∫

1

du = ln

u

+ C ;

12 . ∫

du

=

1

arctg

u

+ C ;

2

2

u

a

+ u

a

a

4. ∫cosu du = sin u + C ;

13. ∫

a

2 du

2

=

1 ln a + u

+ C;

− u

2a

a − u

5. ∫sin u du = − cosu + C ;

14. ∫

du

= arcsin

u

+ C ;

a

2

− u

2

a

6. ∫e

u

du = e

u

+ C ;

15. ∫

du

= ln u +

u

2

± a

2

+ C ;

u

2

± a

2

7. ∫au du =

au + C ;

16. ∫

du

= ln tg u

+ C ;

ln a

sin u

2

8. ∫ tg udu = − ln cosu + C ;

du

u

π

17. ∫ cosu

= ln tg

2 +

4

+ C .

9. ∫ctg udu = ln sin u + C ;

Пример. Вычислить интеграл: I = ∫ 4x2 − 3

x + 23 x dx

3 x

Преобразуем подынтегральное выражение

4x2 − 3 x + 23 x

4x2

3x1/ 2

2x1/ 3

3

x

=

1/ 3 −

1/ 3

+

1/ 3 = 4x5 / 3 − 3x1/ 6 + 2 . Следовательно,

x

x

x

18

I = ∫			(4x5 / 3 − 3x1 / 6 + 2)dx = 4∫ x5 / 3dx − 3∫ x1 / 6dx +2∫ dx =4																	x8 / 3	− 3 x7 / 6	+ 2x + C =
																			8 3		7 6
=	3	3	x	8	−	18 6	x	7	+ 2x + C =	3	x	2 3	x	2	−	18 6	x	7	+ 2x + C.
	2					7				2						7

Здесь мы воспользовались свойствами неопределенного интеграла и формулами 2 и 1 таблицы интегралов. Сделаем проверку правильности интегрирования. Найдем I ′ .

	3	x8 / 3		18		x7 / 6	′		3		8		x5 / 3		18			7	x1/ 6	+ 2 + 0 = 4x5 / 3 − 3x1/ 6 + 2,
I ′ =			−				+ 2x + C	=						−
				7					2		3				7			6
2

что совпадает с преобразованным подынтегральным выражением.

Метод подстановки

Примеры. Вычислить интегралы:

	u = cosx			u	4		4	x
							cos
1)	I = ∫cos3 xsinxdx=		= −∫u3du= −			+ C = −				+ C
				4			4
	du= −sindx

4

x

′

1

Проверка: −

cos

+ C

= −

4cos3 x (cos x)′ = − cos3 x(− sin x) = cos3 x sin

4

4

что совпадает с подынтегральным выражением.

2

= sin x

2) I = ∫

u

= ∫ u5 du = ∫u5 / 2du =

u7 + C =

sin5 x cos xdx =

7

du = cos xdx

= 2 u3

u + C =

2 sin3 x sin x + C .

7

7

Проверка:

2

′

2

′

=

2

7

sin5 / 2

x (sin x)′ = sin5 / 2

x cos x = sin5

7

sin3 x sin x + C =

sin7 / 2 x + C

7

2

7

что и требовалось доказать.

x3

3

u du

1

3) I = ∫e

x

2

u = x

∫e

∫e

u

dx =

2

2

du

=

=

du =

3

3

du

=

3x

dx, x

dx =

3

= 1 eu + C =

1 ex3

+ C .

3

3

′

(

3 )′

Проверка:

1

x3

1

x3

1

x3

2

x3

2

—

это

и

e

+ C

=

e

=

e

3x

= e

x

3

3

x

3

x ,

x cos x,

есть

подынтегральное выражение.

u = kx

du

1

1

1

4) I = ∫ cos kx dx =

= ∫ cosu

=

∫ cos u du =

sin u + C =

sin kx + C .

k

k

k

k

du = kdx

1

Аналогично находится: ∫sin kxdx = −

cos kx + C .

k

19

Замечание. В некоторых случаях подстановку удобнее сделать в виде

x = ω (u). Например, (вывод формулы 12 из таблицы интегралов) I = ∫							dx		.
					a	2	+ x	2
1
Возьмем x = a tgu , тогда dx = a		du . Найдем
	cos2 u
a2 + x2 = a2 + a2 tg2 u = a2 (1+ tg2 u) = a2			1	.
			cos2 u

Перейдем под интегралом к новой переменной u . Получим:

a

1

du

I = ∫

cos2 u

= ∫ 1 du =

1

∫ du = 1 u + C .

a2

1

a

a

a

cos2 u

x

x

Если

x = a tg u, то

tg u =

и

u = arctg

. Заменяя

в

правой части

a

a

dx

1

x

переменную u ее значением получим окончательно: I = ∫

=

arctg

+ C.

a2 + x2

a

a

Метод интегрирования по частям

Пусть u(x) и v(x) – две дифференцируемые в некоторой области функции. Тогда справедлива следующая формула:

∫ udv = uv − ∫ vdu ,

(1)

которая называется формулой интегрирования по частям и которая позволяет вычислить один из двух симметричных по форме интегралов, через другой.

Пример. Вычислить: I = ∫ x cos 83 xdx .

Все необходимые вычисления будем проводить одновременно с применением приведенной выше формулы (1)

						3			u = x,						du=dx
	I =	∫ x cos					xdx = dv = cos					3		xdx,v = ∫ cos					3		xdx =			8	sin	3	x	=
						8
												8
																		8						3		8
	= x	8	sin	3	x − ∫			8	sin	3	xdx =		8		xsin	3	x +	64		cos		3	x + C.
				8						8						8		9				8
		3						3				3

Здесь мы, кроме формулы (1), использовали уже разобранные примеры для вычисления интегралов от coskx и sin kx .

Интегрирование рациональных дробей

1. Вычислить интеграл: J = ∫	(4x + 2)dx	.
	x(x − 1)(x + 2)

Разложим подынтегральную дробь на простейшие дроби по схеме:

1	=	A		+	B	+	C		.
x(x −1)(x + 2)		x			x −1		x +	2

20