2484

Приведем дроби в правой части к общему знаменателю. Тогда:

4x + 2

=

A(x − 1)(x + 2) + Bx(x + 2) + Cx(x − 1)

, откуда

x(x − 1)(x + 2)

x(x − 1)(x + 2)

4x + 2 ≡ A(x – 1)(x + 2) + Bx(x + 2) + Cx(x – 1)

при x = 0

2 = –2A,

A = –1

при x = 1

6 = 3B,

B = 2

при x= –2 –6 = 6C,

C = –1

− 1

2

1

Итак J = ∫

+

−

dx

= − ln

x

+ 2 ln

x − 1

− ln

x + 2

+ C

x

x −

1

x + 2

(x + 15)dx

2. Вычислить интеграл: J

= ∫

.

(x − 3)(x2 +

9)

Разложим подынтегральную дробь на простейшие дроби:

x + 15

=

A

+

Bx + C

=

Ax2 + 9A + Bx2 + Cx − 3Bx − 3C

.

(x − 3)(x2

+ 9)

x −

3

x2

+ 9

(x − 3)(x2

+ 9)

Следовательно х + 15 ≡ (А + В)х2 + (С – 3В)х + 9А – 3С.

Сравним коэффициенты при одинаковых степенях х в левой и правой частях:

x2

A + B = 0

A = −B

A = −B

x

C − 3B = 1

3C + 9A = 3 18A = 18 A = 1; B = −1; C = −2.

C + 3a = 1

0

9A − 3C = 15

9a − 3c = 15

+

x

9A − 3C = 15

Итак:

ln(x

+ 9)− 2

1

− x

− 2

dx

xdx

dx

1

2

1

x

J =

+

dx =

−

− 2

= ln

x − 3

−

arctg

+ c

∫ x − 3

x2 + 9

∫ x −

3

∫ x2 +

9

∫ x

2 + 9

2

3

3

.

Определенный интеграл

Определенные интегралы вычисляются по формуле Ньютона-Лейбница

b

∫ f (x)dx = F (x) ba = F (b) − F (a) ,

a

где F(x) одна из первообразных функций для функции f(x). Например,

1	2		x3			1		1		0		1
I = ∫ x		dx =				0	=		−		=		;
			3					3		3		3
0

π
2	π	2
I = ∫cos xdx = sin x
	0
0

= sin π2 − sin 0 = 1− 0 = 1.

Если для вычисления определенного интеграла требуется сделать подстановку u=ϕ(x) или x=ϕ(u), то перейдя под интегралом к новой переменной u, найдем пределы изменения этой переменной и вычисляем новый интеграл с новыми

b	β	α и	β определяются из уравнений
	′
пределами: I = ∫ f (x)dx = ∫ f (ϕ (u))ϕ (u)du , где
a	α

ϕ(α)=a; ϕ(β)=b.

21

Примеры.

			10							u = 3 x + 6 ;						если		x = 1,				то u = 9					36		du
1) I =			∫	3 x + 6 dx					=			= 3 dx		;		если	x = 10 ,					то u =		36		=	∫	u		=
			1							du																	9		3
			1				3
	1	36			1 u 2				36		2		3 36		2		36			2		36 6 −	2	9 3 =
=		∫ u 2 du		=		3			9	=	9	u	9	=	9	u u	9		=	9			9
	3				3
		9
= 48 − 6 = 42 .						2
			π								π									π

			2		3 x sin
2 ) I =			∫ cos
		0
	u = sin x ;
=
		= cos			xdx ;
	du

11

=∫ u 2 du − ∫ u 4 du

00

2 xdx			2					2 x sin 2													2			− sin 2 x ) sin 2 x cos xdx =
		=	∫ cos										x cos xdx						=		∫ (1
			0																		0
	если			x = 0 , то									u = sin				0 = 0							=	1	− u 2 ) u 2 du	=
								π										π							∫ (1
			x =									то		u = sin
	если							2		,								2	= 1						0
	u 3		u 5				1				1		1		2
		1
=		0 −					0	=				−		=			.
	3		5								3		5		15

Несобственные интегралы

Несобственные интегралы по бесконечному промежутку.

Пусть функция y = f(x) определена и непрерывна при а ≤ х < ∞. По определению:

∞		N
∫ f (x)dx = lim		∫ f (x)dx , называется несобственным интегралом.
a	N →∞ a

Если предел справа равен конечному числу, то несобственный интеграл наывается сходящимся. Если предел равен бесконечности или не существует вообще, то несобственный интеграл называется расходящимся.

Примеры.

∞

dx

1

N

d(5x − 3)

1

0N ) =

1

lim (ln(5N − 3) − ln 3) = ∞ .

1) ∫

= lim

∫

=

lim (ln

5x − 3

5x − 3

5x − 3

0

N →∞

5

0

5 N →∞

5

N →∞

Это значит, что несобственный интеграл расходится.

∞

dx

1

N

d(4 − 7x)

1

(4

− 7x)

− 4

1N =

2) ∫

=

lim

−

∫

= −

lim

1 (4 − 7x)5

N →∞

7

0

(4 − 7x)5

7

N →∞

− 4

1

(4 −

7x)

− 4

N

1

1

1

lim

lim

= −

1 = −

−

+

=

7

− 4

7

4(4 − 7N)

4

4(4 − 7 1)

4

N →∞

N →∞

1

1

1

= −

0 +

= −

.

7

4

34

2258

Таким образом, данный несобственный интеграл сходится.

22

Дифференциальные уравнения

1. Дифференциальные уравнения с разделяющимися переменными.

Эти уравнения можно представить в виде:

y/ = f1(x) f2(y) или P1(x)Q1(y)dx+P2(x)Q2(y)dy = 0.

Решения этих уравнений поясним на примерах.

Пусть y/ = ycosx; тогда dydx = y cos x , dy=y сosx dx; dyy = cos x dx . Интегрируя

обе части полученного равенства, найдем ln y =sinx+c, откуда y = esinx+c – общее решение данного уравнения.

Рассмотрим уравнение x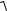 1− y2 dx = − y 1+ x2 dy .

Разделим обе части полученного уравнения на 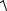1 − y 2 1 + x 2 .

Получим:	xdx	= −	ydy .
	1 + x2		1 − y2

Переменные х и у разделились в этом равенстве. Интегрируя его,

найдем: ∫

xdx

= −∫

ydy

+ C .

1 + x2

1 − y2

Вычислим первый интеграл ∫

xdx

:

1 + x2

du

Пусть 1 + x2 = u, тогда du = 2xdx, xdx =

2

du

= 1 ∫u−

1

1

xdx

= 1 ∫

du

1 u 2

∫

= ∫ 2

1 + x2

+ C .

2 du =

+ C =

u + C =

2

u

2 1

1 + x

u

2

2

2

ydy

Второй интеграл вычисляется аналогично: − ∫

=

1 − y 2

+ C .

1 − y 2

Следовательно,

1+ x2 =

1− y2 + C – это общий интеграл данного уравнения.

Выражая из общего интеграла функцию у, можно найти общее решение дифференциального уравнения.

2. Однородные дифференциальные уравнения первого порядка.

Уравнение первого порядка y′ = f (x, y) называется однородным, если f(x, y) является однородной функцией нулевого порядка, т. е. f(tx,ty) = t0f(x,y)= f(x,y).

Подстановкой xy = u , или y = u x , это уравнение сводится к уравнению с

разделяющимися переменными.

Пример. Найти общее решение уравнения xy y′ = x2 + y2 .

23

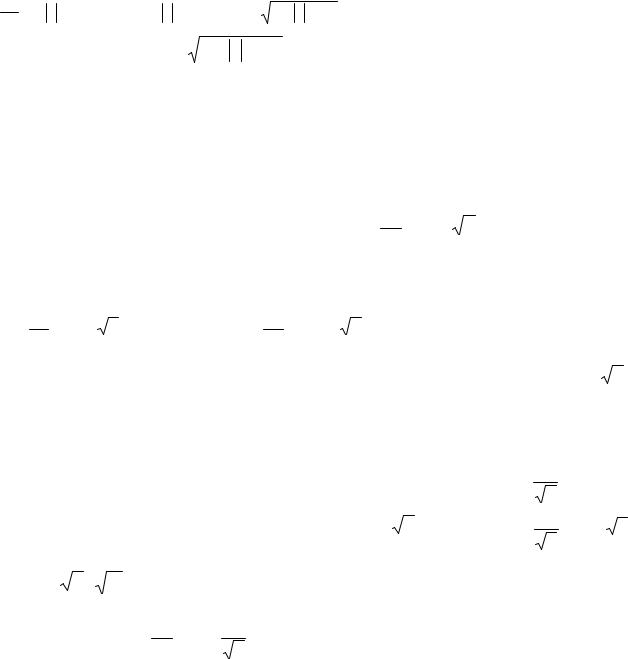
Находим y

′

=

x2

+ y2

, y

′

x2

y 2

y

′

x y

xy

= xy

+ xy ;

= y

+ x

. Делаем подстановку:

y

= u;

y = ux;

y

′

′

′

. Тогда

x

= u x + ux

′

1

′

1

du

1

dx

u x + u =

+ u; u x =

;

x =

; udu =

.

u

u

dx

u

x

Интегрируя, получим

u 2

= ln x + C; u 2 = 2 ln x + C ; u = ± 2 ln x + C .

2

1

1

Следовательно y = ± x

2 ln x + C1

– общее решение данного уравнения.

3. Линейные дифференциальные уравнения.

Уравнение вида:

y′ + P(x) y = Q(x), где P(x) и Q(x), непрерывные в некоторой

области функции, называется линейным. Это уравнение сводится к уравнению с разделяющимися переменными подстановкой y = uv , действие которой покажем на

примере.

Пример. Найти общее решение уравнения y′ +	y	= x2	x .
	2x

Делаем подстановку y = uv , где u и v неизвестные пока функции аргумента х. Находим y′ = u′v + v′u и подставляем значения y и y′ в данное уравнение

u′v + v′u + uv

= x2

x

или

u′v + u v′

+ v = x2

x . Выберем функцию v(x)

так,

2x

2x

чтобы v′ +

v

. Тогда

′

v = x

2

x .

2x = 0

функция u будет находиться из уравнения u

Таким образом, нахождение неизвестной

функции y(x) сводится

к

последовательному нахождению функций v(x) и u(x)

из указанных уравнений:

v

dv

v

dv

dx

1

1

1 .

v′ +

= 0;

= −

;

= −

;

ln

v

= −

ln

x

;

v = x−

=

2

2x

dx

2x

v

2x

2

x

′

v

= x

2

x . Получим u′

1

2

Подставим это значение в уравнение

u

x = x

x

или u

′

= x

2

x

x,

u

′

= x

3

. Интегрируя

x4

это

равенство

найдем u

= 4 + C

и

4

1

окончательно, y = u v = x

+ C

— общее решение данного уравнения.

4

x

Дифференциальные уравнения второго порядка

Наиболее важными для практики являются линейные уравнения второго порядка.

Эти уравнения имеют вид ay′′ + by′ + cy = f (x) .

Общим решением этого уравнения будет

24

y = y + y ,
где y – общее решение соответствующего уравнения	без правой части
(однородного): ay′′ + by′ + cy = 0 , а y* – некоторое частное	решение исходного

уравнения.

Будем рассматривать наиболее часто встречающиеся в практике случаи, когда коэффициенты a,b, c являются постоянными числами, а правая часть имеет простой (специальный) вид. Для нахождения y составляется характеристическое уравнение

ak 2 + bk + c = 0 , находятся его корни k1 и k2 и, в зависимости от их значений, определяется y .

Правило нахождения y укажем в таблице № 1:

Характеристическое уравнение: ak 2 + bk + c = 0 Дискриминант: D = b2 − 4ac

1.D > 0, k1 ≠ k2 – действительные и различные: y = c1ek1x + c2ek2 x

2.D = 0, k1 = k2 – действительные и равные: y = (c1 + c2 x)ek1x

3.D < 0, k1 = α + βi, k2 = α − βi – комплексно сопряженные: y =eαx(c1cosβ x+c2sinβ x)

Частное решение y* находится по правилу, указанному в таблице № 2:

f(x)

f(x)=Pn(x)

f(x)=Pn(x)eαx

f(x)=a0cosβx+b0sinβx

y*

1.y*=Qn(x), если среди корней характеристического уравнения нет числа 0.

2.y*=Qn(x) x, если число 0 является однократным корнем характеристического уравнения.

3.y*=Qn(x) x2, если число 0 является двукратным корнем характеристического уравнения.

4.y*=Qn(x) eαx, если среди корней характеристического уравнения нет числа α.

5.y*=Qn(x) eαx х, если α является однократным корнем характеристического уравнения.

6.y*=Qn(x) eαx х2, если α является двукратным корнем характеристического уравнения.

7.y*=Aсosβx+Bsinβx, если число βi, где i = − 1–

мнимая единица, не является корнем характеристического уравнения.

8.y*=(Acosβx+Bsinβx)х, если число βi является корнем характеристического уравнения.

В этой таблице Qn(x)=A0xn+ A1xn-1+…+ An многочлен той же степени, что и Pn(x), но с неизвестными коэффициэнтами, которые и нужно найти.

25

Примеры.

1.Найти общее решение уравнения у// – 5у/=х.

Обозначим искомое решение через у. Тогда у= у+у*, где у – общее решение уравнения у// – 5у/=0. Составим характеристическое уравнение: k2–5k=0; k(k–5)=0; k1=0; k2=5. Следовательно у=с1е0х+с2е5х=с1+с2е5х. Найдем теперь у*. Так как правая часть уравнения равна f(x)=1 х+0, то частное решение у* было бы: у*=Ах+В, если бы числа 0 не было среди корней характеристического уравнения. Но в нашем случае 0

встречается среди корней характеристического уравнения один раз.Это случай 2, табл. № 2 . Поэтому у*=(Ах+В)х=Ах2+Вх. Найдем (у*)/=2Ах+В; (у*)//=2А, подставим

эти значения в данное уравнение и потребуем, чтобы оно обратилось в тождество: 2А-5(2Ах+В)≡1 х+0; -10Ах+2А-5В≡1 х+0, откуда

− 10А = 1			1			2	А		2			1			1	.
	А− 5В = 0	А = −			; В =			=			−			= −
			10			5			5						25
2												10

Таким образом, y* = 101 x2 − 251 x и общее решение уравнения будет

y = y + y* = c1 + c2e5x − 101 x2 − 251 x .

2. Найти общее решение уравнения у//+4у/+13у=2cos4x

Обозначим искомое решение через у. Тогда у= у+у*, где у — общее решение уравнения у//+4у/+13у=0. Составим характеристическое уравнение k2+4k+13=0. Решая это уравнения находим корни: k1 = –2 + 3i; k2 = –2 – 3i. Следовательно у=е-2х(C1cos3x+C2sin3x). Найдем теперь у*.Т.к. β=4i нет среди корней характеристического уравнения (случай 7 табл. 2), то частное решение у* подбираем в виде у*=Acos4x+Bsin4x; (у*) /= –4Asin4x + 4Bcos4x; (у*)// = –16Acos4x – 16Bsin4x.

Подставляем эти значения в уравнение, приводим подобные слагаемые, получаем: cos4x(16B-3A)+sin4x(-16A-3B)=2cos4x. Приравнивая коэффициэнты при sin4x и cos4x находим:

16B − 3A = 2

− 16A − 3B = 0

	Решая систему получаем A = −	6		; B =		32
		265
				265
	Частное решение имеет вид y*	= −		6	cos 4x +			32	sin 4x
								265
		265								6					32
	Общее решение уравнения y = e-2x (C1 cos3x + C2 sin 3x) −											cos 4x +				sin 4x
										265
														265
	3. Найти частное решение уравнения у//+4у/+4у=3е2х, удовлетворяющее
	начальным условиям у(0) = 1, у/(0) = 2.
	Найдем сначала общее решение данного уравнения у= у+у*.
	у//+4у/+4у=0; k2+4k+4=0;	D=16–16=0;						k1,2 =			− 4 ± 0		;	k1 = −2; k2 = −2.
										2

Следовательно, у=с1е-2х+с2е-2хх. Так как числа α=2 нет среди корней характеристического уравнения (случай 4 табл. № 2), то частное решение у* подбираем в таком же виде, как и правая часть у*=Ае2х; (у*)/=Ае2х 2; (у*)//=Ае2х 4. Подставляем эти значения в уравнение 4Ае2х+4 2Ае2х+4Ае2х=3е2х; 16Ае2х=3е2х;

16А=3; А= 3 . Следовательно, у*= 3 е2х. Значит, у= у+у*= =с1е-2х+с2е-2хх+3/16е2х –
16	16

26

общее решение данного уравнения. Для нахождения частного решения, удовлетворяющего заданным начальным условиям, найдем ещё

у/=с1е-2х(–2)+с2(е-2х(–2)х+е-2х 1)+3/16 е2х 2. Так как у(0)=1 и у/(0)=2, то получим

y(0) = 1 = c e−2 0

+ c

e−2 0

0 +

3

e2 0

c

+

3

= 1

13

13

16

16

1

2

1

.

3

3

; c1

=

; c2

=

16

4

y′(0)

=

2 = −2c e−2 0

+ c

2

(0 + 1) +

e0

− 2c + c

2

+

= 2

1

8

1

8

Подставляя

эти

значения

в

общее

решение,

найдем

окончательно

y =

13

e

− 2 x

+

13

e

− 2 x

x

+

3

e

2 x . Это

есть

частное

решение

данного уравнения,

16

4

16

удовлетворяющее данным начальным условиям.

	Ряды
Рассмотримбесконечнуюпоследовательностьдействительныхчисел а1, а2, …,аn,...
Выражение вида
а1+ а2+ а3+ ... аn+...	(2)
называется числовым рядом.

Рассмотрим Sn= а1+ а2+ а3+ ... аn – n-ю частичную сумму ряда (2)

Если lim Sn = S , где S – действительное число, то это число называется суммой

n→∞

ряда (2) ,а сам этот ряд называется сходящимся. Если же S = ∞ или не существует вообще, то ряд суммы не имеет и называется расходящимся.

Для рядов с положительными членами справедливы достаточные признаки

сходимости.
Признак сравнения.
Пусть даны два ряда
а1+ а2+ а3+ ... аn+...	(3)
b1+ b2+ b3+ ... bn+...	(4)

причем an ≤ bn (n=1, 2, 3,...). Тогда из сходимости ряда (4) следует сходимость ряда (3). Из расходимости ряда (3) следует расходимость ряда (4).

Предельный признак сравнения: если существует конечный и отличный от

нуля предел lim	an	= k , то оба	ряда	(3) и (4)		одновременно сходятся или
	b
n→∞ n
одновременно расходятся.
Признак Даламбера.				an+1
Если для ряда (2) существует			lim		= l , то этот ряд сходится при l<1 и
расходится при l>1.			n→∞	an
Признак Коши.						то ряд сходится при l<1 и
Если для ряда (2) существует lim n an = l ,
расходится при l>1.			n→∞

27

Интегральный признак.

Если f(x) при х≥1 непрерывная, положительная, монотонно убывающая функция, причем f(n)=an (n=1,2,...), то ряд (2) сходится или расходится в

		∞
зависимости от того, сходится или расходится несобственный интеграл		∫ f (x)dx .
Для знакочередующихся рядов вида		1
а1 – а2+ а3 – ...+...(–1)n+1аn+...,	(5)

где an≥0, справедлив признак Лейбница:

Если абсолютные величины членов ряда (5) монотонно убывают, а общий член ряда стремится к нулю, т. е., если выполняются условия:

1) а1>а2> а3>..> аn> ... и 2) lim an = 0,

n→∞

то ряд (5) сходится.

Можно доказать, что сумма сходящегося знакочередующегося ряда (5) не превосходит абсолютной величины первого члена этого ряда.

Примеры.

∞

1)4n

(2n +

1. Исследовать на сходимость ряд: ∑

.

n=1

n!

Имеем an =

(2n + 1)4n

,

an+1

=

(2n + 3)4n+1

.

По признаку Даламбера находим

предел:

n!

(n + 1)!

l = lim

a

n+1

=

lim

(2n + 3)4 n+1 n!

= lim

4(2n + 3)

= 4 lim

2n + 3

=

n→∞

an

n→∞ (n +1)!(2n +1)4 n

n→∞ (n +1)(2n +1)

n→∞ 2n2 + 3n

+1

2

+

3

= 4 lim

n

n2

= 4

0

= 0,

т. к. l<1, то ряд сходится.

3

2

n→∞ 2 +

+

1

n

n2

∞

n+1 4n + 1 n

2. Исследовать на сходимость ряд ∑2

.

n=1

7n − 3

Применим признак Коши. Найдем

n

n

n+1

4n + 1 n

n+1

4n + 1

l = lim

a

= lim n 2

= lim 2

n

=

n→∞

n→∞

7n − 3

n→∞

7n − 3

Следовательно, данный ряд расходится.
	∞	cos 2		n	.
3. Исследовать на сходимость ряд ∑			n n
	n = 1
Сравним этот ряд с рядом
∞	1
∑
n=1n	n

			4 +		1
1									4		8
lim 21+	n				n			= 2		=		> 1.
									7		7
n→∞			7 −		3
					n

(6)

28

Имеем,

cos2 n

≤

1

.

n n

n n

Применяя интегральный признак, вычисляем интеграл.

1

n

∞ dx

n dx

x−

1 n

1

= lim

= lim

2

= − 2 lim

= 2.

I = ∫

∫

1

= −2 lim

− 1

1 x x

n→∞

1 x x

n→∞

−

n→∞

x 1

n→∞ n

2 1

Это значит, что интеграл сходится, а, значит, и ряд (6) также сходится. Тогда по признаку сравнения сходится и исходный ряд.

Приложения степенных рядов.

Если функция f (x) имеет производные любого порядка в интервале |х–х0|< r, где r≥0, то в этом интервале она может быть разложена в сходящийся ряд Тейлора.

f (x) = f (x ) + f ′(x ) (x − x ) +			f ′′(x )	(x − x )2	+	f (n) (x )	(x − x )n +
			0			0
0	0	0	2!	0		n!	0

При х0=0 получается ряд Маклорена:

	f (x) = f (0) + f ′(0)x +	f ′′(0)	x2	+	f (n) (0)	xn +
		2!			n!

Приведём разложения в ряды Маклорена и соответствующие области сходимости соответствующих рядов, для наиболее часто встречающихся в практике функций

ex = 1+ x +

x2

+

x3

+ ...+

xn

+ ...;

x (−∞, ∞) .

n!

2!

3!

x2n−1

sin x = x −

x3

+

x5

− ... + (−1)n−1

+ ...;

x (−∞, ∞) .

(2n − 1)!

3!

5!

cosx = 1−

x2

+

x4

−...+ (−1)n−1

x2n−2

+ ...;

x (−∞, ∞) .

(2n − 2)!

2!

4!

(1+ x)α = 1+αx + α(α −1) x2

+...+

α(α −1)...(α − n+1) xn +...; x (−1;1) .

2!

n!

ln(1+ x) = x −

x2

+

x3

−

x4

+ ... + (−1)n−1

xn

+ ...;

x (−1;1] .

2

3

4

n

Пользуясь разложениями функций в степенные ряды можно вычислять приближенные значения функций в некоторых точках, вычислять определенные интегралы, находить частные решения дифференциальных уравнений.

		0,5	−	x2
	Пример. Вычислить	∫ e		2	dx с точностью до 0,001.
		0					x2
						−
	Первообразная для	функции					2 не выражается через элементарные
						e

функции. Поэтому точное значение интеграла вычислить мы не сможем. Но с помощью рядов Маклорена и действий над ними можно вычислить данный интеграл с любой степенью точности. Для этого воспользуемся известным разложением в ряд:

et = 1+ t +	t 2	+	t 3	+ ...+	t n	+ ... .
					n!
2!		3!

29

Ряд, стоящий справа равномерно сходится к функции et при любом

действительном t. Заменим t на − x2 . Получим

2

e−

x2

= 1−

x

2

+

1 x

4

−

1 x

6

+ ... .

2

2!

4

3!

8

2

Это разложение также верно при любом действительном х. Проинтегрируем последнее равенство в пределах от 0 до 0,5.

0,5					x2	0,5						2													3	5				7			0,5
∫			−								x				1					1				x			x		x
	e				2	dx =		1		−				+			x4 −					x6 + ... dx = x −				+		−			+ ...			=
								∫		2 8									48					6			40 7 48
0								0																									0
		1				1				1									1
=					−			+						−								+ ...
		2					23 6		2	5 40						2		7	7 48

Мы получили знакочередующийся ряд. Известно, что сумма знакочередующегося ряда не превосходит абсолютной величины его первого члена. Поэтому ряд, начинающийся с третьего члена, будет иметь сумму не

	превосходящую	1	=		1	< 0,001. Таким образом, если мы отбросим в правой
		25 40		1280
	части все слагаемые, начиная с третьего, то сделаем ошибку не большую 0,001.
							0,5		−	x2		1			1			23
	Итак, с точностью до 0,001 имеем: ∫e									2 dx ≈			−				=		≈ 0,47916 .
												2		2	3	6		48
							0
	Округляя до тысячных долей получим окончательно
						0,5	x2
						∫e−		dx ≈ 0,479 .
							2
						0

30