Теорема Ляпунова об устойчивости по первому приближению

Пусть поведение АС или её звена описывается системой уравнений вида (4.1). Выделим в правой части системы (4.1) её линейную часть. Это можно сделать, например, по формулам Тейлора в окрестности точки . В результате получаем систему вида:

где - матрица коэффициентов,,- члены более высокого порядка малости.

Система вида:

называется системой первого приближения для исходной системы (4.1).

Найдем корни характеристического уравнения:

(4.5)

системы (4.1), где - единичная матрица.

Теорема. 1. Если вещественные части всех корней характеристического уравнения (4.5) отрицательны, то невозмущённое движение системы (4.4)асимптотически устойчиво (сама система (4.4) асимптотически устойчива).

2. Если среди корней характеристического уравнения (4.5) имеется хотя бы один с положительной вещественной частью, то система (4.4) неустойчива.

3. Если некоторые корни характеристического уравнения (4.5) имеют нулевые вещественные части, а остальные корни имеют отрицательные вещественные части, то в случае простых (некратных) корней с нулевыми вещественными частями система (4.4) будет не асимптотически устойчива, во всех остальных случаях требуется дополнительное исследование.

Пример 1. Исследовать устойчивость нулевого решения системы

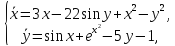
Решение. Используем теорию первого приближения. Используя разложение в ряд Тейлора в окрестности точки (ряд Маклорена):

запишем исходную систему в виде

откуда получаем систему первого приближения

характеристическое уравнение которой

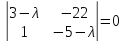
имеет корни с отрицательными вещественными частями и, следовательно, нулевое решение системы асимптотически устойчиво.

Критерий Гурвица

Теорема. Необходимым и достаточным условием асимптотической устойчивости системы (4.4) является положительность всех главных миноров матрицы размером :

,

составленной из коэффициентов характеристического уравнения (4.5), приведённого к виду:

(4.6)

Матрица Гурвица строится следующим образом. По главной диагонали выписываются коэффициенты уравнения (4.6) с 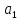по. Заполняются строки матрицы с коэффициентами уравнения (4.6) с возрастающими индексами слева направо так, чтобы строки с нечётными и чётными индексами чередовались. Если коэффициент отсутствует или индекс коэффициента меньше 0 или больше, чем, то на это место надо поставить 0.

При этом определители Гурвица имеют вид:

, ,, …,

.

Таким образом, критерий Гурвица гласит:

Для асимптотической устойчивости решения уравнения (4.4) необходимо и достаточно, чтобы выполнялись соотношения:

,, …,, при этом.

Пример 2. Исследовать на устойчивость нулевое решение уравнения

Решение. Составим характеристическое уравнение вида (4.6):

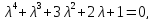
для которого ,,,,,, выполняется необходимый признак устойчивости, а матрица Гурвица имеет вид:

.

Определители Гурвица (главные миноры): ,,,, то есть согласно критерию Гурвица, нулевое решение уравнения асимптотически устойчиво.

Критерий устойчивости Михайлова

Пусть функционирование АС описывается линейным дифференциальным уравнением n-го порядка с постоянными коэффициентами:

(4.7)

Его характеристическое уравнение имеет вид (4.6). Критерий устойчивости Михайлова позволяет решить вопрос о расположении корней характеристического уравнения (4.6) на комплексной плоскости и, следовательно, решить вопрос об устойчивости нулевого решения (4.7).

Полагая , где, получаем:

где (4.8)

Величину при заданном значении параметраможно изобразить в виде вектора на комплексной плоскости. При изменении, конец этого вектора опишет некоторую кривую, которая называетсякривой Михайлова.

Теорема. Для устойчивости невозмущённого решения уравнения (4.7), характеристическое уравнение которого имеет вид (4.6) и не имеет чисто мнимых корней, необходимо и достаточно, чтобы вектор 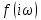, описывающий кривую Михайлова, повернулся на угол, где- степень многочлена (4.6).

Практически кривая Михайлова строится следующим образом:

1. Для уравнения -го порядка составить характеристический многочлен вида (4.6).

2. Составить характеристический комплекс , положив.

3. Найти точки пересечения кривой Михайлова с осям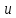и и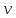, для чего надо решить уравненияи

4. Для полного представления о поведении исследуемой кривой задать промежуточные значения 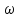, по формулам (4.8) вычислитьи, полученные значения соединить плавной кривой.

5. Найти результирующий угол поворота вектора.

6. По формуле определить значение- число корней в положительной полуплоскости и сделать вывод об устойчивости системы.

Пример 3. Исследовать на устойчивость нулевое решение уравнения по критерию Михайлова

Решение. Составляем характеристический многочлен

.

Положим ,, тогда характеристический комплекс имеет вид:

=

=

Найдём точки пересечения кривой Михайлова с вещественной и мнимой осями на комплексной плоскости:

при , откуда, то есть мнимую ось кривая Михайлова не пересекает;

при , откуда, при этом. Отложим точку (2;0) на плоскости(рис. 4.1):

Рис. 4.1

Далее находим:

то есть с возрастанием растет быстрее, чем. Получаем кривую Михайлова. Результирующий угол поворота вектораравен. Из формулынаходим, что характеристический многочлен исходного уравнения имееткорня с положительной вещественной частью. Следовательно, решениеисходного уравнения неустойчиво.