- •Методические указания практическим занятиям
- •Практическое занятие №1 Формула Коши
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №2 временные и частотные характеристики автоматических систем (ас)
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №3 структурные схемы автоматических систем (ас)
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №4 теория устойчивости движения
- •Краткие теоретические сведения
- •Теорема Ляпунова об устойчивости по первому приближению
- •Критерий Гурвица
- •Критерий устойчивости Михайлова
- •Задачи для самостоятельного решения
- •Практическое занятие №5 Уравнение Эйлера
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №6 Уравнение Эйлера-Пуассона
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №7 Вариационные задачи на условный экстремум
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №8 Принцип максимума Понтрягина
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №9 Динамическое программирование
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Билиографический список
- •Методические указания к практическим занятиям по дисциплине
Практическое занятие №8 Принцип максимума Понтрягина
Цель занятия: Решение задачи об оптимальном управлении в случае, когда управляющие воздействия ограничены и описываются кусочно-непрерывными функциями.
Краткие теоретические сведения
Постановка задачи. Пусть движение управляемого объекта описывается системой вида:
 (8.1)
(8.1)
где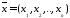 –
траектория развития процесса;
–
траектория развития процесса;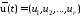 –
вектор управлений, действующих на
систему. Вектор
–
вектор управлений, действующих на
систему. Вектор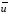 принадлежит некоторой допустимой
области значений
принадлежит некоторой допустимой
области значений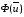 ,
т.е.
,
т.е.
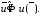 (8.2)
(8.2)
Будем считать заданными :
 ,
(8.3)
,
(8.3)
где
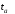 -начальный
момент времени;
-начальный
момент времени;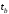 -конечный
момент времени;
-конечный
момент времени;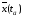 –
начальное положение управляемого
объекта;
–
начальное положение управляемого
объекта; –
не фиксируется.
–
не фиксируется.
Среди
управлений из области (8.2) необходимо
найти оптимальное управление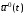 ,которое
минимизирует критерий эффективности:
,которое
минимизирует критерий эффективности:
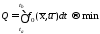 ,
(8.4)
,
(8.4)
где
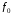 – известная функция своих аргументов.
– известная функция своих аргументов.
Решение.
Введем новую функцию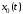 ,
определив ее из решения уравнения:
,
определив ее из решения уравнения:
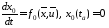 ,
(8.5)
,
(8.5)
тогда
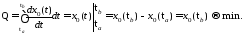
Уравнения (5.1)-(5.5) можно записать в виде основной системы:
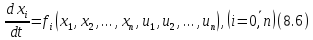
Кроме
нее будем рассматривать еще одну систему,
относительно вспомогательных неизвестных
![]() ,определив
их из решения следующейсопряженной
системы:
,определив
их из решения следующейсопряженной
системы:
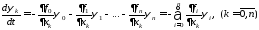 (8.7).
(8.7).
Введем в рассмотрение функцию
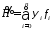 ,
(8.8)
,
(8.8)
тогда с помощью нее системы (8.6) и (8.7) можно записать в виде
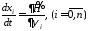 –основная
система,
(8.9)
–основная
система,
(8.9)
 –сопряженная
система.
(8.10)
–сопряженная
система.
(8.10)
Потребуем,
чтобы вектор-функция
 удовлетворяла граничным условиям:
удовлетворяла граничным условиям: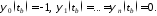
Теорема.
Если
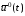 – оптимальное управление, а
– оптимальное управление, а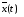 –
соответствующая оптимальная траектория,
минимизирующая критерий (8.4) при уравнениях
движения (8.1), ограничениях (8.2) и краевых
условиях (8.3), то тогда существует
ненулевое решение сопряженной системы
(8.7), т.е.
–
соответствующая оптимальная траектория,
минимизирующая критерий (8.4) при уравнениях
движения (8.1), ограничениях (8.2) и краевых
условиях (8.3), то тогда существует
ненулевое решение сопряженной системы
(8.7), т.е.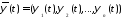 ,
что для любого
,
что для любого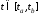 функция (8.8), достигает наибольшего
значения в области (8.2) при
функция (8.8), достигает наибольшего
значения в области (8.2) при ,
т.е.
,
т.е.
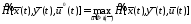 .
.
Решать задачи на нахождение оптимального управления с использованием принципа максимума следует в таком порядке:
1.Составить
функцию
 вида (8.8) и систему (8.10).
вида (8.8) и систему (8.10).
2.Найти
максимум функции
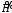 в области (8.2) по переменной
в области (8.2) по переменной .
В результате получим условно-оптимальное
управление:
.
В результате получим условно-оптимальное
управление:
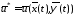 (8.11)
(8.11)
3.Функцию
(8.11) надо подставить в систему (8.10), а
если нужно, то и в систему (8.9), и в
результате получим систему обыкновенных
дифференциальных уравнений относительно
переменных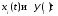 .
.
4.
Решая данную систему (пункта 3) с начальными
условиями (8.3), получаем оптимальную
траекторию .
.
5.Найденные
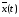 и
и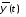 надо подставить в (8.11) и тем самым будет
найдено безусловно оптимальное
управление.
надо подставить в (8.11) и тем самым будет
найдено безусловно оптимальное
управление.
Пример 1.
Решается
задача: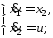 ,
где
,
где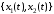 – траектория развития процесса,
– траектория развития процесса,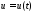 –
управление.
–
управление.
Найти: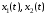 и
и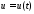 ,
удовлетворяющие условию:
,
удовлетворяющие условию:
W=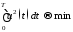 .
.
Решение.
Решим
данную задачу с использованием принципа
максимума. Введем функцию
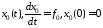 , где
, где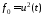 .
.
Тогда исходную систему можно представить в виде
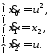
Введем
функцию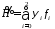 ,где
,где
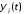 – неизвестные функции времени, тогда
– неизвестные функции времени, тогда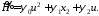
Запишем
сопряженную систему :
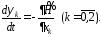 Решении
данной системы в развернутом виде может
быть представлена следующим образом:
Решении
данной системы в развернутом виде может
быть представлена следующим образом:

Запишем
 в явном виде
в явном виде
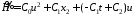
и найдем экстремум этой функции по u :
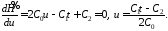
Таким
образом закон изменения оптимального
управления имеет вид
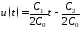
Для нахождения оптимальной траектории движения объекта нужно подставить u(t) в исходную систему, тогда

Пример 2. Использование принципа максимума при решении задач о предельном быстродействии.
Решается
задача: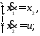 ,
, – траектория движения объекта,
– траектория движения объекта,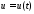 –
управление.
–
управление.
Требуется
найти оптимальное управление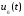 ,
переводящее систему или объект из
некоторого начального состояния
,
переводящее систему или объект из
некоторого начального состояния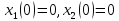 в конечное
в конечное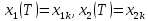 за минимальное время. На управление
наложено ограничение
за минимальное время. На управление
наложено ограничение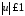 .
.
Решение.
Составим функцию
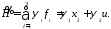 Найдем экстремум этой функции поu:
Найдем экстремум этой функции поu:

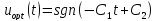 .
.
Например,
если