
4. Множество рациональных чисел в дальнейшем будем обозначать буквой q. Остановимся на рассмотрении свойств этого множества.
Прежде всего отметим, что множество целых чисел Z является подмножеством множества рациональных чисел Q, то есть Z Ì Q.
Действительно,
обозначим через С
множество
рациональных чисел вида
![]() .
Таким образом,
.
Таким образом,
![]() Î
С
тогда и только тогда, когда среди дробей,
эквивалентных
Î
С
тогда и только тогда, когда среди дробей,
эквивалентных
![]() ,
содержится дробь вида
,
содержится дробь вида
![]() ,
так что
,
так что
![]() ~
~
![]() ,
или с
=
аd.
,
или с
=
аd.
Очевидно,
что
![]() =
=
![]() в том и только том
случае, когда a
= b.
Результаты
арифметических операций над элементами
множества С
не
выводят нас из этого множества.
Действительно,
в том и только том
случае, когда a
= b.
Результаты
арифметических операций над элементами
множества С
не
выводят нас из этого множества.
Действительно,
![]() +
+
![]() =
=
![]() .
.
Аналогично:
![]() ×
×
![]() =
=
![]() и
и
![]() –
–
![]() =
=
![]() .
.
Если a
![]() b,
то есть a
= nb,
где n
b,
то есть a
= nb,
где n
![]() Z,
то
Z,
то
![]() :
:
![]() =
=
![]() .
.
Отождествим
рациональное число
![]() с целым числом a.
Тогда множество С
будет совпадать с множеством Z
целых чисел. Операции сложения, умножения
и вычитания определены в нем и обладают
известными свойствами. В дальнейшем
рациональное число
с целым числом a.
Тогда множество С
будет совпадать с множеством Z
целых чисел. Операции сложения, умножения
и вычитания определены в нем и обладают
известными свойствами. В дальнейшем
рациональное число
![]() обозначаем просто через a
и называем целым числом.
обозначаем просто через a
и называем целым числом.
Из того, что Z Ì Q , следует бесконечность множества Q, а также отсутствие в нем наименьшего и наибольшего элементов.
Если
разделить целое число а
=
![]() на
целое число
b
=
на
целое число
b
=
![]() ¹
0, то получим a
:
b
=
¹
0, то получим a
:
b
=
![]() :
:
![]() =
=
![]() .
Следовательно,
рациональное число
.
Следовательно,
рациональное число
![]() есть
частное целых чисел а
и
b
¹
0. Но в таком случае дробь
есть
частное целых чисел а
и
b
¹
0. Но в таком случае дробь
![]() можно рассматривать как частное а
:
b
и наоборот. Поэтому в дальнейшем
рациональное число
можно рассматривать как частное а
:
b
и наоборот. Поэтому в дальнейшем
рациональное число
![]() будем
обозначать
дробью
будем
обозначать
дробью
![]() и понимать как частное двух целых чисел
а
и
b
¹
0.
и понимать как частное двух целых чисел
а
и
b
¹
0.
Приведенные выше правила арифметических действий над рациональными числами в новых обозначениях выглядят следующим образом:
![]() +
+
![]() =
=
![]() ;
;
![]() –
–
![]() =
=
![]() ;
;
![]() ×
×
![]() =
=
![]() ;
;
![]() :
:
![]() =
=
![]() .
.
Если
даны две дроби
![]() и
и
![]() ,
то, используя основное свойство, можем
записать:
,
то, используя основное свойство, можем
записать:
![]() ~
~
![]() и
и
![]() ~
~
![]() .
Очевидно, что дроби
.
Очевидно, что дроби
![]() и
и
![]() имеют одинаковые знаменатели.
имеют одинаковые знаменатели.
Процесс
перехода от дробей
![]() и
и
![]() к эквивалентным им дробям
к эквивалентным им дробям
![]() и
и
![]() с одинаковыми знаменателями называется
приведением
дробей к
общему
знаменателю.
с одинаковыми знаменателями называется
приведением
дробей к
общему
знаменателю.
Если
дроби
![]() и
и
![]() имеют
одинаковые знаменатели, то их сумма и
разность
находятся по следующим правилам:
имеют
одинаковые знаменатели, то их сумма и
разность
находятся по следующим правилам:
![]() +
+
![]() =
=
![]() ;
;
![]() –
–
![]() =
=
![]() .
.
Как
уже отмечалось, всякая дробь может быть
приведена к несократимой дроби с
положительным знаменателем. Поэтому
общность рассуждений не нарушится, если
в дальнейшем всюду будем рассматривать
только дроби с положительными
знаменателями. Если
![]() ,
то дробь
,
то дробь
![]() называется
правильной,
если
же
называется
правильной,
если
же
![]() ,
то неправильной.
,
то неправильной.
Например,
дроби
![]() являются правильными, а дроби
являются правильными, а дроби
![]() – неправильными.
– неправильными.
Теорема
12.
Любое рациональное число
![]() единственным образом представимо в
виде:
единственным образом представимо в
виде:
![]() = q
+
= q
+
![]() ,
где q
–
целое
число, а
,
где q
–
целое
число, а
![]() – правильная несократимая дробь, то
есть 0 ≤ с
<
d,
НОД (с;
d)
= 1.
– правильная несократимая дробь, то
есть 0 ≤ с
<
d,
НОД (с;
d)
= 1.
Доказательство
существования. Прежде
всего заметим, что считаем b
> 0. Далее разделим а
с
остатком
на b
и получим а
= bq
+ r,
0 < r
< b.
Тогда
![]() = q
+
= q
+
![]() .
Пусть НОД(r,
b)
=
k,
тогда
r
= kc,
b
= kd,
где НОД(с,
d)
= 1.
Сокращая дробь
.
Пусть НОД(r,
b)
=
k,
тогда
r
= kc,
b
= kd,
где НОД(с,
d)
= 1.
Сокращая дробь
![]() на k,
получим
на k,
получим
![]() = q
+
= q
+
![]() ,
что и дает требуемое представление.
,
что и дает требуемое представление.
Доказательство
единственности. Пусть
имеем два указанных представления
рационального числа
![]() :
:
![]() = q1
+
= q1
+
![]() и
и
![]() = q2
+
= q2
+
![]() ,
здесь 0 ≤ с1
<
d1,
НОД (с1;
d1)
= 1, 0 ≤ с2
<
d2,
НОД (с2;
d2)
= 1. Тогда а
= bq1
+
,
здесь 0 ≤ с1
<
d1,
НОД (с1;
d1)
= 1, 0 ≤ с2
<
d2,
НОД (с2;
d2)
= 1. Тогда а
= bq1
+
![]() и а
= bq2
+
и а
= bq2
+
![]() .
Так как а
–
целое число, bq1
и bq2
также
целые числа, то
.
Так как а
–
целое число, bq1
и bq2
также
целые числа, то
![]() и
и
![]() являются целыми числами. Кроме того, в
силу единственности деления с остатком,
можем записать равенства: bq1
= bq2
и
являются целыми числами. Кроме того, в
силу единственности деления с остатком,
можем записать равенства: bq1
= bq2
и
![]() =
=
![]() или q1
= q2
и
или q1
= q2
и
![]() =
=
![]() .
.
Из
последнего равенства можем записать:
![]() ;
;
![]() .
Поскольку НОД (с1;
d1)
= 1 и НОД (с2;
d2)
= 1, то d1
.
Поскольку НОД (с1;
d1)
= 1 и НОД (с2;
d2)
= 1, то d1
![]() d2
и
d2
d2
и
d2
![]() d1.
Но d1
> 0 и d2
> 0, а значит, деление возможно только
при условии d1
= d2.
Отсюда
имеем с1
= с2.
d1.
Но d1
> 0 и d2
> 0, а значит, деление возможно только
при условии d1
= d2.
Отсюда
имеем с1
= с2.
Итак, мы установили, что q1 = q2, d1 = d2, с1 = с2, то есть единственность доказана.
Рассмотрим
примеры:![]() .
.
Последнее равенство можно переписать иначе:

Числа
вида
![]() и
и
![]() записываются, соответственно,
записываются, соответственно,
![]() и
и
![]() и называются смешанными
числами.
и называются смешанными
числами.
Таким образом, любая неправильная дробь может быть единственным образом записана в виде смешанного числа.
Теорема
13.
Если
дроби
![]() и
и
![]() представляют одно и то же рациональное
число, то произведения аb
и
cd
имеют
один и тот же знак
или равны нулю одновременно.
представляют одно и то же рациональное
число, то произведения аb
и
cd
имеют
один и тот же знак
или равны нулю одновременно.
Доказательство.
Прежде
всего, напомним, что эквивалентность
дробей
![]() и
и
![]() означает справедливость равенства ad
=
bc.
Рассмотрим
два случая.
означает справедливость равенства ad
=
bc.
Рассмотрим
два случая.
1. Пусть ab ¹ 0, тогда a ¹ 0. Кроме того, d ¹ 0 как знаменатель дроби. Следовательно, ad ¹ 0, но тогда из равенства ad = bс следует, что bс ¹ 0, а так как b > 0, то с ¹ 0. Далее рассмотрим произведение (ab)(cd) = (ad) (bс) = (bс)2 > 0, из которого следует, что ab и cd имеют одинаковые знаки.
2. Пусть теперь аb = 0, тогда a = 0, поскольку b ¹ 0 как знаменатель дроби. Но, в таком случае, из равенства ad = bс = 0 следует, что bс = 0, а поскольку b ¹ 0, имеем с = 0. Это означает, что cd= 0 и теорема доказана.
Определение
19.
Рациональное число
![]() (b
> 0) называется положительным,
если
a
> 0, и отрицательными, если а
< 0.
(b
> 0) называется положительным,
если
a
> 0, и отрицательными, если а
< 0.
Поскольку
произведение аb
является
целым числом, то оно удовлетворяет точно
одному из условий: аb
> 0; аb
< 0; аb
= 0. Но тогда, согласно теореме 13, для
![]() также выполняется точно одно из трех
условий:
также выполняется точно одно из трех
условий:
![]() положительно;
положительно;
![]() отрицательно;
отрицательно;
![]() – нуль.
– нуль.
Множество положительных рациональных чисел будем обозначать символом Q+, а множество отрицательных рациональных чисел – символом Q–.Таким образом, Q = Q_ È {0} È Q+.
Теорема 14. Сумма и произведение положительных рациональных чисел являются положительными рациональными числами.
Доказательство.
Положительность чисел
![]() и
и
![]() означает выполнимость условий аb
> 0 и cd
> 0. Умножая обе части первого неравенства
на d2
> 0, а второго – на b2
> 0 и складывая их, получим abd2
+
cdb2
> 0. Последнее неравенство можно записать
в виде (ad
+ bc)bd
> 0,
что означает положительность числа
означает выполнимость условий аb
> 0 и cd
> 0. Умножая обе части первого неравенства
на d2
> 0, а второго – на b2
> 0 и складывая их, получим abd2
+
cdb2
> 0. Последнее неравенство можно записать
в виде (ad
+ bc)bd
> 0,
что означает положительность числа
![]() +
+
![]() =
=
![]() .
.
Аналогично
из неравенств аb
> 0 и cd
>
0 следует, что (ab)(cd)
=
(ac)(bd)
>
0. Последнее неравенство означает
положительность числа
![]() ·
·
![]() =
=
![]() ,
и справедливость теоремы доказана.
,
и справедливость теоремы доказана.
Определение
20.
Говорят,
что рациональное число
![]() меньше
рационального числа
меньше
рационального числа
![]() ,
если существует положительное рациональное
число
,
если существует положительное рациональное
число
![]() такое, что выполняется равенство
такое, что выполняется равенство
![]() +
+
![]() =
=
![]() .
.
![]() .
.
Если
![]() меньше
меньше
![]() ,
то говорят также, что
,
то говорят также, что
![]() больше
больше
![]() и пишут:
и пишут:
![]() >
>
![]() .
.
Символы ≤ и ³ понимаются так же, как и во множестве целых неотрицательных чисел. Из данного определения вытекают важные следствия, выражающие правила сравнения дробей.
Следствие
1.
![]() .
.
Доказательство.
Пусть
![]() <
<
![]() ,
тогда, по определению 20, существует
положительное рациональное число
,
тогда, по определению 20, существует
положительное рациональное число
![]() такое, что выполняется равенство
такое, что выполняется равенство
![]() +
+
![]() =
=
![]() .
По правилу сложения дробей
.
По правилу сложения дробей
![]() ,
откуда следует, что and+bmd
=
bnc.
Обе
части последнего равенства разделим
на число п
¹
0. Полученное равенство ad
+ bd
·
,
откуда следует, что and+bmd
=
bnc.
Обе
части последнего равенства разделим
на число п
¹
0. Полученное равенство ad
+ bd
·
![]() = bc
означает,
что ad
< bс,
так
как bd
·
= bc
означает,
что ad
< bс,
так
как bd
·
![]() > 0.
> 0.
Справедливость обратного утверждения вытекает из того, что все преобразования, приведенные в первой части доказательства, выполнимы в обратном порядке. Таким образом, справедливость следствия можно считать доказанной.
Следствие
2.
Если
n
Î
N, то
![]() ,
,
то есть из двух дробей с одинаковыми положительна знаменателями меньше та, у которой меньше числитель.
Справедливость
этого утверждения легко доказать, если
учесть, что дроби всегда можно привести
к общему знаменателю. А значит, общность
не нарушится, если будем считать, что
из неравенства
![]() следует существование положительного
рационального числа
следует существование положительного
рационального числа
![]() ,
такого, что
,
такого, что
![]() +
+
![]() =
=
![]() .
Далее, по правилу сложения дробей, можем
записать равенство
.
Далее, по правилу сложения дробей, можем
записать равенство
![]() .
Откуда,
учитывая определение равенства дробей,
имеем а
+ т = b.
Так
как m
> 0, то из последнего равенства следует,
что а
< b.
.
Откуда,
учитывая определение равенства дробей,
имеем а
+ т = b.
Так
как m
> 0, то из последнего равенства следует,
что а
< b.
Аналогично доказывается справедливость обратного утверждения.
Определение
21.
Рациональное число
![]() называется противоположным
рациональному
числу
называется противоположным
рациональному
числу
![]() ,
если выполняется равенство
,
если выполняется равенство
![]() +
+
![]() = 0.
= 0.
Число,
противоположное числу
![]() ,
будем обозначать –
,
будем обозначать –
![]() .
.
Аналогично определению 8 модуля целого числа можно сформулировать определение модуля рационального числа.
Теорема
15.
Для любых
![]() ,
,
![]() Î
Q
имеет
место точно одно из трех соотношений:
Î
Q
имеет
место точно одно из трех соотношений:
![]() <
<
![]() ;
;
![]() =
=
![]() ;
;
![]() <
<![]() .
.
Доказательство.
Рассмотрим
разность
![]() –
–
![]() .
Она, как известно из теоремы 10, является
числом рациональным и имеет вид
.
Она, как известно из теоремы 10, является
числом рациональным и имеет вид
![]() .
Согласно определению 19, рациональное
число
.
Согласно определению 19, рациональное
число
![]() может быть числом положительным, равным
нулю или отрицательным. По определению
разности (17), можем записать равенство
может быть числом положительным, равным
нулю или отрицательным. По определению
разности (17), можем записать равенство
![]() =
=
![]() +
+
![]() ,
из которого следуют 3 случая:
,
из которого следуют 3 случая:
1. Если
![]() > 0, то, по определению 20,
> 0, то, по определению 20,
![]() <
<
![]() .
.
2.
Если
![]() = 0, то, по правилу сложения с нулем,
= 0, то, по правилу сложения с нулем,
![]() =
=
![]() .
.
3. Если
![]() < 0, то рациональное число –
< 0, то рациональное число –
![]() > 0 или
> 0 или
![]() > 0. Далее рассмотрим разность
> 0. Далее рассмотрим разность
![]() –
–
![]() .
Она выражается рациональным числом
.
Она выражается рациональным числом
![]() .
Пользуясь определением разности, можем
также записать равенство
.
Пользуясь определением разности, можем
также записать равенство
![]() =
=
![]() +
+
![]() ,
из которого следует, что
,
из которого следует, что
![]() <
<
![]() ,
и справедливость теоремы доказана.
,
и справедливость теоремы доказана.
Теорема 16. Бинарное отношение «меньше» (больше) на множестве Q обладает свойством транзитивности:
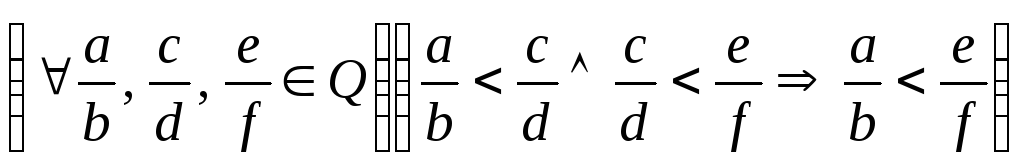 .
.
Доказательство. Пользуясь определением 20 отношения «меньше», можем записать:
![]() ;
;
![]() .
.
Из двух последних равенств имеем:
![]() , или
, или
![]() .
.
Поскольку
![]() ,
то, по определению отношения «меньше»,
можем записать, что
,
то, по определению отношения «меньше»,
можем записать, что
![]() <
<
![]() ,
и транзитивность доказана.
,
и транзитивность доказана.
Аналогично можно доказать транзитивность отношения «больше».
Таким образом, рассмотренные отношения «меньше» и «больше» на множестве рациональных чисел Q обладают свойствами асимметричности, транзитивности и связности, а значит, являются отношениями строгого линейного порядка.
Итак, множество рациональных чисел Q является линейно упорядоченным.
Теорема 17. Между двумя различными числами из множества Q заключено бесконечно много чисел того же множества.
Доказательство.
Рассмотрим
два произвольно выбранных рациональных
числа. Не нарушая общности рассуждений,
представим эти числа дробями
![]() и
и
![]() ,
имеющими общий знаменатель. Для
определенности положим, что
,
имеющими общий знаменатель. Для
определенности положим, что
![]() <
<
![]() .
Из последнего неравенства следует, что
а
<
b.
Рассмотрим
рациональное число, представляемое
дробью
.
Из последнего неравенства следует, что
а
<
b.
Рассмотрим
рациональное число, представляемое
дробью
![]() .
Так как а
< b,
то
2а
< а
+ b
< 2b,
a
поскольку п
> 0,
можем записать
.
Так как а
< b,
то
2а
< а
+ b
< 2b,
a
поскольку п
> 0,
можем записать
![]() ,
или
,
или
![]() .
.
Итак, мы показали, что между любыми двумя числами из множества Q заключено хотя бы одно число, также принадлежащее множеству Q.
Далее,
рассматривая числа
![]() и
и
![]() ,
можно указать хотя бы одно рациональное
число, заключенное между ними. Аналогично
для чисел
,
можно указать хотя бы одно рациональное
число, заключенное между ними. Аналогично
для чисел
![]() и
и
![]() .
Продолжая описанный процесс, мы найдем
между числами
.
Продолжая описанный процесс, мы найдем
между числами
![]() и
и
![]() бесконечно много различных чисел из
множества Q.
бесконечно много различных чисел из
множества Q.
Теорема 17 выражает свойство, называемое плотностью.
Теорема
18.
Для любых двух рациональных чисел
![]() > 0 и
у
=
> 0 и
у
=
![]() найдется
натуральное число п
такое,
что выполняется неравенство пх
> у.
найдется
натуральное число п
такое,
что выполняется неравенство пх
> у.
Доказательство. Рассмотрим два случая.
1.
Если
![]() >
>
![]() ,
то достаточно взять п
= 1,
так как 1 ·
,
то достаточно взять п
= 1,
так как 1 ·
![]() =
=
![]() >
>
![]() .
.
2. Если
же 0 <
![]() ≤
≤
![]() ,
то по следствию 1 из определения 20 0 <
ad
≤
bc.
Во множестве целых чисел выполняется
свойство Архимеда, то есть для положительных
целых чисел ad
и
bс
найдется
натуральное
число n
такое, что nad
>
bc.
Из последнего неравенства следует: n
·
,
то по следствию 1 из определения 20 0 <
ad
≤
bc.
Во множестве целых чисел выполняется
свойство Архимеда, то есть для положительных
целых чисел ad
и
bс
найдется
натуральное
число n
такое, что nad
>
bc.
Из последнего неравенства следует: n
·
![]() =
=
![]() >
>
![]() .
Теорема доказана.
.
Теорема доказана.
Свойство множества рациональных чисел, выраженное теоремой 18, называется свойством Архимеда.
Таким образом установлено, что множество Q рациональных чисел обладает следующими свойствами: оно бесконечное, линейно упорядоченное, плотное, в нем нет наибольшего и наименьшего чисел и выполняется свойство Архимеда.
Кроме того, множество рациональных чисел Q образует числовое поле относительно операций сложения и умножения.
5.
Рассмотрим
прямую l
и точку О
на
ней. Выберем отрезок е
= ОА в
качестве единицы измерения. Прямая l
разбивается точкой
О
на
два луча: положительный (правый) – тот,
на котором находится точка А,
и
отрицательный (левый). Рациональному
числу х
=
![]() (n
Î
N)
поставим
в соответствие точку М
=
M
(x)
на прямой l
по
следующему правилу.
(n
Î
N)
поставим
в соответствие точку М
=
M
(x)
на прямой l
по
следующему правилу.
Разбиваем
единичный отрезок е
= ОА на
n
равных частей. Пусть e1
= ОВ
– одна
из этих частей, так что е
= пе1.
Последнее
равенство будем также записывать в
виде:
![]() .
.
O e1 B A M

e x
Рис. 4
Если m > 0, то откладываем отрезок e1 от точки О вправо m раз. В результате получим точку М на положительном луче (рис. 4).
Если же m < 0 , то откладываем отрезок e1 от точки О влево |m| раз. Точка М в этом случае будет лежать на отрицательном луче.
Найденную таким
образом точку М поставим в соответствие
числу х =
![]() .
При этом число х =
.
При этом число х =
![]() называем координатой точки М.
называем координатой точки М.
Отрезок ОМ будем считать направленным, то есть точка О считается началом этого отрезка, а точка М – его концом.
Два
направленных отрезка ОМ
и
ОР
называются
равными
(пишут ОМ
= ОР)
тогда
и только тогда, когда равны их длины и
совпадают направления. Учитывая это
соглашение, можем записать: ОМ
= m
e1.
А
поскольку e1
=
![]() ,
то окончательно имеем ОМ
=
,
то окончательно имеем ОМ
=
![]() е.
Последнее равенство
надо понимать следующим образом: длина
отрезка ОМ
равна
модулю числа
е.
Последнее равенство
надо понимать следующим образом: длина
отрезка ОМ
равна
модулю числа
![]() ;
отрезок ОМ
направлен
в ту же сторону, что и отрезок е
= ОА, если
;
отрезок ОМ
направлен
в ту же сторону, что и отрезок е
= ОА, если
![]() > 0, и в сторону, противоположную е,
если
> 0, и в сторону, противоположную е,
если
![]() < 0.
< 0.
Итак, каждому
рациональному числу х =
![]() поставлена а соответствие точка М
= М(х)
прямой l.
Отметим ряд свойств этого соответствия.
поставлена а соответствие точка М
= М(х)
прямой l.
Отметим ряд свойств этого соответствия.
1) Каждому
рациональному числу соответствует
единственная точка на прямой l.
Другими словами, если дробь х
=
![]() несократима и М
= М(х)
– соответствующая ей точка, то дроби
несократима и М
= М(х)
– соответствующая ей точка, то дроби
![]() =
=
![]() ,
где р
Î
N,
будет отвечать та же самая точка М
прямой
l.
Действительно, пусть М*
– точка, отвечающая числу
,
где р
Î
N,
будет отвечать та же самая точка М
прямой
l.
Действительно, пусть М*
– точка, отвечающая числу
![]() .
Покажем, что точки М
и М*
лежат
на одном и том же луче прямой l,
поскольку числа
.
Покажем, что точки М
и М*
лежат
на одном и том же луче прямой l,
поскольку числа
![]() и
и
![]() имеют один и тот же знак.
имеют один и тот же знак.
Далее,
для того чтобы найти точку М*,
соответствующую числу
![]() ,
следует разделить отрезок е
на
рп
равных
частей (или, что то же самое, отрезок е1
=
,
следует разделить отрезок е
на
рп
равных
частей (или, что то же самое, отрезок е1
=
![]() разделить
еще на р
равных
частей) и полученный таким образом
отрезок
разделить
еще на р
равных
частей) и полученный таким образом
отрезок
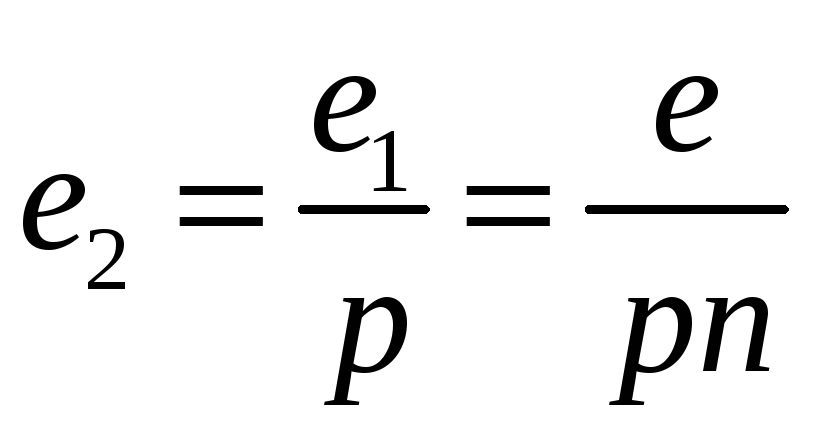 отложить от точки О
отложить от точки О
![]() раз
в соответствующем направлении.
раз
в соответствующем направлении.
Но
отрезок ОМ,
построенный для дроби
![]() ,
представляет собой сумму
,
представляет собой сумму
![]() отрезков,
каждый из которых по длине равен отрезку
е1,
а отрезок е1,
в
свою очередь, есть сумма р
отрезков,
равных
отрезков,
каждый из которых по длине равен отрезку
е1,
а отрезок е1,
в
свою очередь, есть сумма р
отрезков,
равных
 ,
а значит ОМ
представляет
собой сумму
,
а значит ОМ
представляет
собой сумму
![]() отрезков, равных по длине е2.
Так
что точки М*
и
М
совпадают.
отрезков, равных по длине е2.
Так
что точки М*
и
М
совпадают.
2) Различным рациональным числам соответствуют различные точки прямой l.
Рассмотрим
два различных рациональных числа,
представленных дробями х1
=
![]() и х2
=
и х2
=
![]() ,
где b
>
0, d
>
0. Поскольку
,
где b
>
0, d
>
0. Поскольку
![]() ¹
¹
![]() ,
то ad
¹
bс.
Покажем, что соответствующие им точки
М1
= М(х1)
и
М2
= М(х2)
на
прямой l
также различны.
,
то ad
¹
bс.
Покажем, что соответствующие им точки
М1
= М(х1)
и
М2
= М(х2)
на
прямой l
также различны.
Доказательство
проведем методом от противного.
Предположим, что М(х1)
= М(х2)
= М.
Поскольку
х1
=
![]() – координата точки М,
то, разбив единичный отрезок е
на
b
равных
частей, получим отрезок е1
такой,
что е
=
bе1
и
ОМ
= aе1.
Аналогично, поскольку
– координата точки М,
то, разбив единичный отрезок е
на
b
равных
частей, получим отрезок е1
такой,
что е
=
bе1
и
ОМ
= aе1.
Аналогично, поскольку
![]() – координата той же самой точки М,
найдем
отрезок е2,
такой, что
е
= d
е2
и
ОМ
= се2.
Из
равенств ОМ
= ае1
и
ОМ
= се2
имеем:
ае1
= се2.
Умножая
последнее равенство на bd
¹
0, получим ad(bе1)
= cb(dе2).
Откуда,
учитывая, что е
=
bе1
и
е
= de2,
находим ade
= cbe,
что влечет за собой равенство ad
= bс,
а
значит,
– координата той же самой точки М,
найдем
отрезок е2,
такой, что
е
= d
е2
и
ОМ
= се2.
Из
равенств ОМ
= ае1
и
ОМ
= се2
имеем:
ае1
= се2.
Умножая
последнее равенство на bd
¹
0, получим ad(bе1)
= cb(dе2).
Откуда,
учитывая, что е
=
bе1
и
е
= de2,
находим ade
= cbe,
что влечет за собой равенство ad
= bс,
а
значит,
![]() =
=
![]() .
Пришли к противоречию с условием
.
Пришли к противоречию с условием
![]() ¹
¹
![]() .
Требуемое доказано.
.
Требуемое доказано.
3)
Целому числу k
=![]() отвечает
та же самая точка М
Î
l,
которая
была поставлена ему в соответствие.
отвечает
та же самая точка М
Î
l,
которая
была поставлена ему в соответствие.
Действительно,
поскольку знаменатель дроби
![]() равен
единице, то откладываем единичный
отрезок е
целиком (не деля его на части) от
равен
единице, то откладываем единичный
отрезок е
целиком (не деля его на части) от
![]() раз от точки О
вправо,
если k
>
0 , и влево, если k
< 0.
В результате получаем точку М,
координатой которой будет число k.
раз от точки О
вправо,
если k
>
0 , и влево, если k
< 0.
В результате получаем точку М,
координатой которой будет число k.
