
К решению задач по электричеству
.pdf
2.36. Пространство между двумя концентрическими сферами, радиусы которых R1 и
a
R2 (R2 R1), заряжено с объемной плотностью r3 , где a- постоянная величина.
Найдите полный заряд сферического слоя, а также напряженность электростатического поля.
Ответ: q 8 aln |
R2 |
, E |
2a |
ln |
R2 |
|
1 |
. |
||
R |
|
R |
|
|||||||
|
|
|
0 |
|
|
r |
2 |
|
||
1 |
|
|
|
1 |
|
|
|
|||
§3. Поле в диэлектрике
I. Краткие теоретические сведения
В диэлектриках (изоляторах) нет свободных электрических зарядов. Они состоят из нейтральных атомов или молекул. Заряженные частицы в нейтральном атоме связаны друг с другом и не могут перемещаться под действием электрического поля по всему объему диэлектрика.
Вектор диэлектрического смещения (электрическая индукция)
D 0E P.
где E - вектор напряженности электрического поля, P - вектор поляризации,
0 0,885 10 11 Ф/м.
При внесении диэлектрика во внешнее электрическое поле E0 в нем возникает не-
которое перераспределение зарядов, входящих в состав атомов или молекул. В результате такого перераспределения на поверхности диэлектрического образца появляются избыточные нескомпенсированные связанные заряды. Все заряженные частицы, образующие макроскопические связанные заряды, по-прежнему входят в состав своих ато-
мов. Связанные заряды создают электрическое поле E которое внутри диэлектрика
направлено противоположно вектору напряженности E0 внешнего поля. Этот процесс называется поляризацией диэлектрика. В результате полное электрическое поле
E E0 E внутри диэлектрика оказывается по модулю меньше внешнего поля E0 .
Теорема Гаусса для P в интегральной форме: поток вектора P сквозь произвольную замкнутую поверхность S равен взятому с обратным знаком избыточному свя-
занному заряду диэлектрика в объеме, охватываемом поверхностью S .
 PdS q .
PdS q .
S
Теорема Гаусса для D в интегральной форме:
 DndS q .
DndS q .
S
Теорема Гаусса означает, что поток вектора D через любую замкнутую поверхность S равен полному свободному заряду внутри поверхности. Эта теорема оказывается
справедливой для любой замкнутой поверхности, в том числе и такой, которая пересекает границу разных диэлектриков или границу диэлектрика с проводником. Заметим,
что поток вектора D равен нулю в отсутствие свободных зарядов внутри поверхности.
Теорема Гаусса для электрической индукции D в дифференциальной форме:
divD 0divE divP 0 ,
0
т.е. дивергенция электрической индукции D определяется только плотностью свободного заряда.
Граничные условия общего вида для электрического поля:
D1n D2n |
0 1E1n 0 2E2n ; |
|
E1 E2 |
D1 0 1 D2 0 2 . |
|
Для изотропных диэлектриков |
|
|
P 0E, |
D 0E, |
1 . |
- диэлектрическая восприимчивость, - диэлектрическая проницаемость.
II. Примеры решения задач
Пример 3.1. Точечный сторонний заряд q находится в центре шара из однородного диэлектрика с проницаемостью . Найти поляризованность P как функцию радиусвектора r относительно центра шара, а также связанный заряд q внутри сферы, ра-
диус которой меньше радиуса шара.
Решение.
Для изотропных диэлектриков связь вектора поляризованности P с вектором на-
пряженности E имеет вид
P 1 0E .
Так как в условии задачи дан сторонний заряд, то следует использовать теорему
Гаусса для вектора D . По теореме при r R
D |
1 |
|
|
q . |
|||||
|
4 r2 |
||||||||
|
|
|
|
|
|
|
|||
Напряженности E найдем как |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
q |
|
r |
. |
||
E |
|
|
|
|
|||||
4 0 |
|
r2 |
|
||||||
|
|
|
r |
||||||
Подставляя последнее выражение, получим искомую зависимость вектора поляризо-
ванности P от радиус-вектора r при r R
|
1 |
q |
r . |
||
P |
|||||
|
|
4 r3 |
|||
|
|
||||
Для нахождения заряда внутри сферы радиуса r воспользуемся теоремой Гаусса для вектора P . Получим
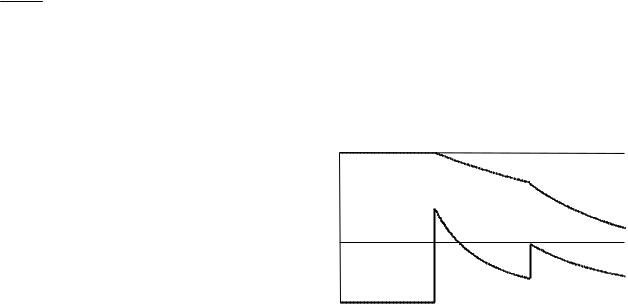
|
|
|
1 4 r |
2 |
|
1 |
q . |
|||
|
|
|
|
|
|
|
|
|
||
q |
|
|
|
4 r |
2 q |
|
||||
|
|
|||||||||
Пример 3.2. Показать, что на границе однородного диэлектрика с проводником поверхностная плотность связанных зарядов 1 / , где - диэлектрическая
проницаемость, - поверхностная плотность зарядов на проводнике. Решение.
Применим теорему Гаусса для напряженности электрического поля E в веществе
 0EndS q q .
0EndS q q .
S
На границе раздела в качестве замкнутой поверхности выберем цилиндр, ось которого перпендикулярна границе. Так как внутри проводника электрическое поле от-
сутствует E 0, то через боковую поверхность цилиндра поток также будет равен нулю. Тогда
0En S S .
Применим теорему Гаусса для D для той же поверхности, учитывая что в про-
воднике D 0. Получим
Dn S S .
Отсюда имеем 0En .
1 .
Пример 3.3. Однородный диэлектрик имеет вид сферического слоя с радиусами a и b, причем a b . Изобразить примерные графики модуля напряженности электрического поля E и потенциала как функции расстояния r от центра системы, если диэлектрик имеет положительный сторонний заряд, распределенный равномерно по внутренней поверхности слоя.
Решение.
Применим теорему Гаусса для электрической индукции D , выбрав в качестве поверхности сферу радиуса r. Тогда при
|
r a: |
D4 r2 0, |
D 0, |
|
E 0; |
|
|
|
|
||||||||
a r b: |
D4 r2 q, |
D |
q |
, |
E |
D |
|
1 |
|
q |
; |
||||||
4 r2 |
|
|
|
r2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
0 |
4 0 |
|
|
|||||
|
|
r a: |
E |
|
|
1 |
|
|
q |
; |
|
|
|
|
|
||
|
|
4 0 |
|
|
a2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
r b: |
|
E |
|
1 |
|
|
q |
; |
|
|
|
|
|
||
|
|
|
4 0 r2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
q |
, |
|
|
|
|
|
со стороны r b; |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
0 b |
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
r b: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
E |
|
|
1 |
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
1, со стороны r b. |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
b |
2 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Связь между потенциалом и напряженностью электрического поля E имеет вид |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
Таким образом, получаем |
|
|
Edr 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
r a: |
|
|
|
|
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
a r b: |
|
|
|
|
1 |
|
|
|
|
q |
|
С ; |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
r |
1 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
r b: |
|
|
|
|
|
0 |
1 |
|
q |
С2. |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Постоянные интегрирования C1 |
и C2 найдем из условия непрерывности потенциа- |
||||||||||||||||||||||||||||||||||||||||||||||||||||
ла на границах r a |
и r b . |
При |
|
r a |
|
найдем |
С |
|
1 |
|
q |
. |
Соответственно, |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
4 0 |
a |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
при r b |
получаем |
C2 |
1 |
|
1 |
|
1 |
|
. |
|
Из условия 0 |
при r найдем |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
b |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 0 a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
q |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 0 |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
С учетом полученных значений C1 |
и C2 |
запишем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r a: |
|
|
|
|
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
a r b: |
1 0 |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
r |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
r b: |
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
q |
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Видно, |
что при 0 0 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
и |
уменьшается |
с |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ростом |
|
|
расстояния |
r, |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 .Схематические |
||||
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
графики зависимости E(r) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и (r) |
приведены на рис. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.1. Из графиков следует, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
что потенциал (r) изме- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
няется непрерывно, а зави- |
|||||||
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
симость |
|
|
напряженности |
||||||||||||||
Рис. 3.1
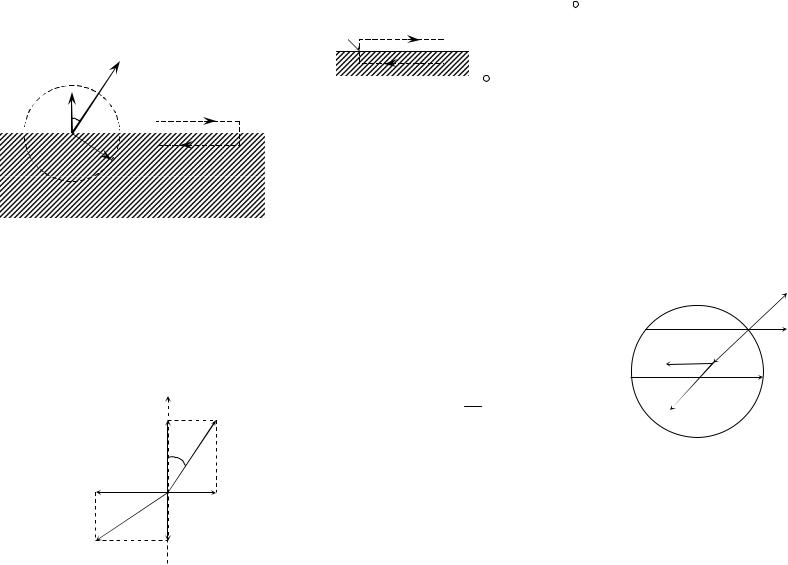
E(r) имеет скачки, что связано с изменением диэлектрической проницаемости при переходе из одной среды в другую.
Пример 3.4. У плоской поверхности однородного диэлектрика с проницаемостью напряженность электрического поля в вакууме равна E0, причем вектор E0 составляет
угол |
с |
нормалью |
к поверхности |
|
|
|
|
|
E0 |
|
|
|
|
диэлектрика (рис. 3.2). Считая поле |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
||||||||
внутри и вне диэлектрика однород- |
|
n |
|
|
|
|
l |
|
|
||||
ным, найти: |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Г |
|||||||
а) поток вектора |
E0 через сферу |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
радиуса R с центром на поверхности |
|
|
|
R |
|
|
|
|
|
|
|||
диэлектрика; |
|
|
|
|
|
|
|
|
|
|
|
||
б) |
циркуляцию |
вектора D по |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
контуру Г |
длины l |
(см. рис. 3.3), |
|
|
|
|
|
|
|
|
|
|
|
плоскость которого перпендикулярна |
|
|
|
|
|
|
|
|
|
|
|||
к поверхности диэлектрика и парал-
Рис. 3.2
лельна вектору E0 .
Решение.
а). Применим теорему Гаусса для вектора E :
 0EndS q q .
0EndS q q .
S
На границе раздела в качестве замкнутой поверхности выберем цилиндр, ось которого перпендикулярна границе, тогда
0EndS dS .
Для нахождения поверхностной плотности связанных зарядов , воспользуемся теоремой Гаусса для
вектора P для той же поверхности
Pn 1 0En .
Разложим вектор E и E0 на нормальные и тан-
генциальные составляющие как показано на рис. 3.3. Применяя граничные условия, имеем
En |
E0n |
|
E0 cos |
. |
||
|
|
|
||||
|
|
|
|
|
||
Тогда |
|
|
|
|
||
|
1 |
|
0E0 cos . |
|||
|
||||||
|
|
|
|
|
|
|
n |
|
|
E0n |
E |
0 |
|
|
|
E
E E0
En
Рис. 3.3
Учитывая, что 0 окончательно получим
|
|
|
|
|
|
|
1 |
|
|
|
|
|
D 1 |
EndS |
E |
0 cos R2 . |
|||
|
|
|
|
||||||
|
|
l |
S |
|
|
|
|||
l |
|
|
Г |
б). Найдем циркуляцию вектора D по контуру Г |
|||||
|
|
|
|||||||
|
|
|
|||||||
длины l (см. рис. 3.4)
|
|
|
l |
D 2 |
Ddr D 1l Dnl D 2l Dnl D 1 D 2 |
||
Г |
|
|
|
Рис. 3.4 |
Применяя граничные условия, имеем |
|
|
D 1 0E0 0E0 sin , |
D 2 0E0 , |
|
|
получим
 Ddr 0 1lE0 sin .
Ddr 0 1lE0 sin .
Г
Пример 3.5. Круглый диэлектрический диск радиуса R и толщины d поляризован
статически так, что поляризованность, равная P , всюду одинакова и вектор P лежит в плоскости диска. Найти напряженность E электрического поля в центре диска, если d R.
Решение. Из рис. 3.5 следует, что
Pn P cos , dEx dE cos .
Выделим элемент dl, заряд которого будет равен dq dld . Тогда напряженность поля элементарного заряда можно найти как
dq dE k , R2
тогда
n
dl 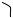
 P
P
dEx |
|
 dE
dE
dE |
|
dE cos k |
dld |
cos k |
Rd d |
cos k |
Pcos2 |
|
d d |
||||
|
|
|
R |
|
|||||||||
|
x |
|
R2 |
R2 |
|
|
|
|
Рис. 3.5 |
||||
|
|
. |
|
|
|
|
|
|
|
|
|
||
Отсюда |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2 |
|
Pd |
|
|
Pd |
||||
|
|
|
|
Ex dEx |
|
2 cos2 d |
|
||||||
|
|
|
|
k |
|
|
. |
||||||
|
|
|
|
R |
4R 0 |
||||||||
|
|
0 |
|
|
|
|
0 |
|
|
|
|
||
Из рис. 3.6 следует, что векторы Px и Ex параллельны, но направлены в противоположные стороны, тогда
|
Pd |
. |
|
E |
|||
|
|||
|
4R 0 |
||
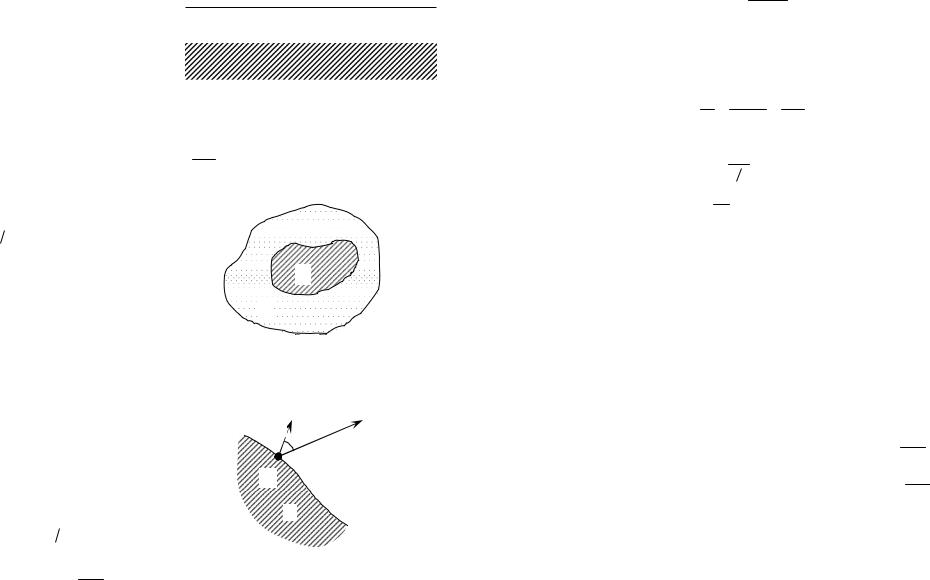
Пример 3.6. Первоначально пространство между обкладками плоского конденсатора заполнено воздухом и напряженность поля в зазоре равна E0 . Затем половину зазора, как показано на рис. 3.6, заполнили однородным изотропным диэлектриком с проницаемостью . Найти модули век-
торов E и D в обеих частях зазора (1 |
1 |
|
|
|
|
и 2), если при введении диэлектрика: |
|
|
|
|
|
а) напряжение между обкладками |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
не менялось; |
|
|
|
||
|
|
|
|||
б) заряды на обкладках оставались |
|
|
|
|
|
неизменными. |
|
|
Рис. 3.6 |
||
Решение. |
|
|
|
|
|
а). В начальный момент емкость конденсатора
С 0S . d
При заполнении диэлектриком, получаем два конденсатора, включенных последовательно. Их емкости соответственно равны
С |
0S |
|
2 0S |
, |
С |
|
|
2 0S |
С . |
|
|
|
d |
||||||
1 |
d 2 d |
|
2 |
|
1 |
||||
Суммарная емкость
С12 |
|
С1С2 |
|
С1 |
. |
С1 С2 |
|
||||
|
|
1 |
|||
В начальный момент напряжение между обкладками U0 E0d . При введении диэлек-
трика напряжение не изменилось (согласно условию задачи), но теперь оно приложено к двум последовательно соединенным конденсаторам. При этом заряд на обкладках q12 C12U0 . Тогда напряжение на конденсаторе C1 равно
U |
q12 |
|
C12U0 |
U |
|
|
. |
C |
|
|
|||||
1 |
|
C |
0 1 |
||||
|
1 |
1 |
|
|
|
|
|
Следовательно, напряженность электрического поля на конденсаторе C1
E |
U1 |
2E |
|
|
. |
|
|
||||
1 |
d 2 |
0 1 |
|||
Аналогично, легко получить
E2 2E0 . 1
q
Рис. 3.7
n |
0 |
E0 |
|
A
Рис. 3.8
Применяя граничные условия для границы раздела диэлектрик-вакуум с учетом D1 0E1 , найдем
D1 D2 2E0 0 .
1
б). В начальный момент заряд
q C0U0 C0E0d .
При введении диэлектрика заряд остается неизменным (по условию задачи), т.е. q12 q . Напряжение на конденсаторе C1 равно
U1 q C0E0d E0d . C1 2C0 2
Тогда, напряженность электрического поля на конденсаторе C1
E1 U1 E0 . d 2
Аналогично рассуждая, получим E2 E0 .
Из граничных условий найдем D1 D2 0E1 0E0 .
III. Задачи для самостоятельного решения.
3.1. Точечный сторонний заряд q находится в центре диэлектрического шара радиуса a с проницаемостью 1. Шар окружен безграничным диэлектриком с проницаемостью 2. Найти поверхностную плотность связанных зарядов на границе раздела этих диэлектриков.
Ответ: |
q |
|
|
1 2 |
. |
|
2 |
|
|||
|
4 a |
|
|
||
|
|
1 2 |
|
||
3.2. Проводник произвольной формы, имеющий заряд q 2,5 мкКл, окружен одно-
родным диэлектриком с проницаемостью 5,0 (рис. 3.7). Найти суммарные поверхностные связанные заряды на внутренней и наружной поверхностях диэлектрика.
Ответ: qвнутр/ q 1 2 мкКл,
qнаруж/ q 1 2 мкКл.
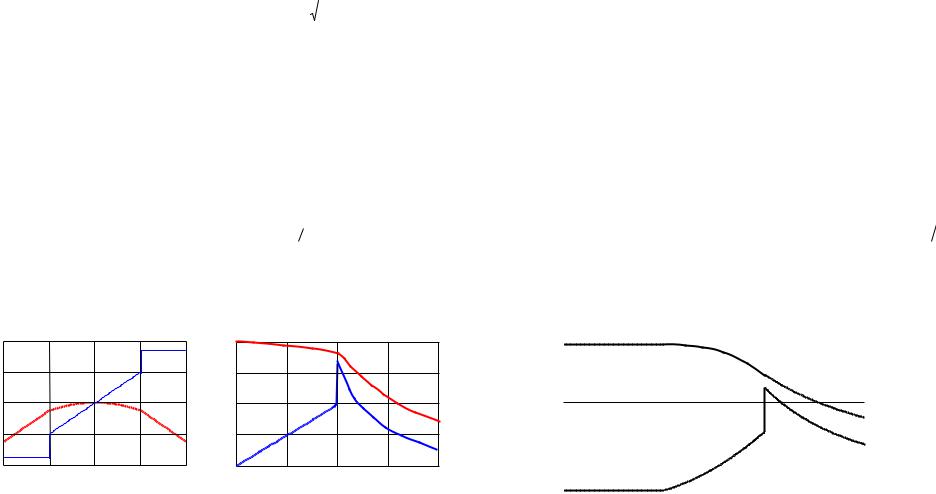
3.3 Вблизи точки A (рис. 3.8) границы раздела стекло-вакуум напряженность электри-
ческого поля в вакууме E0 10,0 В/м, причем угол между вектором E0 и нормалью n
к границе раздела 0 300 . Найти напряженность E поля в стекле вблизи точки A,
угол между векторами E0 и n , а также поверхностную плотность связанных зарядов в точке A.
|
|
E0 |
|
|
|
|
|
|
|
||
|
Ответ: E |
|
cos2 |
0 |
2 sin2 0 |
|
5,2 В/м, |
||||
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||
|
0, 740, |
|
|
1 |
|
|
пКл/м2. |
||||
tg tg |
0 |
|
|
E0 cos 0 |
64 |
||||||
|
|
||||||||||
3.4. Бесконечно большая пластина из однородного диэлектрика с проницаемостью заряжена равномерно сторонним зарядом с объемной плотностью . Толщина пластины 2d. Найти: а) модуль напряженности электрического поля и потенциал как функции расстояния l от середины пластины (потенциал в середине пластины положить равным нулю); взяв ось x перпендикулярно к пластине, изобразить примерные графики зависимостей проекции Ex(x) и потенциала (x); б) поверхностную и объемную плотности связанного заряда.
E l d |
l |
, |
E l d |
d |
; |
l d |
l2 |
, |
||||||
|
|
|
|
|
2 0 |
|||||||||
Ответ: а) |
0 |
|
|
0 |
|
|
||||||||
|
|
d 2 l d d |
|
|
|
|
||||||||
l d |
. |
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
0 |
|
|
|
|||||
б) d |
1 |
, |
|
1 |
. |
|
|
|
||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||
Графики зависимостей Ex(x) и (x)представлены на рис. 3.9.
E |
|
|
|
0 |
|
|
E |
|
|
- |
|
Рис. 3.9 |
Рис.3.10 |
3.5. Сторонние заряды равномерно распределены с объемной плотностью 0 по
шару радиуса R из однородного изотропного диэлектрика с проницаемостью . Найти: а) модуль напряженности электрического поля как функцию расстояния r от центра шара; изобразить примерные графики зависимостей E(r) и (r) ; б) объемную и поверхностную плотности связанных зарядов.
Ответ: а)E r R |
r |
, |
E r R |
R3 |
; |
|
3 0r2 |
||||
|
3 0 |
|
|
||
|
|
R |
2 |
2 1, |
r R 0 |
|
r |
2 |
|
1 |
|
|
|
r R |
|
R |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
0 |
|
|
1 |
R |
2 |
|
2 1 |
, |
|
|
. |
|||||||||
|
|
6 0 |
|
|
|
|
|
|
|
|
3 0r |
|||||||||
|
|
|
|
|
|
б) R |
1 |
, |
|
1 |
. |
|||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
Графики зависимостей E(r) и (r) представлены на рис. 3.10.
3.6. При некоторых условиях поляризованность безграничной незаряженной пластины
|
|
|
|
|
x |
2 |
|
|
из диэлектрика имеет вид |
P P |
|
1 |
|
, где P |
– вектор, перпендикулярный к пла- |
||
|
|
|||||||
|
|
0 |
|
|
d |
2 |
|
|
|
|
|
|
|
|
|
|
|
стине, x – расстояние от середины пластины, d – ее полутолщина. Найти напряженность электрического поля внутри пластины и разность потенциалов между ее поверхностями.
|
|
1 x |
2 |
d |
2 |
|
|
|
4P0d |
|
Ответ: E P |
|
|
, |
U |
. |
|||||
|
|
|
|
|
|
|||||
|
0 |
0 |
|
|
|
|
|
3 0 |
||
|
|
|
|
|
|
|
||||
3.7. Однородный диэлектрик имеет вид сферического слоя с радиусами a и b, причем a b. Изобразить примерные графики модуля напряженности электрического поля E и потенциала как функции расстояния r от центра системы, если диэлектрик имеет положительный сторонний заряд, распределенный равномерно по объему слоя.
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: Графики зави- |
||||
|
|
|
|
|
|
|
|
|
|
|
симостей E(r) и (r) пред- |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ставлены на рис. 3.11. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
3.8. Площадь пластин плос- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
кого воздушного конденса- |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
тора S 0.01 |
м2, расстоя- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
ние между ними d 5 мм. |
|||||
|
|
|
|
|
E |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
К |
пластинам |
|
приложена |
|||
|
|
|
|
|
|
|
|
|
|
|
|
разность |
|
|
потенциалов |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
|
|
|
|
|
|
|
|
|
|
|
U1 300 |
В. После отклю- |
||||
|
|
a |
|
b |
|
|
|
r |
|
чения конденсатора от ис- |
|||||||
|
|
Рис. 3.11 |
|
|
|
|
|
|
|
|
точника |
напряжения про- |
|||||
|
|
|
|
|
|
|
|
|
|
странство между пластина- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
ми |
заполняется эбонитом. |
||||
Какова будет разность потенциалов U2 |
между пластинами после заполнения? Найти |
||||||||||||||||
емкости конденсатора C1 |
и C2 , а также поверхностные плотности заряда 1 и 2 на |
||||||||||||||||
пластинах до и после заполнения. |
|
|
|
U1 1 |
|
|
|
|
0 1S |
|
|||||||
|
|
|
|
|
Ответ: U2 |
|
115В, C1 |
|
17,7 пФ, |
||||||||
|
|
|
|
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|

|
|
0 |
2S |
|
|
|
C1U1 |
2 |
C2 |
|
|
|
46 |
пФ, 1,2 |
|
|
531нКл/м . |
d |
|
S |
||||||
|
|
|
|
|
|
|
3.9. Решить предыдущую задачу для случая, когда заполнение пространства между пластинами изолятором производится при включенном источнике напряжения.
|
|
|
|
|
Ответ: C1 |
|
|
0 1S |
17,7 пФ, C |
2 |
|
0 2S |
|
46 пФ, |
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
d |
|
|
|
|
|
||||
|
|
|
|
|
1 |
0 1U |
531нКл/м2, 2 |
0 2U |
1,38 мкКл/м2. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
||||||
3.10. Площадь пластин плоского конденсатора S 0.01 |
м2, расстояние между ними |
||||||||||||||||||||||||||||
d 1 см. К пластинам приложена разность потенциалов |
U 300 |
|
В. В пространстве |
||||||||||||||||||||||||||
между |
пластинами |
находятся плоскопараллельная пластинка |
|
стекла |
толщиной |
||||||||||||||||||||||||
d1 0,5 |
см и плоскопараллельная пластинка парафина толщиной |
|
d2 0,5 |
см. Найти |
|||||||||||||||||||||||||
напряженности E1 |
и E2 электрического поля и падения потенциала U1 и U2 в каж- |
||||||||||||||||||||||||||||
дом слое. Каковы будут при этом емкость C конденсатора и поверхностная плотность |
|||||||||||||||||||||||||||||
заряда на пластинах? |
|
|
1 2S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
CU |
2 |
||||||||||||||||
|
|
|
|
|
Ответ: С |
|
|
|
|
|
|
26,6 |
пФ, |
|
|
|
|
0,8 мкКл/м . |
|||||||||||
|
|
|
|
|
|
|
d1 2 |
d2 1 |
|
|
|
S |
|
|
|
|
|
||||||||||||
3.11. Решить задачу 3.6 при условии, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
диэлектриком заполнили половину зазора, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||
как показано на рис.3.12. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
E E |
2 |
|
2E0 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ответ: 1 |
|
1 |
|
|
|
|
|
|
|
|
Рис. 3.12 |
|
|
|
|
|
|||||||||||||
|
D1 0E0, |
D2 D1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3.12. Половина пространства между двумя концентриче- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
скими обкладками сферического конденсатора заполне- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
на, как показано на рис. 3.13, однородным изотропным |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
диэлектриком с проницаемостью . Заряд конденсатора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
равен q. Найти модуль вектора напряженности электри- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
ческого поля между обкладками как функцию расстояния |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
r от центра кривизны этих обкладок. |
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
Ответ: E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
2 0 1 r2 |
|
|
Рис. 3.13 |
|
|
|
|
|
||||||||||||||||
3.13. Два одинаковых небольших одноименно заряженных шарика подвешены на изолирующих нитях равной длины к одной точке. При за-
полнении окружающей среды керосином угол расхождения нитей не изменился. Найти плотность материала шариков.
Ответ: кер кер .кер 1
3.14. Внутри шара из однородного изотропного диэлектрика с проницаемостью 5 создано однородное электрическое поле напряженности E 100 В/м. Радиус шара R 3 см. Найти максимальную поверхностную плотность связанных зарядов и полный связанный заряд одного знака.
Ответ: макс/ 1 0E 3,5нКл/м2, q R2 1 0E 10 пКл.
3.15. Точечный заряд q находится в вакууме на расстоянии l от плоской поверхности
однородного изотропного диэлектрика, заполняющего все полупространство. Проницаемость диэлектрика равна . Найти: а) поверхностную плотность связанных зарядов как функцию расстояния r от точечного заряда q; рассмотреть случай l 0; б) суммарный связанный заряд на поверхности диэлектрика.
Ответ: а) |
1 |
|
ql |
, при l 0 |
величина 0; б) q |
1 |
q. |
|
1 |
|
2 r3 |
|
|
1 |
|
3.16. Воспользовавшись условием и решением предыдущей задачи, найти модуль силы, действующей на заряд q со стороны связанных зарядов на поверхности диэлектрика.
Ответ: F |
1 |
q |
2 |
. |
|
|
|
|
|
||
|
116 0l2 |
||||
3.17. Точечный заряд q находится на плоскости, отделяющей вакуум от безграничного однородного изотропного диэлектрика с проницаемостью . Найти модули векторов
D и E , потенциал как функцию расстояния r от заряда q.
Ответ: в вакууме D |
|
|
q |
, |
в диэлектрике |
D |
|
q |
, |
||
2 1 r2 |
2 1 r2 |
||||||||||
всюду |
E |
q |
|
|
, |
q |
|
|
. |
|
|
2 0 1 r2 |
2 0 1 r |
|
|||||||||
3.18 Пластина толщины h из однородного статически поляризованного диэлектрика находится внутри плоского конденсатора, обкладки которого соединены между собой проводником. Поляризован- 
ность диэлектрика равна P (рис. 3.14). Расстояние между
обкладками конденсатора d .
Найти векторы D и E внутри и вне пластины.
Ph
Ответ: E1 0d (в зазоре),
|
|
|
|
|
|
|
|
|
|
|
|
d |
||
|
|
|
|
|
|
|
|
|
h |
|
||||
|
|
|
P |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Рис. 3.14 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
h P |
|
|
|
Ph |
|||||
|
E |
|
1 |
|
|
|
, D D |
|
|
. |
||||
|
|
|
|
|
||||||||||
|
|
2 |
|
|
d 0 |
1 |
2 |
|
d |
|||||

3.19. Длинный диэлектрический цилиндр круглого сечения поляризован так, что век-
тор P r , где - положительная постоянная, r - расстояние от оси. Найти объемную плотность связанных зарядов как функцию расстояния r от оси.
Ответ: 2 , т.е. от r не зависит. 3.20. Диэлектрический шар поляризован однородно и статически. Его поляризован-
ность равна P . Имея в виду, что так поляризованный шар можно представить как результат малого сдвига всех положительных зарядов диэлектрика относительно всех отрицательных зарядов, а) найти напряженность электрического поля внутри шара; б) показать, что поле вне шара является полем диполя, расположенного в центре шара, и
3
потенциал поля p0r 4 0r , где p0 - электрический момент шара, r - расстояние от его центра.
P
Ответ: E . 3 0
3.21. В однородное электрическое поле напряженности E0 поместили однородный диэлектрический шар. При этих условиях диэлектрик поляризуется однородно. Найти напряженность E электрического поля внутри шара и поляризованность P диэлектрика, проницаемость которого равна . При решении воспользоваться результатом предыдущей задачи.
|
3E0 |
|
|
2 0E0 1 |
|
Ответ: E |
|
, |
P |
|
. |
2 |
2 |
||||
3.22. Бесконечно длинный диэлектрический цилиндр круглого сечения поляризован
однородно и статически, причем поляризованность P перпендикулярна к оси цилиндра. Найти напряженность электрического поля в диэлектрике.
|
P |
|
|
Ответ: E |
. |
||
|
|||
|
2 0 |
||
3.23. Длинный цилиндр круглого сечения из однородного диэлектрика поместили в однородное электрическое поле в напряженностью E0 . Ось цилиндра перпендикуляр-
на к вектору E0 . При этих условиях диэлектрик поляризуется однородно. Воспользо-
вавшись результатом решения предыдущей задачи, найти напряженность электрического поля внутри цилиндра и поляризованность диэлектрика, проницаемость которого равна .
|
2E0 |
|
|
2 0E0 1 |
|
Ответ: E |
|
, |
P |
|
. |
1 |
1 |
||||
§4. Закон Био-Савара-Лапласа. Теорема о циркуляции.
I. Краткие теоретические сведения
Магнитное поле В, создаваемое точечным зарядом q, движущимся со скоростью v, в некоторой точке:
|
0 |
|
q[vr] |
|
B |
|
, |
||
4 |
|
r3 |
||
|
|
|
где r – радиус – вектор, проведенный от заряда к точке, в которой определяется поле. Результат векторного произведения – вектор В направлен перпендикулярно плоскости, в которой лежат вектор скорости и радиус - вектор, причем вектора r, v и B должны образовывать правую тройку.
Закон Био-Савара-Лапласа для проводника с током I, элемент которого dl создает в некоторой точке поле, индукция которого dB, записывается в виде:
|
0 |
|
I dlr |
|
dB |
|
|
|
, |
4 |
|
|||
|
|
r3 |
||
где dl – вектор по модулю равный длине элемента dl и совпадающий по направлению с током, r – радиус – вектор, проведенный из элемента dl в точку, в которой определяется поле. Направление вектора dB перпендикулярно dl и r, т.е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции.
0 = 4 10-7 = 1.257 10-6 Гн/м – магнитная постоянная.
Теорема о циркуляции вектора В: циркуляция вектора В по замкнутому произвольному контуру равна произведению магнитной постоянной 0 на алгебраическую сумму токов, охватываемых этим контуром:
|
|
N |
Bdl |
0 Ik , |
|
L |
|
k 1 |
где N – число проводников с токами, охватываемых контуром L произвольной формы. Магнитное поле в центре кругового витка с током I:
B 0 I ,
2R
где R – радиус витка.
Поле на оси кругового витка с током I:
B |
0 |
|
I R2 |
|
, |
|
|
R2 z2 3 |
|
||
2 |
|
2 |
|
||
где R – радиус витка, z – расстояние от центра витка то дочки, в которой определяется поле.
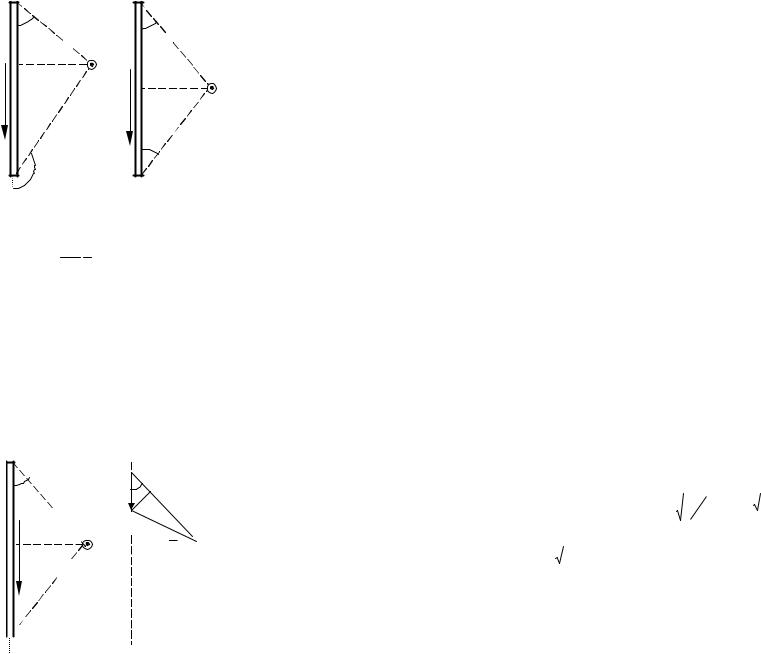
Поле бесконечно длинного проводника с током I:
B 0 I , 2 x
где x – расстояние от оси проводника то дочки, в которой определяется поле.
1 |
В |
|
|
|
|
|
|
|
|
х |
|
х |
В |
|
I |
|
|
||
|
I |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
Рис.4.1 |
|
|
|
Поле отрезка проводника с током I: |
|
|
|
|
B 0 |
I cos cos |
2 |
, |
|
4 |
x |
1 |
|
|
|
|
|
||
где x – расстояние от оси проводника то дочки, в которой определяется поле, углы 1 и2 – указаны на рисунке.
Если проводник расположен симметрично относительно точки наблюдения, то:
B |
0 |
|
I |
cos , |
2 |
|
|||
|
|
x |
||
где угол указан на рис. 4.1.
II. Примеры решения задач
Пример 4.1. Определить индукцию магнитного поля, создаваемого отрезком проводника длиной l в точке, отстоящей на расстоянии х от центра проводника.
|
|
1 |
dl С |
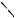 А
А
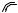 r х
r х 

 d
d 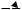
I 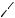 В
В
 2
2
Рис. 4.2
Решение.
На проводнике выбираем элемент тока длиной dl. По закону Био-Савара магнитное поле создаваемое этим элементом с током равно:
|
|
|
|
|
|
|
|
0 |
I dlr sin |
0 |
|
I dlsin |
||||||||
|
|
|
dB |
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||
4 |
|
|
|
|
|
4 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
r3 |
|
r2 |
|||||||||
где - угол между векторами dl и r. |
|
|
|
|
||||||||||||||||
Из рис. 4.2 видно, что sin |
|
AC |
, |
dl |
|
AC |
. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
dl |
|
|
sin |
|
|
|
|
||||||
С другой стороны d |
AC |
, AC r d . |
|
|
|
|
||||||||||||||
|
|
|
|
|
||||||||||||||||
|
r d |
|
r |
|
|
|
|
|
|
|
|
|
|
|||||||
Тогда dl |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
sin |
|
|
|
|
|
|
|
|
|
|
|||||||||
Можно записать, чтоsin |
х |
, r |
|
х |
. |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
r |
|
sin |
|
|
|
|
|||||||||
Тогда dl |
хd |
. |
|
||
|
sin2 |
|
Закон Био-Савара можно записать как:
|
0 |
I sin |
|
хd |
0 |
|
I |
||||||
dB |
|
|
|
|
|
|
|
|
|
|
|
|
sin d . |
4 |
х 2 |
|
sin2 |
|
|
|
|||||||
|
|
|
4 х |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
sin
Магнитное поле всего проводника:
B 1 |
0 |
|
I |
sin d |
0 |
|
I |
cos |
cos |
||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
4 х |
|
4 х |
|
1 |
1 |
|
||||||||||||||||||||
|
|
|
|
|
|
. |
|
||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
0 |
|
I |
cos cos |
0 |
|
|
I |
|
2cos |
|
|
|
|
|||||||||||||||
4 х |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
1 |
|
1 |
|
4 х |
|
1 |
|
|
|
|
|
||||||||||||||||
B |
0 I |
cos 1, cos |
l |
|
|
|
|
|
|
|
|
l |
|
|
|
|
l |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 х |
2r |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
2 l2 |
4 |
x2 |
l2 4x2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
0 I |
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
l2 4x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Пример 4.2. Определить индукцию магнитного поля проводника с током, имеющего форму дуги окружности радиуса R.
Решение.
Выбираем на окружности элемент длиной dl, проводим радиус-вектор r, соединяющий данный элемент с точкой, в которой необходимо определить поле (рис.4.3). Угол между векторами равен 90 . Тогда закон Био-Савара можно записать в виде:

dB |
0I |
|
dl r sin90 |
|
0I |
|
dl |
|
0I |
|
Rd |
|
0I |
|
d |
, |
4 |
|
r3 |
4 r2 |
4 R2 |
|
|
||||||||||
|
|
|
|
|
4 R |
|||||||||||
d - угол, под которым из точки наблюдения виден элемент dl. По принципу суперпозиции просуммируем все поля создаваемые такими элементами:
|
|
|
0I |
0I |
|
|
|
|
B dB 4 R d 4 R . |
|
|
||
|
|
0 |
|
|
|
|
|
dl |
d |
I |
1 |
a |
O |
|
|
|
|
|
B |
|
I |
r |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
R |
B |
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.3 Рис. 4.4
Пример 4.3. Определить индукцию магнитного поля в точке О для проводника, показанного на рисунке, если по проводнику течет ток I.
Решение.
Разобьем проводник на два участка 1 и 2 (рис.4.4) и воспользуемся принципом супер-
позиции: В В1 В2 . Магнитное поле, создаваемое первым проводником равно нулю
т.к. угол между векторами dl и r равен нулю и dlr 0 , магнитное поле второго проводника:
B2 0 I В. 4 a
III. Задачи для самостоятельного решения.
4.1. По круговому витку радиуса R = 100 мм из тонкого провода циркулирует ток I =1,00 А. Найти индукцию магнитного поля в центре витка.
Ответ: В = 6,3 мкТл. 4.2. По круговому витку радиуса R = 100 мм из тонкого провода циркулирует ток I =1,00 А. Найти индукцию магнитного поля на оси витка в точке, отстоящей от его центра на х = 100 мм.
Ответ: В = 2,3 мкТл. 4.3. Определить магнитную индукцию в точке О, если проводник с током I имеет вид, показанный на рис.4.5. Геометрические размеры и направление тока показаны на рисунке.
Ответ: В |
|
0 |
I |
2 |
||
|
|
1 |
|
|
||
4R |
|
|||||
|
|
|
||||
4.4. Определить магнитную индукцию в точке О, если проводник с током I имеет вид, показанный на рис.4.6. Геометрические размеры и направление тока показаны на рисунке.
Ответ: В |
|
0 |
I |
3 |
|
1 |
||
|
|
|
|
|
|
|||
4R |
|
|
||||||
|
2 |
|
||||||
4.5. Определить магнитную индукцию в точке О, если проводник с током I имеет вид, показанный на рис.4.7. Геометрические размеры и направление тока показаны на рисунке.
Ответ: В 0I 2
4 R
4.6. Определить магнитную индукцию в точке О, если проводник с током I имеет вид, показанный на рис.4.8. Геометрические размеры и направление тока показаны на рисунке.
Ответ: В |
|
0 |
I |
1 |
||
|
|
1 |
|
|
||
2R |
|
|||||
|
|
|
||||
4.7. Определить магнитную индукцию в точке О, если проводник с током I имеет вид, показанный на рис.4.9. Геометрические размеры и направление тока показаны на рисунке.
Ответ: В 0I
4 R
4.8. Определить магнитную индукцию в точке О, если проводник с током I имеет вид, показанный на рис.4.10. Геометрические размеры и направление тока показаны на рисунке.
Ответ: В 0I 2
4 R
4.9. Определить магнитную индукцию в точке О, если проводник с током I имеет вид, показанный на рис.4.11. Геометрические размеры и направление тока показаны на рисунке.
Ответ: В 0I
4R
4.10. Определить магнитную индукцию в точке О, если проводник с током I имеет вид, показанный на рис.4.12. Геометрические размеры и направление тока показаны на рисунке.
Ответ: В |
|
0 |
I 2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
4 |
а |
а |
|
|||||||
|
|
|
|
b |
||||||
4.11. Определить магнитную индукцию в точке О, если проводник с током I имеет вид, показанный на рис.4.13. Геометрические размеры и направление тока показаны на рисунке.
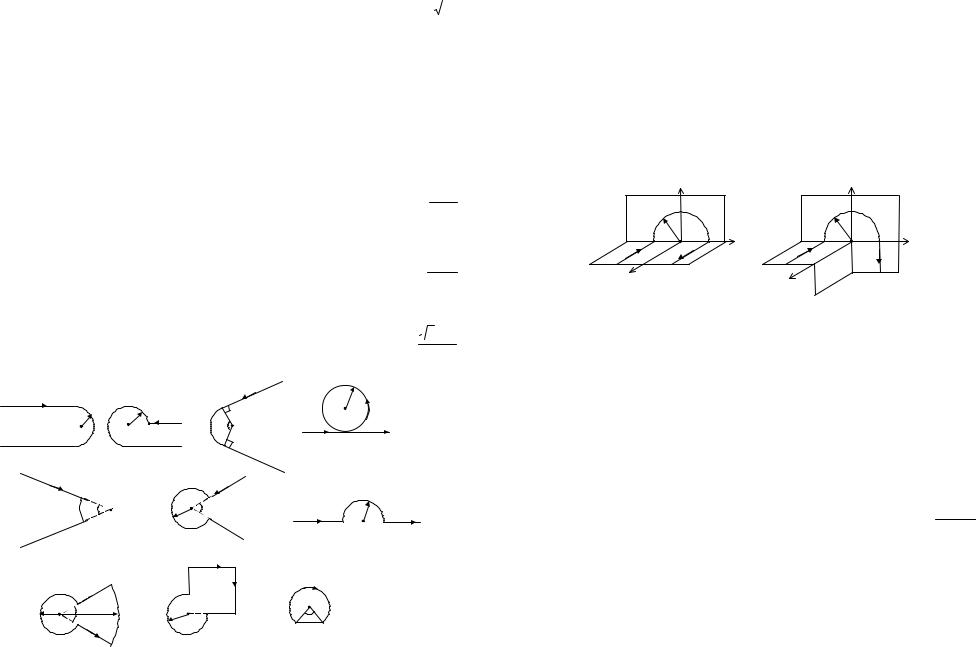
|
|
0 |
I |
3 |
|
|
2 |
|
|
|
Ответ: В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4 |
|
|
2а |
|
b |
|
||||
|
|
|
|
|||||||
4.12. Определить магнитную индукцию в точке О, если проводник с током I =5 А имеет вид, показанный на рис.4.14. Геометрические размеры и направление тока показаны на рисунке, угол 2 = 90 , радиус изогнутой части проводника 120 мм.
Ответ: В = 28 мкТл 4.13. Найти индукцию магнитного поля в центре контура, имеющего вид прямоугольника с диагоналями 16 см, угол между диагоналями 30 и ток в контуре 5 А.
Ответ: В = 0.1 мТл. 4.14. Найти индукцию магнитного поля в центре контура, имеющего вид квадрата, если его диагональ равна d и ток в контуре I.
Ответ: В 4 0I
d
4.15. Определть индукцию магнитного поля в центре равностороннего треугольника со стороной а, обтекаемого током I.
Ответ: В 9 0I
2 a
4.16. Определить индукцию магнитного поля в центре правильного шестиугольника со стороной а, обтекаемого током I.
Ответ: В  3 0I
3 0I
a
I |
|
R |
|
|
I |
|
R |
R |
|
I |
|
O |
|
O |
|
O |
O |
|
|
|
|||
|
|
|
|
||||
|
|
|
R |
|
I |
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Рис. 4.5 |
|
Рис.4.6 |
|
Рис.4.7 |
|
Рис.4.8 |
|
|
|
|
|
|
|
||
I |
|
|
|
I |
|
|
|
R |
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
O |
|
|
I |
R |
||
|
R |
|
|
||||
|
|
|
|
|
O |
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Рис.4.9 |
|
|
Рис.4.10 |
|
|
Рис.4.11 |
|
|
|
|
b |
I |
I |
|
|
|
|
|
|||
O |
|
b |
O |
|
O |
|
b |
R 2 |
|||||
a |
|
|
a |
|||
|
I |
|
|
|
||
|
|
|
|
Рис.4.14 |
||
Рис.4.12 |
|
Рис.4.13 |
|
|||
|
|
|
||||
4.17. Длинный проводник с током 5 А изогнут под прямым углом. Найти магнитную индукцию в точке, которая отстоит от плоскости проводника на расстояние 35 см и находится на перпендикуляре к проводникам, проходящем через точку изгиба.
Ответ: В = 2 мкТл. 4.18. Ток в 20 А идет по длинному проводу, согнутому под прямым углом. Найти индукцию магнитного поля в точке, лежащей на биссектрисе угла и отстоящей от его вершины на расстояние 10 см.
Ответ: В = 97 мкТл. 4.19. Найти магнитную индукцию в точке О, если проводник с током I = 8 А имеет вид, показанный на рис. 4.15. Радиус изогнутой части проводника R = 100 мм, прямолинейные участки проводника очень длинные.
Ответ: В = 30 мкТл
y |
y |
R |
O |
R |
O |
z |
z |
x |
x |
|
Рис.4.15
Рис.4.16
4.20. Найти магнитную индукцию в точке О, если проводник с током I = 8 А имеет вид, показанный на рис. 4.16. Радиус изогнутой части проводника R = 100 мм, прямолинейные участки проводника очень длинные.
Ответ: В = мкТл 4.21. Однородный ток плотности j течет внутри неограниченной пластины толщины 2d параллельно ее поверхности. Найти индукцию магнитного поля этого тока, как функ-
цию расстояния х от средней плоскости пластины. |
|
Ответ: B 0 jx x d, |
B 0 jd x d |
4.22. Найти плотность тока как функцию расстояния r от оси аксиальносимметричного параллельного потока электронов, если индукция магнитного поля
внутри потока зависит от r как В br , где b и - положительные постоянные.
Ответ: B b 1 r 1 .
0
4.23. Внутри однородного длинного прямого провода круглого сечения имеется круглая длинная цилиндрическая полость, ось которой параллельна оси провода и смещена относительно последней на расстояние l. По проводу течет постоянны ток плотности j. Найти индукцию магнитного поля внутри полости.
|
0 |
|
|
|
Ответ: B |
j,l |
|
||
2 |
||||
|
|
|
