
К решению задач по электричеству
.pdf
4.24. Непроводящий тонкий диск радиуса R, равномерно заряжен с одной стороны с поверхностной плотностью , вращается вокруг своей оси с угловой скоростью . Найти индукцию магнитного поля в центре диска.
Ответ: В 0 R
2
4.25. По однородному прямому проводу, радиус сечения которого R, течет постоянный ток плотности j. Найти индукцию магнитного поля этого тока в точке, положение которой относительно оси провода определяется радиус – вектором r.
|
0 |
|
|
0R |
2 |
|
Ответ: B |
j,r r R, B |
|
j,r r R |
|||
2 |
2r2 |
|
||||
|
|
|
|
|
||
4.26. Тонкий провод (с изоляцией) образует плоскую спираль из N плотно расположенных витков, по которым течет ток I. Радиусы внутреннего и внешнего витков а и b. Найти индукцию магнитного поля в центре спирали.
Ответ: B |
0N I |
ln |
b |
2 b a |
a |
4.27. Определить индукцию магнитного поля тока, равномерно распределенного по плоскости с линейной плотностью j.
Ответ: B 0 j
2
4.28. Определить индукцию магнитного поля тока, равномерно распределенного по двум параллельным плоскостям с линейными плотностями j и –j.
B 0 j (между пластинами)
Ответ:
В 0 (вне пластин)
§5. Закон электромагнитной индукции.
I. Краткие теоретические сведения
Закон электромагнитной индукции Фарадея: ЭДС индукции, возникающая в замкнутом контуре, численно равна изменению магнитного потока в единицу времени. Направление ЭДС индукции таково, что индукционный ток создает магнитный поток, препятствующий изменению магнитного потока, вызывающего ЭДС индукции.
dФ . d t
Поток вектора магнитной индукции:
Ф B,S B S cos ,
где - угол между вектором магнитной индукции и нормалью к плоскости контура. Индуктивность соленоида:
L 0n2V ,
где - магнитная проницаемость материала сердечника, n – число витков на единицу длины, V – объем соленоида.
II. Примеры решения задач
Пример 5.1. Короткозамкнутый виток провода сопротивлением R, имеющий форму квадрата со стороной а, поместили в однородное магнитное поле с индукцией В, перпендикулярной плоскости витка. Затем витку придали форму половины окружности (не растягивая провод, а только деформируя его). Какой заряд протечет через поперечное сечение провода в результате такой деформации.
Решение. Из закона электромагнитной индукции:
dФ , d t
где магнитный поток Ф В,S BS cos BS , т.к. магнитное поле перпендикуляр-
но плоскости витка, т.е. угол между вектором магнитной индукции и нормалью к плоскости витка равен нулю.
Из закона Ома I R dq R , d t
где R – сопротивление контура. Тогда:
R |
dq |
|
dФ |
, dq |
1 |
dФ |
|
|
||||
|
dt |
|
|
|
||||||||
|
dt |
|
|
|
R |
|
|
|||||
1 |
|
ФК |
1 |
|
ФК ФН |
B |
SН SК |
|||||
q |
|
|
dФ |
|
|
|
||||||
R |
R |
R |
||||||||||
ФН
Начальная площадь контура: SH a2 , конечная площадь контура – площадь половины
окружности: |
SR |
|
r |
2 |
, где r – радиус окружности. Радиус окружности найдем из |
|
|
||||
|
|
2 |
|
|
|
условия, что длина провода остается неизменной: 4а r 2r, r 4a . Тогда ко- 2
нечная площадь контура:S |
|
|
|
|
4a |
|
2 |
8 a |
2 |
. |
K |
|
|
|
|
|
|
|
|
||
|
|
|
|
|||||||
|
|
2 2 |
|
2 2 |
||||||
Таким образом, заряд который пройдет через поперечное сечение провода:
|
B |
|
|
8 a2 |
|
|
|
Ba2 |
8 |
|
|
|
q |
|
a2 |
|
|
|
|
|
|
1 |
|
|
. |
|
|
2 |
|
|
2 |
|||||||
|
R |
|
|
2 |
|
|
R |
|
2 |
|
||
|
|
|
|
|
|
|
|
|
||||
Пример 5.2. Кольцо радиуса r вращается вокруг оси лежащей в его плоскости, так что угловая скорость зависит от времени по закону аt (где а > 0). Кольцо помещено
в однородное магнитное поле с индукцией В, направленной перпендикулярно к оси вращения. Найти индукционный ток в кольце, если его сопротивление R.
Решение.
Индукционный ток :
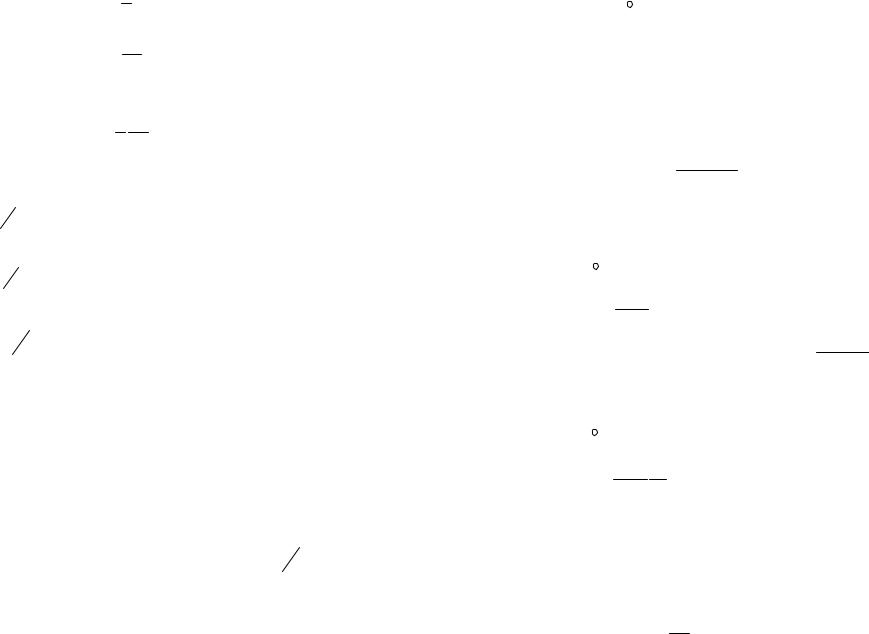
I .
R
Из закона электромагнитной индукции:
dФ , d t
где магнитный поток Ф В,S BS cos , - угол между вектором магнитной индукции и нормалью к плоскости контура. Тогда:
I 1 dФ . R dt
Вначальный момент времени нормаль к контуру совпадает с направлением вектора индукции магнитного поля:
ФВ,S BS cos BS .
Вмомент времени t T 4, (где Т – период вращения, т.е. время одного полного оборо-
та) кольцо повернется на угол 90 вокруг своей оси, т.е. = 90 и магнитный поток равен нулю.
В момент времени t T 2, кольцо повернется на угол 180 вокруг своей оси, т.е. = 180 и магнитный поток равен:
ФВS cos 180 ВS .
Вмомент времени t 3T 4 , кольцо повернется на угол 270 вокруг своей оси и =
270 , т.е. магнитный поток равен нулю. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Таким образом, |
зависимость |
|
магнитного потока |
от |
|
времени имеет |
|||||||||||||
вид:Ф(t) BS cos t , где |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Магнитный поток: |
Ф(t) B r |
2 |
cosat |
2 |
и |
|
dФ |
B r |
2 |
2atsin at |
2 |
. Тогда индукцион- |
|||||||
|
|
|
dt |
|
|
||||||||||||||
ный ток равен: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 B |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
I |
|
r |
2 |
sin t . |
|
|
|
|
|
|
|
|||||
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 5.3. В очень длинном соленоиде, радиус которого равен R, а число витков на |
|||||||||||||||||||
единицу длины равно n, ток изменяется со временем по закону: |
I(t) I0t |
|
(где I0 и - |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
положительные постоянные). Определит напряженность электрического вихревого поля Е(r) (внутри и снаружи соленоида) в любой момент времени.
Решение.
Закон электромагнитной индукции:
|
|
dФ |
|
Edl |
|
|
, |
dt |
L
где Ф BS - поток вектора магнитной индукции. Индукция магнитного поля внутри
соленоида: В 0nI , индукция магнитного поля вне бесконечного соленоида равна
нулю. Силовые линии магнитного поля параллельны оси соленоида, силовые линии электрического поля – окружности, плоскости которых перпендикулярны оси соленоида. Выбираем замкнутый контур вдоль силовой линии электрического поля внутри соленоида, тогда поток вектора магнитной индукции через поверхность ограниченную данным контуром равен:
Ф 0n I r2 0n I0 r2 t ,
где r – радиус замкнутого контура.
|
dФ |
|
0n I0 r2 |
. |
|
|
dt |
|
|||
|
|
|
|
|
|
|
|
|
|
0nI0 r2 |
|
Edl 2E r |
|
||||
|
|||||
L
E 0nI0 r, r R
2
Если замкнутый контур выбираем вне соленоида, то Ф 0n I R2 0n I0 R2 t .
|
dФ |
|
0n I0 R2 |
|
|
|
dt |
|
|||
|
|
||||
|
|
|
|
0nI0 R2 |
|
Edl 2E r |
|
||||
|
|||||
L
E 0nI0 R2 , r R
2 r
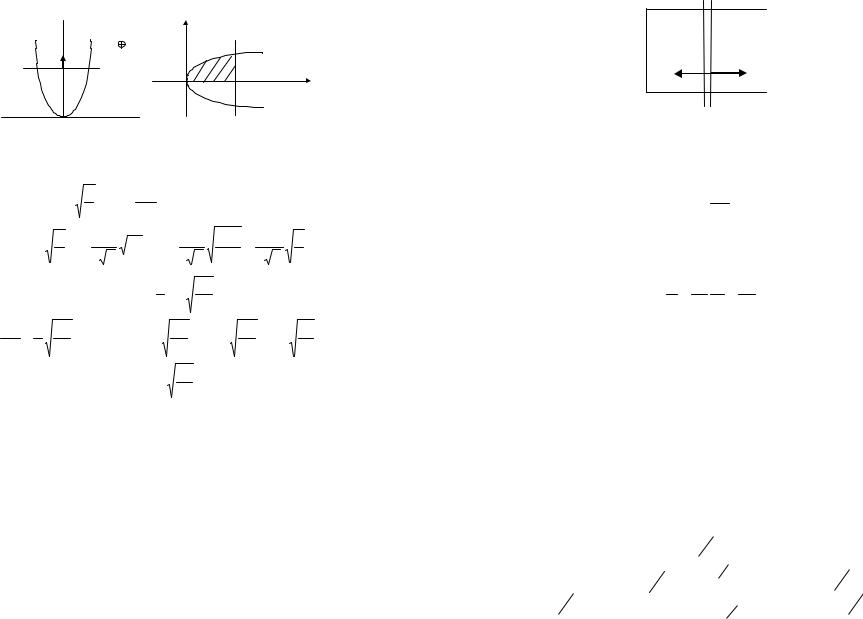
Пример 5.4. Провод, имеющий форму параболы y kx2 , находится в однородном
магнитном поле с индукцией В. Из вершины параболы в момент времени t = 0 начали перемещать перемычку 12 (рис. 5.1 а). Найти э.д.с. в образовавшемся контуре как функцию у, если перемычку перемещают с постоянным ускорением а, причем в момент t = 0 скорость перемычки была равна нулю.
Решение. Из закона электромагнитной индукции:
dФ ,
d t
где магнитный поток Ф В,S BScos BS , = 0 - угол между вектором магнитной индукции и нормалью к плоскости контура.
|
y |
|
B |
|
|
|
|
х |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
O |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис 5.1 а |
|
|
|
|
|
|
|
|
Рис. 5.1 б |
|
|
||
Чтобы найти площадь |
S, |
вычислим |
|
|
площадь |
заштрихованной фигуры S/ на |
|||||||
рис. 5.1 б, учитывая, что x |
y |
at |
2 |
. |
|
|
|
|
|
|
|||
и |
y |
|
2 |
|
|
|
|
|
|
|
|||
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
y |
y |
2 |
|
|
|
|
|
|
|
2 |
a3t6 |
|
2at3 a |
S/ |
y3 , |
S/ |
|
|
|
||||||||
k dy |
3 k |
|
|
3 k |
8 |
|
6 k 2 . |
||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S 2S |
/ |
|
2 |
at |
3 a |
. |
|
|
|||
|
|
|
3 |
2k |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
dФ 2 |
a aB 3t2 2Bat2 |
|
a 4 yB |
a yB 8a . |
|||||||||
dt 3 |
2k |
|
|
|
|
|
|
2k |
|
2k |
k |
||
|
|
|
B y |
|
8a . |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
Пример 5.5. По П-образному проводнику, расположенному в горизонтальной плоскости, может скользить без трения перемычка 12 (рис. 5.2). Перемычка имеет длину l, массу m и сопротивление R. Вся система находится в однородном магнитном поле с индукцией В. В момент времени t = 0 на перемычку стали действовать постоянной горизонтальной силой F, и перемычка начала перемещаться вправо. Найти зависимость от времени скорости перемычки. Самоиндукция и сопротивление П-образного проводника малы.
2  dx
dx
В 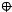
 I n
I n  F
F
FА
1
Рис. 5.2
Решение.
При перемещении перемычки под действием силы F в контуре возникает ЭДС индукции и индукционный ток (направление тока указано на рис. 5.2):
dФ , d t
где магнитный поток dФ BdScos BdS Вldx, = 180 - угол между вектором
магнитной индукции и нормалью к плоскости контура. Величина индукционного тока определяется выражением:
I Bl dx Bl v, R R dt R
где v – скорость движения перемычки.
На проводник, по которому течет ток, в магнитном поле действует сила Ампера:
FA Il B.
Уравнение движения перемычки имеет вид:
F F m |
dv |
, |
F Il B m |
dv |
, |
|
|
|||||||
|
|
|
|
|
||||||||||
A |
|
|
dt |
|
|
|
|
|
|
dt |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
F l B |
Bl |
v m |
dv |
, |
F |
|
l B 2 |
v |
dv |
, |
||||
|
|
|
|
|
||||||||||
|
R |
|
dt |
m Rm |
dt |
|||||||||
F |
av |
dv |
, |
a |
l B 2 |
m |
|
Rm |
|||
|
dt |
|
|||
Решаем дифференциальное уравнение:
|
|
|
|
|
|
|
dt |
|
|
dv |
|
|
||
|
|
|
|
|
|
|
F |
m |
av |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
v |
|
|
|
F |
|
|
|
|
F |
a v |
|||
|
d v |
|
|
|
|
m |
|
|
||||||
t |
|
|
y |
|
m |
av |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
F |
|
av |
|
|
|
|
||||||||
|
m |
|
|
|
|
|
|
|
||||||
|
0 |
|
|
dy adv |
|
|
|
F |
m |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
1 |
|
F |
m |
av |
|
|
dy |
ln |
|
|
. |
|||
a |
|
|
F |
|
||||
|
|
a |
m |
|||||
|
|
|
|
|
|
|
||

at ln |
F |
m |
av |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
F |
m |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
exp at |
|
F m av |
, |
F |
exp at |
F |
av |
|||||||||
|
|
|
m |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
F |
|
|
m |
|||
|
|
F |
|
|
F |
|
m |
|
|
|
|
|
||||
av |
|
exp at , |
|
|
|
|
||||||||||
m |
|
|
|
|
|
|||||||||||
|
|
|
|
m |
|
|
|
|
|
|
|
|||||
v |
F |
|
1 exp at |
|
|
|
|
|||||||||
am |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
III. Задачи для самостоятельного решения.
5.1. Короткозамкнутый виток провода сопротивлением R, имеющий форму квадрата со стороной а, поместили в однородное магнитное поле с индукцией В, перпендикулярной плоскости витка. Затем витку придали форму окружности (не растягивая провод, а только деформируя его). Какой заряд протечет через поперечное сечение провода в результате такой деформации.
|
B a2 |
|
4 |
|
Ответ: q |
|
1 |
|
. |
R |
|
|||
|
|
|
||
5.2. Короткозамкнутый виток провода сопротивлением R, имеющий форму равностороннего треугольника стороной а, поместили в однородное магнитное поле с индукцией В, перпендикулярной плоскости витка. Затем витку придали форму квадрата (не растягивая провод, а только деформируя его). Какой заряд протечет через поперечное сечение провода в результате такой деформации.
Ответ: q Ba2 4
 3 9 . 16R
3 9 . 16R
5.3. Короткозамкнутый виток провода сопротивлением R, имеющий форму правильного шестиугольника со стороной а, поместили в однородное магнитное поле с индукцией В, перпендикулярной плоскости витка. Затем витку придали форму квадрата (не растягивая провод, а только деформируя его). Какой заряд протечет через поперечное сечение провода в результате такой деформации.
|
3B a2 |
|
|
3 |
|
||
Ответ: q |
|
ctg |
|
|
|
. |
|
2R |
6 |
2 |
|||||
|
|
|
|
||||
5.4. Короткозамкнутый виток провода сопротивлением R, имеющий форму окружности радиуса а, поместили в однородное магнитное поле с индукцией В, перпендикулярной плоскости витка. Затем витку придали форму шестиугольника (не растягивая провод, а только деформируя его). Какой заряд протечет через поперечное сечение провода в результате такой деформации.
|
Ba2 |
|
|
|
|||
Ответ: q |
|
|
1 |
|
ctg |
|
. |
R |
|
6 |
|
||||
|
|
|
|
6 |
|||
5.5. Короткозамкнутый виток провода сопротивлением R, имеющий форму окружности радиуса а, поместили в однородное магнитное поле с индукцией В, перпендикулярной плоскости витка. Затем витку придали форму половины окружности большего радиуса (не растягивая провод, а только деформируя его). Какой заряд протечет через поперечное сечение провода в результате такой деформации.
|
Ba2 |
2 |
|
|
|
Ответ: q |
|
1 |
|
|
. |
|
|
2 |
|||
|
R |
|
2 |
|
|
|
|
|
|
||
5.6. Кольцо радиуса r вращается вокруг оси лежащей в его плоскости, так что угловая скорость зависит от времени по закону 0 аt2 (где 0 и а > 0). Кольцо помещено
в однородное магнитное поле с индукцией В, направленной перпендикулярно к оси вращения. Найти индукционный ток в кольце, если его сопротивление R.
Ответ: I 0 3at2 В r2 sin t R
5.7. В очень длинном соленоиде, радиус которого равен R, а число витков на единицу длины равно n, ток изменяется со временем по закону: I(t) I0 t 2 (где I0 и - по-
ложительные постоянные). Определит напряженность электрического вихревого поля Е(r) (внутри и снаружи соленоида) в любой момент времени.
|
Е |
0nI0 |
tr, r R |
||||
Ответ: |
2 |
||||||
|
|
|
|
|
|||
|
0nI0 |
|
R2 |
|
|
||
|
Е |
|
t, |
r R |
|||
|
2 |
|
|||||
|
|
|
r |
|
|||
5.8. В очень длинном соленоиде, радиус которого равен R, а число витков на единицу |
|||||||
длины равно n, ток изменяется со временем по закону: I(t) I0 sin t |
(где I0 |
и - |
|||||
положительные постоянные). Определит напряженность электрического вихревого поля Е(r) (внутри и снаружи соленоида) в любой момент времени.
Е |
0nI0 |
rcos t |
|
, |
r R |
|||
|
||||||||
Ответ: |
|
R2 |
cos t |
, |
|
|||
Е |
0nI0 |
|
r R |
|||||
|
|
r |
||||||
|
|
|
|
|
|
|
||
5.9. В очень длинном соленоиде, радиус которого равен R, а число витков на единицу |
||||||||
длины равно n, ток изменяется со временем по закону: I(t) I0 cos t (где I0 |
и - |
|||||||
положительные постоянные). Определит напряженность электрического вихревого поля Е(r) (внутри и снаружи соленоида) в любой момент времени.
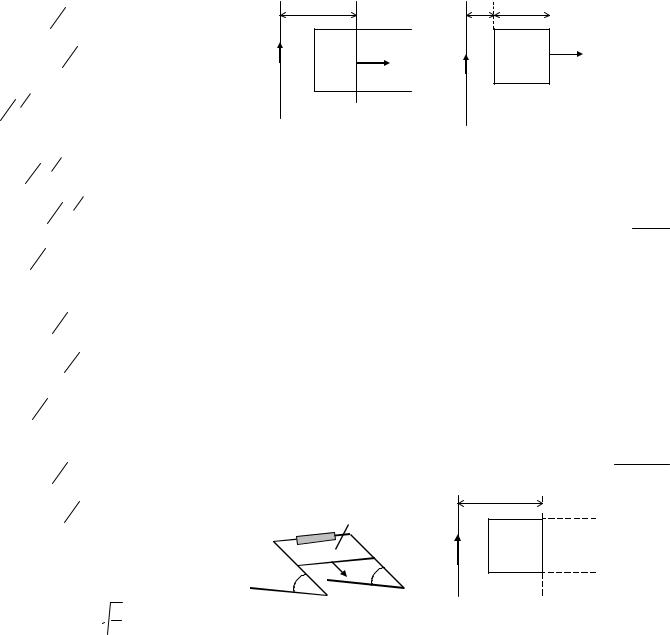
Е |
0nI0 |
rsin t |
|
, |
r R |
||
|
|||||||
Ответ: |
|
R2 |
sin t |
, r R |
|||
Е |
0nI0 |
|
|||||
|
|
r |
|||||
|
|
|
|
|
|
||
5.10. В очень длинном соленоиде, радиус которого равен R, а число витков на единицу
1
длины равно n, ток изменяется со временем по закону: I(t) I0 t 2 (где I0 и - по-
ложительные постоянные). Определит напряженность электрического вихревого поля Е(r) (внутри и снаружи соленоида) в любой момент времени.
|
|
0nI |
0 |
|
|
|
1 |
|
|
|
|
|
Е |
t |
|
|
2 r, r R |
||||||
Ответ: |
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|||
|
0nI |
|
|
R |
2 |
|
|
|
1 |
|
|
|
|
0 |
|
|
|
|
|||||
|
Е |
|
|
t |
|
|
2, |
r R |
|||
|
2 |
|
r |
||||||||
5.11. В очень длинном соленоиде, радиус которого равен R, а число витков на единицу |
|||||||||||
длины равно n, ток изменяется со временем по закону: I(t) I0 sin2 t |
(где I0 |
и - |
|||||||||
положительные постоянные). Определит напряженность электрического вихревого поля Е(r) (внутри и снаружи соленоида) в любой момент времени.
Е |
0nI0 |
rsin2 t |
|
, |
r R |
||
|
|||||||
Ответ: |
|
R2 |
sin2 t |
r R |
|||
Е |
0nI0 |
|
|||||
|
|
r |
|||||
|
|
|
|
|
|
||
5.12. В очень длинном соленоиде, радиус которого равен R, а число витков на единицу |
|||||||
длины равно n, ток изменяется со временем по закону: I(t) I0 cos2 t |
(где I0 и - |
||||||
положительные постоянные). Определит напряженность электрического вихревого поля Е(r) (внутри и снаружи соленоида) в любой момент времени.
Е |
0nI0 |
rsin2 t |
|
, |
r R |
||
|
|||||||
Ответ: |
|
R2 |
sin2 t |
, r R |
|||
Е |
0nI0 |
|
|||||
|
|
r |
|||||
|
|
|
|
|
|
||
5.13. Провод, имеющий форму параболы y kx2 , находится в однородном магнитном
поле с индукцией В. Из вершины параболы в момент времени t = 0 начали перемещать перемычку 12 (рис..5.1). Найти э.д.с. в образовавшемся контуре как функцию у, если перемычку перемещают с постоянной скоростью v.
Ответ: 2Bv
y
 k
k
r |
х |
a |
I |
v |
v |
|
||
|
I |
|
Рис 5.3 |
|
Рис 5.4 |
5.14. Длинный прямой проводник с током и П-образный проводник с подвижной перемычкой расположены в одной плоскости (рис 5.3). Перемычку. Длина которой l перемещают вправо с постоянной скоростью v. Найти э.д.с. индукции в контуре как функцию расстояния r.
Ответ: 0I lv
2 r
5.15. Квадратная рамка со стороной а и длинный прямой провод с током I находятся в одной плоскости (рис 5.4). Рамку поступательно перемещают вправо с постоянной скоростью v. Найти э.д.с. индукции в рамке как функцию расстояния х.
Ответ: |
0 |
|
I a2v |
2 |
|
x(x a) |
|
|
|
5.16. По двум гладким медным шинам, установленным под углом к горизонту, скользит под действием силы тяжести медная перемычка массы m (рис 5.5). Шины замкнуты на сопротивление R. Расстояние между шинами l. Система находится в однородном магнитном поле с индукцией В, перпендикулярном плоскости. В которой перемещается перемычка. Сопротивление шин, перемычки и скользящих контактов, а также самоиндукция контура пренебрежимо малы. Найти установившуюся скорость перемычки.
Ответ:v
mgRsin
Bl 2
b
 O
O
R  В
В
a
I
O
Рис.5.5 |
Рис.5.6 |
5.17. Квадратная проволочная рамка со стороной а и прямой проводник с постоянным током I лежат в одной плоскости (рис 5.6). Сопротивление рамки R. Ее повернули на
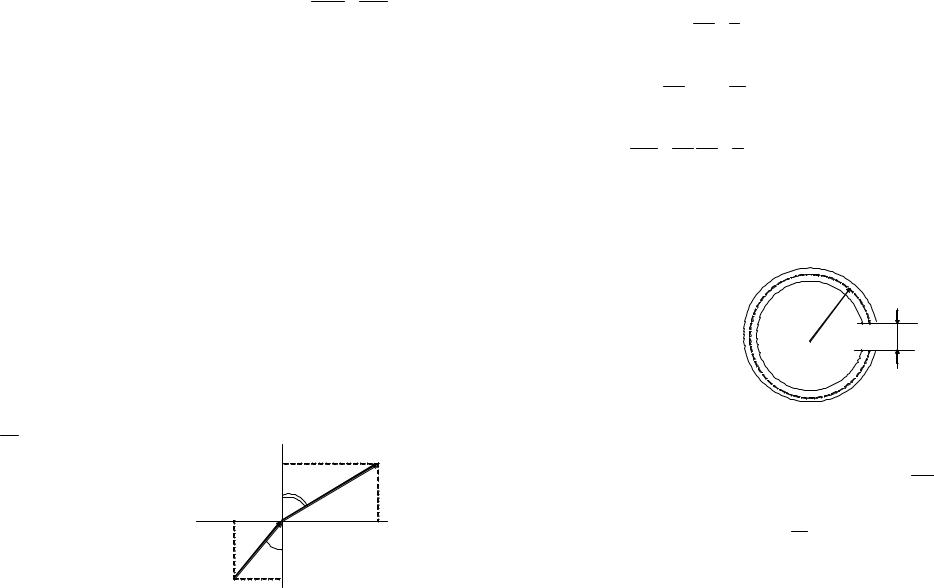
180 вокруг оси ОО, отстоящей от проводника с током на расстояние b. Найти количество электричества, протекшее в рамке.
Ответ:q 0I a ln b a
2 R |
b a |
§6. Магнитное поле в веществе.
Краткие теоретические сведения
Теорема о циркуляции вектора индукции магнитного поля:
 Bdl 0 I I / ,
Bdl 0 I I / ,
L
где I – алгебраическая сумма макротоков (токов проводимости), I/ - алгебраическая сумма микротоков (молекулярных токов), охватываемых произвольным замкнутым контуром L.
Теорема о циркуляции вектора напряженности магнитного поля:
 Нdl I ,
Нdl I ,
L
где I – токи проводимости, которые охватываются контуром L.
Циркуляция намагниченности J по произвольному замкнутому контуру L равна алгебраической сумме молекулярных токов I/, охватываемых этим контуром:
 Jdl I / .
Jdl I / .
L
Намагниченность:
J H ,
где - безразмерная величина, называемая магнитной восприимчивостью вещества. Магнитная проницаемость вещества: 1 .
B 0 H 0 1 H .
B
H J
0
II. Примеры решения задач
Пример 6.1. Индукция магнитного поля в вакууме вблизи плоской поверхности однородного изотропного материала равна В0, причем вектор В0 составляет угол 0 с нормалью к поверхности. Магнитная проницаемость материала . Найти угол , который составляет вектор В с нормалью внутри магнетика.
|
Вn |
|
В |
В0 |
|
||
|
В |
||
=1 |
|
|
|
|
В0n |
|
|
В0 |
|
|
|
0 |
|
|
|
|
|
Рис. 6.1. |
|
Решение.
Вблизи границы раздела двух сред ( 1 и2) выполняются следующие условия:
В0n Вn, В0 1
B
Из рисунка
tg 0 B0 , tg B . B0n Bn
Тогда
tg 0 B0 Bn 1 tg B B0n
tg tg 0
Пример 6.2. На железном сердечнике в виде тора со средним радиусом R имеется обмотка общим числом N витков. В сердечнике сделана поперечная прорезь шириной b. При токе I через обмотку индукция магнитного поля в зазоре равна В. Пренебрегая рассеянием магнитного потока на краях зазора, найти магнитную проницаемость железа в этих условиях.
Решение.
Теорема о циркуляции вектора напряженности
магнитного поля:
 Нdl IП ,
Нdl IП ,
L
где IП – токи проводимости, которые охватываются контуром L. Замкнутый контур выбирают вдоль силовой линии магнитного поля (H =const). Тогда
|
|
|
|
|
Н1dl Н0dl  Нdl ,
Нdl ,
L1 L0 L
b
R
 В0
В0
Рис. 6.2
где L1 – длина контура в железном сердечнике, L0 – длина контура в зазоре. H1 B0
0
- напряженность магнитного поля в железном сердечнике, - магнитная проницае-
мость железа, В0 – индукция магнитного поля в зазоре. H0 B0 - напряженность маг-
0
нитного поля в зазоре (Bn1 = Bn2 = B0). Силу тока IП можно определить как произведение количества витков, которые пересекают контур, на силу тока в одном витке I. Тогда:

H1L1 H0L0 N I, |
|
|
|
||||
B0 |
2 R b |
|
B0 |
|
b N I |
|
|
0 |
|
0 |
|
||||
|
|
|
|
|
|||
|
B0 2 R b |
|
|
2B0 R |
2 R b |
||
|
0N I B0b |
||||||
|
|
0N I B0b |
|
|
|||
Пример 6.3. Постоянный магнит имеет вид кольца с узким зазором между полюсами. Средний диаметр кольца d = 20 см. Ширина зазора b = 2 мм, индукция магнитного поля в зазоре В0 = 40 мТл. Пренебрегая рассеянием магнитного потока на краях зазора, найти модуль напряженности магнитного поля внутри магнита.
Решение.
Теорема о циркуляции вектора напряженности магнитного поля:
 Нdl IП ,
Нdl IП ,
L
где IП = 0 – токи проводимости, которые охватываются контуром L. Замкнутый контур выбирают вдоль силовой линии магнитного поля (H =const). Тогда:
|
|
|
|
Н1dl Н0dl 0,
L1 L0
где L1 – длина контура в постоянном магните, L0 – длина контура в зазоре.
Н1 d b H0b 0 .
H0 B0 - напряженность магнитного поля в зазоре, тогда:
0
Н1 |
d b |
B0b |
0, H1 |
|
|
B0b |
|
. |
|||||||||
|
|
|
0 |
d b |
|||||||||||||
|
|
|
|
|
0 |
|
|
||||||||||
Н1 |
|
40 10 3 2 10 3 |
|
|
102 |
Ам . |
|||||||||||
4 3,14 10 7 3,14 0,2 2 10 3 |
|||||||||||||||||
Н |
|
Тл м |
|
Тл А м |
|
Тл А м |
|
А |
. |
||||||||
|
|
|
|
2 |
|
||||||||||||
1 |
|
Гн |
м |
|
|
Вб |
Тл м |
|
|
|
|
||||||
|
|
|
|
|
|
м |
|
||||||||||
|
|
м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Знак «-» указывает, что Н1 и В0 антипараллельны.
III. Задачи для самостоятельного решения.
6.1. Найдите магнитную индукцию В в узкой щели, прорезанной в магнетике с проницаемостью , если магнитная индукция в окрестности щели равна В1. Щель прорезана параллельно В1.
Ответ: B B1
6.2. Найдите магнитную индукцию В в узкой щели, прорезанной в магнетике с проницаемостью , если магнитная индукция в окрестности щели равна В1. Щель прорезана перпендикулярно В1.
Ответ: B B1 6.3 Индукция магнитного поля в вакууме вблизи плоской поверхности однородного изотропного магнетика равна В0, причем вектор В0 составляет угол 0 с нормалью к поверхности. Магнитная проницаемость . Найти индукцию магнитного поля в магнетике вблизи поверхности.
Ответ: B B0 
 cos2 0 2 sin2 0
cos2 0 2 sin2 0
6.4. Прямой бесконечно длинный проводник с током лежит в плоскости раздела двух непроводящих сред с магнитными проницаемостями 1 и 2. Найти модуль вектора индукции магнитного поля во всем пространстве в зависимости от расстояния r до провода. Иметь в виду, что линии вектора В являются окружностями с центром на оси проводника.
Ответ: B I 0 1 2
r 1 2
6.5. На железном сердечнике в виде тора со средним радиусом R = 250 мм имеется обмотка общим числом N = 1000 витков. В сердечнике сделана поперечная прорезь шириной b = 1 мм. При токе I = 0,85 А через обмотку индукция магнитного поля в зазоре равна В = 0.75 Тл. Пренебрегая рассеянием магнитного потока на краях зазора, найти магнитную проницаемость железа в этих условиях.
Ответ: |
|
2 R b |
|
|
|
|
2 R |
, = 3,7 |
103. |
|
0 |
|
|
|
|
0 |
NI bB |
||||
|
|
|
|
|
||||||
|
NI bB |
|
|
|
|
|
|
|||
6.6. Железное кольцо средним диаметром |
|
0 |
|
|
|
|
|
|
|
|
d |
= 11.4 |
|
см |
|
имеет |
обмотку |
из |
|||
N = 200 витков, по которой течет ток силой I0 = 5 А. Какой ток должен протекать через обмотку, чтобы индукция в сердечнике осталась прежней, если в кольце сделать прорезь шириной b = 1 мм? ( = 3 103).
Ответ: I I0 d b 1 , I = 61 А.
d
6.7. Постоянный ток I течет вдоль длинного однородного цилиндрического провода круглого сечения. Провод сделан из парамагнетика с магнитной восприимчивостью . Найти объемный молекулярный ток.
Ответ: IМ I 6.8. Постоянный ток I течет вдоль длинного однородного цилиндрического провода круглого сечения. Провод сделан из парамагнетика с магнитной восприимчивостью . Найти поверхностный молекулярный ток.
Ответ: IМ I

§7. Колебательный контур
I. Краткие теоретические сведения
Колебательный контур – это электрическая цепь, содержащая катушку индуктивности и конденсатор, в которой могут возбуждаться электрические колебания. Свойства колебательного контура определяются его параметрами: индуктивностью, емкостью и сопротивлением.
Уравнение колебательного контура, содержащего последовательно соединенные конденсатор С , катушку индуктивности L , активное сопротивление R и внешнюю переменную э. д. с. E. Тогда уравнение колебательного контура имеет вид
|
|
|
L |
d2q |
R |
dq |
1 |
q Е |
|
||||
|
|
|
|
|
|
|
|
|
|
||||
или |
|
|
dt2 |
dt |
|
C |
|
||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
Е |
|
||
|
|
|
|
|
|
2 |
|
|
|
||||
|
|
|
q 2 q 0 q |
L , |
|
||||||||
где |
|
R |
- коэффициент затухания, |
2 |
|
1 |
|
|
– собственная частота. |
||||
|
|
0 |
|
|
|
|
|
||||||
2L |
LC |
||||||||||||
|
|
|
|
|
|
|
|
||||||
|
Если E 0 , то колебания называются свободными. При |
R 0 они будут незату- |
|||||||||||
хающими, при R 0 - затухающими. |
|
|
|
|
|
|
|
|
|||||
Уравнение свободных незатухающих колебаний представляет собой частный случай уравнения (7.1), когда E и R 0
q 02q 0,
его решение
q qm cos 0t ,
где qm - амплитудное значение заряда на обкладке конденсатора, - начальная фаза,
причем обе постоянные определяются начальными условиями. Колебания в таком контуре происходят с периодом (формула Томсона)
T 2 
 LC .
LC .
Уравнение свободных затухающих колебаний представляет собой частный случай уравнения (7.1) при E = 0
|
|
|
|
|
2 |
|
|
|
|
|
|||
решение которого имеет вид |
|
q |
2 q |
0 q 0, |
|
|
|
||||||
q qme t cos 0t , |
|
|
|
||||||||||
где |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
R |
|
2 |
|
|||
|
2 |
|
2 |
|
|||||||||
|
0 |
|
|
|
|
|
|
|
. |
||||
|
|
LC |
|
||||||||||
|
|
|
|
|
|
|
|
2L |
|
|
|||
Зная q t , можно найти напряжение на конденсаторе и ток в контуре как
UC |
|
q |
|
qm |
e t cos t Um0e t cos t , |
C |
|
||||
|
|
|
C |
||
где Um0 – начальная амплитуда,
Idq qme t cos t sin t qme t cos t , dt
где угол определяется из формул
 0 cos ,
0 cos ,  0 sin .
0 sin .
При гармонических вынужденных колебаниях в контур включена внешняя пере-
менная э. д. с. E зависящая от времени по гармоническому закону
E(t) Em cos t .
Тогда уравнение колебательного контура (7.1) принимает вид
|
|
|
|
|
|
|
2 |
|
|
E |
||||||||
|
|
|
|
|
|
cos t , |
||||||||||||
|
|
|
q 2 q 0 q |
|
||||||||||||||
Сила тока в этом случае меняется по закону: |
L |
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
I Im cos t , |
||||||||||||||
амплитудные значения силы тока и напряжения связаны законом Ома |
||||||||||||||||||
|
|
|
Im |
|
|
|
|
Um |
|
|
|
|
, |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
R2 XL XC 2 |
|||||||||||
|
XL |
|
L , |
|
XC |
|
|
1 |
, tg |
XL XC |
. |
|||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
R |
|||
Здесь XL и XC – индуктивное и емкостное сопротивления. Напряжение и ток сдви-
нуты по фазе на угол .
II. Примеры решения задач
Пример 7.1. Ток в колебательном контуре зависит от времени как I I0 sin 0t , где
Im 9 |
мА, |
0 |
4,5 104 с-1. Емкость конденсатора C 0,5 мкФ. Найти индуктивность |
||||||
контура и напряжение на конденсаторе в момент t 0 . |
|||||||||
|
|
|
|
|
Решение. |
|
|||
По |
|
условию задачи |
ток |
изменяется по закону |
|||||
I I0 sin 0t , |
т.е. в контуре (рис.6.1) происходят свободные |
||||||||
незатухающие колебания, а уравнение колебательного контура |
|||||||||
имеет вид |
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
I 0 |
, |
||
|
|
|
|
|
I |
0 |
|||
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
1 |
|
|
|||
где 0 |
|
|
|
. |
Отсюда L |
|
|
. Тогда |
|
|
|
02C |
|||||||
|
|
LC |
|
|
Рис. 6.1 |
||||

|
|
|
1 |
|
|
Idt |
|
I0 |
|
|
||||||
|
|
UC |
|
|
|
|
|
|
cos t const. |
|
|
|||||
|
|
C |
0C |
|
|
|||||||||||
Для определения постоянной, |
используем начальным условиям: при t 0 |
ток I 0 . |
||||||||||||||
Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получим |
|
|
UL LI L 0 I0 cos t , |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I0 |
UL |
|
t 0 L 0 I0 , UC |
|
t 0 0 . |
|
|
||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
||||||||||||
Откуда const |
. Подстановкой, найдем |
|
|
|||||||||||||
|
|
|
||||||||||||||
|
0C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UC |
I0 |
|
|
(1 cos t) . |
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
0C |
|
|
||||||
Пример 7.2. |
В контуре, состоящем |
из конденсатора емкости C |
и |
катушки |
||||||||||||
индуктивности |
L , совершаются свободные незатухающие колебания, |
при которых |
||||||||||||||
амплитуда напряжения на конденсаторе равна Um . Найти связь между током I в
контуре и напряжением UC на конденсаторе.
Решение.
Уравнение колебательного контура в котором происходят свободные незатухающие колебания можно записать в виде
UC LI 0.
Умножим это уравнение на UC , получим
|
|
|
q |
|
|
|
q |
UCUC LIUC 0 |
|
|
|
|
|
|
|
|
|
||
Подставляя UC |
|
и UC |
|
в последнее уравнение, имеем |
|
|
|
|
|
|
|
||||||||
C |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
C |
|
|
|
|
L I I |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
UCUC |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
C |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Интегрируя последнее уравнение, |
|||||||||
|
|
|
|
|
|
|
|
|
Ume t окончательно получим |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
UC2 |
|
L I 2 |
const Umax . |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
C |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Пример 7.3. В контуре совершаются |
|||||||||
|
|
|
|
|
|
|
|
|
|
затухающие |
свободные |
колебания, |
|||||||
|
|
|
|
|
|
|
|
|
|
при которых |
напряжение на |
||||||||
|
|
|
|
|
|
|
|
|
|
конденсаторе |
меняется |
во |
времени |
||||||
|
|
|
|
|
|
|
|
|
|
по закону U Ume t |
cos t . Найти |
||||||||
|
|
|
Рис. 7.2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
моменты |
времени, |
когда |
модуль |
||||||||
|
|
|
|
|
|
|
|
|
|
напряжения |
|
на |
конденсаторе |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
достигает:
а) амплитудных значений; б) максимальных (экстремальных) значений.
Решение.
а). Из рис.7.2 видно, что модуль напряжения на конденсаторе достигает амплитудных
t t
значений при выполнении равенства Ume cos t Ume , что возможно, если cos t 1. Таким образом,
t n, n 0, 1, 2,...
откуда
t n, n 0, 1, 2,...
б). Для нахождения максимальных значений напряжения на конденсаторе следует приравнять нулю первую производную U U t , т.о.
dUdt sin tUm e t cos tUm be t 0.
Отсюда получим, что tg t , тогда t
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
n |
|
|||
t |
n |
|
|
arctg |
|
|
|
|
, |
n 0, 1, 2,... |
|
|
|
||||||||
|
|
|
|
|
|
|
||||
|
|
n , откуда |
|
arctg |
|
|
|
|
|||
|
|
|
|
. |
|
|
|
Пример 7.4. Найти коэффициент затухания и |
|
|
|
|
|
|
|
||||||||||
частоту свободных |
затухающих |
колебаний |
|
|
|
|
|
|
|
||||||||
контура |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(см. рис. 7.3). |
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
По второму закону Кирхгофа |
|
E . |
|
|
|
|
|
|
|
|
|
||||||
UC UL |
UL |
UR |
UR |
2 |
|
|
|
|
|
|
|
|
|
||||
1 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Так как колебания свободные, то E = 0. Под- |
|
|
|
|
|
|
|
||||||||||
ставив значения напряжений, получим |
|
|
|
|
|
|
Рис. 7.3 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I dt |
|
|
|
|
|
I dt |
|
|
|
|
|
|
)I 0, |
|||
|
|
L I |
R I R I L I |
|
|
(L L |
)I (R R |
2 |
|||||||||
|
|
|
|
||||||||||||||
|
C |
1 |
1 |
2 |
|
2 |
|
|
C |
1 |
|
|
2 |
1 |
|
||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
||
|
|
|
I |
(L1 L2) I (R1 R2) |
|
|
0; |
|
|
||||||||
|
|
|
C |
|
|
||||||||||||
|
|
|
|
(R1 R2) |
|
|
I |
0. |
|
|
|||||||
|
|
|
I I |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
(L1 L2) |
(L1 L2) C |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
Откуда
2 |
(R1 R2) |
, |
2 |
|
1 |
|
|
. |
||
(L L |
|
) |
(L L |
|
|
|||||
|
2 |
|
0 |
|
2 |
) C |
||||
1 |
|
|
|
|
1 |
|
|
|||
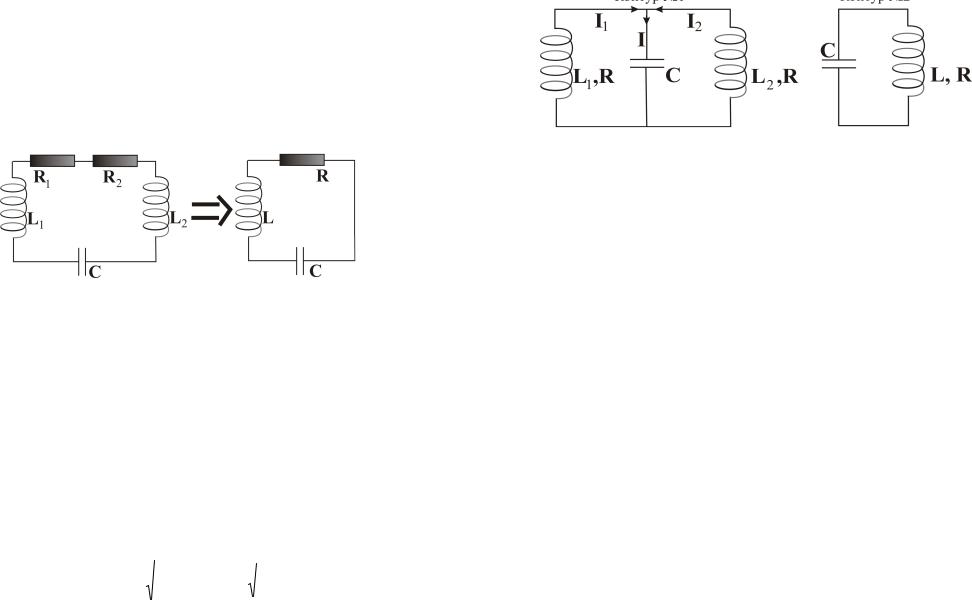
Пример 7.5. Некоторый колебательный контур содержит две последовательно соединенные катушки с активными сопротивлениями R1 , R2 и индуктивностями L1 ,
L2 , причем взаимная индуктивность пренебрежимо мала. Эти катушки нужно
заменить одной так, чтобы частота и добротность не изменялась. Найти L и R такой катушки.
Рис. 7.4 а Рис. 12.4 б
Решение.
По условию задачи схему, изображенную на рис. 7.4 а, нужно заменить эквивалентной
схемой, показанной на рис. 7.4 б. |
|
|
|
|
|
|
|
|
|
|
|
||||
Запишем |
уравнение |
колебательного |
|
контура |
|
для |
первой |
схемы |
|||||||
(рис. 7.4 а), полученное в предыдущем примере |
|
|
|
|
|
|
|||||||||
|
|
(R1 R2) |
|
|
|
I |
0 |
, |
|
|
|
||||
|
I |
I |
|
|
|
|
|
|
|
|
|
|
|||
тогда |
(L1 L2) |
(L1 L2) C |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
(R1 R2) |
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
, 2 |
|
1 |
|
|
. |
|
|
||||||
|
|
|
(L L ) |
0 |
|
(L L ) C |
|
|
|||||||
|
|
1 |
2 |
|
|
|
|
1 |
2 |
|
|
|
|
||
Собственная частота колебательного контура, изображенного на второй схеме,
равна 2 |
|
1 |
. Приравнивая частоты, |
найдем L L |
L . |
|||||||||||
|
||||||||||||||||
0 |
|
LC |
|
|
|
|
|
|
|
1 |
|
2 |
||||
Приравняв добротности, получим |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
L |
|
|
||||||
|
|
|
Q |
0 |
|
|
|
|
|
|
|
|
, |
|||
|
|
|
|
|
(R R |
|
) |
|
C |
|||||||
|
|
|
|
|
4 |
2 |
|
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||
откуда
R R1 R2 .
|
A |
|
|
|
B |
|
|
|
|
|
|
||
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 7.5
Пример 7.6. Имеются два колебательных контура (рис. 7.5). При каком соотношении между индуктивностями частоты свободных колебаний в контурах одинаковы?
Решение.
Запишем уравнения колебательного контура А, воспользовавшись первым законом Кирхгофа для замкнутых контуров L1CR и L2CR
|
|
|
|
|
|
|
R1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
I 0; |
|
|
|
|
|||||||||||||
|
|
I1 |
|
|
|
|
|
|
|
I1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
L1 |
|
|
L1 C |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I 0; |
|
|
|
||||||||||||||||||
|
|
I2 |
|
|
|
|
|
|
|
I |
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
L2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L2 C |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
R |
2 |
|
|
|
|
|
|
|
|
I |
1 |
|
|
1 |
|
|
||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|||||||||||
I |
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
, |
||||||||||
L |
|
|
|
|
L |
|
|
|
|
|
|
|
|
L |
|
L |
|||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
C |
|
|
|
|
|
|||||||||||
тогда собственная частота равна |
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
C |
|
|
L |
|
|
L |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|||||||
Уравнение колебательного контура В имеет вид |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
1 |
I RI LI 0 , |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
или |
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I 0, |
|
|
|
|
|
|
|||||||||||||
|
|
|
I |
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
L |
|
LC |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
т.е. или собственная частота равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
021 |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
LC |
|
|
|
|
|
|
|
|
|
|
|
|
||||
По условию задачи частоты свободных колебаний в контурах одинаковы
021 02 , тогда
