матан 3 курс 2013 / практика / Частинні похідні і диференціали / практичне заняття № 19

Міністерство освіти і науки України

Горлівський технікум Донецького національного університету

ПРАКТИЧНЕ ЗАНЯТТЯ № 19

з теми: «Частинні похідні та диференціали функції багатьох змінних. Геометричний зміст, похідна за напрямом.»

Модуль КЗН-02.ПР.О.03.13 Частинні похідні і диференціали

Дисципліна: «Математичний аналіз»

Розглянуто та схвалено Розробив викладач

на засіданні циклової циклової комісії ПМ

комісії «Прикладна математика». Велікодна О. В.

протокол № ____ від _______200__ р.

Голова циклової

комісії ПМ І. П. Сошина

ПЛАН ЗАНЯТТЯ

Дата: курс: ІІI

Викладач: Велікодна Ольга Володимирівна.

Тема: Частинні похідні та диференціали функції багатьох змінних. Геометричний зміст, похідна за напрямом.

Мета:

• Дидактична: виробити вміння диференціювати функції багатьох змінних – знаходити частинні похідні, дотичну площину до поверхні в заданій точці, знаходити похідну функції за наданим напрямом.

• Виховна: підвищити рівень засвоєння навчального матеріалу, розвивати наукове мислення, усне мовлення студентів.

• Методична: вдосконалювати методику проведення практичних занять з використанням технології проблемного та проектного навчання.

Тип: практичне заняття

Вид: практичне заняття – дослідження.

Методи та форми проведення заняття: практичні, дедуктивні, проблемно – пошукові, фронтальна, групова робота.

Наочні посібники: -

Роздавальний матеріал: тестові завдання до актуалізації знань, картки - завдання до самостійного виконання студентами.

Обчислювальні засоби: -

Література:

1. Кудрявцев Л.Д. Курс математического анализа: Учебник. Для студентов университетов и вузов. В 3 т. - М.: Высшая школа,1998.

2. Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989.

3. Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для вузов. - М.: Наука. Гл. ред. физ. - мат. лит.,1975.

ХІД ЗАНЯТТЯ.

1. Організаційна частина:

1. відсутні;

2. підготовка до заняття;

3. перевірка д/з.

2. Мотивація навчальної діяльності студентів:

3. Актуалізація опорних знань:

• Контроль за підготовкою студентів до практичного заняття:

4. Інструктаж щодо виконання практичної роботи.

5. Видача завдань для виконання роботи.

6. Виконання студентами практичної роботи.

7. Оформлення індивідуальних звітів виконаної роботи, захист практичної роботи.

8. Підведення підсумків. Оцінювання.

9. Домашнє завдання:

Конспект практичного заняття № 19.

Тема: «Частинні похідні та диференціали функції багатьох змінних. Геометричний зміст, похідна за напрямом.»

Інструктаж щодо виконання практичного завдання.

Нехай функція визначена в деякім околі точки . Тоді , наприклад, частинною похідною в точці називається звичайна похідна в точці функції, отримана з даної фіксуванням всіх аргументів, окрім першого.

Нехай , тоді - приріст функції в точці по змінній . Далі, користуючись визначенням похідної отримаємо: .

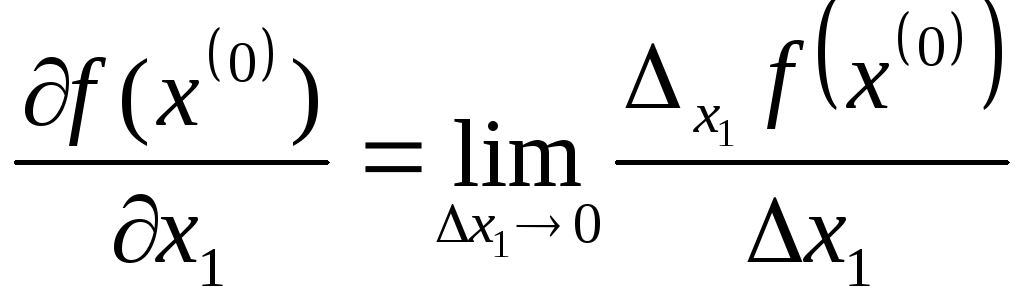Аналогічно визначаються похідні функції по іншим змінним. Існування у функції всіх частинних похідних в точці не означає неперервність функції в цій точці.

Визначення. Функція z = ƒ(х, у) називається диференційованою в точці , якщо існують два числа А та В, що .

Якщо функція z = ƒ(х, у) диференційована в точці , то лінійна функція змінних називається диференціалом функції в точці та позначається dz: .

Теорема 1. Якщо функція диференційована в деякій точці, то вона неперервна в цій точці.

Теорема 2. Якщо функція z = ƒ(х, у) диференційована в точці та - її диференціал в цій точці, то у функції ƒ в точці існують частинні похідні по х та по у, причому . Таким чином, диференціал можна записати у вигляді .

Теорема 3. Якщо функція має в околі точки частинні похідні та вони неперервні в цій точці, то функція диференційована в ній.

Розглянемо композицію функції двох змінних та функції однієї змінної.

Теорема 4. Якщо функції х = х(t) та у = у(t) диференційовані в точці , а функція z = ƒ(х, у) диференційована в точці , де , то складна функція диференційована в точці та в цій точці .

Якщо функції х = х(u, v) та у = у(u, v) диференційовані в точці та мають в цій точці частинні похідні , а функція z = ƒ(х, у) диференційована в точці , де , то в точці існують частинні похідні складної функції z = ƒ(х(u, v), у(u, v)) та , .

Запис диференціалу функції багатьох змінних має один й той самий вигляд як відносно незалежних, так і відносно залежних змінних.

Теорема 5. Якщо функції хі = хі(t), і =1,…, n мають в точці неперервні частинні похідні, а функція у = ƒ(х) – неперервні частинні похідні в точці , де , то складна функція ƒ(х(t)) диференційована в точці та - інваріантність форми першого диференціалу.

Розглянемо функцію двох змінних z = ƒ(х, у). Нехай в точці функція має частинну похідну , де α за геометричним змістом похідної функції однієї змінної є кутом нахилу дотичної до графіку цієї функції, тобто до кривої z = ƒ(х, у), у = у0, в точці (х0, у0, z0), де z0 = ƒ(х0, у0). В цьому й є зміст частинної похідної.

Площина, що визначається рівнянням називається дотичною площиною до графіку функції z = ƒ(х, у) в точці (х0, у0, z0). Якщо аплікату дотикання позначити z0, то , z = ƒ(х, у). Також, . Таким чином, диференціал функції дорівнює приросту аплікати дотичної площини до графіку функції.

Нехай функція ƒ(х, у, z) визначено в околі точки (х0, у0, z0) та заданий вектор l, l ≠ 0. Позначимо через його напрямні косинуси, тобто координати одиничного вектору . Розглянемо композицію функцій ƒ(х, у, z) та , тобто . Права похідна цієї функції в точці t=0 називається похідною функції ƒ(х, у, z) в точці (х0, у0, z0) за напрямом вектору l, та позначається .

Користуючись формулою диференціювання складної функції, отримаємо , де . Далі будемо мати: - похідна функції ƒ(х, у, z) в точці (х0, у0, z0) за напрямом вектору l.

Вектор називається градієнтом функції ƒ(х, у, z) та позначається . Градієнт функції не залежить від вибору системи координат, якщо , то напрямок градієнту є єдиним напрямом, за яким похідна за напрямом в даній точці має найбільше значення, а довжина градієнту дорівнює цьому найбільшому значенню. Якщо ж , то в даній точці похідні за всіма напрямами дорівнюють нулю.

Завдання для студентів.

Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. – Том 3. - М.: Наука. Гл. ред. физ. - мат. лит.,1989.

Стор. 65, № 1 – 3, стор. 66, № 13, стор. 68, № 21, стор. 71, № 39, стор. 72, № 48.