матан 3 курс 2013 / практика / Визначений інтеграл / практическое занятие № 9

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ГОРЛІВСЬКИЙ ТЕХНІКУМ ДОНЕЦЬКОГО НАЦІОНАЛЬНОГО УНІВЕРСИТЕТУ

ПРАКТИЧНЕ ЗАНЯТТЯ № 9

з теми: «Геометричний та фізичний зміст визначеного інтеграла.»

Модуль КЗН-02. ПР.О.03.08 Визначений інтеграл

Дисципліна: «Математичний аналіз»

Розглянуто та схвалено на засіданні циклової комісії інформаційних технологій та прикладної математики протокол № ____ від _______20__ р. Голова циклової комісії ПМ О.В. Велікодна

Розробив викладач Велікодна О. В.

ПЛАН ЗАНЯТТЯ

Дата: курс: ІІI

Викладач: Велікодна Ольга Володимирівна.

Тема: Геометричний та фізичний зміст визначеного інтеграла.

Мета:

• Дидактична: поглибити навички застосування таблиці первісних для знаходження інтеграла Ньютона – Лейбніца, розвивати вміння володіти методами інтегрування, досліджувати функцію на інтегрованість за Ріманом, застосовувати інтеграл Рімана при розв'язанні задач геометрії, механіки та фізики.

• Виховна: підвищити рівень засвоєння навчального матеріалу, розвивати наукове мислення, усне мовлення студентів.

• Методична: вдосконалювати методику проведення практичних занять з використанням технології проблемного та проектного навчання.

Тип: практичне заняття

Вид: практичне заняття – дослідження.

Методи та форми проведення заняття: практичні, дедуктивні, проблемно – пошукові, фронтальна, групова робота.

Наочні посібники: -

Роздавальний матеріал: тестові завдання до актуалізації знань, картки - завдання до самостійного виконання студентами.

Обчислювальні засоби: -

Література:

1. Кудрявцев Л.Д. Курс математического анализа: Учебник. Для студентов университетов и вузов. В 3 т. - М.: Высшая школа,1998.

2. Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989.

3. Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для вузов. - М.: Наука. Гл. ред. физ. - мат. лит.,1975.

4. Марон А. И. Дифференциальное и интегральное исчисление функции одной переменной в примерах и задачах. – М.: Наука, 1973.

ХІД ЗАНЯТТЯ

1. Організаційна частина:

1. відсутні;

2. підготовка до заняття;

3. перевірка д/з.

2. Мотивація навчальної діяльності студентів: вивчити основний математичний апарат – невизначений інтеграл, що дає змогу розв’язувати прикладні задачі в різних галузях науки та техніки.

3. Актуалізація опорних знань: задача про знаходження площі криволінійної трапеції в полярних та декартових координатах, задача про знаходження довжини кривої, задача про знаходження площі поверхні та об’єму поверхні обертання; фізичні застосування визначеного інтегралу.

• Контроль за підготовкою студентів до практичного заняття:

4. Інструктаж щодо виконання практичної роботи.

5. Видача завдань для виконання роботи.

6. Виконання студентами практичної роботи.

7. Оформлення індивідуальних звітів виконаної роботи, захист практичної роботи.

8. Підведення підсумків. Оцінювання.

9. Домашнє завдання:

Конспект практичного заняття № 9.

Тема: «Геометричний та фізичний зміст визначеного інтеграла.»

1. Інструктаж до виконання практичного завдання.

Методичні вказівки.

Геометричний зміст.

Якщо функція ƒ невід’ємна та неперервна на відрізку [a, b], а множина Р = {(х, у):

a ≤ х ≤ b, 0 ≤ у ≤ ƒ(х)}, то площа множини Р виражається формулою S = .

Множина Р = {(х, у): a ≤ х ≤ b, 0 ≤ у ≤ ƒ(х)} називається криволінійною трапецією, що породжена графіком функції ƒ.

Якщо функція ƒ не додатна та неперервна на відрізку [a, b], а множина Р= {(х, у): a ≤ х ≤ b, ƒ(х) ≤ у ≤ 0}, то площа множини Р виражається формулою S = -.

Нехай Р – замкнена множина, границя якого складається з деякої кривої, що задана в полярних координатах ρ = ρ(φ), α ≤ φ ≤ β, ρ(φ) – неперервна функція, та двох відрізків промінів φ = α, φ = β. Тоді площа множини Р дорівнює інтегралу S = .

Нехай Г – крива, що задана своїм неперервно диференційованим векторним представленням r = r(t), a ≤ t ≤ b. За формулою Ньютона - Лейбніца для довжини S кривої маємо формулу: S = . Якщо r(t) = {х(t), у(t), z(t)}, то

S = .

У випадку, коли крива Г є графіком функції у = ƒ(х), a ≤ х ≤ b, для її довжини S справедлива формула S = .

Нехай функція ƒ невід’ємна на відрізку [a, b], де a < b .Для функції у = ƒ(х) площа поверхні обертання, що обмежена функцією у, навколо осі ОХ має вид:

L = .

Якщо крива задана параметрично у виді х = х(t), у = у(t) , a ≤ t ≤ b, та не перетинає ось ОХ, то площа поверхні обертання навколо осі ОХ має вид:

L = .

Нехай функція ƒ невід’ємна та неперервна на відрізку [a, b], а Q – тіло, що отримане обертанням криволінійної трапеції Р, породженої графіком функції у = ƒ(х). Тоді об'єм V цього тіла знаходиться за формулою:

V = .

Фізичний зміст.

Нехай матеріальна точка рухається зі швидкістю v=ƒ(t) в одному напрямку, де t – час руху. Шлях s, пройдений точкою з моменту часу t = T1 до моменту часу t = T2 визначається за формулою: .

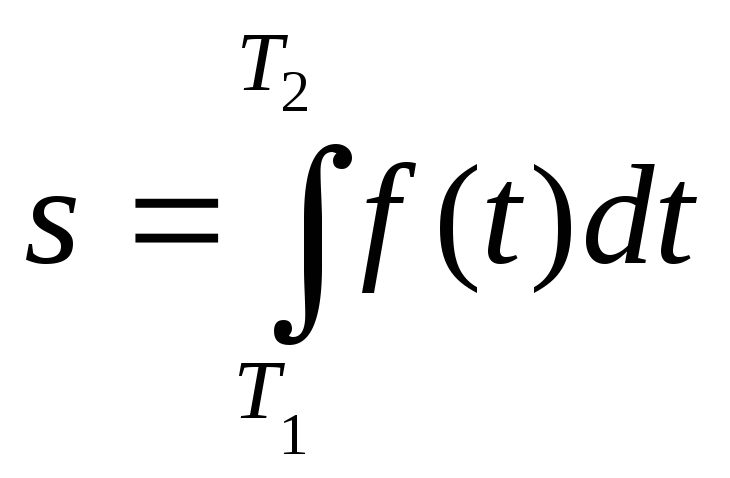Якщо стала сила F діє на матеріальну точку, що рухається за напрямом сили, то робота сили на дільниці (s1, s2) знаходиться за формулою A = Р(s2 - s1). Якщо ж сила Р зберігає напрям шляху руху, але її величина змінюється в залежності від шляху s, то робота знаходиться за формулою: А = .

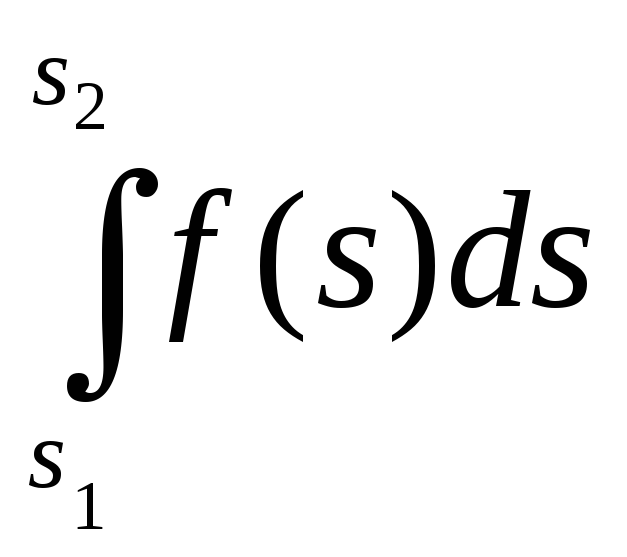Приклади виконання практичного завдання.

1. Знайти площу фігури, обмеженої параболою у = (х - 1)² та гіперболою х² - у²/2 = 1.

Розв’язання:

Знайдемо точки перетину параболи та гіперболи, розв’язавши сумісно рівняння цих кривих. Маємо: Тобто, криві перетинаються в точках А(1, 0) та В(3, 4). Тоді, площа криволінійної трапеції буде: =

= (кв. од.).

2. Знайти площу фігури, обмеженої лінією 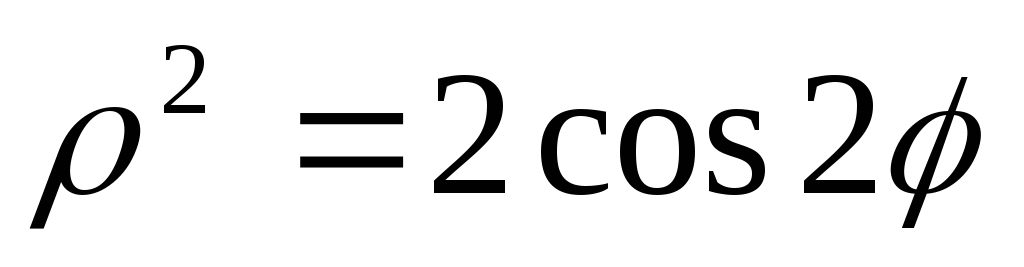(лемніската Бернуллі).

Розв’язання:

(кв. од.).

3. Знайти об'єм тіла обертання, що отримано обертанням навколо осі ОХ фігури, обмеженої лінією 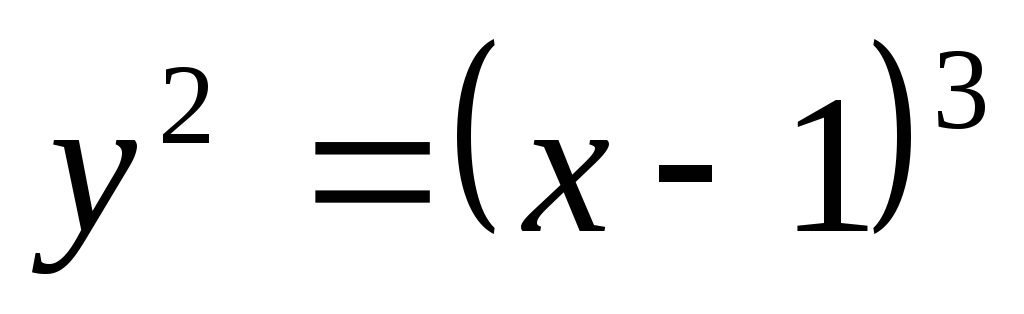та прямою х = 2.

Розв’язання:

(куб. од.).

4. Електричний ланцюг має сопротивлення R та коефіцієнт самоіндукції L. В начальний момент електрика в ланцюзі відсутня. В ланцюг подається зовнішня напруга 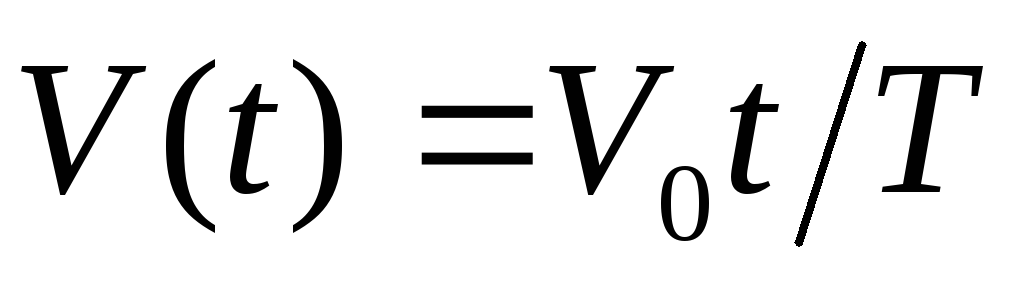, де 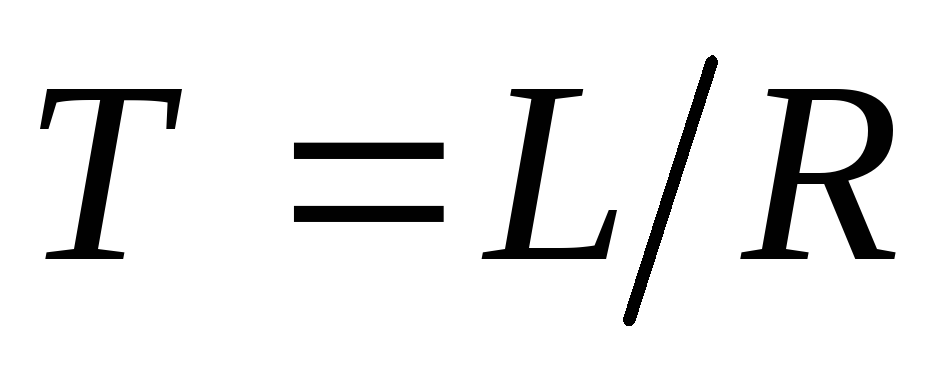. Знайти залежність І(t) току в ланцюзі від часу.

Розв’язання:

тік І(t) та швидкість його змінення зв’язані рівнянням: , з якого слідує, що . Помножимо обидві частини рівняння на , отримаємо, що ліва частина є похідна добутку . Тому маємо: . Звідки

Інтегруючи обидві частини, маємо .

Виконати практичне завдання.

Знайти площу фігури, обмеженої кривими.

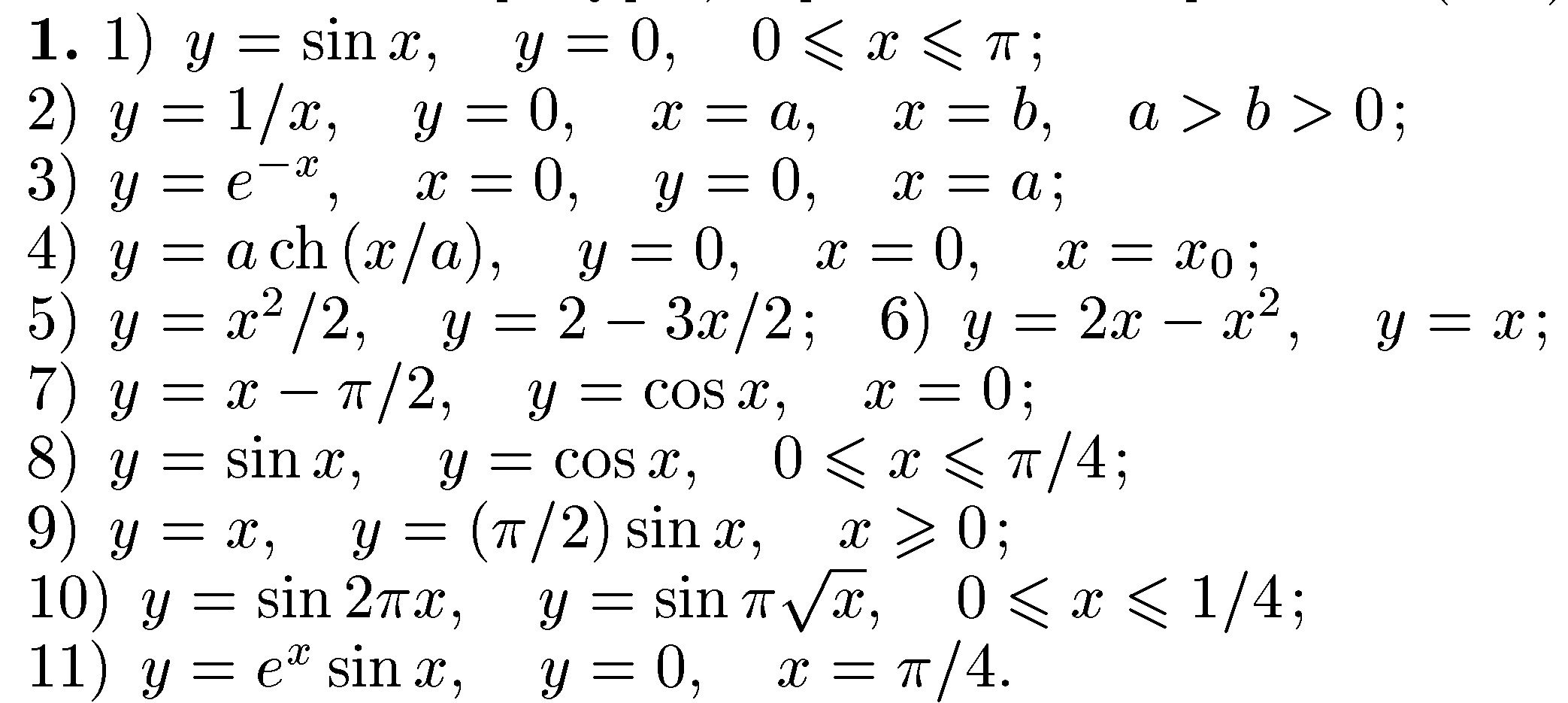
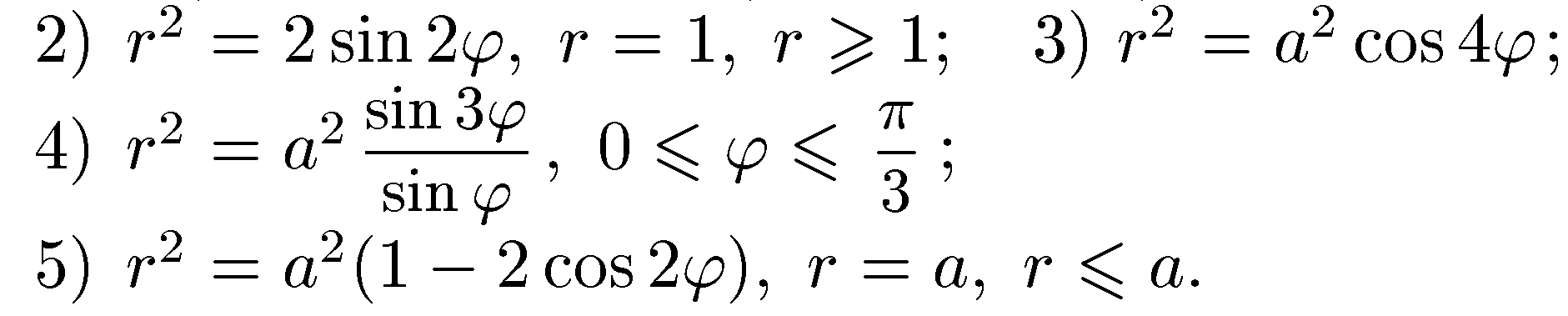
Знайти довжину дуги кривої.

Знайти об'єм тіла, що утворилось обертанням навколо осі ОХ площі, обмеженої кривими.

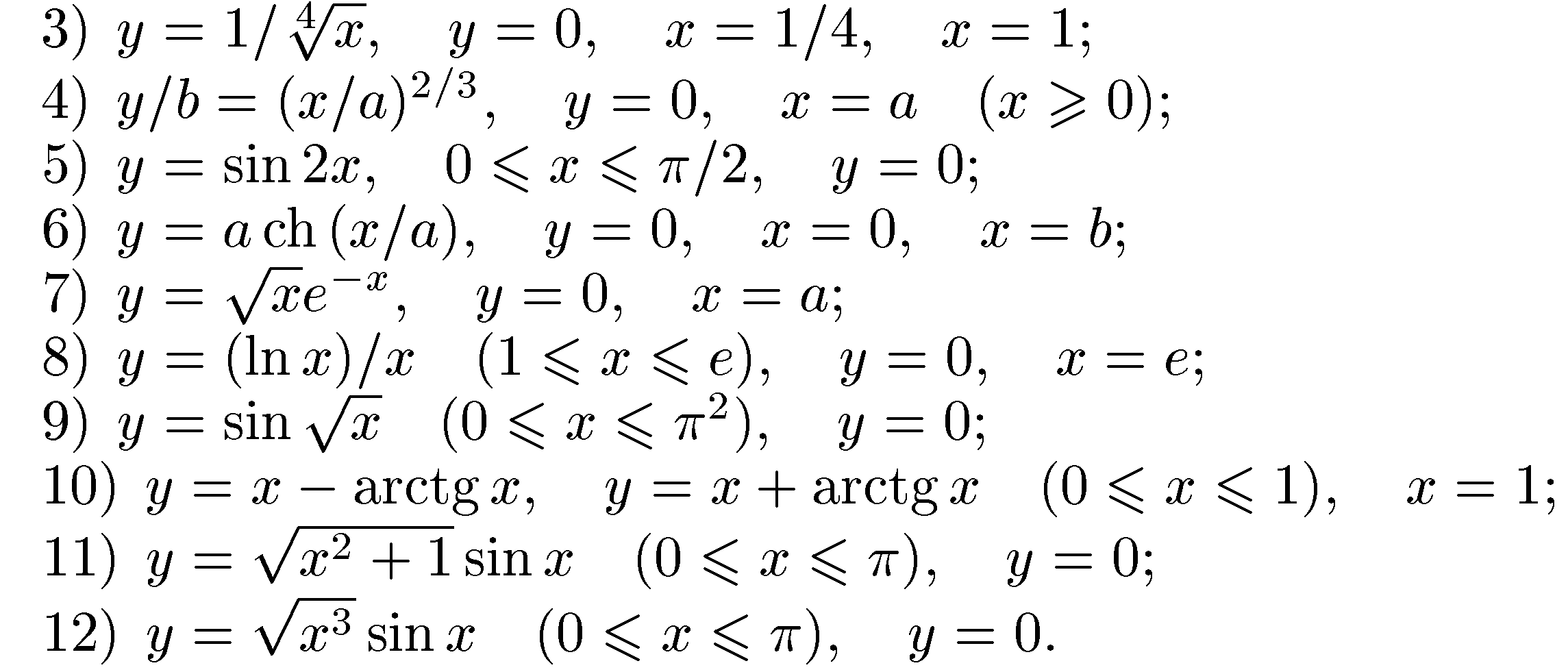
Домашнє завдання. П. Е. Данко. Высшая математика в упражнениях и задачах. Ч. 1. Стор. 253, №№1569 – 1609. Стор. 256, №№1628 – 1632.

Стор. 265 – 266, №№1670 – 1681.